当前位置：文档之家 › 4.1-数学期望PPT课件

4.1-数学期望PPT课件

  • 格式：ppt
  • 大小：409.00 KB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

《数学期望》课件

《数学期望》课件
注意事项
在计算过程中需要注意积分的上下 限以及概率密度函数的取值范围。
连续型随机变量的数学期望的性质
01
02
03
非负性
E(X) ≥ 0，即数学期望的 值总是非负的。
可加性
如果X和Y是两个独立的随 机变量，那么E(X+Y) = E(X) + E(Y)。
线性性质
如果a和b是常数，那么 E(aX+b) = aE(X)+b。
方差是数学期望的度量，表示随机变量取值 与数学期望的偏离程度。
04
CATALOGUE
连续型随机变量的数学期望
连续型随机变量的定义
连续型随机变量
如果一个随机变量X的所有可能 取值是实数轴上的一个区间变量。
概率密度函数
描述连续型随机变量X在各个点 上取值的概率分布情况，其数学
《数学期望》PPT课件
CATALOGUE
目 录
• 引言 • 数学期望的基本性质 • 离散型随机变量的数学期望 • 连续型随机变量的数学期望 • 数学期望的应用 • 总结与展望
01
CATALOGUE
引言
数学期望的定义
数学期望是概率论和统计学中的 一个重要概念，它表示随机变量
取值的平均数或加权平均数。
数学期望的定义基于概率论的基 本原理，通过将每个可能的结果 与其对应的概率相乘，然后将这
些乘积相加得到。
数学期望具有一些重要的性质， 如线性性质、期望值不变性质等 ，这些性质在概率论和统计学中
有着广泛的应用。
数学期望的起源和历史
数学期望的起源可以追溯到17世纪，当时的一些数学家开始研究概率论和统计学中 的一些基本概念。
通过计算投资组合的数学期望， 我们可以了解投资组合的预期收 益，从而制定更加合理的投资策

《数学期望》课件

《数学期望》课件
《数学期望》PPT课件
欢迎来到《数学期望》PPT课件。从定义到应用，本课程将为您全面介绍数学 期望的相关知识。
什么是数学期望
1 定义
数学期望是随机变量取值的加权平均数，是 一个平均性的数值特征。
2 意义
数学期望能够用来描述随机变量的中心位置， 是概率分布的重要特征之一。
离散型随机变量的期望
1
期望的运算规律
期望的运算规律
期望也具有线性性、单调性和保号性等运算规律， 但概率密度函数的图像更难以直观展示。
期望的性质
期望的线性性质
期望具有加法和数乘的线性运算规律，对于相互独 立的随机变量，期望还满足可加性。
期望的矩估计
期望的矩估计可以帮助我们了解随机变量的高阶特 征，如方差、偏度和峰度等。
应用实例
期望在概率分布中的应用
量的期望
离散型随机变量的期望等于随机变量取
每个值的概率乘以该值的加权和，连续
型随机变量的期望等于其概率密度函数
3
期望的运算规律和性质
的加权积分。
期望具有线性性、单调性和保号性等运
算规律，还具有可加性和矩估计等特性。
应用实例
4
期望在概率分布中和随机变量期望在实 际问题中都有广泛应用。
参考资料
• 离散数学 • 概率论与数理统计 • 数理统计方法及其应用
2
期望具有线性性、单调性和保号性等运
算规律。
3
离散型随机变量的期望定义
离散型随机变量的期望等于随机变量取 每个值的概率乘以该值的加权和。
概率分布的图像
概率分布的图像能够直观地展示数学期 望的定义和特性。
连续型随机变量的期望
连续型随机变量的期望定义
连续型随机变量的期望等于其概率密度函数的加权 积分。

4-1随机变量的数学期望18页PPT

4-1随机变量的数学期望18页PPT

(1)若离散型随机变量X的分布律为 P{ X
xk}
pk
(k 1, 2, ), 且数项级数 g(xk ) pk 绝对收敛,则
k 1
E(Y) E[g(X )] g(xk ) pk.
k 1
(2)若连续型随机变量X的概率密度为f(x), 且积分
g (x) f (x)dx 绝对收敛, 则
E (Y ) E[ g ( X )] g ( x) f ( x)dx.
xf (x, y)dxdy,
E(Y )
yfY ( y)dy
yf (x, y)dxdy.
返回 上页 下页 结束
例4 随机变量X的分布律为
X
1 0 2 3
p 1/8 1/4 3/8 1/4
求 E ( X 2 ), E (2 X 1).
解 由定理1可知
E ( X 2 ) (1)2 1 02 1 22 3 32 1 31.
1
e
x
/
,
x 0,
于是
0, x 0,
E ( X )
xf (x)dx 1
xex/ dx
xd
e x /
0
0
xe
x
/
0
0
e
x
/
d
x
ex/
0
.
返回 上页 下页 结束
二. 随机变量函数的数学期望
定理1设Y是随机变量X的函数:Y=g(X), 其中g(x)
是一元连续函数.
返回 上页 下页 结束
显然商场在该日搞促销活动预期获得的经济效益X
是一个随机变量，其概率分布为
P { X x 1 } P { X 1 2 } 0 .6 p 1 ,

41数学期望-PPT课件

41数学期望-PPT课件

1 3
四.二维随机变量函数的数学期望
Z g X , Y 如果 X,Y 是二维随机变量， 是关
于X 和Y 的二元函数，则同样可定义随机变量
Z 的数学期望如下：
( 1 ) cr ( X , Y ) 已知 { p }, ij
的数学期望为 g X , Y 则 Z
E Z E g X , Y g x , y p . i j ij
Y X
0
1
2
. 04 0 . 24 0 . 12 0 0 . 06 0 . 36 0 . 18 1 0 求 ( 1 ) E ( 2 X Y ); ( 2 ) E ( XY )
1 )E (2XY) 0 ; 解： ( (2 )E (XY ) 0 .72
例6
设随机变量 X,Y 的联合概率密度为
x
1 1 E f x ,y dxdy . xy XY x 3 3 dx dy 1 4 3 1 5 xy x2
例7
设随机变量 X,Y的联合概率密度为
6 xy , 0 x 1 , 0 y 2 1 x ， f x ,y 0 其它。 ,
2
的泊松分布，试
计算 Y X 的数学期望。 解 已知 X 的分布律为：
P X k e ,
k
从而 E Y E X k
2 2
k !
k 0 , 1 , 2 , 0 ,

k
k
k 1

e k1 !

k 0 k
则所求数学期望为

x 2 2
2
,x , ,

4.1 数学期望51页PPT

4.1 数学期望51页PPT
X 0 1 2 3 4567 pk 0.0020.0010.0020.0050.020.04 0.180.37
8 9 10 0.25 0.12 0.01 试求 X的数学E期 (X)望 .
解 E(X)00.00210.00120.002 30.00540.0250.04 60.1870.3780.25 90.121 00.017.15(分)
一、数学期望的概念
引例1 射击问题 设某射击手在同样的条
件下, 瞄准靶子相继射击90次 (命中的环数是一个随机变量). 射中次数记录如下
命中环数 k 012345
命中次数nk 2 13 15 10 20 30
频率 nk n
2 13 15 10 20 30 90 90 90 90 90 90
试问: 该射手每次射击平均命中靶多少环?
加权平均, 与一般的平均值不同, 它从本质上体 现了随机变量 X 取可能值的真正的平均值 , 也 称均值.
(2) 级数的绝对收敛性保证了级数的和不 随级数各项次序的改变而改变 , 之所以这样要
求是因为数学期望是反映随机变量X 取可能值 的平均值, 它不应随可能值的排列次序而改变.
假设
X1 2 p 0 .02 0 .98
解
射中靶的总环数 平均射中环数 射击次数
0 2 1 1 2 3 1 3 5 1 4 0 2 5 0 30 90
02113215310420 90 90 90 90 90
530 90
5 k nk 3.3.7
k0 n 设射手命中的环数为随机变量 Y .
平均射中环数 5 k nk
这些人的化验反应是相互独立的. 试说明p当 较小 时, 选取适当的k, 按第二种方法可以减少化验的次 数. 并说明 k取什么值时最.适宜 解 各人的血呈阴概 性率 反q为 应 1的 p, 因而 k个人的混合血应 呈的 阴概 性 q率 k,反 k为 个 人的混合血呈阳 的性 概反 率1应 为qk.

4-1数学期望 ppt课件

4-1数学期望 ppt课件

若级数 xk pk 绝对收敛，则称此级数的和为随 i 1
机变量 X 的数学期望。记作 :EX.

既有 EX xk pk i 1
数学期望简称期望，又称均值.
PPT课件
4
数学期望
例1 甲、乙两人射击，他们射击水平由下表给出：
X:甲击中的环数
Y:乙击中的环数
X
8
9 10
Y
P
0.1 0.3 0.6

5

1 ex 0
4 e x
EM xfM (x)dx
x0 x0
0 x 5 1 ex 4 exdx
137 1
160
PPT课件
10
数学期望
2. 令：N=min{X1, X2, X3, X4, X5}, X1, X2, X3, X4, X5是 独立同分布的,于是 利用第三章第五节P99;5.8式
P
试问哪一个人的射击水平高?
解:甲、乙的平均环数为:
8
9
10
0.2 0.5 0.3
EX 8 0.1 9 0.3 10 0.6 9.5
EY 8 0.2 9 0.5 10 0.3 9.1
甲的射击水平比乙的高.
从平均环数上看
PPT课件
5
数学期望
2. 连续型
第四章 随机变量的数字特征
§1 数学期望 §2 方差 §3 协方差及相关系数 §4 矩
PPT课件
1
数学期望
§4.1 数学期望
数学期望的概念
随机变量函数的数学期望
数学期望的性质
PPT课件
2
数学期望
例1： 某班有N人参加 考试，其中有ni个人为ai ,i=1,2,…

[工学]41-数学期望PPT课件

[工学]41-数学期望PPT课件

先确定g(X)的分布
E[g(X)]=?
电子科技大学
数学期望
定理4.1.1* 设 Y 是随机变量X的函数Y=g(X),
g(x)为连续函数
本章核心定理
1) X 是离散型随机变量，分布律为
P {X x i}p i, i 1 ,2 ,3 ....
若： g(xi)pi 绝对收 则敛 有，
i1
E(Y)E [g(X) ] g(xi)pi i1
电子科技大学
数学期望
2) X是连续型随机变量, 其概率密度为fX (x).
若 g (x )f(x ) 则
E (Y )E g (X ) g (x )fX (x )dx
例 4.1.1
例 4.1.2
例 4.1.3
思考 如何将定理推广到二维甚至更多维 的情况？
电子科技大学
数学期望
定理4.1.2. 设 ( X, Y ) 是二维随机变量, 如 果 Z = G( X, Y ) 也是同类型随机变量并且数 学期望存在, 则有
(1) 当( X, Y ) 是离散型随机变量时
E(Z) G(xi,yj)pij i1j1
(2) 当( X, Y ) 是连续型随机变量时
E (Z ) G (x ,y )f(x ,y )dxdy 电子科技大学
数学期望
例 4.1.4
例 4.1.5
例 4.1.6
练习 设随机 X与 变 Y相 量互,独 且 X立 ,Y
~N(0,1 2),则 E (X Y )
解答
三. 随机变量的数学期望的性质 设 X , X1, X2 , … , Xn 是随机变量，c, b 是常数 1）E( c ) = c;
电子科技大学
数学期望
2）E( c X) = cE(X);

4-1数学期望

4-1数学期望
解
x 1 x 1
求数学期望。
E( X )
1


xf ( x)dx
1
x 0 dx x
1
1
1 x2
dx

1
x 0 dx
0
几个重要的连续型 r.v.的期望 1) 均匀分布 U(a , b) (P83,例3)
1 , a x b, f ( x) b a 0, 其它, b 1 ab E( X ) x dx ; a ba 2
定理 1：一维情形 设 Y g( X ) 是随机变量 X的函数,
X为离散型 P{ X xk } pk , k 1, 2,
E (Y ) E[ g( X )] g( xk ) pk
k 1

X为连续型 概率密度为
f ( x)
g( x ) f ( x )dx
E (Y ) E[ g( X )]
i 1 i 1 n n
请注意: 由E(XY)=E(X)E(Y) 不一定能推出X,Y 独立
4. 设X、Y 相互独立，则 E(XY)=E(X)E(Y);
推广 :
E [ X i ] E ( X i ) (诸Xi相互独立时)
i 1 i 1
n
n
五、数学期望性质的应用
例7 解 若X~b(n,p), 求E(X) (P87,例8) X表示n重贝努利试验中事件A发生的 次数. i=1,2，…，n
盈利额 X 1
（万元）
50 0.15
30
0.6 适销 36 0.6
-- 20
0. 25 滞销 -- 40 0. 3
概率 乙企业:
产品
盈利额 X 2

概率论与数理统计-数学期望_图文

概率论与数理统计-数学期望_图文

因每个球落入每个盒子是等可能的均为1/M, 所以，对第i 个盒子，一个球不落入这个盒子 内的概率为(1-1/M)。故N个球都不落入这个 盒子内的概率为(1-1/M)n ，即
最常用的数字特征是：期望和方差。
第四章 数字特征
§4.1 数学期望
4.1.1 离散型随机变量的数学期望 概念引入：
某车间对工人生产情况进行考察，车工 小张每天生产的废品数 X 是一个随机变量 。如何定义 X 的平均值？
若统计了100天小张生产产品的情况，发现 ： 32天没有出废品；30天每天出一件废品； 17天每天出两件废品；21天每天出三件废品。
可以得到这n天中，每天的平均废品数为
这是以频率为 权的加权平均
由频率与概率的关系，
不难想到：求废品数X的平 均值时，用概率替代频率， 得平均值为：
这样，就得到一个确定的数
这是以概率为 权的加权平均
——随机变量X的期望(均值) 。
定义1: 设X是离散型随机变量, 概率分布为 P{X=xk}=pk , k=1,2, …。
解：设组织货源 t 吨。显然，应要求
2000≤t ≤4000。国家收益Y(单位:万元)是X
的函数Y=g(X)。表达式为
由已知条件, 知X的概率密度函为
可算得当 t = 3500 时， E(Y)=-2t2 + 14000t-8000000
达到最大值 1.55×106。 因此，应组织3500吨货源。
概率论与数理统计-数学期望_图文.ppt
前面讨论了随机变量及其分布。 如果我 们知道了随机变量 X 的概率分布，那么，关 于 X 的全部概率特征也就知道了。
然而，在实际问题中，概率分布是较难 确定的。且有时在实际应用中，我们并不需 要知道随机变量的所有性质，只要知道其一 些数字特征就够了。

课件：数学期望

课件：数学期望

2 0.3 0.1
求 Z1 XY2 , Z2 X Y的数学期望．
解 的取值及对应的概率如下表:
(X,Y) (1,1) (1,2) (2.1) (2,2)
XY2 1
4
28
X+Y 2 3
34
pk 0.4 0.3 0.2 0.1
E(Z1) E(XY2) 10.4 40.3 20.2 80.1 2.8 E(Z2) E(X Y) 20.4 30.3 30.2 40.1 2.7
k!
E(X) k k e k!
e
k0
k 1
k 1
(k 1)!
e e
例13. 设某种疾病的发病率为1%，在1000个人中普 查这种疾病,为此要化验每个人的血.方法是，每100 个人一组,把从100个人抽来的血混在一起化验，如 果混合血样呈阴性，则通过；如果混合血样呈阳性， 则再分别化验该组每个人的血样.求平均化验次数.
E( X Y ) 1 1 x y 6x2 y dx dy 00
( x y)6x2 ydxdy ( x y)6x2 y dxdy
P{1 X 2} 2 1 ex 10 d x e0.1 e0.2 0.0861, 1 10
P{2 X 3} 3 1 e x 10 d x e0.2 e0.3 0.0779, 2 10
P{ X 3} 1 ex 10 d x e0.3 0.7408. 3 10
因而一台收费 Y 的分布律为
引例：设随机变量X的分布律为
X -1 0 1
pk
1 3
1 3
1 3
求随机变量Y=X2的数学期望
解: Y 0 1
pk
1 3
2 3
E(Y ) 1 2 0 1 2 3 33

数学期望课件

数学期望课件
le lx , f ( x) 0, x0 , 其它
lx
E ( X ) xf ( x)dx



0
lxe
dx
1

0
xdelx
[ xe
《概率统计》
lx 0
|
e
0

lx
dx ] e
0

lx
dx
l
.
下页 结束
第四章 随机变量的数字特征
何谓随机变量的数字特征？ 通常是指与随机变量有关的，虽然不能完整地 刻划随机变量，但却能较为集中地反映随机变量某 些方面的重要特征的一些数值.
1. 数学期望的概念及性质
2. 方差的概念及性质 3. 常见分布的数字特征 4. 协方差、相关系数的概念及性质
《概率统计》 返回 下页 结束
E (Z ) E[ g ( X , Y )]
特别 E ( X )






g ( x, y) f ( x, y)dxdy .

xf ( x, y)dxdy ; E (Y )

yf ( x, y)dxdy.
y
例8．设二维随机向量(X,Y)的概率密度为
§4.1 数学期望
一、离散型随机变量的数学期望 引例．有甲、乙两射手各射击100次，他们的射击技术用 下表给出：
击中环数 次 数 频 率 击中环数 次 数 频 率 8 30 0.3 8 20 0.2 甲射手射击情况 9 10 0.1 乙射手射击情况 9 50 0.5 10 60 0.6 10 30 0.3
E ( X ) xk pk .
k 1

第四章-随机变量的数字特征PPT课件

第四章-随机变量的数字特征PPT课件

k 1
k 1
变量X的数学期望，记为E(X),即
EX xk pk k1
§4.1 数学期望
关于定义的几点说明 (1) E(X)是一个实数,而非变量,它是一种加权平均,与
一般的算术平均值不同 , 它从本质上体现了随机变量 X 取可能值的真正的平均值, 也称均值.
(2) 级数的绝对收敛性保证了级数的和不随级数各 项次序的改变而改变 , 之所以这样要求是因为数学期望 是反映随机变量X 取可能值的平均值,它不应随可能值的 排列次序而改变.
❖ 例3：设 X(),求 E (X)。
解 ： X 的 分 布 律 为 ： P ( X k ) k e k 0 , 1 , 0 k ! X的 数 学 期 望 为 ：
E(X) k ke
k0 k!
e
k1
k1
(k 1)!
ee
即E(X)
§4.1 数学期望
三、连续型随机变量的数学期望
设连续型随机变量X 的概率密度为f ( x), 若积分
§4.2 方差
(2) 利用公式计算
D (X ) E (X 2 ) [E (X )2 .] 证明 D (X ) E {X [ E (X )2 } ]
E { X 2 2 X ( X ) E [ E ( X )2 } ] E ( X 2 ) 2 E ( X ) E ( X ) [ E ( X )2] E (X 2)[E (X )2] E (X2)E 2(X).
§4.1 数学期望
❖ 例2：某车站每天8:00—9:00,9:00—10:00都恰有一 辆客车到站，但到站的时刻是随机的，且两者到站的时间 相互独立。其规律为
8:10 8:30 8:50
到站时刻
9:10 9:30 9:50

《数学数学期望》课件

《数学数学期望》课件
《数学数学期望》ppt课 件
CATALOGUE
目 录
• 数学期望的基本概念 • 数学期望的性质与定理 • 数学期望的应用 • 特殊随机变量的数学期望 • 数学期望的扩展与展望
01
CATALOGUE
数学期望的基本概念
定义与性质
定义
数学期望是随机试验在大量重复 下出现的频率的稳定值。
性质
数学期望具有可加性、可数性、 线性性质等。
分位数与分位数函数
分位数
分位数是概率论中的一个概念，用于描述数据分布的位置特征。常见的分位数包括中位 数、四分位数等。分位数的计算和应用对于统计分析、数据挖掘等领域具有重要意义。
分位数函数
分位数函数是描述分位数与概率之间关系的函数。通过分位数函数，可以更方便地理解 和应用分位数的概念，从而更好地分析数据的分布特征。
通过计算投资组合的数学期望， 投资者可以了解投资组合的预期
收益，并据此做出投资决策。
数学期望在金融学中还用于资产 定价、风险管理、资本预算和股
票期权定价等领域。
在决策理论中的应用
在决策理论中，数学期望被用来评估 不同决策方案的预期结果。
数学期望在决策理论中还用于风险决 策、不确定性决策和多目标决策等领 域，以帮助我们做出更加科学和合理 的决策。
大数定律与中心极限定理
大数定律
当试验次数趋于无穷时，随机事件的频率趋于该事件 发生的概率。即 limn→∞P(|En−E)/n→0P(|En−E)/n→0limn→∞P(|En −E)/n→0=1。
中心极限定理
无论随机变量X1,X2,…,XnnX_1, X_2, ldots, X_{nn}Xi1,Xi2,…,Xinn的分布如何，当它们的数量趋于 无穷时，它们的平均值的分布趋于正态分布。即 limn→∞P(|En−μ)/σ≤z)=1−12z2lim_{n to infty} P(|En−μ)/σ≤z|)=1−12z2limn→∞P(|En−μ)/σ≤z|)=1 −12z2，其中En=1n∑i=1nXiEn = frac{1}{n} sum_{i=1}^{n} X_iEn=n1∑i=1nXi，μ是随机变量的均 值，σ是标准差，z是正态分布的分位数。

4 第 一节 数学期望精品PPT课件

4 第 一节 数学期望精品PPT课件

它的数学期望不存在
例3
按规定,某车站每天8 : 00 ~ 9 : 00 , 9 : 00 ~
10 : 00都恰有一辆客车到站 , 但到站的时刻是随机
的, 且两者到站的时间相互 独立 ,其规律为
8 : 10
到站时刻 9 : 10
8 : 30 9 : 30
8 : 50 9 : 50
概率 1
3
2
6
6
6
(1) 一旅客8：00到车站,求他候车时间的数学期 望
在这些数字特征中，最常用的是 期望、方差和协方差
第四章 随机变量的数字特征
数学期望 方差 协方差与相关系数
数学期望的引例
例如：某7人的高数成绩为90，85，85，80，80，
75，60，则他们的平均成绩为
90 85 2 80 2 75 60
7
90 1 85 2 80 2 75 1 60 1
例5 已知 X 服从0,2 上的均匀分布，求
Y sin X 的数学期望。
解
EY
E sin
X
sin
x
f
x
dx
因为
f
x
1
2
,
0 x 2；
0,
其它。
所以 E sin X 2 1 sin xdx 0
0 2
例6 设相互独立的随机变量X，Y的密度函数分别为
2x, (0 x 1) f1(x) 0, 其它
如何计算随机变量函数的数学期望? 一种方法是，因为g(X)也是随机变量，
故应有概率分布，它的分布可以由已知的X 的分布求出来. 一旦我们知道了g(X)的分布， 就可以按照期望的定义把E[g(X)]计算出来.
使用这种方法必须先求出随机变量函数 g(X)的分布，一般是比较复杂的 .
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1
1
84
1
.
13
例4.5 Xe(), 求EX?
f
(
x)
1
x
e
,
0,
x0 x0
E X x f(x )d x 1 x e xd x0x d (e x)
0
xex0 0exdx 0exd(x)ex0
(10)
提示: limxex x
lim x
x
x
0
e
.
14
三、随机变量函数的数学期望
0 x ,y 1 ,E (X Y )?
e lse
11
E ( X Y ) g ( x ,y ) f( x ,y ) d x d xx y ( x y ) d y
- -
设X表示掷一次骰子的得分, 则X的分布律为
X
x1
x2
x3
pk
1/6
3/6
2/6
求掷了N次的平均得分?
.
3
平 均 分 总 总 次 分 数 x 1 n 1 x 2 N n 2 x 3 n 3 x 1n N 1 x 2n N 2 x 3n N 3
nN1 f1当 N p116
平 均 分 x 1p 1 x 2p 2 x 3p 3
由此得出离散型随机变量的数学期望的定义
.
4
定义4.1 设离散型随机变量X, 它的分布律为
X x1 x2 … xn …
pk p1 p2 … pn …
若级数 xkpk绝对收敛, k1
则称其为X的数学期望(期望、均值),记为E(X),EX. 即
EXE(X) xkpk k1
.
5
注:
①EX是X在各次试验中的观察值的算数平均值的近似值
.
9
二、连续型随机变量的数学期望
连续型的是用”离散化”的方法, 由离散型的期望引入的.
设 连 续 型 r .v .X f(x ) .在 x 轴 取 密 集 分 点 x 1 x 2 x 3 , 则 X 落 在 小 区 间 [ x i,x i 1 ) 的 概 率 为
P { x i X x i 1 } x x ii 1f( x ) d x f( x i) x i P { X x i}
0
1
6
4 2 x 2(1 x )600(1 x )6d (x 2 ) 4 2 2 11x (1 x )6d x
6 16 1
60
0 (1x)7 (1x)70 0(1x)7
14xd[ ]14x
dx
1
7
7
1
1
7
20(1 x )7d x 20(1 x )7d (1 x ) 2(1 x )801
揭示随机变量取值规律的某些数字----数字特征
.
1
4.1 数学期望
一、离散型随机变量的数学期望 二、连续性型随机变量的数学期望 三、随机变量函数的数学期望 四、数学期望的性质 五、本节总结
.
2
一、离散型随机变量的数学期望
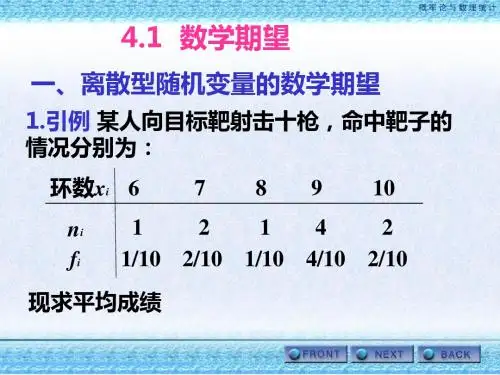
引例 掷一枚骰子
点数 1
2,3,4 5,6
得分 x1 x2 x3
次数 N n1 n2 n3
.
10
X
…
x1
x2
…
xn
…
pk
… f(x1)x1 f(x2)x2 … f(xn)xn …
E X x ip ix if(x i) x i x f(x )d x
i
i
定 义 4 . 2 设 连 续 型 r . v . X f ( x ) .若 积 分 x f ( x ) d x 绝 对 收 敛 , 则 EXE(X) xf(x)dx
.
11
例 XU(a, b), 求EX?
f
(x)
b
1
a
,
a x b
0,
else
1b
1 x2b
E X xf(x)dx xdx
baa ba2
a
1 b2a2 ab ba 2 2
.
12
例4.4
42x(1x)5, 0x1 f(x)
0,
else
E X x f( x ) d x 1 4 2 x 2 ( 1 x ) 5 d x 4 2 0 x 2 d [( 1 x ) 6 ]
.
6
例 XB(1,p), 求EX?
解 X的分布律为
X
0
1
pk
1p
p
E X 0 (1 -p ) 1 p p
.
7
例4.2 2个白球, 3个黑球, 任取3个. 记X为取到白球的个数, 求EX.
解 X的分布律为
X
0
1
2
pk
1/10 6/10 3/10
EX011623=6 10 10 10 5
.
8
称EX为 均值
EX反映了X取值的”平均状态”
②计算方法----上下相乘, 左右相加
③当X的取值为可数无穷多个时
为 保 证 级 数 x kp k 的 和 不 因 相 加 次 序 的 改 变 而 改 变 , k 1
则要求 xkpk绝对收敛. k1
④ 若 x kp k 不 收 敛 ,则 称 X 的 数 学 期 望 不 存 在 . k 1
第四章 随机变量的数字特征
随机变量X 用什么来研究X的”统计规律性”? 用什么来计算X取值的概率? ----分布函数F(X)
但是有些时候, F(X)不易求得或不必求得, 只要知道与X有关 的某些数值, 即可解决问题. 如, 比较3个班的数学成绩, 只要比较3个班的平均成绩(期望) 即可; 若其中2个班的平均成绩一样, 还需毕竟每个同学与该平均 值的差距(方差), 差距越小成绩越好.
例4.3 XP(), 求EX?
X的分布律为
P {Xk}ek
k!
k0,1,2,
E Xk P { X k }k e k e kk
k 0
k 0
k!
k 0 k!
提 示 :ex 1 xx2 xk xk
2 !
k!
k 0k!
E X e k e k 1 e e k 1(k 1 )! k 1(k 1 )!
.
15
例4.6
X
f(x) x3 2x2,
0x1 ; W55X.
0,
else
E W g (x )f(x )d x1 (5 5 x )(x 3 x 2 )d x
-
0
2
015x52x2125x3dx
x2
5x3
15x4
1
35
5 2 2
3
2
4
0
24
.
16
例
(X ,Y )
f(x ,y ) x 0 ,y ,
Th4.1 一元函数 Y=g(X)
g(xY)E[g(X)] i1
- g(x)f(x)dx, X为 连 续 型
Th4.2 二元函数 Z=g(X,Y)
EZE[g(X,Y)]
g(xi,yj)pij,
i1j1
(X,Y)为 离 散 型
- - g(x,y)f(x,y)dx, (X,Y)为 连 续 型