1-3傍轴条件下的单球面折射成像解析
- 格式:ppt
- 大小:784.50 KB
- 文档页数:21

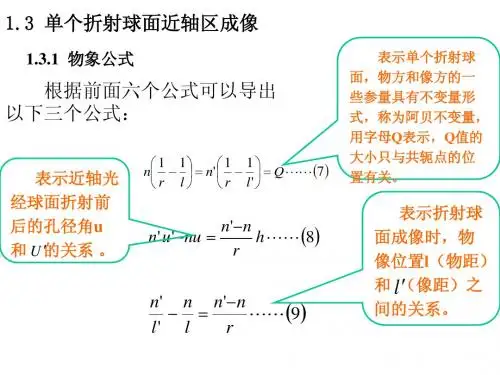
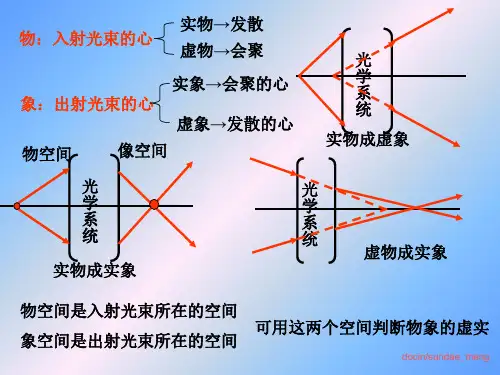

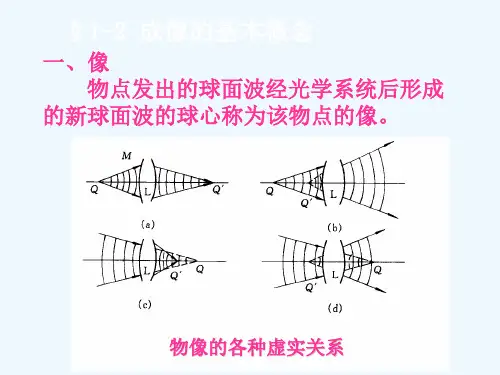
引言(绪论)光学中以光线概念为基础研究光的传播和成像规律的一个重要分支是几何光学.在几何光学中,折射定律的发现标志着光线传播定律的最终确立,费马原理即是解释、证明和概括光线传播实验定律的途径之一. 本文依据费马原理,推导出了近轴光线条件下的单球面物像折射公式.应用近轴光线条件下的单球面物像折射公式,可以推导出多种情况下的成像公式,为研究复杂的光学系统成像提供了基础性的理论依据,以说明单球面物像折射公式在几何光学中的基础重要性.1 符号法则为了研究光线经由球面反射和折射后的光路,必须先说明一些概念以及规定适当的符号法则,以便使所得的结果能普遍适用,方便读者阅读.图1 主平面内的球面反射图1中的AOB表示球面的一部分.这部分球面的中心点O称为顶点,球面的球心C 称为曲率中心,球面的半径称为曲率半径,连接顶点和曲率中心的直线CO称为主轴,通过主轴的平面称为主平面.主轴对于所有的主平面具有对称性.因此只需讨论一个主平面内光线的反射情况.图1表示球面的一个主平面.在计算任一条光线的线段长度和角度时,对符号作如下规定:(1)线段长度都从顶点算起,凡光线和主轴的交点在顶点右方的,线段长度的数值为正;凡光线和主轴的交点在顶点左方的,线段长度的数值负.物点或像点至主轴的距离,在主轴上方的为正,下方的为负.(2)光线方向的倾斜角度都从主轴(或球面法线)转向有关光线时,若沿顺时针方向移动,则该角度为正;若沿逆时针方向转动,则该角度为负(再考虑角度的符号时,不必考虑组成该角的线段的符号).(3)在图中出现的长度和角度(几何量)只用正值.例如s表示的某线来表示该线段的几何长度.下讨论都假定光线自左向右传段的值是负的,则应用s播.(4)特俗情况下的,文中均在相应位置另有特殊解释说明.2 单球面物象折射公式的推导2.1 球面折射的一般分析设有两种透明均匀的各向同性的介质,界面∑为球面的一部分,两侧介质折射率分别为n 和'n 且n<'n ,如图2所示,折射球面∑的曲率中心C 与顶点O 的连线为主光轴,简称主轴(∑面关于主轴的旋转对称面).图2 光在单球面上的折射设主光轴上面顶点O 的左方有一真实发光点P ,他发出的同心光束的任意一条光线自左向右入射到∑面上的M 点,相应的折射与主轴交与'P 点.以球面顶点O 为计量原点,记球面曲率半径,'',,OC s OP s OP r ===,l PM =''l MP =ϕ=∠MOC . 则PMP’的光程为∆'PMP =''l n nl +在PMC ∆和'MCP ∆中应用余弦定理,并注意()ϕπϕ--=c o s c o s()r s PC +-= r s CP -=''可得 ()()ϕcos 222s r r r s r l --+-=()()ϕcos '2''22r s r r r s l -++-=因此,光线PMP 的光程可写成∆'P M P =ϕϕcos )'(2)'('cos )(2)(2222r s r r s r n s r r s r r n -+-++---+ 式(2-1)根据费马原理,光程变化率应为0,即0d d =ϕl 式(2-2) 代入∆'PMP 的表达式进行求导,有ϕϕϕϕcos )'(2)'(sin )'(2'cos )(2)(sin )(22222r s r r s r r s r n s r r s r r s r r n -+-+--=---+-经计算整理后可得到⎥⎦⎤⎢⎣⎡-+---=---)'('1)(1)cos 1(2)'('')(22222222r s n s r n r r s n s s r n s ϕ 式(2-3) 给定s 和ϕ可由式(2-3)定出.一般来说,'s 与ϕ有关,这意味着由同一P 点发出的同心光束中的各条光线,经∑面折射后,不再汇交与一点,即球面折射破坏了光束的同心性,使轴上发光点不能成像.有两种特殊情况值得注意.其一,令式(2-3)两端同时等于零,即222222)'('')(s r s n s s r n ---=0 式(2-4))'('1)(122r s n s r n -+-=0 式(2-5)求解这组联立方程的解,从而把s 和s’同时确定下来,它们均与ϕ无关,此时的P 和'P 是一对特殊的共轭点,称为球面折射的齐明点或不晕点.对一对齐明点,宽光束经球面折射后仍能成像.其二是把光束限制在近轴区域内,即1cos ≈ϕ,此种的讨论,详见下文.2.2 近轴光线的单球面折射2.2.1 物象距公式在近轴光线的条件下,ϕ值很小,在一级近似下,1cos ≈ϕ,因此式(2-3)中的0)cos 1(≈-ϕ,'s 与ϕ近似无关,则有 222222)'('')(r s n s r s n s -=- 式(2-6)将上面等式两端同时开放,经数学处理后,可得如下简单关系式: rn n s n s n -=-''' 式(2-7) 上式表明,在n 、'n 和r 给定的条件下,在近轴区,轴上物点P 经球面∑折射后可在轴上得一相应的像点'P .从球面顶点O 到像点'P 的距离's 称为像距;从球面顶点O 到P 的距离s 称为物距;'n 和n 分别称为像方折射率和物方折射率,式(2-7)称为球面折射近轴成像的物象距公式.此式对凹球面同样成立.2.2.2 焦距公式如果位于主轴上的物点位置改变,则与之共轭的像点在主轴上的位置必有相应改变.轴上无限远处物点的共轭像点称为折射面的像方焦点,记作'F ;面顶点O 到像方焦点'F 的距离称为像方焦距,记作'f ,轴上无限远处像点的共轭物点称为折射球面的物方焦点,记作F ;球面顶点O 到物方焦点F 的距离称为物方焦距,记作f .由前文关于物距、像距的的符号规则可知:当'F 在O 点右方时'f >0,在O 点左方时'f <0;当F 在O 点左方时f>0,在O 点右方时f<0.根据式(2-7)及上述焦点的定义,可知:当 -∞=s 时nn r n s f -=='''' 式(2-8) 当 ∞='s 时 n n nr s f --==' 式(2-9) 可见,折射球面的两个焦距与它的几何形状(r )及其两侧介质折射率(n ,'n )有关,由式(2-8)和式(2-9)可得两个焦距之比为 nn f f ''-= 式(2-10) 上式表明,折射球面的两个焦距数值一般不等,但符号相反,因此,相应的两个焦点必定分居球面顶点两侧不等距离处.2.2.3 球面折射近轴物点近轴成像如图2所示,主轴上的P 、'P 是一对共轭点.设想将主轴绕折射球面曲率中心C 并在图面内沿顺时针方向旋转一小角度θ,主轴变成副轴,P 、'P 点分别转到Q 、'Q 点.由于球对称性,Q 、'Q 必然也是一对共轭点,这就证明了近轴物点可以成像.由于θ角很小(在近轴区),可以认为弧PQ ≈PQ ,弧''Q P ≈''Q P ,且''P Q QP 和近似地垂直于主轴,P 、'P 点分别是Q 、'Q 点在主轴上的的垂足,所以s 和's 分别为近轴物点Q 的物距和像点'Q 的像距,它们满足式(2-7).近轴物点及其共轭像点到主轴的距离分别为物高和像高,用y 和'y 表示.引入横向放大率β,其定义为像高和物高之比,即 yy '≡β 式(2-11)在近轴区的条件下,i i =sin ,又由折射定律,可得''i n ni = 式(2-12)图3 单球面折射近轴物点成像即有 ⎪⎭⎫ ⎝⎛-=⎪⎭⎫⎝⎛-'''s y n s y n 式(2-13) 由式(2-11),可以得到横向放大率公式 sn ns ''=β 式(2-14) 3.单球面物像折射公式的应用3.1 高斯公式的推导把式(2-8)和式(2-9)代入式(2-7)可得,''''f n f n s n s n =-=- 或 1''=+sf s f 式(3-1) 此式便是普遍的物像公式,称为高斯物像公式.3.2 牛顿公式的推导如图4,在确定物点P 和像点'P 的位置后,我们把物距和像距分别从物方焦距和像方焦距算起.物点在F 之左的,物距FP 用x -表示;像点在'F 之右的,像距P F '用'x +表示.反之亦然.这样就有()()f x s -+-=- ()()'''x f s +++=图4 顶点为物方和像方焦点时的物距和像距示意图代入式(3-1)可得1'''=+++fx f f x f 即有''ff xx = 式(3-2) 此式便是牛顿公式.3.3 近轴光线单球面反射公式的推导对于反射情况,这里利用焦距和折射率的关系,从两方面入手进行讨论与推导.下面先就焦距与折射率的关系开始进行讨论.关于焦距和折射率的关系,已在上文中给出了具体的关系式,即式(2-10). 在球面反射的情况中,物空间与像空间重合,且反射光线与入射光线的传播方向恰恰相反.这一情况,在数学处理上可以认为像方介质的折射率'n 等于物方介质折射率n 的负值,即nn -='(这仅在数学上有意义)。