当前位置：文档之家 › 1-3傍轴条件下的单球面折射成像资料

1-3傍轴条件下的单球面折射成像资料

  • 格式：ppt
  • 大小：563.50 KB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

物象关系式2

物象关系式2
点到光轴的距离远小于球面曲率半径傍轴小物以傍轴光线成像三傍轴球面折射的物象关系式物像关系式p定义光焦度单位m1表征处于确定介质中的球面的光学特性
光程定义:光波在介质中所经历的几何路程 l与介
质折射率n之积 nl 。
[L] nl
[l] l cv
n1 n2 …… nm
……
l1 l2
lm
物理意义为：光程表示光在通过介质中真实路程 l 所需的的
时间内，在真空中所能传播的路程 。
光程有可加性 [L] = ( ni li )
费马原理—— 光沿光程取极值的路径传播。
[l]
B A
nds
0
§3 单球面反射和折射
一.符号法则：
1.长度量:由指定的原点量起,方向与光的传播方向一致为正,反之为负. 规定光线自左向右传播. 原点(参考点)左边为负右边为正；
n' p
p'
p
平面折射
n n p' p 0
p' n' p n
Φ0
np'
n' p
高斯公式 f ' f 1 p' p
f ' n' fn
y' f x'
y
x
f'
牛顿公式 x x' f f '
像倒立
像正立
像缩小； ，像放大。
以傍轴光线成像 P2
y
像空间
P` u
空气介 质n2
x
n1
P物点
水介质
物空间
傍轴光线：与光轴成微小角度 sin u tnau u
傍轴小物：点到光轴的距离远小于球面曲率半径
三、傍轴球面折射的物象关系式

光在单球面上的折射和反射-四川大学

光在单球面上的折射和反射-四川大学
β =−
x′ f′
y′ f =− y x
从 Q 作 O 点的入射线 QO ，其折射线是 OQ′ 。由图可知，得
ny n′y′ =− −s s′
或 讨论：
β=
y′ ns′ = y n′s
(1) β > 0 时， y′ 与 y 同号。物正立时像也是正立的。即物是实物时，像必定是虚像，反之， 当物是虚物时，像必定是实像。 (2) 当 β < 0 时，物和像在主光轴的异侧，而且当物是实物时，生成的像也是实像，当物是虚 物时，生成的像也是虚像。 总之，当 β > 0 时，物和像一定是一实一虚； 当 β < 0 时，物和像的虚实相同。
n n’ P n n’
P’
P’ P
虚物成实像
虚物成虚像
n′ n n′ − n − = s′ s r f′ f + =1 s′ s xx′ = ff ′
1 1 2 + = s′ s r 1 1 1 + = s′ s f xx′ = f 2
φ=
f′=
n′ r n′ − n n f =− r n′ − n
n′ − n r
φ=
f′ n′ =− f n
β=
ns′ n′s
N
P
F
(e) 轴上物点成像作图法
图 作图法的几个例子
四川大学精品课程《光学》
六．球面反射镜 1．方法：将反射看作是折射的特殊情况 2．球面反射的物像距公式：
1 1 2 + = s′ s r
i = −i′ ； n′ = −n
3． 单球面折射饿球面反射镜公式对比
球面折射和球面反射公式对照表 球面折射成像 球面反射成像 公式 公式 物 像 距 焦距和光焦度 横向放 大率

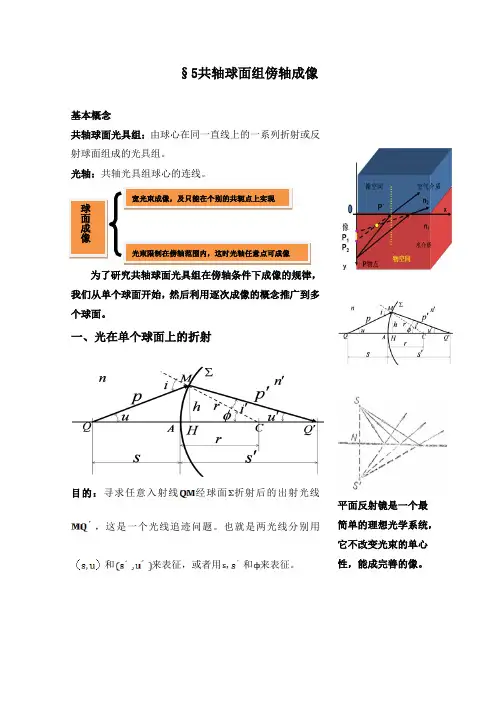
1.5共轴球面组傍轴成像

1.5共轴球面组傍轴成像

思考：何时具有同心性呢？何时接近具有同 心性呢？
OPTICS
同心性问题
s2 s2 2 2 2 n (s r ) n (s r )2 1 1 2 4r sin ( / 2) 2 2 n (s r ) n (s r )
给定s，只有满足下式， s’不随 变化。
y 0 或 y' 0
'2 2 '2 2
轴外共轭点的旁轴条件：
y , y s , s , r
2
b、横向放大率公式 y' 定义： V y
折射球面的横向放大率公式：
y i s
，
y' i' ， s'
ni n' i'
y' ns' V y n' s
反射球面的横向放大率公式：
d O
s'
2）其余规定与单球折射面成像的符号法则相同
1 1 2 s' s r
n
P
l l
C
P
h h
r f f ' 2
r
S
S
r
小提示：同样是实像时为正，虚像时为负。
推论： 光在单个平面上的折射、反射成像
r→∞时，球面→平面，球面折射和反射成像→平面 折射和反射成像，且有 傍轴光线在平面上的折射成像公式：
O1
-y ' P'
s1
s1'
d12
s2
s2'
s 3'
共轴球面组的逐次成像
单个球面光具组的逐次成像：前一个球面光具组的出射光束（像）—— 后一个球面光具组的入射光束（物）

5共轴球面组傍轴成像

5共轴球面组傍轴成像

§5共轴球面组傍轴成像基本概念共轴球面光具组：由球心在同一直线上的一系列折射或反射球面组成的光具组。

光轴：共轴光具组球心的连线。

为了研究共轴球面光具组在傍轴条件下成像的规律，我们从单个球面开始，然后利用逐次成像的概念推广到多个球面。

一、光在单个球面上的折射目的：寻求任意入射线经球面折射后的出射光线，这是一个光线追迹问题。

也就是两光线分别用和来表征，或者用,和来表征。

平面反射镜是一个最简单的理想光学系统，它不改变光束的单心性，能成完善的像。

在和中，有折射定律和以下几何关系(1)正弦定理余弦定理由上（1）（2）（3）可得由（4）（5）得取（6）平方，把（7）（8）带入得化解得由上式可见给定和，便可定出，一般来说与有关，这就是说同一物点，光线方向不同时，即不同时，折射后的光线与主光轴的交点是不同的。

即同心光束经球面折射后，失去同心性。

从成像的角度来讨论问题，我们关心的是在什么条件下与无关，从而成像于。

1、非傍轴成像与无关，从而成像于，如果我们把方程两边都等于，且去掉项。

有由上方程组可把同时确定下来。

只能在个别的共轭点上实现二、轴上物点成像焦距、物像距公式1、单球面折射成像欲使折射光线保持同心性，必须满足近轴（傍轴）条件，对于轴上物点来说，近轴（傍轴）条件应为用角度来表示则有由于很小，，。

（10）式右端为0，有化为上式表明，对于任一个，有一个，它与角无关，这就是说在傍轴条件下轴上任意物点Q 都可成像于某个点，故上式中的、，分别称为物距和像距，上式便是单个折射球面的物像距公式。

物方焦点（第一焦点、前焦点）：轴上无穷远像点的共轭物点。

像方焦点（第二焦点、后焦点）：轴上无穷远物点的共轭像点。

物方焦距（第一焦距、前焦距）：像方焦距（第二焦距、后焦距）：当得物像方焦距公式：两者之比为则物像距公式（12）可用焦距表示为二、符号法则假设光线自左向右入射，物点在球面顶点左侧，像点在球面顶点右侧。

线段和角度的符号规定如下:（1）物点在顶点左侧(实物)，物距s>0；物点在球面右侧(虚物)，物距s<0。

《光学教程》第五版 姚启钧 第一章 几何光学

《光学教程》第五版 姚启钧 第一章 几何光学
B'
B'
利用 物方焦平面 作图 光心
利用 物方焦点 作图 象方焦平面
利用 象方焦平面 作图 光心
四、 物像之间的等光程性
物点和像点之间各光线的光程相等。
F
F'
例1-3. p36 已知薄透镜 f ' 12cm, 问：
（1） 球面完全对称，折射率n=1.5，求曲率半径R；
（2） n1=4/3, n2=1 r2=R， f ' 12cm求, 曲率半径r1。
A ╭r φ-li''u'╭ n' P′
P -p
O
-y'
p'
笛 卡 儿 符 号 法
则
(3) 角度（以锐角量度）
｛ 以主轴转向考虑的光线 顺时针为正 逆时针为负
(4) 全正图形 图中标记的是线段或角度的绝对值（如上)
二、傍轴条件下单球面折射的物象公式
在下图中，当u,u’ 很小时， 称为傍轴条件
n -i
n
P
F’
P’
x'
-p’
-f ’ -p
-x
n′
F
f
六、 傍轴物点成像的放大率 亥姆霍兹-拉格朗日定理
1. 横向放大率
y pi y' p'i'
ni n'i'
n
y -x • P F•
-f i
-p
y' y
n p' n' p
利用-p=-(f+x),p'=(f '+x')
及牛顿公式，得
f x'
第一章几何光学基础11几何光学基本规律12光程费马原理13棱镜和最小偏向角全内反射和光学纤维14同心光束和象散光束物和象15单球面上的傍轴成象内容16薄透镜的成象规律17理想光学系统的基点和基面18共轴球面系统组合的理论19空气中的厚透镜薄透镜组110一般理想光具组的作图求像法和物像公式11几何光学的基本原理11光源

基础光学

基础光学

第一章 几何光学
§1.1几何光学的基本定律和费马原理 1.1 基本定律 光源、 点光源、 光线、 光束 1 .光的直线传播定律 2 .光的独立传播定律 3 .光的反射定律 4 .光的折射定律 由上述定律可得出光路可逆性原理。
* 几何光学实验定律成立的条件
1.
被研究对象的几何尺寸D远大于入射光波 波长 D/ >>1 衍射现象不明显，定律适用。 D/ ~ 1 衍射现象明显，定律不适用。
( n1 l1 n2 l 2 ) 0 x ( n1 l1 n2 l 2 ) 0 的路径。 z
将l1、l2的表达式代入上式有
l ACB n1l1 n2 l 2
其中： l1 y ( x x1 ) z
2 1 2
l2
y
2 2
2 2
物和像
物点和像点：实物、虚物 、实象、虚象
物面和像面：物点、像点的集合
光学系统: 单个或多个光学元件组成的系统 物方空间：实际的入射光线所在的空间 像方空间：实际的出射光线所在的空间 对应的有物方折射率和像方折射率
Ⅰ
Ⅱ
S2 S1’
S2’ S3 S3’
Ⅲ
n1
n2
n3
n4
2. 2 理想光学系统 同心光束通过系统后仍能保持为同心光束 理想光学系统成像的性质： 1 . 物象之间的共轭性；
前 言
一、光学的研究对象及学习光学的意义 1. 光学的研究对象 光学是研究光的本性、光的产生与控 制、光的传输与检测、光与物质的相互作 用，以及它的各种应用的学科。 2. 学习光学的意义 光学是物理学中一门重要的基础学科， 也是一门应用性很强的学科。
二、 光学发展简史 光是什么？

第二章几何光学成像

第二章几何光学成像
光轴－－各折反射球面的球心所在的一条直线上
光线与光轴的夹角小于 5 0 时，有sin ≈tan ≈ ，
光学系统满足这样条件的区域，轴上发出的同心光束， 经系统变换后，仍为同心光束，近轴条件限制了光线与光轴 的夹角。
在近轴条件下，单球面折射系统可视为理想光学系统， 同心光束经其变换后，可认为仍具有单心性。
像空间--- 经光学系统变换后的光束所在的几何空间。 它包括所有的实像点．虚像点所在的几何空间。
说明：
① 对于给定的光学系统，无论物与像是实是虚，均具有共轭特点， 这是光路可逆性原理的必然结果。
② 实物、实像的意义在于有光线实际发自或通过该点，而虚物、 虚像仅仅是由光的直线传播性质给人眼造成的一种错觉，实际上 并没有光线经过该点。
上页 下页
2.光在单个球面上的折射 －－光在两介质分界面发生折射，界面是球面的一部分。
y
•
n p
u
i M i
h AH
n n
p’ C
u
Q'
y•
s
r
s
Q
n：物方介质的折射率
Q：物点
n'：物方介质的折射率
Q'：像点
C：球心
顶点：球面在光具组中的对称点A
光轴：使光线不发生偏折的方向，如过球心并垂直于球面的方向
s
s
在上图折射系统中, A和A是一对共轭物像点, u
和 u 是一对共轭角. 我们定义角放大率为
u,
u
(1-4-9)
上页 下页
由上图可得
u s ,
u
s
因为 y ns , y n s
因此有
所以 s ny . s n y
nu ynuy.

第2篇单球面成像

第2篇单球面成像

单球面折射时近轴与远轴像点位置：
1、近轴光路计算公式
l- r
i=
u
r
(3－5)
i ′ = i n / n′
(3－6)
u′= u + i - i′
(3－7)
i′ l′= r + r
u′
(3－8)
将（3-5）~（3-8）式经过整理，得到
n’ l r l ’=
n’ l －n l + n r
(3－9)
上式表明，对一定的折射球面，近轴光线的像点位置l ’ 只是物点位置l 的函数，而与孔径角u 无关。这表明近
轴光线所成的像是完善的。通常把近轴光线所成的像点 称为“高斯像点”。通过高斯像点而垂直于光轴的像面 称为“高斯像面”。 近轴区的成像关系称为近轴光学 （也称为Gaussian Optics)。
2、三个常用的物像共轭位置关系式：
符号规则的应用意义：
20º
20º
20º
20º
100
100
符号规则的应用：
符号规则的应用意义及注意点：
• 光路图中所有几何量一律以绝对值标注，负号则 表示该几何量的方位。
• 应用一定形式的公式可进行各种光路的正确计算。 • 推导公式时，也要使用符号规则，以便使导出的
公式具有普遍性。
单球面成像：
一、符号规则（2）
• 角度： 一律以锐角来度量，规定顺时针为正，
反之为负。 1. 起始轴和转动方向：
U、U ’ —— 由光轴起转到光线； I、I ’ —— 由光线起转到法线；
φ —— 由光轴起转到法线。
符号规则的意义：
• 可使某种情况下推出的公式普遍使用于各种情况。
符号规则会直接影响公式的形式，而应用一定 形式的公式时就必须遵守一定的符号规则。否则， 由于符号弄错了，即使公式和运算都正确，而其 所得的结果仍然是错误的。

第二章-球面和球面成像系统

第二章-球面和球面成像系统
不同 U 的光线经折射后不能相交于一点
n
E
n’
A
C
O -240mm
同一物点发出的物方倾斜角不同的光线过光组后并不能交于一点！
点－》斑 ——不完善成像！ ——球差（像差）
。在光学上称其为弥散斑
一个物体是由无数发光点组成的，如果每个点的像都是弥 散斑，那么物体的像就是模糊的。
将物方倾斜角U 限制在一个很小的范围内，人为选择靠近光轴 的光线，只考虑近轴光成像，这时可以认为可以成完善像
的截距 L=-240mm，由它发出一同心光束，今取U为-1°、-2 °、
-3 °的三条光线，分别求它们经折射球面后的光路。（即求像
方截距L’ 和像方倾斜角U’ ）
n
E
n’
A
C
O -240mm
• U= -1°: U’= 1.596415° L’=150.7065mm • U= -2 °: U’= 3.291334° L’=147.3711mm • U= -3 °: U’= 5.204484° L’=141.6813mm 由 以上几个公式可得出L一定, L' 是U的函数
sin I ' n sin I
（2－1） （2－2）
近 轴 光 线
i lru r
i' n i n'
n'
成
像
ቤተ መጻሕፍቲ ባይዱ
U' U I I'
公
像 u' u i i'
公
式 L' r(1 sin I ' ) （2－4） 式 l' r(1 i' )
sinU '
u'
大L公式

单球面折射、共轴球面系统

单球面折射、共轴球面系统
n2 n1
3）、第二焦点(the second focal distance)
第二焦点：与无穷远处物体所对应的像点，用F2表示。 第二焦距：F2到折射面顶点的距离，用f2表示。
将u =∞代入单球面折射
公式得： F2
f2
n
4）、焦度与焦距的关系
n2 n1 r
f1
n1r n2 n1
Φ
n1 f1
n2 f2
若 n=1, 则：Φ=1/f
n1 u
n2 v
n2
r
n1
f1 u
f2 v
1
单球面折射成像公式
例题
圆柱形玻璃棒（n=1.5）的一端是半径为2cm的凸球面。 求:（1）当棒置于空气中时，在棒的轴线上距离棒端 外8cm处的物点所成像的位置。 （2）若将此棒放入水（n=1.33）中时，物距不变，像 距应是多少(设棒足够长)？
例题
有一玻璃球（n=1.5)的半径为10cm，一点光源放在 球前40cm处，求近轴光线通过玻璃后所成的像。
解：对第一折射面而言，
u1=40cm ，r=10cm,
n1=1
n1=1，n2=1.5，求v1
O P1
1 40
1.5 v1
1.5 1.0 10
P2 I I1 n2
得：v1=60cm
I1距P1为 60cm，为第二球面的虚物，故： u2=d-v1=20-60=-40cm，r=-10cm， n1=1.5 ，n2=1 , 求v2，
1.5 40
1 v2
1.0 1.5 10
得：v2=11.4cm，为实像。
nh 1 u
nh 2 v
(n 2
n1
)h r
小结：
n1 u
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y ' ns ' #
y n's
f ' n' ，代入 #式，得 fn
f x'
x f'
2)
tan(u) h u Q
s
y
n
l -u
tan(u) h u s
P -s
代入#式，得：
y y
nu n u
-i A n’
h -i’ l’
d
u’
O rC
P’ -y’
s’
Q’
拉格朗日—亥姆霍兹不变式
y' y
P Q C ∽ P Q C , yP C s r
y P Cr s
由 物 像 公 式 n ' n n ' n ， 变 形 得 ： s r n s
s ' s r
s r n s
y' ns' #
y n's
12
1)利用s ( f x),s' ( f ' x'), 牛顿公式xx' ff ',
焦物距x：物方焦点到物点的距离
焦象距x'：象方焦点到象点的距离
n -x -f
•P F• -s
n'
f'
x' P’
F• ' •
s'
f f 1 s s
根据上面的定义, 有：s=x+f , s'=x'+f '
代入高斯公式，得
f ' f 1
f 'x' f x
整理得 xx'ff' ---牛顿公式(普适公式)
1-3傍轴条件下的单球面折 射成像
单独一个球面不仅是一个简单的光学系 统，而且光学仪器中透镜的表面都是球面的 ，因而球面是组成光学仪器的最基本单元。 研究光经球面折射（和反射）是研究一般光 学系统成像的基础。
2
三、近轴条件下的物像公式
nl''nl 1rnl''s'nl s
如果， l s,l' s', 即u,u’张开角度很小，
➢ 球面反射时： f ' r f
9
2
四、高斯公式、牛顿公式
1、高斯公式 由 n nnn 两边除以光焦度
s s r
n n r
f
n n'
n
r
f'
n' n' n
r
得
nr 1nr11 nns nns
将焦距公式代入
得
f f 1 s s
---高斯公式(普适公式)
对任何理想成像过程均适用
10
2. 牛顿公式
——近轴条件 成像公式近似为：
n' nn'n
P
n
-i1
l
-u
O
A -i2 l ' n’ u’ rC
P`
s' s r
-s
s’
——近轴条件下的物像公式
讨论：
① 当介质和球面一定时（n,n’,r 一定），s‘与s一一对应，即： 在近轴光线条件下光束单心性得到保持。
② 物像共轭：P物P‘像；P‘物P像
③ 对凹球面折射同样适用
n
n′ P1′
O2
P2′
s1′
-s2
-s2′
由 折 射 成 像 公 式n' nn' n s1' s1 r1
得 :s1' n'n'r 1nsn1代 入 数 据16cm
s1′为正，所以中间像P1′与物分居球面两侧，即在顶点右侧，
是实像
16
例：一个折射率为1.6的玻璃哑铃，长20cm，两端的曲率半径
反射系统由 值辨别物像性质的原则与折射系统相同
15
例：一个折射率为1.6的玻璃哑铃，长20cm，两端的曲率半径
为2cm。若在离哑铃左端5cm处的轴上有一物点，试求像的位
置和性质。 n
[解]：两次折射成像问题。 P O1
1) P为物对凸球面O1折射成像P1′ -s1
已 知 :s 1 5 ,r 1 2 ,n 1 ,n ' 1 .6
当 s 时,由物像公式得 :
f
'
s'
n' n'
n
r
n'
像方焦距
B. 物方焦点F、物方焦距f
n
n` F`
-s
O s’
f`
当s' 时 ,由 物 像 公 式 得:
n F
n
n
f s r
n' n
物 方 焦 距 -s -f
f'
n'
C.
fn
➢ ∵ nn' f f'
n` O s’
➢ “-”号表示 f 与 f ’永远异号，物、像方焦点一定位于球面两侧
[注]在球面折射中,
n' s'
n s
n' n , r
f' s'
f s
1, xx'
ff
'三者等效11
五、垂轴小物成像和放大率
近轴条件： 垂轴小物、 近轴光线
像也垂轴， 物与像相似
n Q
y
l -u
P -s
-i A n’
h -i’ l’
d
u’
O rC
P’ -y’
s’
Q’
1、横向放大率：像与物的横向大小之比
即： nuynyu （傍轴条件下，物像空间各共
轭量的关系）
13
[注] 像的性质判断（也适用于球面反射）：
y' ns' nu
y n's nu
0 正 立 像（虚实相反）实物虚像或虚物实像
0 倒 立 像（虚实相同）实物实像或虚物虚像
1 放 大 像 1 缩 小 像
2、角放大率：一对共轭光线与光轴的夹角u'与u之比
[课下练习]也可用高斯公式、牛顿公式求解！
17
3)若P是一定高度的垂轴小物， n
④ 平面 r, 则 s ' n ' s
6
n
讨论：
n' nn'n
⑤ 在球面反射中，物像空间重合，且入射光 s' s r
线与反射光线行进方向相反，在数学处理 方法上，可假设n‘= -n (物理上无意义)则， P -s
s’ P’
物象公式为： 1 1 2 s' s r
⑥ 当介质和球面一定时（n,n’,r 一定），*式右端一个常量
u u
sn 1 s n
n Q
y
l -u
P -s
-i A n’
h -i’ l’
d
u’
O rC
P’ -y’
s’
Q’
[注] 角放大率和横向放大率的关系
n,
n
14
3、球面反射的放大率：
y'
y
s' s
uu
[注] 在笛卡儿坐标系下，反射系统的实象和虚象 对应的像距的正负与折射系统恰相反. 对于反射系统：s′<0为实象，s′>0 为虚像; 对于折射系统：s′<0为虚像，s′>0 为实像.
定义 n'n ——球面的光焦度 r
单位：m－1，称为屈光度，用D表示。1D＝100度
物理意义：表示光进入光学系统的折光程度——折光度
0 为会聚系统， 0 为发散系统， = 0 为无焦系7统.
n'n r
球面反射 2n r
8
⑦ 焦点、焦距 A. 像方焦点 F’、像方焦距f ’
n' nn'n s' s r
为2cm。若在离哑铃左端5cm处的轴上有一物点，试求像的位
置和性质。
2) P1′为物对凹球面O2折射成像
已知:s2 20164,
r22,n1.6,n' 1
n P
O1 -s1
n
n′ P1′
O2
P2′
s1′
-s2
-s2′
同 1有 :s2 ' n' n'r 2nsn 2 代 入 数 据 10cm
s2′为负，所以最后的像P2′与中间像P1′同侧，是一个虚像， 正好落在哑铃的中央