当前位置：文档之家 › 第三章几何光学球面反射折射物像公式

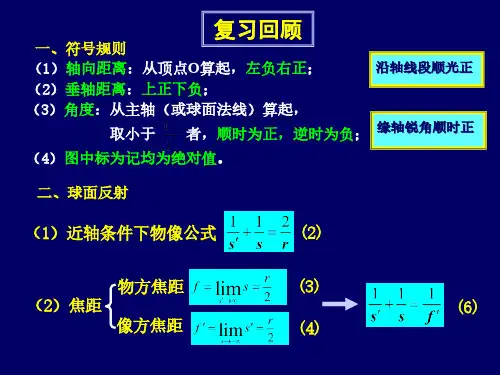
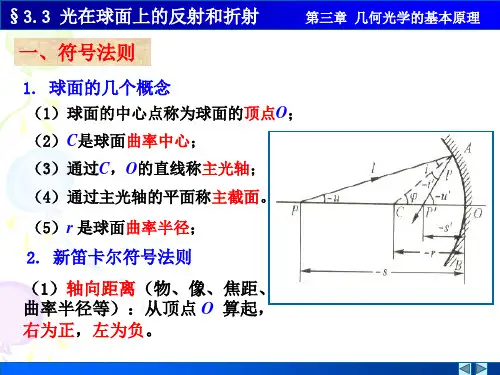
第三章几何光学球面反射折射物像公式

  • 格式：ppt
  • 大小：1.65 MB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

第三章几何光学的基本原理-卓士创($5-6)

第三章几何光学的基本原理-卓士创($5-6)

其中：
(17)——横向放大率
(18)——角度放大率
(16)
推广：对于共轴光具组,理想成像应满足亥——拉定理,即
(19)
小结
一、 近轴物近轴光线条件下的球面反射
(1) 物象公式
(11)
(2) 横向放大率
(12)
二、近轴物近轴光线条件下的球面折射
（1）物象公式
(13)
（2）横向放大率
(14)
倒立象 ;
（2）公式：
（8）
由图知：
所以有：
近轴光线、近轴物物件下！
（9） ——也适用于单个球面
将
、
代入上式有：
说明：
（1）
，表示放大；
，表示等大；
（2） 对实物而言： ，表示像相对物正立；
对虚物而言： ，表示像相对物倒立；
（10）
，表示缩小。 ，表示像倒立。 ，表示像正立。
参图
小结
一、近轴条件下的薄透镜成像公式
已知： f1’= -f1 =2cm， f2’=-f2=2cm ， -r =8cm。试求：(1) d12= 5cm， d23= 10cm，-s2 =1cm ，叉丝P经光学系统成像的位置: S1’ (经L1) 、 S2’ (经L2) 、 S3’ (经L3) 、 S4’ (回经L2) 、 S5’ (又经L1) =? (2)当d12= 5cm时，目镜L1能成1个清晰叉丝像， d23=?
令
球
令
——球面折射公式（2）
面
反
射
令焦距
公
式
⑸
——球面折射公式（3）——高斯公式
由
、
——球面折射公式（4）——牛顿公式
例题3.4 一个折射率为1.6的玻璃哑铃，长为20cm，两端的曲 率半径为2.0cm．若在离哑铃左端５.0cm处的轴上有一物点，试 求像的位置和性质。

光的折射与反射的计算公式

光的折射与反射的计算公式

光的折射与反射的计算公式在光学中，折射和反射是两种重要的现象。

当光线从一种介质传播到另一种介质时，会发生折射现象；而当光线遇到边界面时，会发生反射现象。

本文将介绍光的折射和反射的计算公式。

一、光的折射光的折射是指光线从一种介质传播到另一种介质时的偏转现象。

根据斯涅尔定律，光线在垂直于边界面的法线上的入射角和折射角之间的关系可以用下面的公式来表示：n1*sinθ1 = n2*sinθ2其中，n1和n2分别代表光线所处的两种介质的折射率，θ1为入射角，θ2为折射角。

二、光的反射光的反射是指光线遇到边界面后返回原来介质的现象。

根据反射定律，入射角和反射角之间的关系可以用下面的公式表示：θ1 = θ2其中，θ1为入射角，θ2为反射角。

三、计算案例现假设有一束光从空气（折射率为1.00）射入玻璃（折射率为1.50）中，入射角为30度。

我们可以利用光的折射公式来计算光线的折射角。

代入数据，可以得到：n1*sinθ1 = n2*sinθ21.00*sin30 = 1.50*sinθ20.50 = 1.50*sinθ2sinθ2 = 0.50 / 1.50sinθ2 ≈ 0.3333θ2 ≈ arcsin(0.3333)θ2 ≈ 19.47度因此，光线在射入玻璃中的折射角约为19.47度。

四、结论光的折射和反射是光学中的基本现象，通过计算公式可以准确地计算出光线在不同介质中的折射角和反射角。

这些公式对于解决实际问题和设计光学器件具有重要意义。

总之，光的折射公式n1*sinθ1 = n2*sinθ2和光的反射公式θ1 = θ2可以帮助我们计算光线在不同介质中的折射和反射角度。

这些公式是光学研究和实践中的重要工具，对于理解光的传播和光学器件的设计有着重要意义。

第3章几何光学的基本原理(第3讲)

第3章几何光学的基本原理(第3讲)

§3.3 光在球面上的反射和折射
二、球面反射
1. 球面反射对光束单心性的破坏 根据反射定律，
AP PC AP' CP'
s r r s'

l l'
第三章 几何光学的基本原理
1 1 1 s' s l' l r l' l
s’ 的值与l 和 l ’有关，是变量，即球面反射时光束的单 心性受到破坏。
§3.3 光在球面上的反射和折射
第三章 几何光学的基本原理
一、符号法则
1. 球面的几个概念
（1）球面的中心点称为球面的顶点O； （2）C是球面曲率中心； （3）通过C，O的直线称主光轴； （4）通过主光轴的平面称主截面。
（5）r 是球面曲率半径；
2. 新笛卡尔符号法则
（1）轴向距离（物、像、焦距、 曲率半径等）：从顶点 O 算起， 右为正，左为负。
第三章 几何光学的基本原理
3. 焦点与焦距
平行于主光轴的入射光线折射后和主轴相交的交点称 像方焦点F ’，从顶点O到像方焦点的距离称像方焦距f ’。

物空间 O
像空间
F’
F’
f’
虚焦点
实焦点
O -f ’
球面折射成像公式 n' n n'n s' s r
n' 也写成 f '

f ' n' r n'n

0.1m
最后像是处于镜后0.1米处的虚像。
当光线从右至左时，可得到相同结论。
§3.3 光在球面上的反射和折射
第三章 几何光学的基本原理
三、球面折射

光学讲义-几何光学基本公式

光学讲义-几何光学基本公式
19. 针孔照相机的针孔到底片的距离 F = 10cm 。 求：拍摄远处物体时能使像最清晰的针孔直径 D 。波长取 λ = 550nm 。
20. 一侦察卫星的轨道高度 h = 220km ，在可见光波段（取 λ = 550nm ）能分辨地 面上 l = 6.25cm 的间隔。 求：卫星成像系统的孔径（直径） D 。
衍射光栅 光栅：周期分布的全同衍射单元构成的衍射屏。 多缝光栅：
光栅常数 d ：两个相邻衍射单元（如：狭缝）对应位置（如：狭缝中心） 的间距。 光栅公式 d sinθK = Kλ θK ：第 K 级衍射波的衍射角
光学•习题
1. 如图，已知三棱镜的顶角 A 和三棱镜材料的折射率 n 。 求：经过三棱镜的光线的偏向角的最小值。
i
3. 光线入射到玻璃半圆柱的平面上，光线方向与半圆柱 的 轴 垂 直 。 玻 璃 的 折 射 率 n = 1.414 ， 光 线 入 射 角 i = 45D 。 求：光线离开柱面的位置。
4. 一个调节良好的分光计的平行光管和望远镜物镜的焦距分别为 f1 = 250mm 和 f2 = 200mm 。平行光管的狭缝宽度为 b = 1.4mm ，三棱镜顶角为 A = 60D 。 对某两条相邻的谱线，三棱镜材料的折射率分别为 n1 = 1.498 和 n2 = 1.502 。 问：通过望远镜看到的这两条谱线是否重叠？
13. 在成像系统和像面之间插入两个薄透镜，使得在保持像的位置不变的条件下 将像放大，并且放大倍数连续可调。已知两透镜的焦距分别为 f1 和 f2 ，求两 透镜位置间的关系。
14. 在水深 S = 1.0m 的水池有一长度 l = 10cm 的物体。物体经一透镜成像于水面 上 方 H = 80cm 处 的 屏 幕 上 。 已 知 透 镜 焦 距 F = 10cm ， 透 镜 材 料 折 射 率 n = 1.50 ，水的折射率 nw = 1.33 。 求：透镜到水面的距离 h ，以及像的长度 l′ 。

光在球面上的反射和折射

光在球面上的反射和折射

1 1 1 s s ( ) l l r l l
考虑近轴光线,进一步得到
它的成像规律与介质无关．
1 1 2 s s r
s：物距
s：像距
'
C
FF
o
令 令
s ,
得 得
s ,
r f f 2
凹面镜
r f ; 2 r f , 2
因此球面镜物方焦点与像方焦点重合 .
P
O n n’
A
P’
r
C
-s
s’
5 近轴光线下球面折射的物像公式
M O n n’
l s, l s
'
'
P
P’
r
C
-s
s’
n' n n'n n'n 定义光焦度(optical power) ： s' s r r
r 的单位为米时，光焦度的单位称为屈光度(diopter)
n'n r
P
-u
f
-i’ C
u’
P’
Q
n’
r
s’
-s
单个折射面成像系统的笛卡尔符号规则
笛卡尔坐标规则补充
线段
纵向线段 以球面顶点 O 为原点，以入射光线进行 的方向为正方向，建立物空间坐标 s 和像空间坐标 ， 物点坐标为物距，像点坐标为像距 . s 横向线段 以光轴为起点，向上为正向下为负.
n
y
• S
u
O1
R s1 ’
O2
s2 ’ s2
P’
n' n n'n s' s r
(2).
O1面：s1=-2R, r1=+R, n1=1, n1’=1.5

光学 第3章 几何光学的基本原理

光学 第3章 几何光学的基本原理

(1) 偏向角
i1
又
i2
i2
i2 '
i1'i2
A
'
i1 i1' A
(2) 最小偏向角0
当i1改变时 、i1'均随之而改变，当 i1 i1'时，偏向角取最小 0。
0 2i1 A
A
此时在棱镜内传播的光线平行于底边，有:
i2
i2 '
A 2
，i1
i1'
0
2
A
2. 棱镜的折射率
3、折射定律：(1) 折射线在入射线和法线决定的平面内； (2) 折射线、入射线分居法线两侧； (3) 折射角和入射角满足斯涅尔定律：n1sini1=n2sini2
i1 i1'
n1
n2
i2
7 反射和折射定律光路图
3、光的独立传播定律：几个光源发出的光在空间传播并相遇后， 它们将各自保持自己原有的特性(频率、波长、偏振状态)沿原来 的方向继续传播，互不影响。 4、光路可逆原理：当光线的方向反转时，它将逆着同一路径传 播，称为光路可逆原理。
i2 i2
A2 x2,0
i1 i1
B2 n2
x
n1
晰，像的深度由上式确定，y‘ 叫做像似深度 ，y是物的实际深度。
20
(3)像散现象：当i1≠0，即入射光束倾斜入射时，折射光线会发生像散现象。如沿 着倾斜的角度观察水中的物体时，像的清晰度由于像散而被破坏。
例1: 使一束向P点会聚的光在到达P点之前通过一平行玻璃板。如果将玻璃板 垂直于光束的轴竖放，问会聚点将朝哪个方向移动？移动的距离为多少？
A1 A2
P
P'
M

光学教程 第三章

光学教程 第三章

P'
− s'
o
PO = − s PA = l
P' O = − s' AP' = l '
ϕ：半径AC与主轴的夹角
光程PAP′ 为：
∆ PAP ' = nl + nl '
Q cos ϕ = − cos(π − ϕ )
PC = (− s ) − (−r ) = r − s
CP ' = (−r ) − (− s ' ) = s '− r
1. 单心（同心）光束：凡是具有单个顶点的光束
S 发散的同心光束
S 会聚的同心光束 光束的心在无穷远
二. 物和像
1. 物点： 入射到光学系统的单心光束的顶点（P） (1) 实物点：发散的入射单心光束的顶点（P）-----实物 (2) 虚物点：会聚的入射单心光束的顶点（P）-----虚物 2. 像点： 经光学系统出射后又汇聚的单心光束 的顶点（P′） (1) 实像点：会聚的出射单心光束的顶点（ P′ ）-----实像 (2) 虚像点：发散的出射单心光束的顶点（ P′ ）-----虚物
2. 球面的顶点、主轴、主截面
P
Ｃ
o
P'
球面的顶点：一部分球面的中心为O 主轴：连接顶点和曲率中心的直线CO 主截面：通过主轴的平面
3. 符号法则（新迪卡尔符号法则）
（１）线段的长度
纵向线段 以球面顶点O为原点，顶点右为正；左为负 横向线段 以光轴为起点，向上为正，向下为负
（2） 角度 以光轴或法线为始边，沿小于π 的方向旋 转，顺时针为正，逆时针为负．
i
P
−u
Ｃ
o
−s
P'

《光学教程》姚启钧原著-第三章-几何光学的基本原理

《光学教程》姚启钧原著-第三章-几何光学的基本原理

第三章
3.4 光连续在几个球面界面上的折射
子系统1
子系统m
子系统N
物
像
y1 y
y’N y’
一、共轴光具组
1、光轴 (optical axis) ---- 光学系统的对称轴 各球面的球心位于同一条直线上 连接各球心的直线为光轴
共轴光具组
实际成像系统通常由多个折射球面级联构成
r
n
n’
F
F’
O
C
像方焦点F’：与光轴上无穷远处物点对应的像点 像方焦距f’：与像方焦点对应的像距 像方焦平面：过F’点垂直于光轴的平面
像方焦距:
四、球面折射对光束单心性的破坏
物方焦点F : 与光轴上无穷远处像点对应的物点 物方焦距f ：与物方焦点对应的物距。 物方焦平面：过F点垂直于光轴的平面。
1
1’
O
二、几何光学的基本实验定律
1
1’
O
2
（3）光的折射定律
二、几何光学的基本实验定律
（4）光的独立传播定律和光路可逆原理
二、几何光学的基本实验定律
适用条件： R远大于光波长λ （否则，用衍射光学）
二、几何光学的基本实验定律
三、 费马原理
（一）、概念 光程:
B
A
低损耗
玻璃 几千dB/km
石英光纤 0.2 dB/km
2) 信带宽、容量大、速度快
3) 电气绝缘性能好 无感应 无串话
5) 资源丰富 价格低
4) 重量轻 耐火 耐腐蚀 可用在许多恶劣环境下
折射棱镜
四、棱镜
四、棱镜
五脊棱镜
直角棱镜
使像转过900
反射棱镜
： 借助光在棱镜中的全反射，改变光进行的方向.

几何光学的基本原理3.3

几何光学的基本原理3.3
利用几何知识可以得到单球面反射系统成像公式
1 l

1 l

1 r
(
s l

s l
)
考虑近轴光线,进一步得到
1 s
s：物距

1 s

2 r
r：曲率半径
s'：像距
它的成像规律与介质无关．
令 令
s ,
s Байду номын сангаас ,
2 r 得 f , 2
得 f
r
;
f f
r 2
因此球面镜物方焦点与像方焦点重合 . 凹面镜
3.3 光在球面上的反射和折射
1、球面的几个概念 符号法则
球面顶点：O 球面曲率中心：C 球面曲率半径：r 球面主轴(光轴)：连接O、C而得的直线。 主截面：通过主轴的平面。
C
r
O
主轴
光轴 ---光学系统的对称轴
光轴
近轴光线---与光轴夹角较小，并靠近光轴的光线
黄线—近轴光线
绿线—非近轴光线
1. 符号规则(sign convention)
-s = -x-f s’ = x’+f’
xx' ff '
牛顿成像公式
例1、一个折射率为1.5的玻璃球，半径R，置于空气 中。在近轴成像时，问： （1）无穷远处的物成像在何处？ （2）物在球前2R处，成像在何处？
n=1.5
P1’ O2
R s2 ’ s2 s1 ’ P’
P -s1
O1
n=1.5
解：
n' s' n s n' n r
-s1
O1 R
O2 P’ s2 ’ s2 s1 ’

光学教程-总结

光学教程-总结

s in 1
0.61
R
1.22
D
艾里斑的线半径为： l 1.22 f
D
第二章 光的衍射
任何具有空间周期性的衍射屏都可以叫衍射光栅。
I
p
Ap2
s in 2 u2
u
sin2 N(d sin
sin2(d sin )
)
I0
s in 2 u2
u
sin2 Nv sin2 v
第二章 光的衍射
光栅衍射的强度分布 I / I0
B
r s
第三章 几何光学基本原理
近轴光线条件下球面反射的物像公式
1 1 2 s s r
对于r一定的球面，只有一个s
P
和给定的s对应，此时存在确定的像点。
这个像点是一个理想的像点，称为高
斯像点。s称为物距， 称s为 像距
1 1 1 s s f
C P O
这个联系物距和像距的公式称为球面反射物像公式。
人眼的分辨本领是描述人眼刚刚能区分非常靠近的两个物点的能 力的物理量。
瞳孔的分辨极限角为
U0
0.610
R
0.610
555 10 7 cm 0.1cm
3.4 10 4 rad
1
望远镜物镜的分辨极限常以物镜焦平面上刚刚能够分辨开的两个 象点之间的直线距离来表示，这极限值为
y
f 1
1.220
d
/ f
显微镜是用以观察在其物镜第一焦点附近（靠外）的物体的光学
系统。物体经物镜折射后在中间像面上所产生的艾里斑与平行光束 衍射时有几乎同样大小的角半径。
y 0.610
n sin u
第四章 光学仪器的基本原理

球面反射和球面折射成像

球面反射和球面折射成像
所成的像位于球面顶点右边36cm的位置，且是倒立的实像
球面反射成像
一、凹面镜的反射成像
1
2
3
4
5
f
c
F
成像公式
焦距公式
横向放大率
物点在焦点之内，凹面镜成虚像
y
f
l
l’
y’
c
2
1
F
物点在焦点之外，凹面镜成实像
f
c
l
y
l’
y’
1
1
2
2
F
二、凸面镜的反射成像
f
1
2
3
F
y
1
2
1
2
y’
fቤተ መጻሕፍቲ ባይዱ
l
l’
所以成的是缩小正立的虚像，位于镜前右方10 cm处。
解 按题意，l=-30cm，r =30cm，y=10mm
由成像公式可得 cm
二、球面折射成像公式
物方焦距
-
像方焦距
Q
Q´
O
n
n´
r
C
l´
P´
P
y´
y
三、横向放大率
Q
Q´
O
n
n´
r
C
l´
P´
P
y´
y
定义
|β|>1 放大 |β|<1 缩小
β > 0 像正立 β < 0 像倒立
F
F'
四、近轴光线的作图法
共轴球面系统成像（逐次成像）
01
共轴球面系统所成的最终像，可由第一球面所成之像作为第二球面之物、第二球面所成之像作为第三球面之物逐次计算而得。 光学系统的横向放大率为每次球面成像的横向放大率的乘积。

光学教程___第3章_几何光学的基本原理

光学教程___第3章_几何光学的基本原理

i2 ic的光线折射出光纤;i2 ic 的光线在两层介质间多次全
反射从一端传到另一端.
内窥镜、光导通讯……
为了使更大范围内的光束能在纤维中传播，应选择n1和n2的差
值较大的材料去制造光学纤维。
/ 77
20
四.棱镜
主截面：垂直于两界面的截面. 偏向角：出射线与入射线间的夹角.
＝(i1-i2 )+(i1 -i2 )= i1 +i1 -A
由P点所发出的单心光束经球面反射后，单心性被破坏
/ 77
26
三、近轴光线条件下球面反射的物像公式
当φ很小时，cosφ 1
l r2 r s2 2 rr s r r s2 s
l' r2 s' r 2 2 r s' r r s' r 2 s'
由:
A
d l
n 2rs rsin 0 P
l
l
-u
i
-i′ l '
-u`
C
P` -s` O
化简有：r l
s
s r l'
0
-r -s
即：1 l'
1 l
1 r
s l'
s l
对一定的球面和发光点P（S一定），不同的入射点对应有不同的S‘。
即：同一个物点所发出的不同光线经球面反射后不再交于一点。
第三章 几何光学的基 本原理
/ 77
1
干涉和衍射现象揭示了光的波动性，所有 光学现象都能够用波动概念解释。但是在波面 线度远大于波长时，研究光的反射，折射成象 等问题，如果不用波长、位相等波动概念而代 之以光线和波面等概念，即用几何的方法来研 究，将更为方便。

几何光学基本定律球面反射和折射成像

几何光学基本定律球面反射和折射成像
几何光学基本定律球面反射和折射成像
P
P
CF
凹面镜： 物距：P>R 像距：R/2(f)<p’<R 倒立缩小实像
P CPF
凹面镜： 物距：f<P<R 像距：p’>R 倒立放大实像
几何光学基本定律球面反射和折射成像
C F P P
凹面镜： 物距：0<P<f: 像距：p’<0 正立放大虚像
P
P F C
凸面镜： 物距：任意值 像距：-f<p’<0 正立缩小虚像
n21
sin i sinr
v1 v2
绝对折射率：一种介质相对于真空的折射率 n c v 。
设
c n1 v1
c n2 v2
n 21
v1 v2
n2 n1
n1sinin2sinr 几何光学基本定律球面反射和折射成像
几种介质的折射率:
介质 金刚石 玻璃 水晶 岩盐
冰
折射率 2.42
1.50 ~ 1.75 1.54 ~ 1.56
发散光入射凸面镜： 总是成虚像 P
几何光学基本定律球面反射和折射成像
R
P
C
符号法则：
物点 P 在镜前时，物距为正；物点 P 在镜后 时，物距为负。
像点在镜前时，像距为正；像点在镜后时， 像距为负。
凹面镜的曲率半径 R 取正，凸面镜的曲率半 径 R 取负。
实正虚负!
几何光学基本定律球面反射和折射成像
i i
几何光学基本定律球面反射和折射成像
11-1-3 光的折射
折射定律： ⑴ 折射光线总是位于入射面内， 并且与入射光线分居在法线的两 侧；
i i v1 n1
n2
r v2

[理学]《光学教程》姚启钧第三章几何光学的基本原理

[理学]《光学教程》姚启钧第三章几何光学的基本原理
(a) 原理
光学纤维:中央折射率 大,表层折射率小的透 明细玻璃丝.
光进入光学纤维后,多次 在内壁上发生全内反射, 光从纤维的一端传向另 一端.
n
n
r
a 阶跃型光纤 b
r
梯度型光纤
阶跃型多模光纤
梯度型多模光纤
2 i
阶跃光学纤维的端面
n0
B A
n2
n2 n1
i
i
n1
n2
2 n12 n2 )
2、焦点与焦距
F 和物方焦距 f 物方焦点
F
F
f
f
将s f，s 代入(3)式，可得
f
透
n1
（5）
薄透镜物像距公式

n2 n1 n n1 n2 n 透 （3） s s r r2 1 F 和像方焦距 f 像方焦点
F
F
f
f
将s ，s f
代入(3)式，可得
f
透
f n 2 0 f n1
n2
（6）
由（ 5）、（ 6）式可知：
结论：物方焦点和像方焦点肯定在透镜的两侧。
三、高斯公式
将焦距公式（5）、（6）代入物像距公式（3）中，可得
高斯公式：
f f 1 s s
o
f
f
F
（7）
P
F
P
s
s
1 1 1 当n1 n2时，有 s s f
错：
（8）
f f 1 s s
1 1 1 s s f
四、垂轴放大率
Q
y P
①
三棱镜
三棱镜两折射面的夹角称三棱镜顶角A。 出射光与入射光之间的夹角称棱镜的偏向角。

关于球面折射物象公式的两种推导

关于球面折射物象公式的两种推导

关于球面折射物象公式的两种推导作者：汤慧娟来源：《时代教育·下半月》2013年第10期摘要：本文分别用三角函数、几何方法两种方式推导出近轴光线条件下球面折射的物象公式，并对各种推导方法进行比较。

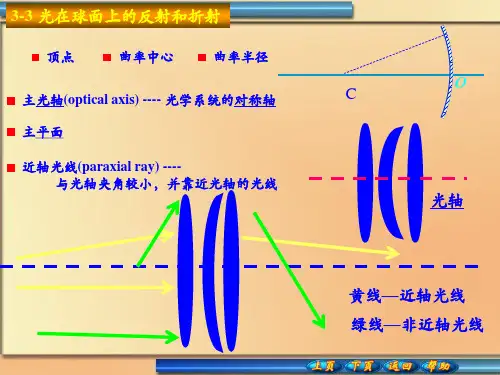
关键词：球面折射物象公式近轴光线中图分类号：G712 文献标识码：C DOI：10.3969/j.issn.1672-8181.2013.10.0331 引言球面折射成像知识在几何光学成像理论中占有举足轻重的地位。

课本上任意多个球面成像即理想光具组问题的求解常常是利用单球面折射成像公式，然后在使用逐次成像法来解答。

任何的涉及到基础光学的书籍中都有球面折射物象公式的推导。

对于球面折射的球面物象公式，大多数书籍都是由费马原理出发逐步推导出来的，有的则是将折射定律与几何知识相结合导出其公式的。

下文将从三角函数和几何方法出发推导出近轴光线条件下球面折射的物象公式。

2 从三角函数出发推导球面折射物象公式下图1中，n、n'分别表示两种不同媒质的折射率，r表示分界面曲率半径，o表示入射光线与主光轴之间产生的夹角，与分界面交于A点，A点距主光轴距离为h，分析物距-s，象距s'的关系[1]。

由折射定律nsinα=n'sinβ （1）（3）式为非近轴条件下单球面折射成像的精确公式在近轴条件下△≈0 h≈0（3）式化为[[n（s-r）s]=[n'（s'-r）s']]化简得近轴条件下折射物象公式[[n's']-[ns]=[n'-nr]]3 从几何方法出发推导球面折射物象公式几何光学中描述光线只需两个量，即光线和光轴的夹角及光线在某些关键点离开光轴的高度[1]。

图2中，设光线射到球形折射面的方向为-θ，到达球面折射面时高度为h。

可记为（-θ，h），此光线折射后偏折角为α-β。

在近轴条件下，s]，近似的折射定为nα≈n'β，所以光线偏折角写为光线（-θ，h）在均匀介质中行进l后（沿光轴方向计量），高度增加l（-θ）.即h➝h+l（-θ）（5）（8）（9）为近轴几何基础，光线（θ，0）从P出发，到达折射面时为高这光线继续行进s'后，高度变为零，即4 结论本文在运用三角函数推导球面折射物象公式[2]时，是先推导非近轴条件下的物象公式，然后按照近轴近似得出近轴条件下物象公式。

球面反射公式

球面反射公式

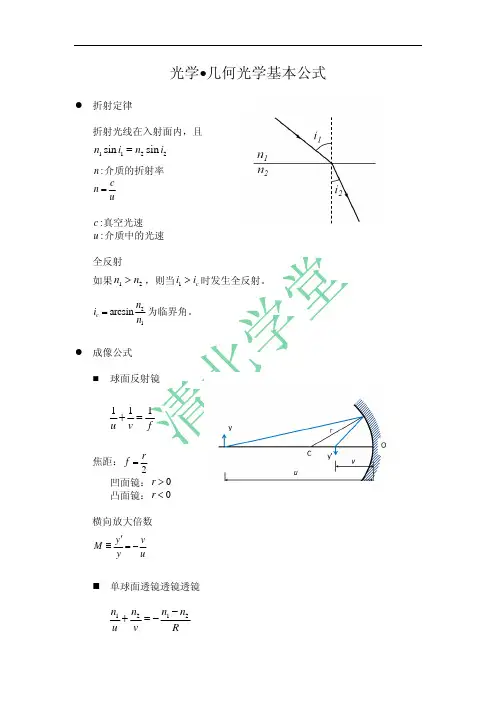
球面反射公式
球面反射公式是用于描述光线经过球面反射后的路径和角度变化的数学关系。

它是光学中重要的基本原理之一，应用广泛。

根据球面反射公式，当入射光线经过球面的表面反射时，反射光线的入射角度（i）和反射角度（r）之间存在一个特定的关系。

这个关系可以用下面的公式来表示：
sin(i)/sin(r) = n2/n1
其中，sin(i)是入射角的正弦值，sin(r)是反射角的正弦值，n1是入射介质的折射率，n2是反射介质的折射率。

折射率是描述介质对光的折射能力的物理量，它与介质的光密度有关。

通过球面反射公式，我们可以计算出光线经过球面反射后的出射角度，从而预测光线在球面上的传播路径。

这在设计眼镜、摄像机镜头等光学设备时非常有用。

需要注意的是，球面反射公式仅适用于球心位于入射光线所在直线上的球面反射情况。

对于球心不在入射光线所在直线上的情况，我们需要使用更复杂的几何光学理论来求解。

总结一下，球面反射公式是描述光线经过球面反射后的角度变化关系的重要公式。

它在光学领域的应用十分广泛，对于设计光学设备和理解光的传播具有重要意义。

代入单球面折射成像公式

代入单球面折射成像公式
法线
Ｃ
Ｆ 实像
虚物
（2） =－1/4 ，则


ns ns


s，s

1 4
即 s＝4s．这说明物像位于凹面镜的同侧．由于物
像之间距离为1000毫米，故可得出像距|s|=333.3毫
米． 若以s=333.3毫米，s=1333.3毫米代入，则得r0，
不合题意．
若用s=-333.3毫米， s=-1333.3毫米代入，可 求得凹面镜的曲率半径为r=-533.3毫米．此种情 况是实物成实像。
r
n2 n1 n n1 n2 n
s' s r1
r2
n n1 n2 n
r1
r2
焦
距
f ' n'r n'n
f nr n'n
f ' f r 2
f ' n2 f n1


单球面折射 高斯公式 f ' f 1
s' s
单球面反射 11 1 s' s f '
薄透镜
f ' f 1 s' s
牛顿公式 xx' ff ' xx' f 2
xx' ff '
横向放大率 ns'
n' s
s'
s
n1s'
n2 s
x' f
f' x
3. 空气中的薄透镜（n1＝n2＝1）
11 1
物象关系

s' s f '
光焦度
焦距
第二种情况的光路图如下
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例3.4:
一个折射率为1.6的玻璃哑铃，长20cm，两端的曲率半径为 2cm。若在 离哑铃左端5cm处的轴上有一物点,试求像的位置和性质。
[解]：两次折射成像问题。
n
P
O1
n
P’1 n` O 2
1、P为物, 对球面O1折射成像P1’
已知 : s1 5cm , r1 2cm , n 1, n ' 1.6 n n n n 由折射成像公式 ' r1 s1 s1
沿轴线段
A、凡光线与主轴交点在顶点右方者线段长度数值为正； 凡光线与主 轴交点在顶点左方者线段长度数值为负； B、物点或像点至主轴的距离在主轴上方为正，下方为负。 ② 光线的倾角均从主轴或球面法线算起，并取小于900的角度；由主轴 （或法线）转向有关光线时： A、顺时针转动，角度为正；B、逆时针转动，角度为负。 （注意：角度的正负与构成它的线段的正负无关）
2
r
2
s r
'


2
2 r s ' r cos


光程 PAP ' nl nl ' n
r 2 r s 2 2 r r s cos r

2
n
s r
'


2
2 r s r cos
1、高斯公式：

球面反射 : f ' f 1 1 2 ' s s r
六、理想成象的两个普适公式
n' n n' n 将物像公式 ' 变形为 : s s r n' n r r ' ' ' f f n n n n 1 1 ' ' s s s s
高斯公式
对任何理想成像 过程均适用
n' n n' n f ' f 在 球 面 折 射 中, ' , ' 1, xx ' ff '三 者 等 效 ; s s r s s
② 高斯公式、牛顿公式是近轴条件下理想成像的普适公式。 只是在不同情况下，焦距的形式不同而已。 r 1 1 2 高斯公式 ' 如 : 球面反射 f f ' 2 s s r
' 焦距：焦点到球面顶点的距离（f
C
F` -r
f
'
P` -s` O
-s
r ）。它同样遵守符号法则。 2

1 1 1 s' s f'
说明：1、它是球面反射成像的基本公式，只在近轴条件下成立； 2、式中各量必须严格遵从符号法则； 3、对凸球面反射同样适用； 4、当光线从右至左时同样适用。
2、牛顿公式： 若将取值原点由顶点O改 为物、像方焦点F、F’，则 有如下关系（如右图示）
n
P
n`
F
x
f
O
r
f
C
P`
F' ' x
s`
牛顿公式
对任何理 想成像过 程均适用
sf x
s' f ' x'
'
-s
则高斯公式变为 :
3、说明： ①
f f ' ' 1 化简可得 : xx ff f ' x' f x
设n<n’
P`
-s
s`
在 PAC 和 ACP '中,由余弦定理有 : l l
'
r 2 r s 2 r r s cos
2
r s r
2 '


2
2 r s ' r cos


光程 PAP ' nl n 'l ' n r r s 2 r r s cos
垂轴线段
③ 图中出现的长度和角度只用正值。符号按 照新笛卡尔法则额外加入。 例：球面反射成像各量的正负。 无论光线从左至右还是从右至 左，无论是球面反射还是折射， 以上符号法则均适用。 以下的讨论假设光线从左至右进行。
A
l
P -u C

i
-r
' l -i`
-u` P` -s` O
-s
对l , l ' , 不适用 !!
三、近轴光线下球面反射的物像公式
1、近轴光线条件
当 很小时, cos 1 l l
'
r 2 r s 2 2 r r s r r s 2 r
2
s
2
s r
'


2
2 r s r
-s O
s`
最后像是处于镜后0.1米处的虚像。 当光线从右至左时，可得到相同结论。说明符号法则均适用
四、球面折射对光束单心性的破坏 -i A 1 n n` ' l -i2 l 从主轴上P点发出单心光 -u u` 束，其中一条光线在球面 O C r P 上A点折射，折射光与主
轴交于P`点。即P`为P的 像。
A、像方焦点 F’、像方焦距
f
''Fra biblioteknn n -s
'
n`
O
F`
当 s 时,由物像公式 得:
' n f ' s' ' r n n
n n ' s s
r
s’ f`
n
B、物方焦点F、物方焦距
'
f
F
n`
O
n' n n' n 当 s 时,由物像公式 ' s s r n 得: f s ' r n n ' f' n' f • ∵ n n C、 f n
'


A
对给定的物点，不同的入射点，对
l
P -u
C
应着不同的入射线和反射线，对应
着不同的 。
由费马原理可知 : 当
d PAP ' d
0 时,
i -i` l ' -u` P` -s` O -r
PAP ' 取得极值(此处是恒定值). 由 d PAP ' d
-s
n 2r r s sin n' 2r s ' r sin 0 l l
二、球面反射对单心性的破坏
从主轴上P点发出单心光束，其中一条光线在球面上A点反射，反射光与 主轴交于P`点。即P`为P的像。 按符号法则，各有关线段和角度的正负如图所示。s — 物距 s`— 象距
在 PAC 和 ACP '中,由余弦定理有 : l l
'
r
2
r s 2 r r s cos
' '
P2 ‘
-s1
s1 ’ -s2’
-s2
得 : s1'
n'
n' n n r s 1 1
代入数据 16cm
已知 : s2 20 16 4cm, r2 2cm, n 1.6, n ' 1 同1有 : s
' 2
2、P1
’为物,
对球面O2折射成像
也可用高斯公 式、牛顿公式 求解！
n'
n n n r s 2 2
'
代入数据 10cm
§3-4
光连续在几个球面上的折射
虚物
实际的光学系统大多由两个或两个以上的球面所构成。研究多个 球面上的折射成像更具实际意义。
一、共轴光具组



r s s' r 1 1 1 s' s 化简有 : 0 即: ' ' ' l l l l rl l 对一定的球面和发光点P（s一定），不同的入射点对应有不同的s’。 即：同一个物点所发出的不同光线经球面反射后不再交于一点。
由P点所发出的单心光束经球面反射后，单心性被破坏
§3-3
1、基本概念：
光在球面介面上的反射和折射
符号法则 r O 主轴
一、球面的几个概念
球面顶点：O 球面曲率中心：C C 球面曲率半径：r 球面主轴：连接O、C而得的直线。 主截面：通过主轴的平面。
2、符号法则：为使计算结果普遍适用，对线段和角度正负取法的规定。
① 线段长度均从顶点算起： 新笛卡尔法则
物空间
像空间 S’>0:实像 物空间 像空间
n P
物空间 像空间
n` s` P`
S’<0:虚像 物空间
n
P P` -s` O -s n`
虚像在物空 间,但实际 存在的是像 空间的发散 光束,故像 方折射率仍 为n’.
-s O
P
-s
S’<0:实像
P` -s` O
像空间
P -s
s’ P’
S’>0:虚像
⑥ 焦点、焦距
2 2
n
'
r s r
2 '


2
2 r s ' r cos


n
对给定的物点，不同的入射点，对 应着不同的入射线和折射线，对应 着不同的
l
-i1 A

P
-u -s
-i2
l'
n` P`
O