当前位置：文档之家 › 正切函数的性质和图象

正切函数的性质和图象

  • 格式：doc
  • 大小：123.50 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

知识讲解正切函数的性质和图象基础

知识讲解正切函数的性质和图象基础

知识讲解_正切函数的性质和图象_基础正切函数是三角函数中的一种，常用符号为tan，表示一个角的正切值。

在数学中，正切函数具有许多重要的性质和图像，下面将对其进行详细介绍。

1.定义：正切函数的定义是：对于一个角θ，它的正切值tanθ等于角的对边与邻边的比值，即tanθ=opposite/adjacent。

2.周期性：正切函数具有周期性，即tan(θ+π)=tanθ，其中π是圆周率。

这意味着正切函数的图像在每个周期内重复出现，以直线y=tanθ为对称轴。

3.定义域和值域：正切函数的定义域是所有实数，除了使分母为零的角度。

当角度为90°的倍数时，分母为零，正切函数无定义。

正切函数的值域是所有实数，即从负无穷到正无穷。

4.奇偶性：正切函数是一个奇函数，即tan(-θ)=-tanθ。

这意味着正切函数的图像关于原点对称。

5.渐近线：正切函数有两条渐近线，分别为x=π/2+kπ和x=-π/2+kπ，其中k是整数。

当θ接近这些值时，tanθ的值趋向于正无穷或负无穷。

6.零点：正切函数有无数个零点，即tanθ=0。

这些零点出现在角度为kπ时，其中k是整数。

7.图像变换：对于正切函数的图像，可以通过平移、缩放和反转等变换得到。

例如，将y=tanθ的图像向右平移π/4个单位，得到y=tan(θ-π/4)的图像；将y=tanθ的图像进行垂直缩放，得到y=a*tanθ的图像，其中a 是一个常数。

8.切线斜率：正切函数在每个周期内都有无穷多个切线，切线的斜率是tanθ。

这意味着切线的斜率在整个图像上是连续变化的。

9.函数图像：正切函数的图像是一个周期为π的波浪线。

在每个周期内，图像从负无穷逐渐上升到正无穷，然后再从正无穷逐渐下降到负无穷。

图像在每个周期内有一个零点，并且在每个周期的中点有一个峰值和一个谷值。

总结起来，正切函数是一个周期性的、奇函数，定义域为所有实数，值域为所有实数。

它具有两条渐近线，有无数个零点，图像是一个波浪线，切线的斜率等于函数值。

正切函数的图像和性质最新版

正切函数的图像和性质最新版

学习过程
1、画出正切函数在一个周期


2
， 2

内的图象
y

0

x
2
2
§1.4.3 正切函数的性质和图象
1.正切函数 y tanx的性质：
y ytanx
定义域： {x|xk,kZ}
2
值域： R
周期性： 正切函数是周期函数，
周期是

2
奇偶性： 奇函数 tan(－x)=－tanx
§1.4.3 正切函数的图象和性质 （一）
1、利用正切函数的定义，说出正切函数的定义域；
tan y x0 的 终 边 不 在 y 轴 上
kx kz
2
2、利用周期函数的定义及诱导公式，推导正切函数 的最小正周期；
tan(x)tanx 是 ytanx的 周 期 ；
单调性： 在 (k,k) kZ
22 内是增函数
对称性： 对称中心是(k ,0), k Z
2


2
o 2
对称轴呢？
x 2
典型例题
例题1
解：
比较 tan ( 1 3 ) 与 tan ( 1 7 ) 的大小.
4
5
tan134tan4 tan175tan25
典型例题
例题2
讨论函数
y

tan

x


4

的性质；
1、定义域
x x|xR且 xk4， kZ
2、值域
y R
3、单调性
4、奇偶性
在 x k3 4 ,k 4 上 是 增 函 数 ；
f(x)tan(x)tan(x)f(x)

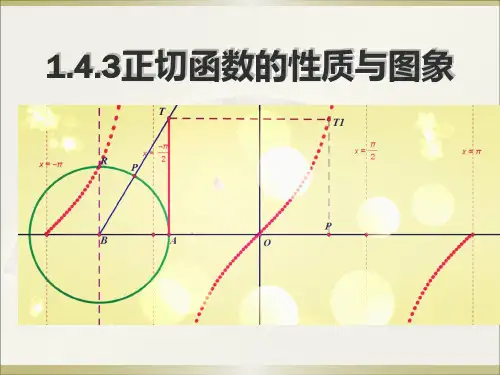
正切函数的图像和性质 (精致版)

正切函数的图像和性质 (精致版)
奇函数 偶函数
2 对称轴： x k , k Z
2 对称中心： (k ,0) k Z
2
对称轴： x k , k Z 对称中心：( k , 0) k Z
2
探索一 你可以从一个新的角度来研究正 切函数的性质吗？
正弦函数 正切函数
定义+三角函数线
三角函数图象
课后练习

作业：
P45.2、3、4
课后思考

思考1：我们分别从什么角度讨论了正切函数 的性质？这两种讨论方法分别有什么特点？ 思考2：你能用同样的方法去讨论正、余弦 函数的性质吗？

想一想？ 得到y tan x最小正周期为__ ____
由y tan x最小正周期为
反馈练习：求下列函数的周期：

x (1) y 5 tan 2
2

(2) y tan(4 x ) 3

4
巩固练习 1、比较下列每组数的大小。
13π 11π tan() 与 tan() （2） 4 5
正切函数的对称中心
正 切 函 数 图 像
性质 :
渐 进 线
渐 进 线
⑴ ⑵ ⑶ ⑷
定义域： {x | x k, k Z} 2 值域： R 周期性： 奇偶性： 奇函数，图象关于原点对称。
⑸ 单调性： 在每一个开区间 ( k , k ) ， k Z 内都是增函数。 2 2 kZ x k , (7)对称中心 (6)渐近线方程： 2
kπ ( ,0) 2
问题：
(1)正切函数是整个定义域上的增函数吗？为什么？
(2)正切函数会不会在某一区间内是减函数？为什么？
A
B

1.4.3正切函数的图象与性质

1.4.3正切函数的图象与性质

x 变式题：求函数y 3 tan(- )的单调区间. 2 4 x
4 3 （2k ， 2k ），k Z . 2 2
y 3 tan(-
3 2k - x 2k ,k Z 2 2 x
2
)的单调递减区间为 :
1、函数y tan( x A.{ x R | x k

4
)的周期是（ C ）

C、 3

D、 6

课堂练习
３、直线y=a（a为常数）与正切曲线y=tanx 相交的 相邻两点间的距离是( A )
A、
B、/2
C、2
D、与a值有关
4、与函数y tan( 2 x 一条直线是（ D） A. x

4
)的图象不相交的

2
B. x -

2
C.x

4
D. x

8
课堂练习 课本P45 练习2
3 2
y


y tan x
1


2
-1
0
2
3 2
x
观察正切曲线，写出满足下列条件的x的值的范围：
(1) tan x 0
(2) tan x 0
︱ k x k , k Z} {x 2 {x︱ x k , k Z }
（2）
3 (0, ) ( , ) 4 4
课本P45 小(1)tan138与tan143
课堂练习 练习6 比较下列各组是两个正切值的大
思想：在同一个单调区间比较！
13 17 (2) tan 与 tan 4 5 (1) 90 138 143 270 tan 138 tan 143 13 17 2 (2) tan tan , tan tan 4 4 5 5 2 且 0 2 5 4 2 17 13 tan tan tan tan 5 4 5 4

正切函数的性质与图象 课件(34张)

正切函数的性质与图象 课件(34张)
提示:奇偶性.
数学
[问题1-4] 结合正切函数的图象.你能判断一下它的单调性吗?




提示:在每一个开区间(- +kπ, +kπ)(k∈Z)上都单调递增.
梳理
正切函数y=tan x的性质与图象
y=tan x
图象
数学

定义域
{x|x∈R,且 x≠kπ+ ,k∈Z}

R .
值域
周期
最小正周期为 π .
奇偶性
奇函数 .
单调性
在开区间




(kπ- ,kπ+ )(k∈Z)
内递增
数学
小试身手
1.函数 y=tan 2x 的周期为( A
)

(A)

(B)π
(C)2π
(D)4π

解析:由题意可知,函数 y=tan 2x 的周期为 T= .故选 A.

数学
2.函数 f(x)=3tan(x+π)是( A
)




x 的范围即可.②若ω<0,可利用诱导公式先把 y=Atan(ωx+ )中 x 的系
数化为正值,再利用“整体代换”的思想,求得 x 的取值范围即可.
(2)比较正切值的大小
第一步:运用学过的三角函数的周期和诱导公式将角化到同一单调区
间上;
第二步:运用正切函数的单调性比较大小关系.
数学
备用例题
数学
5.4.3
正切函数的性质与图象
数学
核心知识目标
核心素养目标
1.了解正切函数图象的画法,理解
通过利用正切函数的图象与性质

正切函数的图象及性质

正切函数的图象及性质

11 6
●
2
●
2
0
6
3
2
2 3
5 6

● ● ● ● ●
x
3 2
-1
现在利用正切线画出函 数y tan x, x (

y
, )的图象 2 2


1


o1


2


4

0
1

4

2
x

利用正切函数的周期性,把图象向左,右扩展,得到正切函数 y tan x, x R且x k , (k Z )的图象 , 并把它 叫做正切曲线. 2 y
（2） y tan x 性质: 定义域
值 周 奇 域 期 偶 性 奇 R 函 数
单调增区间
对 称 中心
渐近线 方程
x x k ，k Z 2
k， x k 0 k ，k 2 2 2 k Z k Z k Z
2
正切函数的主要性质如下:
定义域 值 域 周期性 奇偶性 单调性
xx

2 k , k Z

实数集
T
奇函数(正切曲线关于原点对称)
在（

k， k），k Z内为增函数 2 2

例1.求函数 y tan x ）的定义域 , 周期和单调区间。 （ 4
解：令 z x
y
解：
3 2


2
0
2

3 2
x
(1). x (k

2
, k ), (k Z )

高一数学正切函数的图象和性质

高一数学正切函数的图象和性质
正切函数 y tan x 的图象和性质：
（1） 定义域
正切函数的定义域：
{x | x

2
k , k Z }
。遇到有关正切函数问题时，
你注意到正切函数的定义域了吗？ （2） 值域 正切函数的值域是 R，在上面定义域上无最大值也无最小值； （3） 周期性 正切函数是周期函数且周期是 ，它与直线 y a 的两个相邻交点之 间的距离是一个周期 。绝对值或平方对三角函数周期性的影响： 一般说来，某一周期函数解析式加绝对值或平方，其周期性是：弦 减半、切不变．既为周期函数又是偶函数的函数自变量加绝对值， 其周期性不变，其它不定。 如 y sin
y sin x cos x
2
x, y sin x
的周期都是 , 但
1 y | 2sin(3x ) |, y | 2sin(3x ) 2 | 6 2 6 的周期为 2 ，而 ，
y | tan x | 的周期不变；
ቤተ መጻሕፍቲ ባይዱ
（4）奇偶性与对称性
k ,0 k Z 正切函数是奇函数，对称中心是 2 ，特别提醒：正(余)切
型函数的对称中心有两类：一类是图象与 x 轴的交点，另一类是渐近 线与 x 轴的交点，但无对称轴，这是与正弦、余弦函数的不同之处。
（5）单调性
新浪微博：北京新东方优能中学教育 人人网：新东方优能中学
k , k k Z 2 2 正切函数在开区间 内都是增函数。但要注意在
整个定义域上不具有单调性。
新浪微博：北京新东方优能中学教育 人人网：新东方优能中学

正切函数的图象及性质

正切函数的图象及性质
⑴ 定义域： {x | x k, k Z} 2 ⑵ 值域： R (3)周期性： π 奇函数，图象关于原点对称 ⑷ 奇偶性： ⑸ 单调性： 在每一个开区间
π π (- + kπ, + kπ)， k Z 内都是增函数。 2 2
(6)对称中心:
kπ ( ,0) 2
，没有对称轴
判断下列命题的真假
1. 观察正切函数图像，你能找出关键的点和线吗？ 2.思考如何画正切曲线的简图，并画出. 提示：三点两线
π π 1),(0, 0),( , 1) 三点： ( , 4 4
两线：
π π x ,x 2 2
正 切 函 数 图 像
渐 进 线
渐 进 线
观察正切函数的图像，你能归纳出 y tan x 的性质吗？
因此，函数的定义域是 x x R且x k , k Z , 值域是R 4 y tan t的单调增区间是 - k , k , k Z 2 2
, 则y tan t的定义域为 t t R且t k + , k Z 4 2 x k , x k 4 2 4
答案:
1、定义域 2、值域
3、单调性
4、奇偶性 5、周期性
1 5 x x | x R且x k ，k Z 3 18 yR 1 5 1 在x k , k 上是增函数； 18 3 18 3
非奇非偶函数
最小正周期是

π π x kπ 且x kπ ,k Z 4 2
基础练习
1．关于正切函数 y
tan x , 下列判断不正确的是（B ）
A 是奇函数 B 在整个定义域上是增函数 C 在定义域内无最大值和最小值 D 平行于 x 轴的的直线被正切曲线各支所截线 段相等

正切函数的定义,图像及性质

正切函数的定义,图像及性质
P40 4
sinx tan x, (k为偶数). cosx
tan( x kπ) tan x,
π 其中，x R, x kπ, k Z . 2
kΠ（k∈Z，k≠0）是正切函数的周期，π是它 的最小正周期。
作法如下：
作直角坐标
系，并在直角 坐标系y轴左侧 作单位圆。
y
找横坐标
（把x轴上 2 到 到这一 段分成8等份）
高一（10）班
7.1 正切函数的定义 7.2 正切函数的图像和性质
在直角坐标系中，如果角α满足：那么，角α的 终边与单位圆交于P(a,b),唯一确定比值 b . a y b P(a,b) 根据函数的定义，比值 是角α的函数，我们把它 叫作角α的正切函数，其 中α R，α π kπ (k Z）。
1

把单位圆右
半圆中作出正 切线。

2
1
3
8 4 8
x
找交叉点。 连线。
利用正切函数的周期性,把图像向左、右扩展,得 π 到正切函数 y tan x( x R, x kπ, k Z ) 的图像， 2 称其为正切曲线。 y

3 2



2
0
2

3 2

α在第一象限时：

P
y
o
A(1,0) MP是正弦线 M x
OM是余弦线
M
A x
T
y
T
AT是正切线
y o M A x T P
M P
o
请同学们画出其它象限的 x A 三角函数线
由正弦函数、余弦函数的诱导公式可得：
sin( x kπ ) tan( x kπ ) cos( x kπ ) - sin( x) tan x, (k为奇数), - cos( x)

高二数学正切函数的图像和性质

高二数学正切函数的图像和性质

4
5

tan

4


tan
2
5
,即
tan

13
4


tan

17 5


练习 不查表比较大小：
(1) tan167 与tan173 (2) tan 470 与 tan 822
例题2
x


4

的性质；
练习 讨论函数 y tan 2x 的性质；
§1.4.3 正切函数的图象和性质 （一）
1、利用正切函数的定义，说出正切函数的定义域；
tan y x 0 的终边不在y轴上


x
k


k

z

2
2、利用周期函数的定义及诱导公式，推导正切函数 的最小正周期；
tan( x) tan x 是y tan x的周期；
1、画出正切函数在一个周期



2
，
2

内的图象
y

0

x
2
2
§1.4.3 正切函数的性质和图象
1.正切函数
的性质：
y y tan x
定义域：
值域：
周期性： 正切函数是周期函数，
周期是
2
奇偶性： 奇函数 tan(－x)=－tanx


2
o 2
x 2
单调性： 在 内是增函数
对称性： 对称中心是
对称轴呢？
；宜宾装修公司/ 宜宾装修公司
；
全家人都知道这个说法，在姐姐的心灵深处，樟木箱子早已深深地扎下了根。 光阴似箭，姐姐真的到了谈婚论嫁的时候了

高中数学：正切函数的图象和性质课件

高中数学：正切函数的图象和性质课件

kπ ( ,0) 2
问 题
讨论Leabharlann 问题：(1)正切函数是整个定义域上的增函数吗？为什么？
(2)正切函数会不会在某一区间内是减函数？为什么？
A
B
π π (- + kπ, + kπ) ，k Z 2 2
在每一个开区间 内都是增函数。
基础练习
1．关于正切函数 y
tan x , 下列判断不正确的是（B ）
90 167 173 180
tan167 tan173
0 0
0
y tan x在 ， 上是增函数， 2
说明：比较两个正切值大小，关键是把相 应的角 化到y=tanx的同一单调区间内，再 利用y=tanx的单调递增性解决。
例 2.
求函数y tan( x


反馈演练
1、比较大小： (1)tan138 _____tan143 。 < 13π 17π > (2)tan()_____tan() 4 5 ２、求函数y=tan3x的定义域，值域，单调增 区间。
k 定义域：｛ x\x , k z｝ 3 6 值域： R
0 0
k k 单调递增区间：（ , ） ,k z 6 3 6 3
正切函数的图象和性质
4.10 正切函数的图像和性质 一、引入 如何用正弦线作正弦函数图象呢？
1、用平移正弦线得 y sinx, x [0,2 ]图象.
2、再利用周期性把该段 图象向左、右扩展得到 .
类 比
用正切线作正切函数y=tanx的图象
4.10 正切函数的图像和性质
二、探究用正切线作正切函数图象
3 , A. 4

正切函数的性质与图象

正切函数的性质与图象

f ( x ) tan( x ) tan( x ) tan[ ( x 2) ] f ( x 2) 2 3 2 3 2 3
因此函数的周期为2.带入正切的单调区间可解得函 数得单调区间
5 1 ( 2k , 2k ), k Z 3 3
(1)1 tan x 0;
y 3

(2) tan x 3 0;

4

3
y 1
小结
正切函数的周期性，奇偶
性，单调性，值域.
作业
课本45页练习
4、值域
正切函数的值域是实数 R. 集
举例
π π 例1 求函数y tan ( x )的定义域, 周 2 3 期和单调区间.
解:
x k 2 3 2
即
所以函数的定义域是 由于
1 { x | x 2k , k Z }. 3
1 x 2k , k Z 3
y A sin( x ), x R.( A 0, 0) y A cos(x ), x R.( A 0, 0)
y A tan( x ).( A 0, 0)
T
2
T
例2 求使下列不等式成立的 的集合: x
§ 1.4.3 正切函数的 性质与图象
引入
正切函数:
y tan x , x k , k Z 2
新课
正切函数图像:
FLASH
1、周期性
正切函数是周期函数, 周期是π.
2、奇偶性
正切函数是奇函数.
3、单调性
π π 在每一个开区间 , kπ ), k Z上都是增函数 (kπ . 2 2

正切函数的图像和性质

正切函数的图像和性质
【错解】π3
（1）正切函数的图像：
（2）正切函数的性质：
定义域：x
|
x

2

k
,
k

Z

值域：全体实数R
周期性：正切函数是周期函数，
最小正周期为

奇偶性：奇函数，
单调性：正切函数在开区间 k, k ,k Z
2 2
内都是增函数。
本节课学习了哪一种数学方法解 题？
利用正切函数单调性比较大小
3．tan 1°与tan 1从小到大的关系是 ________．
【答案】tan 1°＜tan 1
比较正切值的大小
【例 2】 比较 tan－147π与 tan－252π的大小． 【解题探究】利用诱导公式化简函数的表达式，自变量在 正切函数的同一个单调区间内，即可判断大小．

B.xx∈R且x≠kπ＋4π，k∈Z

C.xx∈R且x≠kπ＋2π，k∈Z

D.xx∈R且x≠kπ－4π，k∈Z

【答案】A
例6
（2）周期性
y tan x
2 3
利用正切函数图像解不等式问题
课本P46 A 9 (1) 1 tan x 0
方法（1）在



2
,

2

内找到相应的范围
（2）在两边加上 k
利用几何画板探究 资料书P26 4 例3.求下列函数的周期.
(2)y tan x
3


3
2
2

2
资料书P26例题
3．函数 y＝|tan 2x|是( )
ห้องสมุดไป่ตู้

11 正切函数图像性质

11 正切函数图像性质
1 2 x
4

4
1 k x k 2 2 4 2
:
y 3 tan( 1 2 x
)的单调递增区间为

4
)的单调递减区间为
:
(2 k
3 2
,2 k

2
)
(2 k

2
,2 k
3 2
)
例4 求下列函数的周期：
(1) y 3 tan( 2 x


4
);
:
:
令u
k

2
u k

2
x 2


4
; 所以 y tan u 的单调递增区间为
,k Z
由 u
1 2
x

4
k

得:
u k , k Z 2 2
1 2 x

由 u

得:
k
y 3 tan(

1 x k 2 2 4 2
x k , k x k ， tan x 2 2
（3）周期性：T=π； （4）奇偶性：tan(－x)=－tanx,
∴正切函数是奇函数。
k 对称性：关于（ , 0) 2
中心对称，无对称轴
（5）单调性：
在开区间 k , k k z 2 2
例3 求下列的单调区间：
(1) y 3 tan(
解 : (1) 令 u
u 1 2 x
1 2
x

4

4
);
变题 ( 2 ) y 3 tan(
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1.4.3正切函数的性质和图象
荥阳市第二高级中学
王青琴
【学习目标】
1.通过预习，能根据正切函数定义，诱导公式，正切线从“数”的角度，推出正切函数性质；
2.通过师生合作,能根据正切函数的性质与正切线，画出正切函数的图象；
3.通过师生合作，能根据正切函数的图象和性质解决相关问题。

【学习重点】
1.正切函数的图象与性质；
2.利用正切函数图象与性质解决问题
【学习难点】
利用正切线研究正切函数的单调性及值域
【学习方法】 自主探究 合作交流
【学习思想】类比、数形结合、整体代换、转化
【学习过程】
一、温故知新
1、正切的定义式是什么？
即：角a 的终边不能落在 y 轴上
即：使的集合为有意义的角tan αα
.
2、正弦，弦函数的相关性质有哪些？
思考？正切函数y=tanx 是否有这样的性质呢？
二、新知探究 探究1：根据正切函数定义，诱导公式，正切线推导正切函数的相关性质。

问题1.正切函数的定义域是什么？
结论：正切函数定义域为： .
问题2、你能根据诱导公式，判断正切函数是不是周期函数吗？
结论：正切函数的最小正周期为 .
问题3、你能根据诱导公式，判断正切函数的奇偶性吗？
结论：正切函数为 函数
问题4.你能利用正切线，研究正切函数在一个周期内 的单调性吗？
y =tanx y =tanx ππ(-,)22)0(tan ≠=x x
y α
结论：
问题5. 观察正切线：当x 大于2π
-且无限接近2π
-时，正切值如何变化？
当x 小于2π且无限接近2π
时, 正切值又如何变化？
结论：正切函数的值域是___________
探究2：利用正切线做出正切函数的图象.
问题1. 类比正弦函数图象画法，你能利用正切线，画出y=tanx 在 内的图象吗？
问题2. 根据正切函数周期性，你能画出在其整个定义域内的图象吗？
利用正切线作tan y x =，x ∈⎪⎭
⎫ ⎝⎛-2,2ππ的图象
思考？
正切函数是整个定义域上的增函数吗？为什么？
三、利用性质解题
例题1.求函数)3
2tan(ππ+=x y 的定义域、周期和单调区间。

⎪⎭⎫ ⎝⎛-2,2ππ
变式训练：
小结：性。

的定义域，周期，单调)tan(的数学思想求_____运用ϕ+=wx A y
例题2：比较 138tan 与 143tan 的大小
变式训练： 大小5
17tan 与413tan
比较ππ
求函数 的定义域,周期，单调区间． ⎪⎪⎭⎫ ⎝⎛-=42tan 3πx y
小结：比较两正切值大小的方法
（1）运用三角函数的 将角转化到同一单调区间内；
（2）运用 比较大小关系。

【课堂达标训练】
1、下列函数中,同时满足(1)在(0, 2
π)上递增,(2)以2π为周期,(3)是奇函数的是 ( ) (A)x y tan = (B)x y cos = (C)x
y 21tan = (D)x y tan -= 2、函数)4tan(
x y -=π的定义域为 ( ) (A)},4|{R x x x ∈≠π
(B)},4|{R x x x ∈-≠π
(C)},,4|{Z k R x k x x ∈∈+≠π
π (D)},,43|{Z k R x k x x ∈∈+
≠ππ 3、函数)4tan(x y -=π
的递减区间是
四、课堂小结与收获
1.正切函数的性质：
定义域： 值域： 周期性： 奇偶性：
单调性：
2.数学思想方法： ， ， ，
五、布置作业
1.必做题：课本习题A 组第6题、第8题。

2.选做题：课本习题B 组第2题.
六、拓展延伸
1.（1）求函数y ＝2tan x 1
－的定义域
（2）函数y =的定义域为 .
2.类比正弦函数，你能得到)tan(ϕ+=
wx A y 的周期公式为
对称中心是
七、课后反思。