缀板式格构柱计算

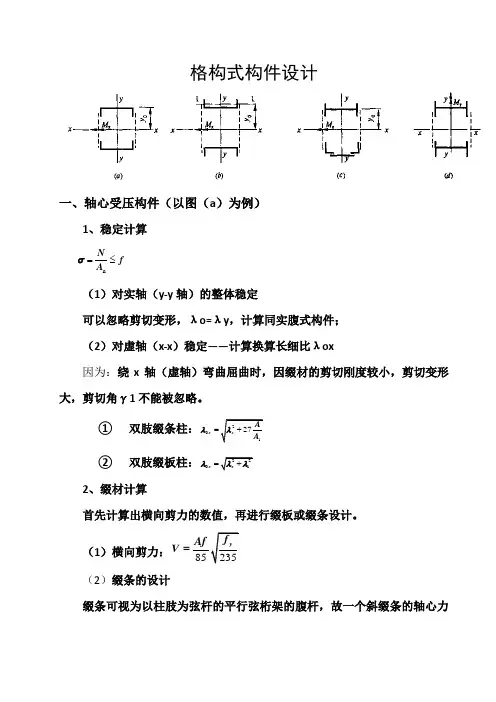
格构式构件设计一、轴心受压构件（以图（a ）为例）1、稳定计算nN f A σ=≤ （1）对实轴（y-y 轴）的整体稳定可以忽略剪切变形，λo=λy ，计算同实腹式构件；（2）对虚轴（x-x ）稳定——计算换算长细比λox因为：绕x 轴（虚轴）弯曲屈曲时，因缀材的剪切刚度较小，剪切变形大，剪切角γ1不能被忽略。

① 双肢缀条柱：20127x x A A λλ=+② 双肢缀板柱：2201x x λλλ+2、缀材计算首先计算出横向剪力的数值，再进行缀板或缀条设计。

（1）横向剪力：85235yf Af V =（2）缀条的设计缀条可视为以柱肢为弦杆的平行弦桁架的腹杆，故一个斜缀条的轴心力为：cos V N n θ=11 （3）缀板的设计缀板柱可视为一多层框架。

当整体挠曲时，假定各层分肢和缀板中点为反弯点。

1111/2/2T V l a M Ta V l =⎧⎨==⎩二、压弯压构件计算1、稳定计算（1）压弯格构柱弯矩作用绕虚轴x 时的整体稳定计算①弯矩作用平面内虚轴x 稳定不考虑塑性性发展系数mx x 1x x E(1)x x M N f N A W N βϕϕ⋅+≤-' ②弯矩作用平面外实轴y 稳定因为平面外弯曲刚度大于平面内（实轴），故整体稳定不必验算，但要进行分肢稳定验算。

③分肢稳定验算将缀条柱视为一平行弦桁架，分肢为弦杆，缀条为腹杆，则由内力平衡求解：212x M N y N a a N N N ⋅⎧=+⎪⎨⎪=-⎩112分肢：分肢：分肢按轴心受压构件（N 1、N 2）计算。

（2）压弯格构柱弯矩绕实轴作用时的整体稳定计算由于其受力性能与实腹式压弯构件相同，故其平面内、平面外的整体稳定计算均与实腹式压弯构件相同，但在计算弯矩作用平面外的整体稳定时，构件的长细比取换算长细比，φb ＝1.0。

（3）双向受弯格构式压弯构件的整体稳定计算1、整体稳定ty y mx x x 1y 1x x E(1)x M M N f N A W W N ββϕϕ++≤-'2、分肢稳定按实腹式压弯构件计算，分肢内力为：212x y y y y y y y y M N y N a aI y M M I y I y N N N M M M ⋅=+=⋅+=-=-111112212112分肢：分肢：。

格构柱受力计算书-CAL-FENGHAI.-(YICAI)-Company One1格构柱受力计算书计算依据：(1)《钢结构设计规范》(GB50017-2003)。

(2)《钢结构设计与计算》1. 格构柱截面的力学特性：格构柱的截面尺寸为×；主肢选用:18号角钢b×d×r=180×18×18mm；缀条选用:20号角钢b×d×r=180×24×18mm；主肢的截面力学参数为 A0=，Z0=，Ix0=，Iy0=；缀条的截面力学参数为 At=；格构柱截面示意图格构柱的y-y轴截面总惯性矩：格构柱的x-x轴截面总惯性矩：经过计算得到：Ix=4×[+×(65/2]=；Iy=4×[+×(65/2]= cm4；2. 格构柱的长细比计算：格构柱主肢的长细比计算公式：其中 H ──格构柱的总计算长度，取；I ──格构柱的截面惯性矩，取,Ix=，Iy=；A0 ──一个主肢的截面面积，取。

经过计算得到x=,y=。

3. 格构柱的整体稳定性计算：格构柱在弯矩作用平面内的整体稳定性计算公式：其中 N ──轴心压力的计算值(N)；取 N=4×105N；A──格构柱横截面的毛截面面积，取4×；──轴心受压构件弯矩作用平面内的稳定系数；根据换算长细比0x=,0y=≤150（容许长细比）满足要求!经过计算得到：X方向的强度值为mm2，不大于设计强度205N/mm2,所以满足要求! Y方向的强度值为mm2，不大于设计强度205N/mm2,所以满足要求!。

格构柱计算格构柱重量及总金额一、高度：-16.3至-2.4米，总高度：13.9米二、四肢杆：∠180×16单根截面积：（0.18×2-0.016）×0.016=0.005504m2 单根体积：0.005504×13.9=0.00.0765056m3 单根重量：0.0795056×7.85=0.6吨四根总重：0.6×4=2.4吨三、缀条：∠80×5@500单根截面积：（0.08×2-0.005）×0.005=0.000775m2 每米体积：0.000775×1=0.000775m3 每米重量：0.000775×7.85=0.00608吨单面长度：13.9m÷0.5×1=27.8m 四面总长度：27.8×4=111.2m四面总重量：0.00608×111.2=0.6765吨=0.676吨四、一道撑与立柱节点1、100×100×12三角钢板8块2、4Φ25U形筋3、700×700×12钢板3 体积：0.7×0.7×0.012=0.00588 m3重量：0.00588m×7.85=0.046158=0.046吨五、第二道撑与立柱节点1、200×200×14三角钢板8块M1=0.2×0.2×4=0.16 m22、950×200×14钢板2块M2=0.95×.02×2=0.38 m23、550×200×14钢板2块M3=0.55×0.2×2=0.22 m24、总体积：（M1+M2+M3）×0.014=0.01064m35、总重量：0.01064m3×7.85=0.083524=0.083吨六、第三道撑与立柱节点1、200×200×14三角钢板8块M1=0.2×0.2×4=0.16 m22、950×200×14钢板2块M2=0.95×.02×2=0.38 m23、550×200×14钢板2块M3=0.55×0.2×2=0.22 m24、总体积：（M1+M2+M3）×0.014=0.01064m35、总重量：0.01064m3×7.85=0.083524=0.083吨七、单根总重G=2.4+0.676+0.046+0.083+0.083=3.288吨八、总根数：157-2.5=154.5九、总重：3.288×154.5=507.99吨十、总金额：507.99×2550=1295389.8元感谢您的阅读，祝您生活愉快。

（1）截面形式轴心受格构柱一般采用双轴对称对称截面。

常用的截面形式是用两根槽钢或工字钢作为肢件（图a～c），有时也采用四个角钢或三个圆管作为肢件（图d、e）。

格构柱的优点是肢件间的距离可以调整，能使构件对两个主轴的稳定性相等。

工字钢作为肢件的截面一般用于受力较大的构件。

用四个角钢作肢件的截面形式往往用于受力较小而长细比较大的构件。

肢件采用槽钢时，宜采用图a的形式，在轮廓尺寸相同的情况下，可得到较大的惯性矩 Ix，比较经济而且外观平整，便于和其他构件连接。

缀条式格构柱常采用角钢作为缀条。

缀条可布置成不带横杆的三角形体系或带横杆的三角形体系。

缀板式格构柱常采用钢板作为缀板。

（2）截面的初步选择设计截面时，首先应根据使用要求、受力大小和材料供应情况等选择柱的形式。

中、小型柱可用缀条柱或缀板柱，大型柱宜采用缀条柱。

然后根据轴力 N 和两个主轴方向的计算长度（ l0x 和l0y）初步选定截面尺寸。

具体步骤如下：①计算对实轴的整体稳定，用与实腹柱相同的方法和步骤选出肢件的截面规格。

②计算对虚轴的整体稳定以确定两肢间的距离。

为了获得等稳定性，应使λx = λy（ x为虚轴，y 为实轴）。

用换算长细比的计算公式，即可解得格构柱的λx，对于双肢格构柱则有缀条柱缀板柱由λx 求出对虚轴所需的回转半径ix= l0x/λx，可得柱的h≈ ix/a1。

（1）强度验算强度验算公式与实腹柱相同。

柱的净截面面积 An不应计入缀条或缀板的截面面积。

（2）整体稳定验算分别对实轴和虚轴验算整体稳定性。

对实轴作整体稳定验算时与实腹柱相同。

对虚轴作整体稳定验算时，轴心受压构件稳定系数应按换算长细比λ0x查出。

换算长细比λ0x，则按相关知识表中的有关公式计算。

（3）单肢验算格构柱在两个缀条或缀板相邻节点之间的单肢是一个单独的轴心受压实腹构件。

它的长细比为λ1=l0l/il，其中 l01为计算长度，对缀条柱取缀条节点间的距离，对缀板柱焊接时取缀板间的净距离（图）；螺栓连接时，取相邻两缀板边缘螺栓的最近距离； i1为单肢的最小回转半径，即图中单肢绕1－1轴的回转半径。

架桥机拼装支架安全性计算一、拼装方案说明桥台与相邻桥墩间作为拼装场所，填土整平，封闭层采用 20cm 厚级配碎石。

支架基础为50cm厚C35 砼，平面尺寸为×6.34m （两个）。

支架采用钢轨压杆（由四根43kg/m 钢轨组成），数量为32 个，高度。

架桥机主梁拼装完成后整体吊装，其他结构件分别吊装。

二、钢轨柱极限承载力计算支架采用 43kg/m 钢轨组成的格构式钢轨柱，总高度为。

中间用缀板进行连接，缀板高度为。

两端为××0.03m 的钢板。

整个高度的尺寸为：。

钢轨柱断面尺寸以下所示：绕 x、y 轴的辗转半径为：I x’= √(I ’x；I y’= √(I ’y四肢格构式轴心受压构件当缀材为缀板时，《钢结构设计规范》规定换算长细比按下式计算：λox=√(λx2+λ1x 2);λoy=√(λx2+λ2y 2)λx、λ y—整个构件对x、y轴的长细比；λ1x、λ 1x —分肢长细比。

1、分肢长细比λ1x、λ1xλ 1x=L o1/i1x=L o1/i x’；λ 2y=L o2/i2y=L o2/i y =1340mm/21.357mm=62.743;’2、λx、λx辗转半径 I x、I yI22]= √[(c/2)2’2 x=√[(c/2)+i 1x+(i x ) ] =√[(458/2)22；I y=√[(c/2)22]= √[(c/2)2+(i’2] +i 2y y )=√[(486/2)22；(1)两端固准时λx x ×；（在 yoz 平面内两端固定）λy 2 ×6310mm/243.937mm =12.934;（在 xoz 平面内两端固定）(2)一端固定，一段自由λx=2L/i x=2×；（在 yoz 平面内两端固定）λy=2L/i 2=2×6310mm/243.937mm=51.735;（在 xoz 平面内两端固定）3、换算长细比λox、λoy(1)两端固定λo x=√(λx 2+λ1x 2)=√22)=29.465;λo y=√(λx 2+λ2y 2)=√22；(2)一端固定，一段自由λo x=√(λx 2+λ1x 2)=√22)=59.836;λo y=√(λx 2+λ2y 2)=√22；4、极限承载力N(1)两端固定λo x ，查表知牢固系数φ x=0.938;λo y ，查表知牢固系数φ x由(N+G自重 )/ φA≤[ σ] 知：φx时：N≤ 0.938 ×5700×215-(44.653 ×6.31 ×9.8 ×4)=1138.474 ×103N=1138.474KN;φx时：N≤ 0.785 ×5700×215-(44.653 ×6.31 ×9.8×× 103N=950.972KN;(2)一端固定，一段自由λo x=59.836;查表知牢固系数φ x=0.808;λo y ，查表知牢固系数φ x由(N+G自重 )/ φA≤[ σ] 知：φx时：N≤ 0.808 ×5700×215-(44.653 ×6.31 ×9.8 ×4)×103N=979.159KN;φx时：N≤ 0.679 ×5700×215-(44.653 ×6.31 ×9.8 ×4)× 103N=821.069KN;因此：1、两端若是在yoz 和 xoz 面内固结时，其最大承载力N=950.972KN;2、两端若是在yoz 和 xoz 面内一端固定、一端铰接时，其最大承载力。

§6-7格构式轴心受压构件6.7.1 格构式轴心受压构件绕实轴的整体稳定格构式受压构件也称为格构式柱(latticed columns，其分肢通常采用槽钢和工字钢，构件截面具有对称轴（图6.1.1）。

当构件轴心受压丧失整体稳定时，不大可能发生扭转屈曲和弯扭屈曲，往往发生绕截面主轴的弯曲屈曲。

因此计算格构式轴心受压构件的整体稳定时，只需计算绕截面实轴和虚轴抵抗弯曲屈曲的能力。

格构式轴心受压构件绕实轴的弯曲屈曲情况与实腹式轴心受压构件没有区别，因此其整体稳定计算也相同，可以采用式(6.4.2按b类截面进行计算。

6.7.2 格构式轴心受压构件绕虚轴的整体稳定1. 双肢格构式轴心受压构件实腹式轴心受压构件在弯曲屈曲时，剪切变形影响很小，对构件临界力的降低不到1%，可以忽略不计。

格构式轴心受压构件绕虚轴弯曲屈曲时，由于两个分肢不是实体相连，连接两分肢的缀件的抗剪刚度比实腹式构件的腹板弱，构件在微弯平衡状态下，除弯曲变形外，还需要考虑剪切变形的影响，因此稳定承载力有所降低。

根据弹性稳定理论分析，当缀件采用缀条时，两端铰接等截面格构式构件绕虚轴弯曲屈曲的临界应力为：构式轴心受压构件(图6.1.2d缀条的三肢组合构件(图6.1.2d6.7.3 格构式轴心受压构件分肢的稳定和强度计算格构式轴心受压构件的分肢既是组成整体截面的一部分，在缀件节点之间又是一个单独的实腹式受压构件。

所以，对格构式构件除需作为整体计算其强度、刚度和稳定外，还应计算各分肢的强度、刚度和稳定，且应保证各分肢失稳不先于格构式构件整体失稳。

一、分肢稳定和强度的计算方法1.分肢内力的确定构件总挠度曲线为2．分肢稳定的验算①对缀条式构件：图7.7.1格构式轴心受压构件弯曲屈曲稳定和强度求v0的简化计算方法(规范规定的方法①由钢构件制造容许最大初弯曲l/1000，考虑其它初始缺陷按经验近似地规定v0=l/500右l/400等。

②根据构件边缘纤维屈服准则来确定v0。

格构式轴心受压柱缀材的计算内力
格构式轴心受压柱缀材的计算内力包括以下步骤：
1.根据设计要求和建筑规范，确定缀材的材质、尺寸和承载能力。

2.根据缀材的实际长度和受力情况，确定其所受压力的大小。

3.根据公式计算缀材所受的压力，公式为：N =
(π^2*E*I)/(KL/r)^2，其中N为缀材受力大小，E为缀材的弹性模量，I为缀材的截面惯性矩，K为约束系数，L为缀材的长度，r为缀材的
半径或截面宽度。

4.判断计算得到的内力是否超过了缀材的承载能力，如果超过了，则需要重新设计或采用更为强度的材料。

一．荷载统计中柱承受的荷载面积为9×8=72 m2，已知楼板结构层折算厚度为200mm，双面抹灰总厚度为60mm，混凝土的容重为25KN/ m3，抹灰层按照水泥砂浆计算，容重为20KN/ m3，则可知：中柱主要承受的恒荷载为F G=72×0.2×25+72×0.06×20=446.4KN学号为12，12÷4=3，活荷载为3×1.5＋20=24.5KN/㎡中柱主要承受的活荷载为F Q=72×24.5=1764KN由《建筑结构荷载规范》中规定：对标准值大于4KN/m2的工业房屋楼面结构的活荷载应取1.3。

则有：N=γG F G×γQ F Q=1.2×446.4+1.3×1764=2828.88KN二、柱截面设计已知柱高为8m，截面类型为b类，所用钢品种为Q235-B，一端固接一端铰接，则可推断出计算长度l ox=l oy=0.8×8=6.4m。

A.初选分肢截面并验算柱绕实轴的刚度和整体稳定1.假定绕实轴的长细比λyˊ=60，由《钢结构设计原理》附表查得φ=0.807。

2.求A r、i y r所需截面面积A r=N/φf=2828.88×103/(0.807×215)=16304.314mm2所需回转半径i y r = l oy /λyˊ=6400/60=107mm3.查型钢表选择从钢结构设计原理附表中可以查，试选2根40a的工字型钢A=2×86.1=172.2cm2i y=15.9cm 。

其他截面特性i1=2.77cm I1=660cm4 Z0=142/2=714.验算绕实轴的刚度和整体稳定λy= l oy/ i y=6400/159=40.25 <[λ]=150 故绕实轴刚度满足根据Ｑ235 λy＝40.25 b类截面查得φy=0.898σ=N/φA=2828.88×103/（0.898×17220）=182.9N/mm2<f=215N/ mm2故绕实轴整体稳定满足。

格构柱缀板数量计算公式
假设需要构筑一座矩形的格构柱缀板，计算出所需的数量。

假设矩形的长为L，宽为W，柱缀板的宽度为B。

1.计算柱的数量：
柱的数量=(L/B+1)*(W/B+1)
其中，L/B和W/B分别表示长和宽的柱缀板数量，需要加1是因为需要考虑两侧的柱。

2.计算横向格构梁的数量：
横向格构梁的数量=(L/B)*(W/B+1)
其中，L/B表示长的柱缀板数量，W/B+1表示宽的柱缀板数量，需要加1是因为需要考虑一侧的柱。

3.计算纵向格构梁的数量：
纵向格构梁的数量=(L/B+1)*(W/B)
其中，L/B+1表示长的柱缀板数量，W/B表示宽的柱缀板数量，需要加1是因为需要考虑一侧的柱。

总的格构柱缀板数量=柱的数量+横向格构梁的数量+纵向格构梁的数量
需要注意的是，这里所计算的柱缀板数量是理论数量，并没有考虑到实际施工的浪费和材料的接长。

在实际施工中，需要根据具体情况进行一定的调整和浪费率的考虑。

格构式柱计算内容概括：
一、柱身计算
1、 强度： f A N
n ≤
2、 刚度：实轴：[]λλ≤y 、 虚轴：换算长细比[]λλ≤ox 缀板式：212λλλ+=x ox 缀条式：x x ox A A 1227+=
λλ 3、 整体稳定性：实轴：f A N y ≤ϕ 、虚轴：f A N
x ≤ϕ
4、 局部稳定：型钢所以满足
二、分肢稳定：保证分肢不先于柱身失稳，限制分肢长细比 缀条式：max 17.0λλ≤ ；缀板式：max 15.0λλ≤和40
{}y ox λλλ,max max =，且当为缀板式时还应不小于50。

三、缀材计算
1求V ： =V 23585y f Af
2、求缀材内力： 缀条：ααcos 2cos 1n V
n V N t == 缀板：剪力：a l V T 1=
弯矩：21l V M =
3、缀材验算： 缀条：按t N 作用下的轴心受压构件计算，并考虑强度折减系数η
1) 强度：f A N nL t
η≤
2) 刚度：[]λλ≤L max
3) 整体稳定：f A N L
t ηϕ≤min 4) 局部稳定： 型钢，∴ 安全。

缀板：强度：f W M
b ≤=σ， b A T 5.1=τ
刚度：缀板线刚度之和与分肢线刚度之比不小于6 611≥∑l I a I b
，：缀板中心距：分肢轴间距，1l a。

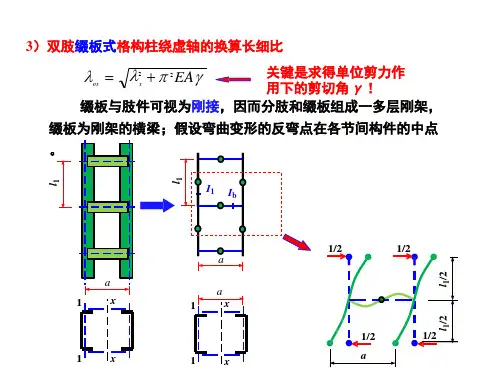
N=1.35γ0N k =数据001kN钢格构柱主肢角钢参数： L160×12单肢力学特性为：A 1=数据002mm 2， z 0=数据003mm, I x1=数据004mm 4。

缀板截面参数：厚度t b =数据005mm 2格构柱截面参数：柱截面宽a=数据006mm ，柱长l o =数据007mm两缀板间的净距离l=数据008mm（1） 格构柱整体稳定性验算组合构件对x 轴的惯性矩为：211042x x a I I A z ⎡⎤⎛⎫=⨯+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦=数据009mm 4回转半径：==x i 数据010mm 长细比：0x xL i λ==数据011 单肢长细比：11l i λ==数据012换算长细比：0x λ==数据013查表：ϕ=数据014稳定性验算：N Aϕ=数据015215MPa MP <，满足设计要求。

（2） 受压构件单肢自身的稳定性验算缀板中心距a=数据016mm单肢回转半径1i =数据017 单肢长细比1a iλ==数据018<max 0.5λ=25 （3） 缀板稳定性验算单肢轴线间净距c=数据019mm轴心受压构件的最大剪力：max V ==数据020N缀板的剪力：max 2a T V c==数据021 N 缀板的弯矩：max 4a M V ==数据022 N ·mm 缀板厚度：tb =数据023mm 缀板高度：h =数据024mm 缀板截面的截面模量：2212b t h W =⨯=数据025 mm 3 缀板强度验算：M Wσ==数据026 N/mm 2< 215N/mm 2，满足要求。

1.5b T ht τ==数据027 N/mm 2< 215N/mm 2，满足要求。

格构式轴心受压构件6.7.1 格构式轴心受压构件绕实轴的整体稳定格构式受压构件也称为格构式柱(latticed columns)，其分肢通常采用槽钢和工字钢，构件截面具有对称轴（图6.1.1）。

当构件轴心受压丧失整体稳定时，不大可能发生扭转屈曲和弯扭屈曲，往往发生绕截面主轴的弯曲屈曲。

因此计算格构式轴心受压构件的整体稳定时，只需计算绕截面实轴和虚轴抵抗弯曲屈曲的能力。

格构式轴心受压构件绕实轴的弯曲屈曲情况与实腹式轴心受压构件没有区别，因此其整体稳定计算也相同，可以采用式(6.4.2)按b类截面进行计算。

6.7.2 格构式轴心受压构件绕虚轴的整体稳定1.双肢格构式轴心受压构件实腹式轴心受压构件在弯曲屈曲时，剪切变形影响很小，对构件临界力的降低不到1%，可以忽略不计。

格构式轴心受压构件绕虚轴弯曲屈曲时，由于两个分肢不是实体相连，连接两分肢的缀件的抗剪刚度比实腹式构件的腹板弱，构件在微弯平衡状态下，除弯曲变形外，还需要考虑剪切变形的影响，因此稳定承载力有所降低。

根据弹性稳定理论分析，当缀件采用缀条时，两端铰接等截面格构式构件绕虚轴弯曲屈曲的临界应力为：构式轴心受压构件(图6.1.2d)缀条的三肢组合构件(图6.1.2d)6.7.3 格构式轴心受压构件分肢的稳定和强度计算格构式轴心受压构件的分肢既是组成整体截面的一部分，在缀件节点之间又是一个单独的实腹式受压构件。

所以，对格构式构件除需作为整体计算其强度、刚度和稳定外，还应计算各分肢的强度、刚度和稳定，且应保证各分肢失稳不先于格构式构件整体失稳。

一、分肢稳定和强度的计算方法分肢内力的确定构件总挠度曲线为2．分肢稳定的验算①对缀条式构件：图7.7.1格构式轴心受压构件弯曲屈曲稳定和强度求v0的简化计算方法(规范规定的方法)①由钢构件制造容许最大初弯曲l/1000，考虑其它初始缺陷按经验近似地规定v0=l/500右l/400等。

②根据构件边缘纤维屈服准则来确定v0。

格构式轴心受压构件6.7.1 格构式轴心受压构件绕实轴的整体稳定格构式受压构件也称为格构式柱(latticed columns)，其分肢通常采用槽钢和工字钢，构件截面具有对称轴（图6.1.1）。

当构件轴心受压丧失整体稳定时，不大可能发生扭转屈曲和弯扭屈曲，往往发生绕截面主轴的弯曲屈曲。

因此计算格构式轴心受压构件的整体稳定时，只需计算绕截面实轴和虚轴抵抗弯曲屈曲的能力。

格构式轴心受压构件绕实轴的弯曲屈曲情况与实腹式轴心受压构件没有区别，因此其整体稳定计算也相同，可以采用式(6.4.2)按b类截面进行计算。

6.7.2 格构式轴心受压构件绕虚轴的整体稳定1.双肢格构式轴心受压构件实腹式轴心受压构件在弯曲屈曲时，剪切变形影响很小，对构件临界力的降低不到1%，可以忽略不计。

格构式轴心受压构件绕虚轴弯曲屈曲时，由于两个分肢不是实体相连，连接两分肢的缀件的抗剪刚度比实腹式构件的腹板弱，构件在微弯平衡状态下，除弯曲变形外，还需要考虑剪切变形的影响，因此稳定承载力有所降低。

根据弹性稳定理论分析，当缀件采用缀条时，两端铰接等截面格构式构件绕虚轴弯曲屈曲的临界应力为：构式轴心受压构件(图6.1.2d)缀条的三肢组合构件(图6.1.2d)6.7.3 格构式轴心受压构件分肢的稳定和强度计算格构式轴心受压构件的分肢既是组成整体截面的一部分，在缀件节点之间又是一个单独的实腹式受压构件。

所以，对格构式构件除需作为整体计算其强度、刚度和稳定外，还应计算各分肢的强度、刚度和稳定，且应保证各分肢失稳不先于格构式构件整体失稳。

一、分肢稳定和强度的计算方法1.分肢内力的确定构件总挠度曲线为2．分肢稳定的验算①对缀条式构件：图7.7.1格构式轴心受压构件弯曲屈曲稳定和强度求v0的简化计算方法(规范规定的方法)①由钢构件制造容许最大初弯曲l/1000，考虑其它初始缺陷按经验近似地规定v0=l/500右l/400等。

②根据构件边缘纤维屈服准则来确定v0。