格构柱计算

钢结构连接、钢结构强度稳定性、钢筋支架、格构柱计算◆钢结构连接计算一、连接件类别不焊透的对接焊缝二、计算公式1．在通过焊缝形心的拉力，压力或剪力作用下的焊缝强度按下式计算：2．在其它力或各种综合力作用下，σf，τf共同作用处。

式中N──-构件轴心拉力或轴心压力，取 N＝100N；lw──对接焊缝或角焊缝的计算长度，取lw=50mm；γ─-作用力与焊缝方向的角度γ=45度；σf──按焊缝有效截面(helw)计算，垂直于焊缝长度方向的应力；hf──较小焊脚尺寸，取 hf=30mm；βt──正面角焊缝的强度设计值增大系数；取1；τf──按焊缝有效截面计算，沿焊缝长度方向的剪应力；Ffw──角焊缝的强度设计值。

α──斜角角焊缝两焊脚边的夹角或V形坡口角度；取α=100度。

s ──坡口根部至焊缝表面的最短距离，取 s=12mm；he──角焊缝的有效厚度，由于坡口类型为V形坡口，所以取he=s=12.000mm.三、计算结果1. 正应力：σf=N×sin(γ)/(lw×he)=100×sin(45)/(50×12.000)=0.118N/mm2；2. 剪应力：τf=N×cos(γ)/(lw×he)=100×cos(45)/(50×12.000)=0.118N/mm2；3. 综合应力：[(σf/βt)2+τf2]1/2=0.167N/mm2；结论:计算得出的综合应力0.167N/mm2≤对接焊缝的强度设计值ftw=10.000N/mm2，满足要求！◆钢结构强度稳定性计算一、构件受力类别：轴心受弯构件。

二、强度验算：1、受弯的实腹构件，其抗弯强度可按下式计算：Mx/γxWnx + My/γyWny ≤ f式中 Mx，My──绕x轴和y轴的弯矩，分别取100.800×106 N·mm,10.000×106 N·mm；γx, γy──对x轴和y轴的截面塑性发展系数，分别取 1.2,1.3；Wnx,Wny──对x轴和y轴的净截面抵抗矩,分别取 947000 mm3,85900 mm3；计算得：Mx/(γxWnx)+My/(γyWny)=100.800×106/(1.2×947000)+10.000×106/(1.3×85900)=178.251 N/mm2受弯的实腹构件抗弯强度=178.251 N/mm2 ≤抗弯强度设计值f=215N/mm2，满足要求！2、受弯的实腹构件，其抗剪强度可按下式计算：τmax = VS/Itw ≤ fv式中V──计算截面沿腹板平面作用的剪力,取V=10.300×103 N；S──计算剪力处以上毛截面对中和轴的面积矩,取 S= 947000mm3；I──毛截面惯性矩,取 I=189300000 mm4；tw──腹板厚度,取 tw=8 mm；计算得：τmax = VS/Itw=10.300×103×947000/(189300000×8)=6.441N/mm2受弯的实腹构件抗剪强度τmax =6.441N/mm2≤抗剪强度设计值fv = 175 N/mm2，满足要求！3、局部承压强度计算τc = φF/twlz ≤ f式中φ──集中荷载增大系数，取φ=3；F──集中荷载,对动力荷载应考虑的动力系数，取 F=0kN；tw──腹板厚度,取 tw=8 mm；lz──集中荷载在腹板计算高度上边缘的假定分布长度，取lz=100(mm)；计算得：τc = φF/twlz =3×0×103/(8×100)=0.000N/mm2局部承压强度τc =0.000N/mm2≤承载力设计值f = 215 N/mm2，满足要求！4、在最大刚度主平面内受弯的构件，其整体稳定性按下式计算：Mx/φbWx ≤ f式中Mx──绕x轴的弯矩，取100.8×106 N·mm；φb──受弯构件的整体稳定性系数,取φb= 0.9；Wx──对x轴的毛截面抵抗矩Wx,取 947000 mm3；计算得：Mx/φbwx = 100.8×106/(0.9×947000)=118.268 N/mm2≤抗弯强度设计值f= 215 N/mm2，满足要求！5、在两个主平面受弯的工字形截面构件，其整体稳定性按下式计算：Mx/φbWx + My/γyWny ≤ f式中 Mx，My──绕x轴和y轴的弯矩，分别取100.8×106 N·mm,10×106 N·mm；φb──受弯构件的整体稳定性系数,取φb= 0.9；γy──对y轴的截面塑性发展系数，取 1.3；Wx,Wy──对x轴和y轴的毛截面抵抗矩,分别取 947000 mm3, 85900 mm3；Wny──对y轴的净截面抵抗矩,取 85900 mm3计算得：Mx/φbwx +My/ γyWny =100.8×106/(0.9×947000)+10×106/(1.3×85900)=207.818 N/mm2≤抗弯强度设计值f=215 N/mm2，满足要求！◆钢筋支架计算公式一、参数信息钢筋支架（马凳）应用于高层建筑中的大体积混凝土基础底板或者一些大型设备基础和高厚混凝土板等的上下层钢筋之间。

塔吊桩基础的计算书一. 参数信息塔吊型号: QTZ63 自重(包括压重):F1=450.80kN 最大起重荷载: F2=60.00kN塔吊倾覆力距: M=630.00kN.m 塔吊起重高度: H=101.00m 塔身宽度: B=1.80m桩混凝土等级: C35 承台混凝土等级:C35 保护层厚度: 50mm矩形承台边长: 4.00m 承台厚度: Hc=1.35m 承台箍筋间距: S=200mm承台钢筋级别: Ⅱ级承台预埋件埋深:h=0.5m 承台顶面埋深: D=0.00m桩直径: d=0.80m 桩间距: a=2.00m 桩钢筋级别: Ⅱ级桩入土深度: 34.00 桩型与工艺: 泥浆护壁钻(冲)孔灌注桩二. 塔吊基础承台顶面的竖向力与弯矩计算1. 塔吊自重(包括压重)F1=450.80kN2. 塔吊最大起重荷载F2=60.00kN作用于桩基承台顶面的竖向力 F=F1+F2=510.80kN塔吊的倾覆力矩 M=1.4×630.00=882.00kN.m三. 矩形承台弯矩的计算计算简图：图中x轴的方向是随机变化的，设计计算时应按照倾覆力矩M最不利方向进行验算。

1. 桩顶竖向力的计算(依据《建筑桩基础技术规范》JGJ94-94的第5.1.1条)其中 n──单桩个数，n=4；F──作用于桩基承台顶面的竖向力设计值，F=510.80kN；G──桩基承台的自重，G=25.0×Bc×Bc×Hc+20.0×Bc×Bc×D=540.00kN；M x,M y──承台底面的弯矩设计值(kN.m)；x i,y i──单桩相对承台中心轴的XY方向距离(m)；N i──单桩桩顶竖向力设计值(kN)。

经计算得到单桩桩顶竖向力设计值:最大压力：N=1.2×(510.80+540.00)/4+882.00×(2.00×1.414/2)/[2×(2.00×1.414/2)2]=627.12kN最大拔力：N=(510.80+540.00)/4-882.00×(2.00×1.414/2)/[2×(2.00×1.414/2)2]=-49.18kN2. 矩形承台弯矩的计算(依据《建筑桩基础技术规范》JGJ94-94的第5.6.1条)其中 M x1,M y1──计算截面处XY方向的弯矩设计值(kN.m)；x i,y i──单桩相对承台中心轴的XY方向距离(m)；N i1──扣除承台自重的单桩桩顶竖向力设计值(kN)，N i1=N i-G/n。

§6—7格构式轴心受压构件6.7。

1 格构式轴心受压构件绕实轴的整体稳定格构式受压构件也称为格构式柱（latticed columns，其分肢通常采用槽钢和工字钢，构件截面具有对称轴（图6。

1.1）。

当构件轴心受压丧失整体稳定时，不大可能发生扭转屈曲和弯扭屈曲，往往发生绕截面主轴的弯曲屈曲。

因此计算格构式轴心受压构件的整体稳定时,只需计算绕截面实轴和虚轴抵抗弯曲屈曲的能力。

格构式轴心受压构件绕实轴的弯曲屈曲情况与实腹式轴心受压构件没有区别,因此其整体稳定计算也相同,可以采用式(6。

4.2按b类截面进行计算。

6。

7。

2 格构式轴心受压构件绕虚轴的整体稳定1。

双肢格构式轴心受压构件实腹式轴心受压构件在弯曲屈曲时,剪切变形影响很小，对构件临界力的降低不到1%，可以忽略不计。

格构式轴心受压构件绕虚轴弯曲屈曲时，由于两个分肢不是实体相连，连接两分肢的缀件的抗剪刚度比实腹式构件的腹板弱,构件在微弯平衡状态下,除弯曲变形外，还需要考虑剪切变形的影响，因此稳定承载力有所降低。

根据弹性稳定理论分析,当缀件采用缀条时，两端铰接等截面格构式构件绕虚轴弯曲屈曲的临界应力为：构式轴心受压构件(图6。

1。

2d缀条的三肢组合构件(图6.1。

2d6.7.3 格构式轴心受压构件分肢的稳定和强度计算格构式轴心受压构件的分肢既是组成整体截面的一部分,在缀件节点之间又是一个单独的实腹式受压构件。

所以，对格构式构件除需作为整体计算其强度、刚度和稳定外，还应计算各分肢的强度、刚度和稳定，且应保证各分肢失稳不先于格构式构件整体失稳。

一、分肢稳定和强度的计算方法1.分肢内力的确定构件总挠度曲线为2．分肢稳定的验算①对缀条式构件:图7。

7.1格构式轴心受压构件弯曲屈曲稳定和强度求v0的简化计算方法(规范规定的方法①由钢构件制造容许最大初弯曲l/1000,考虑其它初始缺陷按经验近似地规定v0=l/500右l/400等.②根据构件边缘纤维屈服准则来确定v0。

格构柱计算塔吊桩基础的计算书⼀. 参数信息塔吊型号: QTZ63 ⾃重(包括压重):F1=450.80kN 最⼤起重荷载: F2=60.00kN塔吊倾覆⼒距: M=630.00kN.m 塔吊起重⾼度: H=101.00m 塔⾝宽度: B=1.80m桩混凝⼟等级: C35 承台混凝⼟等级:C35 保护层厚度: 50mm矩形承台边长: 4.00m 承台厚度: Hc=1.35m 承台箍筋间距: S=200mm承台钢筋级别: Ⅱ级承台预埋件埋深:h=0.5m 承台顶⾯埋深: D=0.00m桩直径: d=0.80m 桩间距: a=2.00m 桩钢筋级别: Ⅱ级桩⼊⼟深度: 34.00 桩型与⼯艺: 泥浆护壁钻(冲)孔灌注桩⼆. 塔吊基础承台顶⾯的竖向⼒与弯矩计算1. 塔吊⾃重(包括压重)F1=450.80kN2. 塔吊最⼤起重荷载F2=60.00kN作⽤于桩基承台顶⾯的竖向⼒ F=F1+F2=510.80kN塔吊的倾覆⼒矩 M=1.4×630.00=882.00kN.m三. 矩形承台弯矩的计算计算简图：图中x轴的⽅向是随机变化的，设计计算时应按照倾覆⼒矩M最不利⽅向进⾏验算。

1. 桩顶竖向⼒的计算(依据《建筑桩基础技术规范》JGJ94-94的第5.1.1条)其中 n──单桩个数，n=4；F──作⽤于桩基承台顶⾯的竖向⼒设计值，F=510.80kN；G──桩基承台的⾃重，G=25.0×Bc×Bc×Hc+20.0×Bc×Bc×D=540.00kN；M x,M y──承台底⾯的弯矩设计值(kN.m)；x i,y i──单桩相对承台中⼼轴的XY⽅向距离(m)；N i──单桩桩顶竖向⼒设计值(kN)。

经计算得到单桩桩顶竖向⼒设计值:最⼤压⼒：N=1.2×(510.80+540.00)/4+882.00×(2.00×1.414/2)/[2×(2.00×1.414/2)2]=627.12kN最⼤拔⼒：N=(510.80+540.00)/4-882.00×(2.00×1.414/2)/[2×(2.00×1.414/2)2]=-49.18kN2. 矩形承台弯矩的计算(依据《建筑桩基础技术规范》JGJ94-94的第5.6.1条)其中 M x1,M y1──计算截⾯处XY⽅向的弯矩设计值(kN.m)；x i,y i──单桩相对承台中⼼轴的XY⽅向距离(m)；N i1──扣除承台⾃重的单桩桩顶竖向⼒设计值(kN)，N i1=N i-G/n。

§6-7格构式轴心受压构件6.7.1 格构式轴心受压构件绕实轴的整体稳定格构式受压构件也称为格构式柱(latticed columns，其分肢通常采用槽钢和工字钢，构件截面具有对称轴（图6.1.1）。

当构件轴心受压丧失整体稳定时，不大可能发生扭转屈曲和弯扭屈曲，往往发生绕截面主轴的弯曲屈曲。

因此计算格构式轴心受压构件的整体稳定时，只需计算绕截面实轴和虚轴抵抗弯曲屈曲的能力。

格构式轴心受压构件绕实轴的弯曲屈曲情况与实腹式轴心受压构件没有区别，因此其整体稳定计算也相同，可以采用式(6.4.2按b类截面进行计算。

6.7.2 格构式轴心受压构件绕虚轴的整体稳定1. 双肢格构式轴心受压构件实腹式轴心受压构件在弯曲屈曲时，剪切变形影响很小，对构件临界力的降低不到1%，可以忽略不计。

格构式轴心受压构件绕虚轴弯曲屈曲时，由于两个分肢不是实体相连，连接两分肢的缀件的抗剪刚度比实腹式构件的腹板弱，构件在微弯平衡状态下，除弯曲变形外，还需要考虑剪切变形的影响，因此稳定承载力有所降低。

根据弹性稳定理论分析，当缀件采用缀条时，两端铰接等截面格构式构件绕虚轴弯曲屈曲的临界应力为：构式轴心受压构件(图6.1.2d缀条的三肢组合构件(图6.1.2d6.7.3 格构式轴心受压构件分肢的稳定和强度计算格构式轴心受压构件的分肢既是组成整体截面的一部分，在缀件节点之间又是一个单独的实腹式受压构件。

所以，对格构式构件除需作为整体计算其强度、刚度和稳定外，还应计算各分肢的强度、刚度和稳定，且应保证各分肢失稳不先于格构式构件整体失稳。

一、分肢稳定和强度的计算方法1.分肢内力的确定构件总挠度曲线为2．分肢稳定的验算①对缀条式构件：图7.7.1格构式轴心受压构件弯曲屈曲稳定和强度求v0的简化计算方法(规范规定的方法①由钢构件制造容许最大初弯曲l/1000，考虑其它初始缺陷按经验近似地规定v0=l/500右l/400等。

②根据构件边缘纤维屈服准则来确定v0。

格构柱受力计算书
计算依据：
(1)《钢结构设计规范》(GB50017-2003)。

(2)《钢结构设计与计算》
1. 格构柱截面的力学特性：
格构柱的截面尺寸为×；
主肢选用:18号角钢b×d×r=180×18×18mm；
缀条选用:20号角钢b×d×r=180×24×18mm；
主肢的截面力学参数为A0=，Z0=，
Ix0=，Iy0=；
缀条的截面力学参数为At=；
格构柱截面示意图
格构柱的y-y轴截面总惯性矩：
格构柱的x-x轴截面总惯性矩：
经过计算得到：
Ix=4×[+×(65/2]=；
Iy=4×[+×(65/2]= cm4；
2. 格构柱的长细比计算：
格构柱主肢的长细比计算公式：
其中H ──格构柱的总计算长度，取；
I ──格构柱的截面惯性矩，取,Ix=，Iy=；
A0 ──一个主肢的截面面积，取。

经过计算得到x=,y=。

3. 格构柱的整体稳定性计算：
格构柱在弯矩作用平面内的整体稳定性计算公式：
其中N ──轴心压力的计算值(N)；取N=4×105N；
A──格构柱横截面的毛截面面积，取4×；
──轴心受压构件弯矩作用平面内的稳定系数；
根据换算长细比0x=,0y=≤150（容许长细比）满足要求!
经过计算得到：
X方向的强度值为mm2，不大于设计强度205N/mm2,所以满足要求!
Y方向的强度值为mm2，不大于设计强度205N/mm2,所以满足要求!。

角钢格构柱比重计算【实用版】目录1.角钢格构柱的概述2.角钢格构柱比重计算的必要性3.角钢格构柱比重的计算方法4.角钢格构柱比重计算的实际应用5.角钢格构柱比重计算的注意事项正文一、角钢格构柱的概述角钢格构柱是一种以角钢为构件的格构柱，主要应用于建筑结构、桥梁结构等领域。

角钢格构柱因其结构稳定性好、承载能力强、制作安装简便等优点而广泛应用。

二、角钢格构柱比重计算的必要性角钢格构柱在设计与计算过程中，需要对其材料性能、截面尺寸等进行分析，以确保其满足工程结构的稳定性和承载力要求。

其中，比重计算是重要的一环，可以确保材料的合理选型和使用。

三、角钢格构柱比重的计算方法角钢格构柱的比重计算主要包括以下步骤：1.确定角钢的材质和规格。

2.计算角钢的理论重量。

理论重量的计算公式为：W=0.00785×（b×h）×t，其中，b 为角钢的宽度，h 为角钢的高度，t 为角钢的厚度。

3.根据角钢的实际重量和理论重量，计算角钢的比重。

比重的计算公式为：ρ=实际重量/理论重量。

四、角钢格构柱比重计算的实际应用在实际工程中，角钢格构柱比重计算可以为设计人员提供重要依据，帮助他们选择合适的材料，以确保结构的稳定性和承载力。

同时，比重计算还可以为采购、成本控制等环节提供参考。

五、角钢格构柱比重计算的注意事项进行角钢格构柱比重计算时，应注意以下几点：1.选用正确的材质和规格。

2.确保计算过程中的数据准确。

3.注意单位换算，统一计算单位。

总之，角钢格构柱比重计算是保证工程结构稳定性和承载力的重要环节。

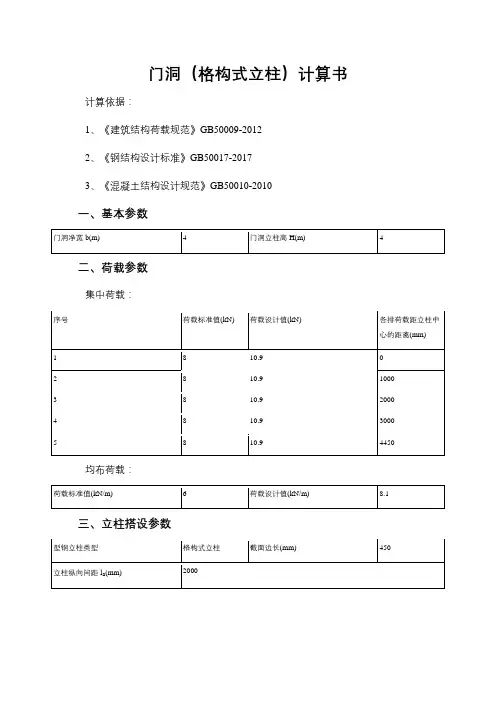
门洞（格构式立柱）计算书计算依据：1、《建筑结构荷载规范》GB50009-20122、《钢结构设计标准》GB50017-20173、《混凝土结构设计规范》GB50010-2010一、基本参数二、荷载参数集中荷载：均布荷载：三、立柱搭设参数正立面图侧立面图格构柱截面四、横梁计算均布荷载标准值q’=0.577+0.6×6=4.177kN/m均布荷载设计值q=1.2×0.577+0.6×8.1=5.552kN/m由于横梁2根合并，单根横梁承受集中荷载为p n=0.6×Fn 计算简图如下：1、抗弯验算横梁弯矩图(kN·m)σ=M max/W=28.668×106/726330=39.47N/mm2≤[f]=205N/mm2满足要求！2、挠度验算横梁变形图(mm)νmax＝1.794mm≤[ν]=1/250=4450/250=17.8mm满足要求！3、抗剪验算横梁剪力图(kN)V max＝23.157kNτmax=V max/(8I zδ)[bh02-(b-δ)h2]=23.157×1000×[132×3202-(132-11.5)×2902]/(8×116214000×11.5)＝7.327N/mm2≤[τ]=125N/mm2满足要求！4、支座反力计算承载能力极限状态R1＝29.697kN，R2＝27.709kN正常使用极限状态R'1＝22.023kN，R'2＝20.564kN五、立柱验算立柱所受横梁传递荷载N=max(R1,R2)/k1=max(29.697,27.709)/0.6=49.496kN 立柱所受轴力F=N+1.2×G k×H=49.496+1.2×1×4=54.296kN1、杆件轴心受拉强度验算分肢毛截面积之和：A=4A0=4×24.37×100=9748mm2σ=N/A=49.496×103/9748=5.078N/mm2≤[f]=205N/mm2满足要求！2、格构式钢柱换算长细比验算整个格构柱截面对X、Y轴惯性矩：I x=4[I0+A0(a/2-Z0)2]=4×[362+24.37×(45/2-3.45)2]=36823.736cm4整个构件长细比：λx=λy=L0/(I x/(4A0))0.5=400/(36823.736/(4×24.37))0.5=20.58分肢长细比：λ1=l01/i y0=31/2.48=12.5分肢毛截面积之和：A=4A0=4×24.37×100=9748mm2格构式钢柱绕两主轴的换算长细比：λ0max=(λx2+λ12)0.5=(20.582+12.52)0.5=24.079各格构柱轴心受压稳定系数：λ01max=24.079≤[λ]=150，查规范表得：φ1=0.956满足要求！σ1＝F/(φ1A)=54295.572/(0.956×9748)=5.826N/mm2≤[f]=205N/mm2满足要求！3、格构式钢柱分肢的长细比验算λ1=12.5≤min(0.5λ01max,40)=min(0.5×50,40)=25根据GB50017-2017，7.2.5条，当λmax<50时，取50满足要求！六、立柱基础验算立柱传给基础荷载F=54.296kN混凝土基础抗压强度验算σ=F/A=54.296×103/(1×106)=0.054N/mm2≤f c=16.7N/mm2满足要求！立柱底面平均压力p＝F/(m f A)＝54.296/(0.5×1)＝108.591kPa≤f ak＝300kPa 满足要求！。

塔吊基础计算（格构柱）塔吊基础计算（格构柱）八、基础验算基础承受的垂直力：P=449KN 基础承受的水平力:（一）、塔吊桩竖向承载力计算:单桩桩顶竖向力计算 单桩竖向力设计值按下式计算:Qik=（ P + G ）/n ± M/a 血式中：Q 汰一ffl 应于荷载效应标准组合偏心竖向力作用下第i 根 桩的竖向力；P —塔吊桩基础承受的垂直力,P=449KN ; G = (4.8 x 4.8 x 0.4+4-8 x 4.8 x 1.3} x25 = 979.2KN;P + G=449 + 979.2 = 1428.2 KN n —tS 根数,n=4 ; M —桩基础承受的倾翻力矩f M = 1668+71 x1.3 = 1760.3KN.m;a —1 庄中心距,a = 3.2m o Q ik =142&2/4±1760・3/3・2x 逅H=71KN基础承受的倾翻力矩:M = 1668KN.mG —桩承台单桩最大压力:Q 压=357.05 + 389.03 = 746.08KN 单桩最大拔力:Q 拔=357.05-389.03 = -31.98KN2. 桩承载力计算:(1) .单桩竖向承载力特征值按下式计算:Ra = qpaAp+UpJqsiaLiq P a. qsiU 端阻力,桩侧阻力特征值； Ap_脈端横截面面积； uurn 周边长度； Li —第i 层岩土层的厚度。

5号塔吊桩:对应的是8-8剖的Z52。

桩顶标高为-6.8m ,绝对标高为,取有效桩长,桩端进入粘土层。

式中：Ra —单桩竖向承载力特征值；3. 承台基础的验算(1 )承台弯矩计算叫1 =工％X性1 =工Ml 吗Mxl = Myl=2 x (746.08-979.2/4) x(3.2/1.414) = 2268.88KN*m(2) 承台截面受力主筋4 KMA = -------0必昉配筋面积 As = 1.4 X 2268.88 x 106/(0.9 x 1300 x 310) =8757<7mm 2塔吊承台配筋采用心22@180双层双向计27根r Ag =10258.38mm 2>As(3) 承台截面抗剪切验算Fo" < 亦&。

格构柱稳定性的计算计算依据：(1)《钢结构设计规范》(GB50017-2003)。

(2)《钢结构设计与计算》1. 格构柱截面的力学特性：格构柱的截面尺寸为0.65×0.65m；主肢选用:18号角钢b×d×r=180×18×18mm；缀条选用:20号角钢b×d×r=180×24×18mm；主肢的截面力学参数为 A0=61.95cm2，Z0=5.13cm，I x0=1881.12cm4，I y0=3338.25cm4；缀条的截面力学参数为 A t=61.95cm2；格构柱截面示意图格构柱的y-y轴截面总惯性矩：格构柱的x-x轴截面总惯性矩：经过计算得到：I x=4×[1881.12+61.95×(65/2-5.13)2]=193155.64cm4；I y=4×[1881.12+61.95×(65/2-5.13)2]=193155.64 cm4；2. 格构柱的长细比计算：格构柱主肢的长细比计算公式：其中 H ──格构柱的总计算长度，取18.40m；I ──格构柱的截面惯性矩，取,I x=193155.64cm4，I y=193155.64cm4； A0──一个主肢的截面面积，取61.95cm2。

经过计算得到x=65.90,y=65.90。

3. 格构柱的整体稳定性计算：格构柱在弯矩作用平面内的整体稳定性计算公式：其中 N ──轴心压力的计算值(N)；取 N=4×105N；A──格构柱横截面的毛截面面积，取4×61.95cm2；──轴心受压构件弯矩作用平面内的稳定系数；根据换算长细比0x=65.9,0y=65.90≤150（容许长细比）满足要求!经过计算得到：X方向的强度值为20.85N/mm2，不大于设计强度205N/mm2,所以满足要求!Y方向的强度值为20.85N/mm2，不大于设计强度205N/mm2,所以满足要求!。

角钢格构柱比重计算摘要：1.角钢格构柱的概述2.角钢格构柱比重计算的必要性3.角钢格构柱比重计算的方法4.角钢格构柱比重计算的实际应用5.角钢格构柱比重计算的注意事项正文：一、角钢格构柱的概述角钢格构柱是一种由角钢和钢板组成的钢结构柱，因其具有结构稳定、承载力强、制作简便等优点，被广泛应用于桥梁、输电塔、高层建筑等领域。

在工程设计中，为了保证角钢格构柱的稳定性和安全性，需要对其进行比重计算。

二、角钢格构柱比重计算的必要性比重计算是衡量角钢格构柱承载能力的重要手段，通过对角钢格构柱的比重进行精确计算，可以确保其在使用过程中不会因超载而发生变形或破坏，从而保证工程的安全性。

此外，比重计算还有助于优化角钢格构柱的设计和选材，提高其经济性和实用性。

三、角钢格构柱比重计算的方法角钢格构柱的比重计算主要包括以下步骤：1.确定角钢格构柱的材料和尺寸。

在计算比重之前，需要先明确角钢格构柱所使用的材料（如角钢、钢板等）及其尺寸。

2.计算角钢格构柱的截面面积。

根据角钢格构柱的材料和尺寸，可以计算出其截面面积。

3.计算角钢格构柱的重量。

根据角钢格构柱的截面面积和材料密度，可以计算出角钢格构柱的重量。

4.计算角钢格构柱的比重。

将角钢格构柱的重量除以其截面面积，即可得到角钢格构柱的比重。

四、角钢格构柱比重计算的实际应用在实际工程中，角钢格构柱的比重计算可以帮助工程师准确评估其承载能力，从而确保工程的安全性。

例如，在桥梁工程中，通过比重计算可以确保角钢格构柱能够承受车辆和行人的重量，以及风、雪等自然因素对桥梁的影响。

五、角钢格构柱比重计算的注意事项在进行角钢格构柱比重计算时，应注意以下几点：1.确保计算过程中的数据准确无误，以免影响最终结果的准确性。

2.在选取材料时，应根据实际工程需求选择合适的材料，并在计算中予以明确。

3.在计算过程中，应充分考虑工程实际中可能遇到的各种因素，如温度变化、材料老化等，以提高计算结果的可靠性。

格构柱的立柱计算方式
格构柱的立柱计算方式一般需要考虑以下几个因素：
1.受力情况：格构柱在承受垂直载荷和横向载荷时，需要根据具体情况确定应力状态和受力方向来计算立柱的截面尺寸和材料强度等。

2.梁柱比：格构柱的梁柱比对立柱尺寸的大小有着很大的影响，通常情况下，梁柱比越小，立柱尺寸就越小。

3.敲定截面形状：确定立柱的截面形状也是计算立柱尺寸的重要因素之一。

一般情况下，圆形截面比较常用。

4.材料强度：格构柱的立柱需要选用强度高、刚性好的材料，如钢和混凝土等。

5.安全系数：在计算格构柱的立柱时，需要考虑安全系数的影响。

常用的安全系数一般为2-3。

综上所述，格构柱的立柱计算需要考虑多个因素，必须按照实际情况进行综合考虑，才能得出合理的结果。

基坑支护中格构柱计算分析摘要：以实际基坑工程项目为例，分析基坑支护中格构柱的相关规范规定及计算方法，通过工程实例对格构柱的内力进行分步验算，方便设计人员在基坑支护设计中参考，有利于基坑支护工程设计及计算的标准化建设。

关键词：基坑支护；钢支撑；格构柱；计算算例为满足日益增长的市民出行，城市轨道交通的建设稳中有进。

地铁车站一般位于城市繁华地带，由于基坑周边建构筑物及交通等因素的限制，地铁车站的长条型基坑通常采用控制基坑变形较好且有利于重复使用的排桩+钢管内支撑结构进行支护，基坑宽度大于20m时，一般需要在基坑中间设置格构柱。

本文梳理了格构柱的相关规范规定，并通过计算实例进行格构柱的分析验算，便于设计人员参考使用。

我国现行《建筑基坑支护设计规程》JGJ 120-2012(以下简称“《支护规程》”)第4.9.10条第2款规定了单层支撑的立柱及多层支撑底层立柱的受压计算长度应取底层支撑底面至基坑底面的净高度与立柱直径或边长的5倍之和。

《支护规程》第4.9.15条规定了立柱长细比不宜大于25。

对于立柱计算，《支护规程》4.9.5条及4.9.10条规定，对于在内支撑结构上的竖向荷载较小，且内支撑结构的水平构件按连续梁计算时，立柱可按偏心受压构件计算。

对于钢支撑其竖向荷载较小，为简化计算，立柱按轴心受压构件考虑，但根据《支护规程》无法确定立柱的竖向轴力设计值，笔者查阅了相关规范，《广州地区建筑基坑支护技术规定》GJB 02-98(以下简称“《广州规定》”)第6.9.12条规定，立柱内力宜根据支撑条件按空间杆系结构力学计算，也可按轴心受压构件计算，轴线力设计值宜可按下式确定：其中结合以上规定，则可在围护计算查出支撑轴力标准值的情况下，较为简洁的进行立柱强度及稳定性验算。

结合以上分析，下面给出一个钢结构格构柱立柱的计算实例，方便设计人员参考使用。

某基坑支护形式为两道支撑结构，底层支撑中心距离基底竖向高度5m，立柱采用460×460mm角钢缀板式格构柱，角钢采用等边160×14mm，缀板采用420×300×10mm，相邻缀板中心距为0.7m，钢材牌号均为Q235，第一道支撑轴力标准值为1255kN，第二道支撑轴力标准值为7945kN，上部支撑、连系梁及施工荷载自重为80kN，则支撑传到立柱上的竖向力标准值为80+0.1（1255+7945）=1000kN，基坑安全等级为一级，重要性系数，根据以上条件验算立柱稳定性。

格构柱稳定性的计算依据《钢结构设计规范》(GB50017-2003)。

1.格构柱截面的力学特性：格构柱的截面尺寸为0.45×0.45m；主肢选用:20号角钢b×d×r=200×24×18mm；缀条选用:20号角钢b×d×r=200×24×18mm；主肢的截面力学参数为A0=90.66cm2，Z0=5.87cm，I x0=3338.25cm4，I y0=3338.25cm4；缀条的截面力学参数为A t=90.66cm2；格构柱截面示意图格构柱的y-y轴截面总惯性矩：格构柱的x-x轴截面总惯性矩：经过计算得到：I x=4×[3338.25+90.66×(45/2-5.87)2]=113644.70cm4；I y=4×[3338.25+90.66×(45/2-5.87)2]=113644.70cm4；2.格构柱的长细比计算：格构柱主肢的长细比计算公式：其中H──格构柱的总计算长度，取21.80m；I──格构柱的截面惯性矩，取,I x=113644.70cm4，I y=113644.70cm4；A0──一个主肢的截面面积，取90.66cm2。

经过计算得到x=123.15,y=123.15。

换算长细比计算公式：其中A──格构柱横截面的毛截面面积，取4×90.66cm2；A1──格构柱横截面所截垂直于x-x轴或y-y轴的毛截面面积，取2×90.66cm2；经过计算得到kx=123.47,ky=123.47。

3.格构柱的整体稳定性计算：格构柱在弯矩作用平面内的整体稳定性计算公式：其中N──轴心压力的计算值(kN)；取N=1130.42kN；A──格构柱横截面的毛截面面积，取4×90.66cm2；──轴心受压构件弯矩作用平面内的稳定系数；根据换算长细比0x=123.47,0y=123.47≤150满足要求!查《钢结构设计规范》得到x=0.42,y=0.42。

格构式轴心受压构件6.7.1 格构式轴心受压构件绕实轴的整体稳定格构式受压构件也称为格构式柱(latticed columns)，其分肢通常采用槽钢和工字钢，构件截面具有对称轴（图6.1.1）。

当构件轴心受压丧失整体稳定时，不大可能发生扭转屈曲和弯扭屈曲，往往发生绕截面主轴的弯曲屈曲。

因此计算格构式轴心受压构件的整体稳定时，只需计算绕截面实轴和虚轴抵抗弯曲屈曲的能力。

格构式轴心受压构件绕实轴的弯曲屈曲情况与实腹式轴心受压构件没有区别，因此其整体稳定计算也相同，可以采用式(6.4.2)按b类截面进行计算。

6.7.2 格构式轴心受压构件绕虚轴的整体稳定1.双肢格构式轴心受压构件实腹式轴心受压构件在弯曲屈曲时，剪切变形影响很小，对构件临界力的降低不到1%，可以忽略不计。

格构式轴心受压构件绕虚轴弯曲屈曲时，由于两个分肢不是实体相连，连接两分肢的缀件的抗剪刚度比实腹式构件的腹板弱，构件在微弯平衡状态下，除弯曲变形外，还需要考虑剪切变形的影响，因此稳定承载力有所降低。

根据弹性稳定理论分析，当缀件采用缀条时，两端铰接等截面格构式构件绕虚轴弯曲屈曲的临界应力为：构式轴心受压构件(图6.1.2d)缀条的三肢组合构件(图6.1.2d)6.7.3 格构式轴心受压构件分肢的稳定和强度计算格构式轴心受压构件的分肢既是组成整体截面的一部分，在缀件节点之间又是一个单独的实腹式受压构件。

所以，对格构式构件除需作为整体计算其强度、刚度和稳定外，还应计算各分肢的强度、刚度和稳定，且应保证各分肢失稳不先于格构式构件整体失稳。

一、分肢稳定和强度的计算方法1.分肢内力的确定构件总挠度曲线为2．分肢稳定的验算①对缀条式构件：图7.7.1格构式轴心受压构件弯曲屈曲稳定和强度求v0的简化计算方法(规范规定的方法)①由钢构件制造容许最大初弯曲l/1000，考虑其它初始缺陷按经验近似地规定v0=l/500右l/400等。

②根据构件边缘纤维屈服准则来确定v0。