画线段图解应用题(二)

用图解法解应用题（一）例1乐乐比丫丫大5岁，洋洋比乐乐小2岁，那么丫丫和洋洋相差多少岁？【分析】根据题意，我们可以画一个线段图：很明显，丫丫和洋洋相差5－2＝3岁。

例2朝阳学校三年级四班开展集邮活动，阿呆有92张邮票，笨笨有54张邮票。

问阿呆给笨笨多少张邮票，才能使两人的邮票数相等？【分析】从下面的线段图可以清楚地看到：阿呆给笨笨的邮票数，是阿呆与笨笨邮票的相差数的一半，因此要求本题的解，只要将他们邮票的相差数平均分成两份，每一份就是阿呆给笨笨的邮票数。

（92－54）÷2＝19（张）即阿呆要给笨笨19张邮票，才能使两人的邮票数相等。

通过例2的分析，可以看出画线段图既能充分一线出题中的已知条件，又能形象地把数量关系展示出来，帮助我们很快地找到解题的捷径。

例3把两块一样长的木板像右图这样钉在一起，成了一块木板。

如果这块钉在一起的木板长120厘米，中间重叠部分是16厘米。

这两块木板各长多少厘米？【分析】把长度相等的两木板的一端钉起来，钉在一起的长度部分就是重叠部分，重叠的部分是16厘米，所以这两块木板的总长度是120＋16＝136（厘米），每块木板的长度就是136厘米的一半。

【解】（120＋16）÷2＝68（厘米）答：这两块木板各长68厘米。

【诀窍】类似这样的问题，是要把重复的部分再加一次，求出原来没有重复大的总长度。

当你觉得这样的问题不知如何思考的时候，可以先画出图，借助图形进行思考是一种很好的办法。

例4兄弟俩的年龄和是35岁，哥哥比弟弟大5岁，问哥哥和弟弟各多少岁？【分析】还是用线段图来帮助我们分析：从图中观察出，如果从35岁中去掉5岁，就可以得到两个弟弟的年龄，而列式得：（35－5）÷2＝15（岁）（弟弟的岁数）15＋5＝20（岁）（哥哥的岁数）验算：15＋20＝35（岁）20－15＝5（岁）所以哥哥的年龄是20岁，弟弟的年龄是15岁。

还可以这样分析，如果35岁加上5岁，就可以得到两个哥哥的年龄，则：（35＋5）÷2＝20（岁）（哥哥的岁数）20－5＝15（岁）（弟弟的岁数）例5陈红喜爱集邮，她的中国邮票枚数是外国邮票的3倍，中国邮票比外国邮票多86枚。

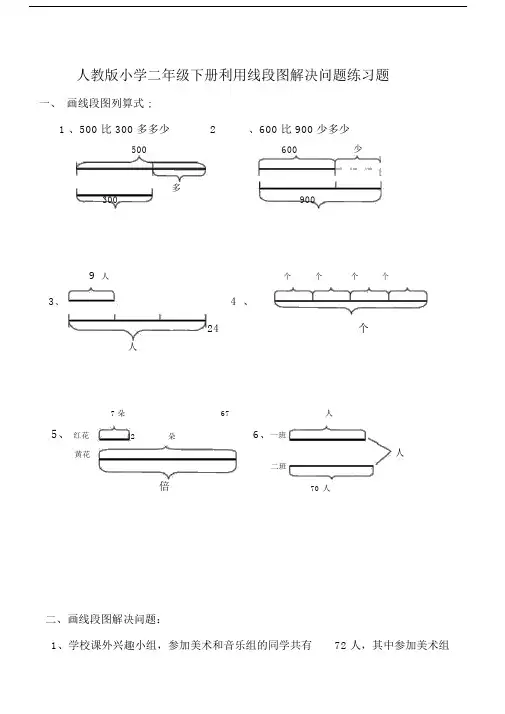
人教版小学二年级下册利用线段图解决问题练习题
一、画线段图列算式 ;
1 、500 比 300 多多少
2 、600 比 900 少多少
500 600 少
多
300900
9 人个个个个
3、 4 、
24 个
人
7 朵67 人
5、红花42 朵
6、一班
黄花人
二班
倍70 人
二、画线段图解决问题：
1、学校课外兴趣小组，参加美术和音乐组的同学共有72 人，其中参加美术组
的同学比音乐组的少 6 人。

参加美术、音乐兴趣小组各有多少人
2、甲乙两桶油共重 82 千克，如果从乙桶倒 2 千克油放入甲桶，则乙桶还比甲桶多 2 千克油。

求甲乙两桶油原来各有多少千克
3、小明与爸爸的岁数和是40 岁，爸爸的岁数是小明的 4 倍。

小明和爸爸各自的岁数是多少
4、李爷爷家养的鸭比鹅多18 只，鸭的只数是鹅的 3 倍。

你知道李爷爷家养的鸭与鹅各多少只吗。

利用画线段图，巧解小学数学难题，运算能力提高一倍，值得收藏在小学数学中，有不少的难题，学生抓耳挠腮，百思不得其解。

这是因为小学生理解能力较差，不会审题，对于题目给出的条件，没有全面、综合去考虑。

结果，得不出正确的解法。

有没有一种巧妙的方法，能让小学生直观地去解题呢？有！那就是利用画线段图来解。

因为线段图非常简洁非常直观明了，通过观察，小学生能够容易地判断出解法，并能通过这种方式，提高自己的分析能力。

举例子来说明吧：两个小同学折纸鹤，小红折的数量比小丽的3倍还多5个，她俩一共折了53个，问题，两个人分别折了多少个？这道题，初看之下，条件有三个，小学生很容易被3倍还多5个这句话给绕住，那么，就可以动手画个线段图，来帮助理解。

看这个线段图，一目了然，学生会马上明白，这道题应该用53－5，得出的结果再平均分成四份，其中的一份就是小丽折的个数，那么小红的也能很容易计算出来了。

再比如这道题：小明买3支笔用了27元，那么，买同样的8支笔，需要多少元？我们继续用线段图来解，如下图：学生一看，就明白了，27元买了三个，先算出一个的价格，再去算8个的价格。

再来看一道复杂一些的分数应用题：某工程队修一条路，前5月修了20千米，正好修了全长的四分之一，照这样计算，剩下的路，需要修多长时间？怎么解呢？依旧用画线段图的方法。

来看看线段图，算法是不是呼之欲出呢！总结一下，如何使用画线段图这种数学方法？使用画线段图需要注意些什么呢？画线段图是一种有效的解决数学问题的方法，可以把复杂的数量关系变的简单易懂，尤其是对于理解能力较弱的同学，使用这一方法更有效。

在使用当中，首先要搞清所有的条件和数量关系，其次，在画图时，还应注意以下几点：第一个，线段的长短得适中，不用太长，只要能等量地表示出数量关系即可。

最好用尺子按照刻度去画，不要画的太随意了。

第二个，画出图以后，得标明数量和条件，像上面的三幅图中，都逐一标明了每一个数量关系，甚至问题也用问号来表示。

六年级画线段图练习题[正文]画线段图是小学数学中的一项基本技能，它能帮助学生更好地理解和掌握几何知识。

今天，我们将介绍一些六年级画线段图练习题，帮助学生巩固这项技能。

练习题一：请根据给出的坐标，画出线段AB并计算其长度。

A(2, 4)，B(6, 8)【解答】首先，在坐标平面上标出点A和点B。

然后，用直尺将点A和点B连线，得到线段AB。

线段AB的两个端点分别是A和B。

最后，使用勾股定理来计算线段AB的长度。

根据勾股定理，线段AB的长度为√[(x2 - x1)² + (y2 - y1)²]。

代入坐标得：√[(6 - 2)² + (8 - 4)²] = √[(4)² + (4)²] = √[16 + 16] = √32 ≈ 5.66所以线段AB的长度约为5.66。

练习题二：已知点C的坐标为(3, 7)，点D的坐标为(3, 1)，请你画出线段CD并计算其长度。

【解答】根据给定的坐标，在坐标平面上标出点C和点D。

然后，用直尺将点C和点D连线，得到线段CD。

线段CD的两个端点分别是C和D。

最后，使用勾股定理计算线段CD的长度。

根据勾股定理，线段CD的长度为√[(x2 - x1)² + (y2 - y1)²]。

代入坐标得：√[(3 - 3)² + (1 - 7)²] = √[(0)² + (6)²] = √[0 + 36] = √36 = 6所以线段CD的长度为6。

练习题三：请根据给出的长度，找到合适的点坐标并画出线段。

线段EF的长度为5，E点的坐标为(2, 3)。

【解答】首先，在坐标平面上标出点E。

然后，选取一个长度为5的尺子，以点E为起点，利用尺子的刻度，在平面上找到距离E点长度为5的位置，标记该位置为点F。

最后，将点E和点F用直尺连起来，得到线段EF。

练习题四：请根据已知条件，找到合适的点坐标并画出指定长度的线段。

小学数学线段图练习题在小学数学中，线段图是一种重要的图形工具，用来表示数字之间的关系和比较。

通过线段图的练习，学生可以巩固和提升对数学概念的理解和运用能力。

以下是一些小学数学线段图练习题，帮助学生加深对线段图的认识和运用。

题目一：水果销售比例某个水果摊位上有三种水果：苹果、橙子和香蕉。

某一天，摊主售出了150个苹果、200个橙子和100个香蕉。

现在，请你根据这些数据完成下述线段图。

解答：首先，我们需要确定线段的刻度。

假设每个小刻度代表10个水果。

然后，我们根据售出数量在线段上标出相应的长度。

最后，根据线段的长度比较，我们可以得出销售比例。

请注意，线段图的比例要和实际销售数量的比例相符。

在这个例子中，我们可以看到苹果、橙子和香蕉的销售比例分别为3∶4∶2。

这意味着橙子的销售量最多，苹果次之，香蕉最少。

题目二：班级成绩对比某个班级有30个学生，他们的数学成绩如下所示：小明：85 小红：90 张三：75 李四：80 王五：95...（省略部分学生成绩）现在，请你根据这些数据完成下述线段图。

解答：同样地，我们需要确定线段的刻度。

根据刻度选择的不同，线段图的形状也会有所不同。

在这里，让我们尝试每个小刻度代表5分。

根据学生的成绩，在线段上标出相应的长度。

通过比较线段的长度，我们可以看出谁的成绩更好或更差。

这个例子中，我们可以看到小红的成绩最高，王五次之，李四、小明的成绩相当，而张三的成绩最低。

通过线段图，我们可以清楚地了解到每位学生的数学成绩在班级中的位置。

题目三：每日步数目标请你制作一个线段图，帮助小明追踪他一周内的每日步数目标完成情况。

星期一：5800步星期二：6100步星期三：5200步星期四：6600步星期五：5900步星期六：6000步星期日：5400步解答：我们可以根据小明每日的步数目标和实际达成的步数，在线段上标出相应的长度。

通过比较线段的长度，我们可以了解小明在每天达成目标的情况。

通过线段图，我们可以看到小明在星期一和星期三的步数没有达到目标，而在星期四和星期六的步数超过了目标。

画图法解应用题苏联教育家苏霍姆林斯基曾经说过：“如果哪个学生学会了画应用题，我就可以有把握地说，他一定能学会解应用题。

”可见，画图对于小学数学解决问题的重要性。

在解答一些应用题时，用作图法可以把题目的数量关系揭示出来，以其形象、直观的特点，使题意一目了然，对解答条件隐蔽，复杂疑难应用题，能起到化难为易，化繁为简的作用，从而有助于快速找到解题的途径，有效地提高学生的自我学习能力和创新能力，使学生学会学习。

作图法解应用题中，常见的数学图有以下几种：一、线段图线段图是由几条线段组合在一起，用来表示应用题中的数量关系，帮助人们分析题意，解答问题的一种平面图形。

线段图在小学数学应用题学习中它可以帮助学生轻松地解答复杂关系的应用题，强化数量关系的表述训练，能根据数量关系有序地进行解题演练。

举例：欢欢和喵喵共有25个本子，如果欢欢用去了3个本子，喵喵买回2个本子，那么她们的本子就一样多了，你知道她们原来各有本子多少个吗？列式计算：喵喵 (25－3－2)÷2＝10(本) 欢欢 25－10＝15(本)二、树形图在解答应用题时，我们常常采用枚举法把所有符合题目条件的对象一一列举出来。

我们采用画树形图的方法，借助树的分叉特征构造出的树形图可以对数学问题中有可能出现的多种可能逐一例举出来，不仅形象直观，而且有条理又不易重复或遗漏，使人一目了然，有助于作出正确的判断。

举例：一个口袋中装有红、白、绿三只小球，另一只口袋中装有红、白两只小球。

现从两只口袋中各取一只小球，求两只小球颜色一样的概率是多少？从图中可以看出，两只小球颜色搭配的可能性共6种，而两只小球颜色一样的可能性只有(红-红)，(白-白)共2种，所以两只小球颜色一样的概率为三分之一。

三、集合图在数学中，经常用平面上封闭曲线的内部代表集合，以及用以表示集合之间的关系，这样的图形称之为“集合图”。

举例：参加跳绳的有6人，参加踢毽子的有7人，两项都参加的有3人，这个组共有几人？6＋7－3＝10（人）四、情景图把复杂的数学问题用简单的图画表示，把情景再现出来，让人有身临其境的感觉，便于学生理解和分析应用题。

方法技巧练——利用线段图解决问题
1.甲、乙两列火车同时从相距450千米的两地相向行驶,甲车每小时行驶45千米,5小时后两车相距25千米(相遇前),乙车每小时行驶多少千米?
想:可以先画线段图表示出题目中的数量关系。

线段图:
乙车每小时行驶的路程为25千米
等量关系:甲车每小时行驶的路程×5+()×5+()=450千米。

其中(乙车每小时行驶的路程)是未知数。

解:设乙车每小时行驶x千米。

(列方程并解方程)
45×5+5x+25=450
5x=450-250
x=40
答:乙车每小时行驶40千米。

2.合唱队的人数是舞蹈队的3倍,如果从合唱队调入舞蹈队14人,那么两个队的人数相等,舞蹈队有多少人?(画线段图并列方程解答)
解:设舞蹈队有x人。

x+14=3x-14
x=3x-28
x=14
答:舞蹈队有14人。

3.如果从一班调1名学生到二班,那么一班和二班的人数相等;如果从二班调1名学生到三班,那么三班比二班多2人。

一班和三班相比,哪个班人数多?多几人?
一班人数最多,多2人。

4.有甲、乙、丙三桶油,若从甲桶倒入乙桶1.2千克,则两桶油的质量相等,若从乙桶倒入丙桶2千克,则丙桶比乙桶多1千克,已知丙桶有5千克油,你能求出甲桶有多少油吗?
解:设甲桶有油x千克。

x-1.2=5+2-1+2+1.2
x-1.2=9.2
x=10.4
答:甲桶有10.4千克油。