边坡大变形弹塑性有限元分析
- 格式:pdf
- 大小:221.35 KB
- 文档页数:5





136大型复杂结构焊接变形热弹塑性有限元分析纪浩然(SEW-工业减速机(天津)有限公司,中国 天津 300457)摘 要:随着科学技术与信息技术的飞速发展与的不断完善,机械设计制造技术得到快速发展,从而促进了机械设计制造控制技术在各个生产领域的应用,同时对设计方法和实现工艺的要求越来越高。
由于焊接标准的提高以及平台工作要求的提升,为了提高了设计的科学性与合理性,保证结构设计和产品功能的相辅相成,通过空间钢架梁组合模型全面地评估改造方案的总体屈服屈曲强度,对大型复杂结构焊接变形热弹塑性问题进行分析。
基于此,文章从多个角度大型复杂结构焊接变形热弹塑性有限元进行深入分析,希望对相关人员提供参考。
关键词:大型复杂结构;焊接变形;热弹塑性有限元;分析中图分类号:U671.8 文献标识码:A 文章编号:11-5004(2019)03-0136-2收稿日期:2019-03作者简介:纪浩然,男,汉族,天津人,本科,机械设计制造中级,研究方向:机械设计制造。
在科学技术与信息技术飞速发展的时代背景下,对机械设计尤其是工业设计提出了严格要求。
在信息技术高速发展的时代背景下,有限元软件逐渐被应用到机械制造领域中。
根据钢架梁理论以及基础设计原理,对大型复杂结构采用组合焊道,建立三维有限元模型,由于多方面因素的限制还需要对大型复杂结构焊接变形热弹塑性的技术方案进行不断优化。
文章从几个角度就大型复杂结构焊接变形热弹塑性有限元进行深入分析,预测结构的焊接变形,为业内平台的设计与改造提供数据支持。
1 大型复杂结构焊接变形问题分析随着焊接工艺与科学技术的不断提高,对金属产品的需求量与日俱增,这几年,制造企业得到快速发展,使得机械产品市场变得更加复杂、多变,市场竞争越来越激烈。
随着技术的进步和质量管理水平的不断提高,大型复杂结构焊接的可靠性也得到提高,但是在应用过程中还存在诸多问题,市场竞争恶劣,安全事故频频发生,企业管理不科学、不规范,经济效益与社会效益都不理想。

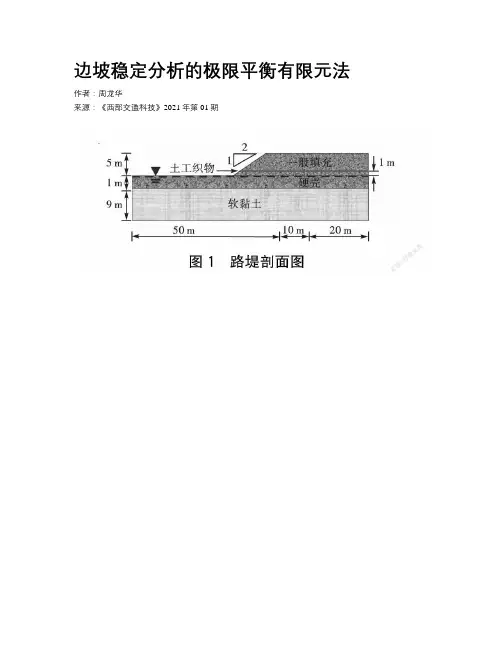
边坡稳定分析的极限平衡有限元法作者:***来源:《西部交通科技》2021年第01期摘要:极限平衡软件SLOPE/W和有限元程序PLAXE是目前岩土工程中常用的两种软件程序。
采用极限平衡法进行边坡分析时,需要将地面划分为若干垂直层面,并使用静态平衡方程计算各层面的安全系数(FOS)和应力,而有限元法则需要输入土的性质和单元的弹塑性参数。
文章比较了有限元法和极限平衡法在边坡稳定性分析中的应用,讨论了各种方法的适用性和局限性,并评估了边坡稳定性分析模型输出的实用性,可为边坡稳定性评估提供可靠依据。
关键词:有限元法;极限平衡;边坡稳定性中图分类号:U416.1+4文献标识码:ADOI:10.13282/ki.wccst.2021.01.022文章編号:1673-4874(2021)01-0078-030引言随着对基础设施和自然资源需求的不断扩大,对工程开挖和道路建设的要求也越来越高。
在工程建设过程中,山体滑坡和地震等自然灾害是岩土工程师和地质学家面临的重要问题。
边坡的稳定性是施工前、施工中、施工后各利益相关者共同关心的重要问题,如果要改变边坡稳定技术,安全系数(FOS)的微小差异可能导致施工成本的巨大差异。
这一点很重要,因为目前还没有明确的证据表明,哪种方法能产生最可接受的结果[1-3]。
与基础设施有关的土质边坡失稳是一个持续存在的问题,因为边坡破坏危及公共安全并导致昂贵的修复工作。
近几十年来,人们开发了一系列功能强大的边坡稳定分析设计软件包。
这些程序包括边坡稳定分析的极限平衡法和有限元法。
极限平衡法有许多局限性和不一致性,但被认为是最常用的方法。
随着技术进步,有限元程序简化了边坡稳定性分析。
SLOPE/W和PLAXIS是目前岩土工程师使用的两种常用软件程序。
SLOPE/W和PLAXIS分别用于极限平衡法和有限元法,每一个程序都被用来确定边坡的安全系数及其随后的设计要求。
根据所需的信息,分析和比较每个程序的结果将有助于确定哪个程序更准确。

三维边坡稳定弹塑性有限元分析与评价
边坡是地质结构特殊的体系,其不平衡情况受到多种因素的影响,从而影响边坡的稳定性。
为了研究边坡稳定性问题,综合考虑地质、力学以及环境因素,需要采用三维弹塑性有限元方法(FEM)进行分
析与评价。
弹塑性有限元分析法是以极限状态理论为基础的一种分析方法。
它将复杂的构造系统抽象为一系列有限数量的单元,每个单元由一个拟合变形的弹性-塑性曲线描述。
基于此模型,可以研究边坡的三维
结构及剪力传播规律,评价边坡的稳定性。
在三维弹塑性有限元分析与评价过程中,应首先建立三维边坡模型,并根据边坡材料特性及应力状态,选定有限元单元及模型参数。
接着,根据自重及外力因素,求取边坡体系的力学参数,它可以表征边坡体系的动力学特性,它的大小关系将影响边坡的稳定性。
最后,根据计算出的力学参数,判断边坡的稳定状态,以评估边坡稳定性。
基于三维弹塑性有限元方法,可以准确地模拟边坡的构造结构,反映边坡体系的实际性能,从而有效评价边坡稳定性。
但是,这种方法仍有若干弊端。
首先,由于有限元中所使用的参数均为理论值,无法很好地反映边坡实际情况,无法准确预测边坡的稳定程度。
其次,边坡的三维模型建立过程繁琐,需要大量的计算工作,且耗时较长。
此外,由于边坡体系中的地质环境、力学条件及实际应用施工工艺等等因素,均会影响边坡的稳定性,因此,需要考虑这些因素,完善模型,以便更好地评价边坡稳定性。
综上,三维弹塑性有限元分析是一种准确、可靠的评价边坡稳定性的方法,但仍需遵循科学的方法,完善模型,以便更好地提高分析与评价边坡稳定性的准确性。



三维边坡稳定弹塑性有限元分析与评价边坡的稳定性对环境的稳定性与可持续发展具有重要意义,而三维边坡稳定弹塑性有限元分析与评价技术则可更有效地维护边坡稳定性。
本文重点介绍了三维边坡稳定弹塑性有限元分析与评价,分析其基本原理、数学模型、常见应用等内容,并针对有限元分析技术存在的广泛应用、空间技术局限性等问题,提出若干改进的方法和技术。
一、三维边坡稳定弹塑性有限元分析学术回顾三维边坡稳定弹塑性有限元分析是以数学模型为基础,运用有限元法进行地质边坡稳定性的分析与评价的技术,结合有限元求解,分析边坡的稳定性。
其基本原理是:当地质边坡受力时,其受力状态下的变形可以用位移量、应变量或应力量来描述,而每一点受力状态的变形均可用一组局部坐标表示,当受力后的变形状态下的变形强度比受力前的状态还要低时,就可以判断为无滑移状态,也就是稳定。
三维边坡稳定弹塑性有限元分析迎合了边坡稳定性分析中几何形态复杂、多尺度、考虑材料弹塑性、力学性质复杂等复杂性因素,精确地模拟了边坡稳定性分析过程中的复杂动力学过程。
二、常见应用三维边坡稳定弹塑性有限元分析技术有多种应用,主要应用于岩土体结构的受力数值模拟、岩土体的变形和失稳的有限元模拟和分析、及岩土体稳定性的评价。
在岩土体受力数值模拟方面,三维边坡稳定弹塑性有限元分析技术可以通过计算机化的方法,对边坡受力数值模拟和变形和失稳的有限元模拟分析,分析受力后的位移、变形和强度,从而更好地评价岩土体结构的受力稳定性。
此外,三维边坡稳定弹塑性有限元分析技术可以运用于地质模型结构的有限元模拟,对模型进行受力和变形分析,验证建模中存在的错误,并对工程建设中可能出现的风险进行预测,提出具体意见。
三、改进思路物理模拟的三维边坡稳定弹塑性有限元分析具有计算量大,计算时间较长,技术局限性等缺点,因此,提出若干改进措施可以有效改善这些问题,提高有限元分析技术的精度和应用效果:(1)布置边坡滑移状态时,尽量采用体单元网格布置,而不是采用梯度布置的网格。
三维边坡稳定弹塑性有限元分析与评价作为地质现象而持续发展的坡面稳定性是一个严峻的问题,它受人类影响,增加了地质灾害发生的可能性。
因此,坡面稳定性评价应成为重要的工程项目之一。
近年来,计算机技术的发展,使得边坡稳定性分析和评价变得更加容易和可行。
其中有一种极具效率的计算机技术是三维边坡弹塑性有限元分析(FiniteElementAnalysis,FEM)。
三维边坡弹塑性有限元分析是一种用于研究坡面及其周围的地质结构的有力的工具。
这一分析方法把坡面的空间构造划分为若干相交的有限元,比如三角形和形状尖角四边形,并在每个元素中计算它们的变形、应力和位移。
有限元分析可以详细研究坡面的受力状态,从而对稳定性进行更准确的分析和评价。
FEM技术的主要优点之一是能够模拟坡面的实际变形运动,得出与实际状况一致的结果。
它可以有效地计算每个有限元的变形及其相互之间的关系,从而准确地模拟每个坡面元素的稳定性及其受力状态,以判断是否发生坍塌等突变性状态。
此外,由于FEM技术可以以计算机记录数据,重复计算时不需要重新完成,它也可以有效地评估每个坡面中受力情况的变化。
三维边坡弹塑性有限元分析技术为边坡稳定性的分析和评价提供了很大的便利。
在坡面发展初期,可以利用FEM技术对坡面的设计及其施工过程进行相对准确的计算和分析,从而确保坡面的稳定性和延续性。
有限元分析还可以帮助在边坡发展后期,提出有效的稳定性评价和加固措施,以降低边坡发生滑坡等地质灾害的可能性。
因此,三维边坡弹塑性有限元分析是一种高效的坡面稳定性分析技术,它可以有效地计算坡面的受力及其可能发生突变性状态,并有效地评估坡面稳定性,从而确保坡面稳定性。
为此,FEM技术正在被广泛应用于边坡稳定性的分析和评价,并且在未来可能会发挥更大的作用。