当前位置：文档之家 › 弹塑性变形与极限载荷分析

弹塑性变形与极限载荷分析

  • 格式：pdf
  • 大小：643.58 KB
  • 文档页数：25

下载文档原格式

  / 25

合集下载

塑性分析和极限荷载

塑性分析和极限荷载


三、基本假设 1、材料为“理想弹塑性材料” 。 、材料为“理想弹塑性材料” 2、拉压时，应力、应变关系相同。 、拉压时，应力、应变关系相同。 3、满足平截面假定。即无论弹、塑性阶段，保持平截面不变。 、满足平截面假定。即无论弹、塑性阶段，保持平截面不变。
σ
σy
卸载时有残余变形
ε
§12-2 纯弯曲梁的极限弯矩和塑 性铰
（4）极限状态 ）
2、确定单跨梁极限荷载的机动法 、
q
l
qu
A
θ
xθ
Mu x
l θ 2
2θ
θ
B
dx C
Mu
Mu
临界状态时， 临界状态时，由虚功方 程： 2∫ xθ ⋅ qu dx = M u ⋅ θ + M u ⋅ θ + M u ⋅ 2θ
1 2 l θ ⋅ qu = 4 M uθ 4 16 M u qu = ∴ l2
1. 弹性阶段
b b 2 2
z h 2 h 2
M
M
σ = Eε
Ms σs = 1 2 bh 6
ε =κy
1 M s = bh 2σ s 6
κ= κs =
ε
y h/2 = 2σ s Eh
σs / E
y
σs
h 2 h 2
2.弹塑性阶段
y σ = σs y0
y
κ =
εs
y0
=
σs
Ey0
=
h κs 2 y0
p
机构4 机构
p
q = 2p
p1 = 2.5
Mu a
1.2 p
θ
Mu
Mu
θ 2θ
pu = 1.33
Mu a
结构力学结构的塑性分析与极限荷载 ppt课件

结构力学结构的塑性分析与极限荷载 ppt课件

屈服弯矩、极限弯矩 以理想弹塑性材料的矩形截面纯弯曲梁为例：
M
M
随着M的增大，梁截面应力的变化为：
b
s
s
h b
s
h
y0 y0
s
s
a)
b)
s c)
b
s
s
s
h
y0 y0
s
s
a)
b)
s c)
图a）弹性阶段，最外纤维处应力达到屈服极限σs ，弯矩M
为：
MS
bh2 6
s
→屈服弯矩
图b）弹塑性阶段，y0部分为弹性区,称为弹性核。
图c）塑性流动阶段，y0→0。相应的弯矩M为：
Mu
bh
s
→极限弯矩
是截面所能承受的最大弯矩。
极限弯矩的计算
Mu
bh
s
设塑性流动阶段截面上受压区和受拉区的面积分别为A1
和A2，并且此时受压区和受拉区的应力均为常量，又因为
梁是没有轴力的，所以:
sA1sA20
A1A2A/2
可见，塑性流动阶段的中性轴应等分截面面积。
【例17.1 】 图示为矩形截面简支梁在跨中承受集中荷载，试 求极限荷载。
FP
FPu
已知Mu
解：
FPul
Mu
FPu
Mu l
可破坏荷载： 对于任一单向破坏机构，用平衡条件求得的荷载值，称
为可破坏荷载，常用FP+ 表示。
基本定理：
（1）唯一性定理：极限荷载FPu值是唯一确定的。
（2）极小定理：极限荷载是可破坏荷载中的极小者。
由此，极限弯矩的计算方法: M u s(SS)
S、S分别为面 A、 积 A对等面积轴的静矩
弹塑性力学之结构的塑性极限分析

弹塑性力学之结构的塑性极限分析

25
塑性极限载荷
4"6
确定塑性区位置
截面的上下两塑性区相连，使 跨中左右两截面产生像结构
・特点:
-塑性较的存在是由于该截面 上的弯矩等于塑性极限弯矩; 故不能传递大于塑性极限弯 矩的弯矩。
<]
ax(x9z\ay=az= rxy=ryz= rzx=0
♦:・小挠度假设：在梁达到塑性极限状态瞬 间之前，挠度与横截面尺寸相比为一微 小量，可用变形前梁的尺寸进行计算。
二.弹性阶段
—
P1
6M
♦ Mises屈服条件:
xmax
bh2
弹性极限弯矩
二
2bh2
弹性极限载荷
三.弹塑性阶段（约束塑性变形阶段）
>Mp塑性区扩展
第十章结构的塑性极限分析
矗塑性极限分析定理和方法
❖梁的极限分析❖圆板的极限分析
❖梁模型法计算圆板和环板的塑性极限 載荷
§10-1梁的弹塑性弯曲
1.基本假定
•:•平截面假设：在变形过程中，变形 前为平面的横截面，变形后仍保持 为平面，且与变形后梁的轴线垂直。
z5=— P
・纵向纤维互不挤压：不计挤压应力， 横截面上只有正应力。
heh/2
陆=2町(yxzdz+ 2町aszdz
0he
陆
0叽he
“Me
Ms=—-
s2
h2
弹塑性区交界线:
h/2
(Jszdz
陆=
£
弹塑性区交界线：饥=±丄3
h~2\
<]
►P(lΒιβλιοθήκη 2x)2ALPl/4
四.全塑性阶段
X—6
x = 0
塑性极限弯矩
n
A
结构力学第17章结构的塑性分析与极限荷载

结构力学第17章结构的塑性分析与极限荷载


Mu
(
l
) 0
l
得:
FPu
6M u l
[例] 求梁的极限荷载，已知极限弯矩为Mu。
q
qu
A
C
B
l/2
l/2
A Mu
Mu l
C B
2 Mu
解：计算刚体虚功：
2
瞬变体系机构
W
l
y qu dx
Mu
Mu
Mu
qu
(
l
l
)
M u
qu l
M u
虚功方程：
qu l
M u
qu
16M u l2
FPu
M
' u
3 2l
Mu
9 2l
A
M ' u
A
2l /3
FPu
DC
Mu
D
l/3
FPu

l
(M u
M u )
A
3 2l
D
3 2l
3 l
9 2l
弯矩图如图，弯矩
MB=
1 2
(M
' u
Mu )
M
u
,即M
' u
3M u
时，此破坏形态就可实现。
M' u
1 2
(M
' u
-
M
u
)
FPu D
C
A
B
Mu
综上，当M
Mu
FP增大
A
C
B
FP继续增大，第二个塑性铰出现在C 截面，梁变为机构。弯矩 增量图相应于简支梁的弯矩图（如图）。
Mu
FP达到极限值FPu
塑性极限分析

塑性极限分析

两种 不同 材料
内杆进 入塑性
外杆仍 为弹性
外杆“回弹力” 和内杆“抵抗 力”平衡
内杆弹性阶 段已卸完
二、塑性极限分析的概念与假设
1.单调加载：荷载由零开始，按比例同时加到最后值
（避免加载路径的影响）
2.几何线性：结构局部产生塑性变形，整体变形仍足够小
3.几何不变体系与几何可变体系
屈服区小
外力基本不变时，变形 也基本不变的结构体系， 称为几何不变体系。
5. 极限荷载
三根杆均达到 屈服状态时
Fu 2 s Acos s A
1 2cos s A
§3 等直圆杆扭转时的极限扭矩
T
T
一、极限扭矩
1. 弹性—理想塑性模型 2. 屈服扭矩
τ τs
γ
TS
S
WP

d 3
16

S
τs
3. 极限扭矩
T
T
τ τs
γ
可继续加载，已屈服部分应力不变，屈服区向里发展， 直至整个截面全部屈服。
AC AD
例：已知E、A、θ、σs，材料为弹性— B 理想塑性。求Fs、Fu
F
cos2 F
FAD 1 2cos 3 FAC 1 2cos 3
4. 屈服荷载
D
C
θθ A F
FAD A

Fs
1 2cos 3
A s
Fs 1 2cos 3 s A
Mu


s

bh 2

h 4

bh 2

h 4


s
bh2 4
At
Ms
材料力学第十二章-考虑材料塑性的极限分析精选全文

材料力学第十二章-考虑材料塑性的极限分析精选全文


M Hi 0 S A a S A 2a Fu 3a 0
极限荷载 Fu S A 容许荷载 [F ] Fu / n
§2-3 等直圆杆扭转时的极限扭矩
S
Mx
S
Mx
S
Mx
O
外力增大
O
外力增大
O
S
S
S
只有弹性区 弹性极限状态
即有弹性区，又有塑性区 弹塑性状态
只有塑性区 塑性极限状态
弹性状态下横截面上 扭矩的最大值
max－S
残余应力
Mu Mr MS
由残余应力分布图知：
max
Mr Wz
最大残余应力发生在截面屈服区与弹性区的交界处；
中性轴上各点的残余应力为零。
作业：
2－2、5； 2－10
第十二章 考虑材料塑性的极限分 析
◆ 塑性变形·塑性极限分析的假设 ◆ 拉、压杆系的极限荷载 ◆ 等直圆杆扭转时的极限扭矩 ◆ 梁的极限弯矩·塑性铰
§2-1 塑性变形·塑性极限分析的假设
在弹性范围内进行强度计算
单向应力状态下采用正应力强度条件： max [ ] 纯切应力状态下采用切应力强度条件： max [ ]
弹性极限状态
弹塑性状态
屈服弯矩 MS ？
在完全塑性状态下
完全塑性状态
极限弯矩 Mu ？
塑性铰 卸载时塑性铰的效应会消失
弹性极限状态
弹塑性状态
完全塑性状态
弹性极限状态下横截面上的最大弯矩 MS ：
max
M Wz
MS
bh2 6
S
完全塑性状态下横截面上的最大弯矩 Mu ？
截面完全屈服时中性轴的位置如何确定？
M xS
Wp S
πd3 16
结构力学 结构塑性分析的极限荷载

结构力学 结构塑性分析的极限荷载


FP2/2
5FP1/2
5FP2/2
(b) M C M s FP1 FPs (c) M S M C M u FPs FP2 FPu
3FPu Mu
FPu/2
Fpu FPu/2
5FPu/2
(d) M C M u
2FPu
FPu/2
(e)
(1).结构的极限状态
极限荷载是相应于结构极限状态时的荷载。
塑性铰的以下特征：
(1)塑性铰承受并传递极限弯矩Mu。 (2)塑性铰是单向铰，只能使其两侧按与荷 载增加（弯矩增大）相一致方向发生有限的 转动。 (3)塑性铰不是一个铰点，而是具有一定的 长度。
综上所述，截面上各点应力均等于屈服应力 的应力状态、截面达到极限弯矩、截面形成 塑性铰，均表示该截面达到其塑性流动的极 限状态。
即：
(
FP 2 L 4
Mu 2
)
FP L 4
Mu
解得：
FP 2
FP
6M u L
(a)
即：
FPu
6M u L
2)超静定梁的极限荷载
由前已由叠加方法得出了式(a)所示单跨 超静定梁的极限荷载。观察梁的最后极 限 弯 矩 图 (g) ， 既 是 所 叠 加 的 两 弯 矩 图 (c)、(e)的叠加结果。利用梁的极限弯 矩图的平衡条件，可得：
当MC<Mu，FP2<FPu时，梁处于弹塑性发 展阶段，弯矩图见图(c)。 当MC=Mu时，截面C也将首先达到截面的塑 性极限状态，也即形成第一个塑性铰。
结构上出现足够多的塑性铰，能使原结构 成为破坏机构时的状态为结构的极限状态。 结构在极限状态仍能保持静力平衡。
(2)结构的极限荷载
a.极限弯矩平衡法 由静力平衡条件得：
第五章 极限分析法全

第五章 极限分析法全


V Fiuip* dV
V
p* p* ij ij
dV
SD c vtp* d S
反证法：
假设由上式确定的荷载Ti，Fi小于极限荷载，则可找 到与之平衡的静力场σijE，于是可得到虚功率方程
S Tiuip* d S
V Fiuip* dV
E p*
V ij ij
dV
SD
n tan
vtp* d S
虚功原理表明：对于一个连续的变形体，静力容许的应 力场在机动容许的位移场上所作的外(虚)功。虚功率方程可 表示为：
静力容许
S Ti*vi* d S
V Fivi* dV
V
* *
ij ij
dV
机动容许 左端表示外力(面力和体力)的虚功率，右端表示虚变形功率。
现证明如下： 将应力边界条件 Ti* i*jnj 代入虚功率方程左端的面积分 部分，并利用高斯积分公式，可得
W Dlh n tanlh p n tanlvcos
v cos 就是间断面相对速度在切线方向的分量，可记为 vt
于是可以得到Coulomb材料沿速度间断面Sl的能量消散率
W Si n tan vt d Si
当φ=0，上式就蜕化成
W
Si
vit
d Si
当速度间断面上的应力为屈服应力时：
由于真实应力场一定是静力容许的应力场，所以极限
状态时的虚功率公式
S Tivi d S
V Fivi dV
V ij ij dV
c
SD
vt
dS
S Ti*vi* d S
V Fivi* dV
* *
V ij ij
dV
Si n tan vt d Si
结构塑性分析与极限荷载

结构塑性分析与极限荷载


bh Mu s 4
这是截面所能承受的最大弯矩， 称为极限弯矩。
显然，对于 矩形截面极限 弯矩是屈服弯 矩的1.5倍。
12
σs h b y z σs
σs y0
σs

1)弹性阶段（b） 2)弹塑性阶段（c）
3)塑性阶段(d)
σs

σs

（d）
（a）
（b）
（c）
极限弯矩是整个截面达到塑性流动时截面所能承受的最 大弯矩。它主要与σs和截面形状尺寸有关，剪力对它的 影响可忽略不计。
注：应力的单位用（Pa），长度单位用（m），力的单位用 （N），弯矩单位（N.m）
20
M u 240 80 20 50 20 40 20 2 46080000N .m m) 46.08(kN.m) (
注：应力的单位用（MPa），长度单位用（mm），力的单 位用（N），弯矩单位（N.mm）
20
例：设有矩形截面梁受 载如图所示，试求极限 荷载F P u。 解：方法一—平衡法
A l
FP
B
l
C
（1）作M图（图b）。 由M图可知：在极限荷载 作用下，塑性铰将在C处 形成，此时，Mc=M u
Mu
FPu l 4
（2）由静力平衡条件，求F P u 对极限状态，由梁的平衡，得：
FPul / 4 Mu
塑性阶段时当σmax=[σ] ，结构并没有破坏，也就是
说，并没有耗尽所有的承载能力。 弹性设计没有考虑材料超过屈服极限后结构这一 部分的承载能力，弹性设计法不能正确地反映整个结 构的安全储备，因此弹性设计是不够经济合理的。
4
§16-1 概 述
3、塑性设计 ——把结构破坏时能承受的极限荷载除以荷载系数， 得到容许荷载，并以此为依据进行设计。即： Fpu 式中：FP——结构实际承受的载荷； Fp Fp FPu——极限载荷； k k ——荷载系数。 塑性设计特点： 是以理想弹塑性材料的结构体系为研究对象，从整 个结构所能承受的荷载来考虑，充分利用了材料的承 5 载能力，更经济合理。
结构力学 结构的塑性分析与极限荷载

结构力学 结构的塑性分析与极限荷载


A l/3
FPu
B
DC
Mu
B
Mu
D
l/3
l/3
B
3 l
D
6 l
此时M图如图，MA=3Mu
3M u
Mu
A
B
l/3 l/6
FPu
D
C
Mu
当3M u M u，此破坏可实现。
由虚功方程可得： FPu MuB MuD
FPu
Mu
(3 l
6) l
FPu
M u l
2 当截面D和A出现塑性铰时的破坏机构
FPu Mu' A MuD
极限荷载
q 2l x 2M u x(l x) l
qu
22 3 24
Mu l2
11
.7
Mu l2
极限荷载复习题
1. 极限分析的目的是什么？ 答：寻找结构承载能力的极限，充分利用材料。
2. 试说明塑性铰与普通铰的异同。 答：当截面弯矩达到极限弯矩时，这种截面可称为塑性铰； 塑性铰是单向铰，塑性铰只能沿弯矩增大的方向发生有限的 转角；塑性铰可传递弯矩，普通铰不能传递弯矩。
屈服弯矩、极限弯矩 以理想弹塑性材料的矩形截面纯弯曲梁为例：
M
M
随着M的增大，梁截面应力的变化为：
b
s
s
h b
s
h
y0 y0
s
s
a)
b)
s
c)
b
s
s
s
h
y0 y0
s
s
a)
b)
s
c)
图a）弹性阶段，最外纤维处应力达到屈服极限σs ，弯矩M
为：
MS
bh2 6
材料力学考虑材料塑性的极限分析

材料力学考虑材料塑性的极限分析


则极限弯矩为
由
bh2 Mu s s 4
bh2 ss Mu 42 1.5 M s bh ss 6
可见，考虑了材料塑性，
矩形截面梁对应的弯矩极限值可以增大 50％。
几种常用截面的 Mu/Ms 比值见下表。
表 1 几种常用截面的 Mu/Ms 比值
截面形状
M u / Ms
1.15-1.17
1.27
πd 3 Ts Wp s s 16
s
(a)
若继续增大扭矩，则随着切应变增大，此直径上 各点处的切应力将从周围向中心逐渐增大到 s 。
s
(b)
当截面上各点处的切应力均达到 s , 整个截面进 入完全塑性状态。这时不需要再增大外力偶矩，圆杆 将继续扭转变形，即扭杆达到极限状态。对应的极限 扭矩为：
q (a) A
l
解：先按弹性分
B
4l 9
8 ql 2 81
l 3
C b (b) ql 2 18
h
析的方法作出梁
的弯矩图 （图c） 得出最大弯矩为
8ql2 M max 81
(c)
当梁达到极限状态时，其最大弯矩等于极限弯矩， 梁上的荷载达到极限值。 即
8qu l 2 bh2 Mu s sWs s s 81 4
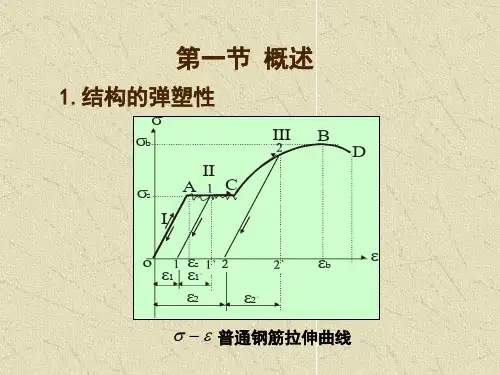
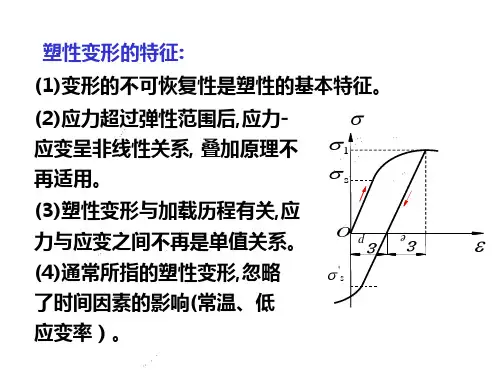
塑性变形的特征:
(1)变形的不可恢复性是塑性的基本特征。
(2)应力超过弹性范围后,应力应变呈非线性关系, 叠加原理
s
s1
不再适用。
(3)塑性变形与加载历程有关,应 力与应变之间不再是单值关系。 (4)通常所指的塑性变形,忽 略了时间因素的影响(常温、 低应变率）。
ss
O
e p ee
e
s 's

结构力学15第十五章.结构的塑性分析与极限荷载

2
内力虚功
Wi Mu Mu 2 Mu 4Mu
由We=Wi，可得
所以有
1 2 qu l 4 M u 4
16 M u qu l2
16
例15-3-3 求梁的极限荷载，已知梁截面极限弯矩 为Mu。 q 解: 塑性铰位置：A截面及跨 A l 中最大弯矩截面C。 qu 整体平衡 M A 0
有当 1 ( M u' M u ) M u ,即M u' 3M u 时，此破坏 2 FPu 形态才可能实现。
FPu M A M u D
' u
A
3 9 FPu M Mu 2l 2l
' u
M u' A 2l /3
A
3 2l

D Mu
C
D
l /3
3
二、材料的应力——应变关系
在塑性设计中，通常假设材料为理想弹塑性， 其应力与应变关系如下：

s A
C B

s A
C
B
o
εs εP εs ε
D
ε
o
εs
ε
D
a) 理想弹塑性模型
b) 弹塑性硬化模型
4
1）残余应变
当应力达到屈服应力σs后在C点卸载至D点， 即应力减小为零，此时，应变并不等于零，而 为εP，由下图可以看出， ε= εs+ εP， εP是应变 的塑性部分，称为残余应变。
一、 极限弯矩
下图示理想弹塑性材料的矩形截面纯弯梁， 随着M 增大，梁会经历由弹性阶段到弹塑性阶 段最后到塑性阶段的过程（见下页图）。无论 在哪一个阶段，平截面假定都成立。
M M h
b

清华大学研究生弹塑性力学讲义 10弹塑性_结构的塑性极限分析与安定性


(13)
应该注意到，此式似乎是相应于机动场的应力
σ
* ij
、切向速度间断线上的剪应力即剪切
屈服应力τ s 、和给定面力 ti * = η∗ti 与机动场的应变率和速度场的虚功率方程，实际上并 不是。其中的应力与面力并不构成静力许可状态。其实，只有和任意机动场均满足虚
功率方程的应力和外力才一定是静力许可的，只和某种机动场满足这样的方程的应力
一、塑性极限状态和界限定理
z 极限状态和极限分析 结构弹塑性分析一般要跟踪加载和变形历史。如果忽略材料的塑性强化特性（即
采用理想塑性模型），并忽略物体由变形引起的几何尺寸变化（即采用小变形假设）， 则当外载达到某一定值时，理想塑性体可在外载不变的情况下发生塑性流动，即无限 制的塑性变形。这时称物体（或结构）处于塑性极限状态，简称极限状态；所受的载 荷称为物体或结构的极限承载能力或极限载荷；与之相应的速度场则称为塑性破损机 构，或塑性流动机构。
∫ ∫ ∫ −
V1
σ
ε(s)
ij
&i(jk)dv
+
V1 fi(s)vi(k)dv +
S10 + SD ti(s)vi(k)ds = 0
∫ ∫ ∫ −
V2
σ
ε(s)
ij
&i(jk)dv
+
V2 fi(s)vi(k)dv +
S20 +SD ti(s)vi(k)ds = 0
两式相加即可得到
∫ ∫ ∫ ∫ V
τ
0 n
⎡⎣vt ⎤⎦ ds
(9)
考虑到：外载一定做正功，即
∫ tSt i vi ds > 0
⎯3⎯
第九章 结构的塑性极限分析与安定性

10 梁的弹塑性弯曲与塑性极限分析



塑性极限分析的完全解：
满足平衡条件、极限条件、破坏机构条件的解
二．虚功原理和虚功率原理
虚功原理：在外力作用下处于平衡的变形体，若给物体 一微小的虚变形（位移）。则外力的虚功必等于应力的 虚功（物体内储存的虚应变能）。
V

* f i ui*dV Fi ui*dS s ij ij dV ST V
s ij s ji
j i s ij ij s s ji ij 2 x j x x
s ij ui f i ui dV s ij dV s ij ij dV x x j j V V V
体力为零时：
ST * * F u dS s i i ij ijdV V
结构的塑性极限分析


梁的弹塑性弯曲 塑性极限分析定理和方法 梁的极限分析
§1 梁的弹塑性弯曲
一．基本假定 平截面假设：在变形过程中，变形 前为平面的横截面，变形后仍保持 为平面，且与变形后梁的轴线垂直。 z x P
b h z x l/2 l/2
y

纵向纤维互不挤压：不计挤压应力， 横截面上只有正应力。
* 0 * F u dS s i i ij ijdV V
* ij :
i* : u
体力为零时：
ST
三．塑性极限分析定理
1. 下限定理：
静力允许的内力场：满足平衡条件（平衡微分方程和面力边界 条件），不违背屈服条件的内力场。sPi s : 静力允许载荷系数 [ 放松破坏机构条件（几何方程、位移和速度边界条件）] 真实内力场：满足静力平衡条件、屈服条件、破坏机构条件的 内力场。 真实内力场一定是静力允许的内力场。 塑性极限载荷系数：l = s
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

弹塑性变形与极限载荷分析
14-3 超静定桁架的极限载荷
图示的超静定结构，由刚性梁 BE 与各杆的横截面面积分 A1 A3 A , A2 2 A 。各杆 别为 A1、A2、A3 的杆1、杆2、杆3 组成，且， 的材料相同，其拉、压屈服强度均为 s 。试求该结构的极限载荷。 解：一次超静定结构，有两根 杆屈服才进入塑性极限状态。 故有三种可能的极限状态。 1）设杆1与杆2已屈服，杆 3未屈服。此时，载荷 F 有使 刚性梁绕E点转动的趋势。 ME 0 , MD 0 例
E E ( s ) s
( s ) ( s ) (14 - 5)
E E
弹塑性变形与极限载荷分析
14-2 应力-应变关系曲线的简化 1）理想弹塑性材料
2）理想刚塑性材料 3）线性强化材料 4）幂函数强化材料
s s
弹塑性变形与极限载荷分析
14-1 弹塑性变形与极限载荷法概念 2）极限载荷法 图中所示的一次超静定结构，各杆的横截面相同并均为理想 弹塑性材料，a >b 。设各杆均处于弹形变形状态时，杆1、杆2、 杆 3 的内力分别为 FN 、FN 、FN ，可以分析得到，在外力一定 FN1 FN 2 FN 3 。 时， 当外力增大使杆3屈服时，杆3已失去承载能力。由于杆2和杆1 尚未屈服，它们组成一静定结构，仍可继续承受增加的载荷。
m
(14 - 6)
弹塑性变形与极限载荷分析
14-3 超静定桁架的极限载荷
由对 14-1 节中一次超静定桁架的分析可知，当其中一根杆 （多余约束的杆）屈服时，便变为静定杆件结构。此时增大载荷， 若再有一根杆屈服，结构便处于塑性极限状态。以此类推，对于 n 次超静定桁架，如果有 n+1 根杆屈服，该结构便处于塑性极限 状态。
n次超静定结构的求解，需要n个补充条件。这里再加上欲 求的极限载荷，则共需要 n+1个补充条件。而当n次超静定桁架 处 于 塑 性 极 限 状 态 时 ， 已 屈 服 的 n+1 根 杆 的 内 力 成 为 已 知 （ F N Ai s (i 1,2,3 , n 1) ），这恰好提供了n+1个补充条件。 i 这样，超静定桁架的极限载荷可根据塑性极限状态时平衡条件求 得。
F 3FN1s 2 FN2s 7 A s FN 3 2 FN1s FN2s 4 A s > FN3s
弹塑性变形与极限载荷分析
14-3 超静定桁架的极限载荷
弹塑性变形与极限载荷分析
14-1 弹塑性变形与极限载荷法概念
1）弹塑性变形
以前我们所研究的问题是限制在材料始终保持在线性弹性范围 内，外力、内力、应力、应变、变形与位移各量间不仅成线性关系， 而且还单值对应。对某一构件或结构在一定外力作用下必产生确定 的内力、应力、应变、变形与位移。这就是说，如果外力增大 n 倍， 其对应的内力、应力、应变、变形与位移也增大 n倍。这样，力作 用的最终效果（例如产生的应变与变形等）只决定于力的最终值， 而与力作用的先后次序无关。在对构件或结构进行强度计算时，采 用极限应力法，即对塑性材料制成的构件或结构，当其危险点一点 处相当应力达到材料的屈服强度 s时，便认为整个构件或 或 0.2 结构已处于极限状态而不能继续承受更大的载荷。
Fu
表
F [ Fu ]
式中
[ Fu ]
(14 -1)
(14 - 2)
n 为安全系数 采用式(14-1)来计算构件或结构发生塑性变形时的强度的方 法，称为极限载荷法。
Fu n
弹塑性变形与极限载荷分析
14-2 应力-应变关系曲线的简化 1）理想弹塑性材料
E s
( s ) ( s ) (14 - 3)
弹塑性变形与极限载荷分析
14-1 弹塑性变形与极限载荷法概念
1）弹塑性变形 材料进入塑性状态后，应力与应变之间不仅成非线性关系， 而且不一一对应。力对构件的作用效果不只取决于力的最终值， 而且还与力的作用历史以及作用的先后顺序有关。 以轴向拉压杆为例
先加 F1 后加 F2 先加 F2析
14-2 应力-应变关系曲线的简化 1）理想弹塑性材料
2）理想刚塑性材料
0 s
( p 0) ( p 0) (14 - 4)
p 为塑性应变
弹塑性变形与极限载荷分析
14-2 应力-应变关系曲线的简化 1）理想弹塑性材料
2）理想刚塑性材料 3）线性强化材料
弹塑性变形与极限载荷分析
14-1 弹塑性变形与极限载荷法概念
1）弹塑性变形 事实上，对塑性材料制成的应力非均匀分 布的构件或超静定结构，例如图中所示的简支 梁，当危险截面Ⅰ-Ⅰ上危险点A或B处应力等于 材料的屈服强度 s或 0.2时，便出现塑性变形。 但是，由于Ⅰ-Ⅰ截面上应力线性分布，整个截 面除 A 、 B 两点外，其他各点应力并没有达 到 s或 0，仍处于弹形变性状态。此时，可 .2 继续增大载荷，梁Ⅰ-Ⅰ上会有更多的点进入塑 性变形状态，形成了塑性区域，梁进入了弹塑 性变形状态。
1 2 3
直到杆2也 屈服 ， 该结 构才失去抵 抗变形能力 而成为几何 可变“机构”
弹塑性变形与极限载荷分析
14-1 弹塑性变形与极限载荷法概念 2）极限载荷法
由于塑性变形所形成的几何可变“机构”，称为塑性机构。 使构件或结构变成塑性机构时的载荷称为极限载荷。 与塑性机构相应的状态称为塑性极限状态。 若以塑性极限状态作为构件或结构的危险状态，并用 示极限载荷，那么相应的强度条件应为
14-1 弹塑性变形与极限载荷法概念
1）弹塑性变形 2）极限载荷法 上述分析可知，对塑性材料制成的超静定结构或应力非均匀 分布的构件，当其危险点一点处相当应力达到材料屈服强度时， 整个构件或结构仍能继续承受更大的载荷。这样，极限应力法在
此已无法分析构件或结构发生弹塑性变形后的承载能力，需要研
究新的分析方法。