区间估计公式补充说明

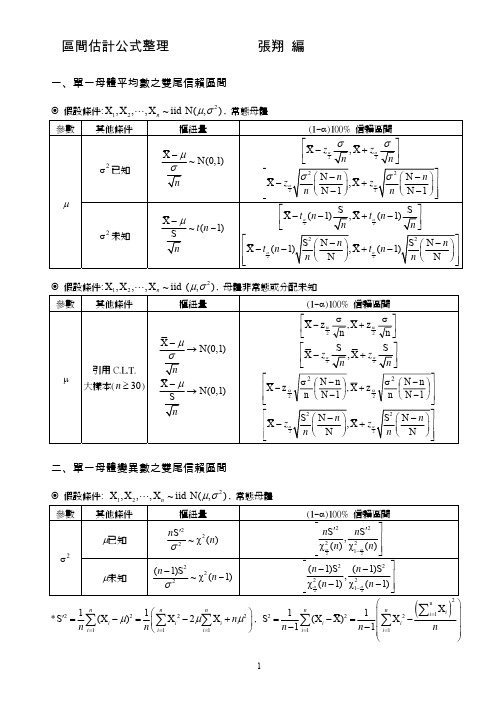
區間估計公式整理 張翔 編一、單一母體平均數之雙尾信賴區間假設條件:2X ,X ,,X ~iid N(,)µσ", 常態母體假設條件:2X ,X ,,X ~iid (,)µσ", 母體非常態或分配未知二、單一母體變異數之雙尾信賴區間假設條件: 2X ,X ,,X ~iid N(,)µσ", 常態母體 *222211111X )X 2X S (µµµ===⎛⎞′=−=−+⎜⎟⎝⎠∑∑∑nnni i i i i i n n n 2n122211X 11S (X X)X 11===⎛⎞⎜⎟=−=−⎜⎟−−⎜⎟⎝⎠∑∑∑n n ii i i i i n n n,三、單一母體比例之雙尾信賴區間假設條件:X ,X ,,X ~iid Ber()p ", 母體Bernoulli 分配 *其中 1Xˆii p n==∑四、兩獨立母體平均數差異之雙尾信賴區間假設條件:21211X ,X ,,X ~iid N(,)n µσ", 21222Y ,Y ,,Y ~iid N(,)n µσ", 常態母體*其中 222112212(1)S (1)S 2pn n S n n −+−=+−221212Welch2222121212S S df S S 11n nn n n n ⎛⎞+⎜⎟⎝⎠=⎛⎞⎛⎞⎜⎟⎜⎟⎝⎠⎝⎠+−−,假設條件: 21211X ,X ,,X ~iid (,)n µσ", 21222Y ,Y ,,Y ~iid (,)n µσ", 母體非常態或分配未知 *若12未知則以代入, 餘皆不變12五、兩相依母體平均數差異之雙尾信賴區間假設條件:2X ,X ,,X ~iid N(,)µσ", 2Y ,Y ,,Y ~iid N(,)µσ", 常態母體 *其中, 故22D11S (D D)1ni i n ==−−∑D X Y i i i =−212D DD ,D ,,D ~iid N(,)n µσ",假設條件: 21211X ,X ,,X ~iid (,)n µσ", 21222Y ,Y ,,Y ~iid (,)n µσ", 母體非常態或分配未知 *其中, 故22D11S (D D)1ni i n ==−−∑D X Y i i i =−212D DD ,D ,,D ~iid (,)n µσ",六、兩獨立母體變異數比例之雙尾信賴區間假設條件:21211X ,X ,,X ~iid N(,)n µσ", 21222Y ,Y ,,Y ~iid N(,)n µσ", 常態母體 *其中12211111X )i i n S (µ=′=−∑22222121(Y i i n ,S )µ=′=−∑1221111X 1i i n ==−−∑S (,X)2222121Y Y)1ii n ==−−∑S ( ,七、兩獨立母體比例差異之雙尾信賴區間假設條件:X ,X ,,X ~iid Ber()p ", Y ,Y ,,Y ~iid Ber()p ", 常態母體 *其中 1111XˆX ii p n ===∑2122YˆY ii pn ===∑,。

(1) P值是：1) 一种概率，一种在原假设为真的前提下出现观察样本以及更极端情况的概率。

2) 拒绝原假设的最小显著性水平。

3) 观察到的(实例的) 显著性水平。

4) 表示对原假设的支持程度，是用于确定是否应该拒绝原假设的另一种方法。

(2) P 值的计算：一般地，用X 表示检验的统计量，当H0 为真时，可由样本数据计算出该统计量的值C ，根据检验统计量X 的具体分布，可求出P 值。

具体地说:左侧检验的P 值为检验统计量X 小于样本统计值C 的概率，即:P = P{ X < C}右侧检验的P 值为检验统计量X 大于样本统计值C 的概率:P = P{ X > C}双侧检验的P 值为检验统计量X 落在样本统计值C 为端点的尾部区域内的概率的2 倍: P = 2P{ X > C} (当C位于分布曲线的右端时) 或P = 2P{ X< C} (当C 位于分布曲线的左端时) 。

若X 服从正态分布和t分布，其分布曲线是关于纵轴对称的，故其P 值可表示为P = P{| X| > C} 。

计算出P 值后，将给定的显著性水平α与P 值比较，就可作出检验的结论:如果α > P 值，则在显著性水平α下拒绝原假设。

如果α ≤ P 值，则在显著性水平α下接受原假设。

在实践中，当α = P 值时，也即统计量的值C 刚好等于临界值，为慎重起见，可增加样本容量，重新进行抽样检验。

整理自：区间估计区间估计（Interval Estimation）[编辑]什么是区间估计区间估计就是以一定的概率保证估计包含总体参数的一个值域，即根据样本指标和抽样平均误差推断总体指标的可能范围。

它包括两部分内容：一是这一可能范围的大小；二是总体指标落在这个可能范围内的概率。

区间估计既说清估计结果的准确程度，又同时表明这个估计结果的可靠程度，所以区间估计是比较科学的。

用样本指标来估计总体指标，要达到100%的准确而没有任何误差，几乎是不可能的，所以在估计总体指标时就必须同时考虑估计误差的大小。

（二）区间估计区间估计是指用样本指标、抽样误差和概率所构造的区间以估计总体指标存在的可能范围。

在进行区间估计的时候，根据所给定的条件不同，总体平均数和总体成数的估计有两条模式可供选择： 第一套：给定置信度要求，去推算抽样误差的可能范围。

第二套：根据已给定的抽样误差范围，求出概率保证程度。

1. 总体平均数的区间估计按照第一套模式，根据置信度F t ()的要求，估计极限抽样误差的可能范围)(∆∆∆或p x ，并指出估计区间（置信区间）。

具体步骤是：（1）抽取样本，并根据调查所得的样本单位标志值，计算样本平均数x ；计算样本标准差；在大样本下用以代替总体标准差推算抽样平均误差μ。

（2）根据给定的置信度F t ()的要求，查《正态分布概率表》，求得概率度t 值。

（3）根据概率度t 和抽样平均误差μx 计算极限抽样误差的可能范围μxx t =∆，并据以计算置信区间的上下限。

例14 麦当劳餐馆在7周内抽查49位顾客的消费额（元）如下，求在概率95%的保证下，顾客平均消费额的置信区间。

15 24 38 26 30 42 1830 25 26 34 44 20 3524 26 34 48 18 28 4619 30 36 42 24 32 4536 21 47 26 28 31 4245 36 24 28 27 32 3647 35 22 24 32 46 26第一步：根据样本计算样本平均数和标准差：x x n ==∑32 （元） S n x x ==-∑2945().（元），用样本标准差代替总体标准差σ=945.（元） 样本平均误差 x n μσ===94549135..（元）第二步：根据给定的置信度F t ()=95%，查概率表得t =196. 第三步：根据概率度t 和抽样平均误差推算抽样极限误差的可能范围。

65.235.196.1=⨯==∆μxx t （元） 将μxx ,的值代入区间估计公式 )(65.34)(35.2965.23265.232元元≤≤+≤≤-+≤≤-∆∆X X x X x xx计算结果表明，以95%的概率保证，麦当劳餐馆顾客消费额在29.35~34.65元之间。

总体参数的区间估计公式在进行区间估计时，我们首先需要收集到一个样本，并根据样本对总体参数进行估计。

然后根据样本的统计量，结合分布的性质和抽样方法，建立置信区间。

设总体参数为θ，我们希望得到它的置信水平为1-α的置信区间。

置信水平表示我们对总体参数的估计的可信程度，一般常用的置信水平有90%、95%和99%等。

参数估计的方法有很多，具体的方法选择取决于总体参数的性质、样本的大小以及其他假设条件。

常见的参数估计方法有：1.总体均值的区间估计：假设总体呈正态分布，样本大小为n，则总体均值的区间估计公式为：[样本均值-Z值（α/2）*总体标准差/√(n),样本均值+Z值（α/2）*总体标准差/√(n)]其中Z值（α/2）为标准正态分布的分位数，可以从标准正态分布表中查得。

2.总体比例的区间估计：假设总体为二项分布，样本大小为n，成功的次数为x，则总体比例的区间估计公式为：[样本比例-Z值（α/2）*√(样本比例*(1-样本比例)/n),样本比例+Z值（α/2）*√(样本比例*(1-样本比例)/n)]其中Z值（α/2）为标准正态分布的分位数，可以从标准正态分布表中查得。

3.总体方差的区间估计：假设总体呈正态分布，样本大小为n，则总体方差的区间估计公式为：[(n-1)*样本方差/卡方分布（α/2）,(n-1)*样本方差/卡方分布（1-α/2])]其中卡方分布是用于描述自由度为n-1的卡方随机变量的概率分布，可以从卡方分布表中查得。

以上是常见的总体参数区间估计公式，这些公式是根据统计学理论推导而来的，适用于不同情况下的参数估计。

在实际应用中，我们根据具体问题和假设条件选择适当的参数估计方法，计算置信水平的区间估计，从而对总体参数进行估计和推断。