最新区间估计与假设检验公式表

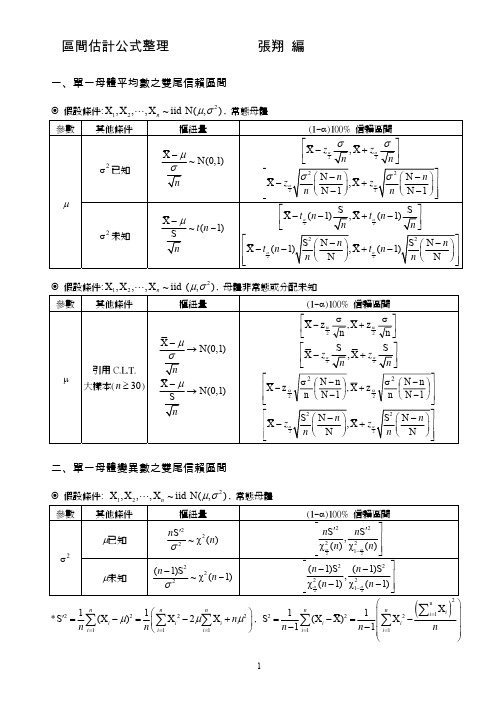
區間估計公式整理 張翔 編一、單一母體平均數之雙尾信賴區間假設條件:2X ,X ,,X ~iid N(,)µσ", 常態母體假設條件:2X ,X ,,X ~iid (,)µσ", 母體非常態或分配未知二、單一母體變異數之雙尾信賴區間假設條件: 2X ,X ,,X ~iid N(,)µσ", 常態母體 *222211111X )X 2X S (µµµ===⎛⎞′=−=−+⎜⎟⎝⎠∑∑∑nnni i i i i i n n n 2n122211X 11S (X X)X 11===⎛⎞⎜⎟=−=−⎜⎟−−⎜⎟⎝⎠∑∑∑n n ii i i i i n n n,三、單一母體比例之雙尾信賴區間假設條件:X ,X ,,X ~iid Ber()p ", 母體Bernoulli 分配 *其中 1Xˆii p n==∑四、兩獨立母體平均數差異之雙尾信賴區間假設條件:21211X ,X ,,X ~iid N(,)n µσ", 21222Y ,Y ,,Y ~iid N(,)n µσ", 常態母體*其中 222112212(1)S (1)S 2pn n S n n −+−=+−221212Welch2222121212S S df S S 11n nn n n n ⎛⎞+⎜⎟⎝⎠=⎛⎞⎛⎞⎜⎟⎜⎟⎝⎠⎝⎠+−−,假設條件: 21211X ,X ,,X ~iid (,)n µσ", 21222Y ,Y ,,Y ~iid (,)n µσ", 母體非常態或分配未知 *若12未知則以代入, 餘皆不變12五、兩相依母體平均數差異之雙尾信賴區間假設條件:2X ,X ,,X ~iid N(,)µσ", 2Y ,Y ,,Y ~iid N(,)µσ", 常態母體 *其中, 故22D11S (D D)1ni i n ==−−∑D X Y i i i =−212D DD ,D ,,D ~iid N(,)n µσ",假設條件: 21211X ,X ,,X ~iid (,)n µσ", 21222Y ,Y ,,Y ~iid (,)n µσ", 母體非常態或分配未知 *其中, 故22D11S (D D)1ni i n ==−−∑D X Y i i i =−212D DD ,D ,,D ~iid (,)n µσ",六、兩獨立母體變異數比例之雙尾信賴區間假設條件:21211X ,X ,,X ~iid N(,)n µσ", 21222Y ,Y ,,Y ~iid N(,)n µσ", 常態母體 *其中12211111X )i i n S (µ=′=−∑22222121(Y i i n ,S )µ=′=−∑1221111X 1i i n ==−−∑S (,X)2222121Y Y)1ii n ==−−∑S ( ,七、兩獨立母體比例差異之雙尾信賴區間假設條件:X ,X ,,X ~iid Ber()p ", Y ,Y ,,Y ~iid Ber()p ", 常態母體 *其中 1111XˆX ii p n ===∑2122YˆY ii pn ===∑,。

实验二、区间估计与假设检验实验（验证性实验）1、实验目的掌握正态总体的均值，方差的区间估计与假设检验以及非参数检验。

2、实验要求及学时：实验形式（个人）；实验学时数4。

3、实验环境及材料（使用的软件系统、实验设备、主要仪器、材料等）。

装有版本为8.1以上的SAS系统的个人电脑（每人一台）。

4、实验内容用SAS软件进行正态总体的均值，方差的区间估计与假设检验以及非参数检验。

5、实验方法和操作步骤1）生成数据data zt;retain _seed_ 0;mu1=0;mu2=2;sigma1=1;sigma2=4;do _i_=1to1000;normal1=mu1+sigma1*rannor(_seed_);normal2=mu2+sigma2*rannor(_seed_);output;end;drop _seed_ _i_ mu1 sigma1 mu2 sigma2;run;这个步骤用rannor函数生成两个正态分布的变量保存在数据表zt中。

2）运用univariate过程作正态性检验。

proc univariate data=zt normal;var normal1 normal2;histogram normal1 normal2;probplot normal1 normal2;/*正态性假设检验*/run;这步的结果如下：表2-1：normal1的正态性检验结果图2-1：normal1的直方图图2-2：normal1的QQ图分析: 表2-1中的p-value都是大于0.05的,从检验的数量结果显示变量normal1是服从正态分布的,从直方图和QQ图我们也可以看到,直方图是对称的，而QQ图也是一条直线。

在程序的结果中还会相应的给出normal2的检验结果。

3）用ttest过程对变量normal1均值假设检验（0:0Hμ=）。

proc ttest data=zt h0=0alpha=0.01;/*总体均值的假设检验*/ var normal1;run;这步的结果如下：表2-2：normal1均值的假设检验分析: 表2-2中的p-value等于0.5312，远大于0.05的,从检验的数量结果显示变量normal1μ=是被接受的。

常见假设检验公式的详细解析假设检验是统计学中常用的一种推断方法，用于判断一个假设是否成立。

常见的假设检验公式有很多种，下面将对其中几种进行详细解析。

1. 单样本均值检验公式假设我们有一组观测值X₁，X₂，...，Xₙ，要检验这些观测值的总体均值是否等于某个值μ₀。

假设检验的原假设（H₀）是：总体均值等于μ₀，备择假设（H₁）是：总体均值不等于μ₀。

使用t检验进行检验时，计算统计量的公式如下：t = (x - μ₀) / (s/√n)其中，x是样本均值，s 是样本标准差，n 是样本容量。

根据t值和自由度的对应表，可以得到该t值的显著性水平和p值。

2. 双样本均值检验公式双样本均值检验用于比较两组样本的均值是否有显著差异。

假设我们有两组样本X₁，X₂，...，Xₙ和Y₁，Y₂，...，Yₙ，要检验它们的总体均值是否相等。

使用独立样本t检验进行检验时，计算统计量的公式如下：t = (x₁ - x₂) / √((s₁²/n₁) + (s₂²/n₂))其中，x₁和x₂分别是两组样本的均值，s₁和 s₂分别是两组样本的标准差，n₁和 n₂分别是两组样本的容量。

根据t值和自由度的对应表，可以得到该t值的显著性水平和p值。

3. 单样本比例检验公式单样本比例检验用于检验样本的比例是否等于某个给定的比例。

假设我们有一组观测值，成功的事件发生的次数为x，总事件发生的次数为n，要检验成功的概率是否等于某个给定的比例p₀。

使用正态分布的近似方法进行检验时，计算统计量的公式如下：z = (p - p₀) / √(p₀(1-p₀)/n)其中，p是样本成功的比例，p₀是给定的比例，n 是样本容量。

根据z值和显著性水平的对应关系，可以得到该z值的p值。

总结：上述所介绍的是常见假设检验公式中的几种，每种假设检验有其适用的前提条件和计算公式。

在进行假设检验时，需要注意选择适当的公式和假设检验方法，以及正确计算统计量并进行显著性检验。