股利贴现模型
- 格式:docx
- 大小:37.89 KB
- 文档页数:3

收益定价模型
收益定价模型(Earnings Pricing Model)是一种用于确定股票
或其他金融资产价格的模型。
该模型尝试通过分析公司的盈利能力来估计资产的合理价格。
常见的收益定价模型有以下几种:
1. 资本资产定价模型(Capital Asset Pricing Model,CAPM):基于风险和预期回报之间的线性关系,通过考虑资产相对于市场的风险来确定合理的期望收益率,并进而确定资产价格。
2. 股利贴现模型(Dividend Discount Model,DDM):基于公
司未来的股利或现金流量来确定股票的合理价格。
该模型将未来收益现值化,然后将其与当前股票价格进行比较。
3. 增长定价模型(Growth Pricing Model):适用于快速增长
的公司,该模型基于预计未来增长率来确定股票的合理价格。
通常使用过去的增长数据和预测的未来增长来估计。
4. 相对估值模型(Relative Valuation Model):将公司或资产
与类似公司或资产进行比较,通过比较相似公司的估值指标(如市盈率、市净率等)来确定合理的价格。
该模型基于市场上其他类似公司的估值水平。
这些模型都有其各自的局限性和假设,投资者在使用时需要结合具体情况进行综合分析。
同时,还需要注意到市场上价格由
多种因素影响,例如市场情绪、供需关系等,因此通过单一模型得出的价格可能并不一定准确。

股利贴现模型范文股利贴现模型其中V为每股股票的内在价值,Dt是第t年每股股票股利的期望值,k是股票的期望收益率或贴现率(discount rate)。
公式表明,股票的内在价值是其逐年期望股利的现值之和。
根据一些特别的股利发放方式,DDM模型还有以下几种简化了的公式:?零增长模型?即股利增长率为0,未来各期股利按固定数额发放。
计算公式为:V=D0/k其中V为公司价值,D0为当期股利,K为投资者要求的投资回报率,或资本成本。
零增长模型即股利增长率为0,未来各期股利按固定数额发放。
计算公式为:V=D0/k其中V为公司价值,D0为当期股利,K为投资者要求的投资回报率,或资本成本。
不变增长模型即股利按照固定的增长率g增长。
计算公式为:V=D1/(k-g)注意此处的D1=D0(1+g)为下一期的股利,而非当期股利。
二段、三段、多段增长模型二段增长模型假设在时间l内红利按照g1增长率增长,l外按照g2增长。
三段增长模型也是类似,不过多假设一个时间点l2,增加一个增长率g3优先股:一、优先股通常预先定明股息收益率。
由于优先股股息率事先固定,所以优先股的股息一般不会根据公司经营情况而增减,而且一般也不能参与公司的分红,但优先股可以先于普通股获得股息,对公司来说,由于股息固定,它不影响公司的利润分配。
二、优先股的权利范围小。
优先股股东一般没有选举权和被选举权,对股份公司的重大经营无投票权,但在某些情况下可以享有投票权。
三、如果公司股东大会需要讨论与优先股有关的索偿权,即优先股的索偿权先于普通股,而次于债权人。
第三年现金流较复杂,包括股利和类似优先股的最终价值。
(2)假定股票价格为26元,计算股票的预期收益率。
利用插值法插值法又称“内插法”,是利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数f (x)的近似值,这种方法称为插值法。
因为26 > 25.1,所以贴现率一定小于第一问中的10%,试着用8%算,最终用插值法算出9.68%解决方案1:一年股利=2*(1+8%)=2.098)=(10%-9%)/,股票价值=2.942;(26-25.098当要求的报酬率是9%时.333/.16/.333第三年股利=2.098(2)股票价格26元.16第二年股利=2.16*(1+8%)=2,(i-10%)/,股票价值是25.333/.098-27;(25.942);(1+9%)^2+2.566/(1+9%)+2,当要求的报酬率是10%时.566……(1)股票价值=2.16/.3328*(1+10%)=2;[10%*(1+10%)^2]=25.566第四年股利=2,i=9;[9%*(1+9%)^2]=27;(1+10%)+2;(1+10%)^2+2,运用差值法.68%股票预期收益率是9.566/股利贴现模型股利贴现模型其中V为每股股票的内在价值,Dt是第t年每股股票股利的期望值,k是股票的期望收益率或贴现率(discount rate)。


第一部分收益法模型及方法介绍收益法目前常用的估值模型主要为现金流折现模型(DCF)、股利贴现模型(DDM)。
(一)现金流折现模型(Discounted Cash Flow),简称DCF 模型。
现金流量折现法通常包括FCFF(企业自由现金流折现模型)和FCFE(股权自由现金流折现模型)。
1、FCFF模型(Free Cash Flow for the Firm)(1)公式企业自由现金流量=净利润+税后利息支出+折旧及摊销-资本性支出-营运资金增加额注意:企业整体价值=经营性资产价值+溢余资产价值+非经营性资产负债价值企业股东全部权益价值=企业整体价值-付息债务价值(2)折现率折现率(加权平均资本成本,WACC)计算公式如下:WACC=[E/(E+D)]Re+[D/(E+D)]×(1-T)Rd其中:Re:权益资本报酬率;Rd:债务资本收益率;E:权益的市场价值;D:付息债务的市场价值;T:所得税率。
注:系统性风险(不可分散风险)——不可分散,存在于市场或者行业,每个企业、资产自身都具有的风险。
非系统性风险(可分散风险)——可分散,是某一企业或行业特有的风险,其他行业没有或行业内其他企业没有。
1)Re股权收益率采用资本资产定价模型(CAPM)(Capital Asset Pricing Model)计算。
计算公式如下:Re=Rf+β×ERP+RsRf:无风险收益率一般以国债收益率作为无风险收益率,选择国债剩余年限与标的资产经营年限(预测期限)匹配。
10年期及以上,4%左右。
β:(Unlevered Beta)剔除财务杠杆的行业Beta,可选取沪深300、上证综指、深成指同行业Beta值。
(注意与ERP所采用的的市场指数相互匹配)ERP:市场风险溢价(市场风险超额回报率),系股票市场回报率与无风险报酬率的差额。
《中国资产评估》(2015年1期)中企华,2012-2014年选取200个样本,涉及47家评估机构。

股票估值的股利贴现模型用于实践的难点—、每股股利值的确认在股利贴现模型中,我们希望确定一个能够永续获得的股利额度,然后以此为基础进行折现汇总计算。
然而,在实际投资活动中,这个永续获得的股利额度似乎是很难实现的,主要原因在于以下几个方面。
第一,企业的股利政策并不会一成不变,且随着企业所处发展阶段的不同,企业的股利也会发现变化。
比如,企业处于成长期,可能支付的股利并不会太多,因为企业需要更多的现金以实现快速发展。
另一方面,当企业进入成熟期后,企业的股利支付能力会比成长期增强很多,但若进入衰退期,则很难再保证之前的股利支付。
因此,想要有一个稳定的、持续的股利额度,本身就是一件很困难的事情。
第二,事实上,在A股市场上,能够做到以某种额度稳定分红的企业,本来就是凤毛麟角。
因而,投资者按照股利贴现法计算股票的内在价值,意义也就不太大了。
第三,目前,由于政府一直提倡上市公司要尽可能多地用现金分红的方式回馈投资者,因而越来越多的绩优企业会选择大比例现金分红。
回顾A股市场,长期坚持现金分红的企业还是有一些的,如银行业中的工商银行、家电行业中的格力电器,还有万科A、贵州茅台等,一直以来都有相对稳定的分红。
鉴于企业分红额度具有很大的波动性,因而,采用股利贴现模型中的两阶段模型或多阶段模型是一个不错的选择。
二.折现率的确认折现率是另一个影响整个企业估值计算的核心因素。
同时,由于折现涉及的时间跨度较大,因而,这种折现往往需要反映更多的变数与因素。
第一,累加法。
该方法认为,未来资金的折现应该能够反映无风险利润率、风险收益率以及通货膨胀率等几方面因素。
大多数情况下,我们通常用国债收益率作为无风险收益率的基准数据。
通货膨胀率可能会随着经济形势的变化而调整。
风险收益率则要体现经营风险、行业风险以及财务风险等诸多要素。
第二,市场比较法。
该方法是通过寻找拟评估对象相同或相似规模、行业的资产评估案例,并研究其折现率,进而设定评估对象的折现率。

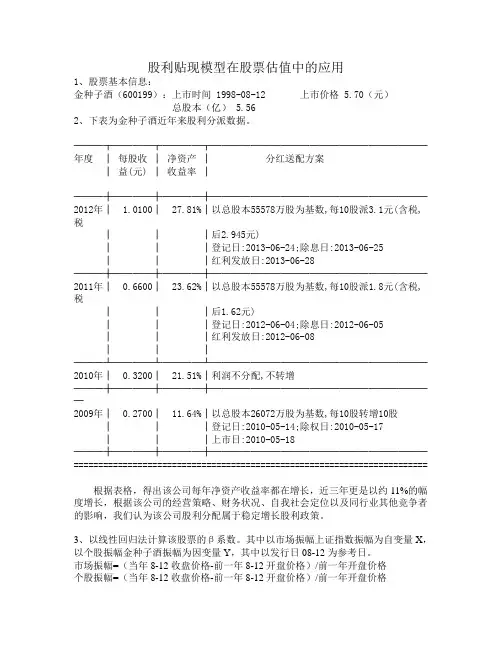
股利贴现模型在股票估值中的应用1、股票基本信息:金种子酒(600199):上市时间 1998-08-12 上市价格 5.70(元)总股本(亿) 5.562、下表为金种子酒近年来股利分派数据。
───┬────┬────┬──────────────────────年度│每股收│净资产│分红送配方案│益(元) │收益率│───┼────┼────┼──────────────────────2012年│ 1.0100│ 27.81%│以总股本55578万股为基数,每10股派3.1元(含税,税│││后2.945元) │││登记日:2013-06-24;除息日:2013-06-25 │││红利发放日:2013-06-28 ───┼────┼────┼──────────────────────2011年│ 0.6600│ 23.62%│以总股本55578万股为基数,每10股派1.8元(含税,税│││后1.62元) │││登记日:2012-06-04;除息日:2012-06-05 │││红利发放日:2012-06-08 │││───┴────┴────┴──────────────────────2010年│ 0.3200│ 21.51%│利润不分配,不转增───┼────┼────┼───────────────────────2009年│ 0.2700│ 11.64%│以总股本26072万股为基数,每10股转增10股│││登记日:2010-05-14;除权日:2010-05-17 │││上市日:2010-05-18 ───┼────┼────┼──────────────────────========================================================================根据表格,得出该公司每年净资产收益率都在增长,近三年更是以约11%的幅度增长,根据该公司的经营策略、财务状况、自我社会定位以及同行业其他竞争者的影响,我们认为该公司股利分配属于稳定增长股利政策。

股利贴现模型、自由现金流量贴现模型及剩余收益模型对股票价格与价值不同解释力的比较分析——来自中国证券市场的实证数据摘要:本文通过对中国证券市场的实证数据进行分析,探讨了股利贴现模型、自由现金流量贴现模型及剩余收益模型对股票价格与价值的解释力。
研究发现,在中国证券市场的实证数据中,自由现金流量贴现模型和剩余收益模型的表现相对较好,而股利贴现模型的解释力相对较弱。
一、引言股票是投资者参与股票市场的一种重要工具,股票市场的价格波动直接影响着投资者的投资决策和预期收益。
因此,研究股票价格与价值的关系,对于投资者进行合理的股票投资具有重要意义。
股利贴现模型、自由现金流量贴现模型及剩余收益模型是目前应用较为广泛的股票估值模型。
二、股利贴现模型股利贴现模型是最早被提出并应用的股票估值模型之一,其核心思想是根据公司未来的股利和股息来衡量股票的价值。
该模型认为,股票的价值应该等于未来的股利折现到现值的总和。
然而,该模型忽视了公司的成长性和未来现金流的变化,对于那些表现出较快成长和高现金流的公司来说,其解释力较弱。
三、自由现金流量贴现模型自由现金流量贴现模型是在股利贴现模型的基础上引入了自由现金流量的概念,具体计算公式为:自由现金流量=净利润+折旧与摊销-资本支出-变动资本。
该模型将公司的自由现金流量折现到现值,并作为衡量股票价值的指标。
在中国证券市场的实证数据中,自由现金流量贴现模型相对于股利贴现模型在预测股票价格和价值方面表现更为准确。
四、剩余收益模型剩余收益模型认为,公司的股票价值等于其未来的净利润和股东权益之间的差额,即剩余收益。
该模型将剩余收益折现到现值,并作为衡量股票价值的指标。
在中国证券市场的实证数据中,剩余收益模型具有较好的解释力,能够对不同类型的公司进行准确的估值。
五、比较与总结综上所述,在中国证券市场的实证数据中,股利贴现模型、自由现金流量贴现模型及剩余收益模型对股票价格与价值的解释力不同。
股利贴现模型由于忽视了公司的成长性和未来现金流的变化,解释力相对较弱。

第一部分收益法模型及方法介绍收益法目前常用的估值模型主要为现金流折现模型(DCF)、股利贴现模型(DDM)。
(一)现金流折现模型(DiscountedCashFlow),简称DCF模型。
现金流量折现法通常包括FCFF(企业自由现金流折现模型)和FCFE(股权自由现金流折现模型)。
1、FCFF模型(FreeCashFlowfortheFirm)(1)公式企业自由现金流量=净利润+税后利息支出+折旧及摊销-资本性支出-营运资金增加额注意:企业整体价值=经营性资产价值+溢余资产价值+非经营性资产负债价值企业股东全部权益价值=企业整体价值-付息债务价值(2)折现率折现率(加权平均资本成本,WACC)计算公式如下:WACC=[E/(E+D)]Re+[D/(E+D)]X(1—T)Rd其中:Re:权益资本报酬率;Rd:债务资本收益率;E:权益的市场价值;D:付息债务的市场价值;T:所得税率。
注:系统性风险(不可分散风险)——不可分散,存在于市场或者行业,每个企业、资产自身都具有的风险。
非系统性风险(可分散风险)——可分散,是某一企业或行业特有的风险,其他行业没有或行业内其他企业没有。
1)Re股权收益率采用资本资产定价模型(CAPM)(CapitalAssetPricingModel)计算。
计算公式如下:Re=Rf+BX ERP+RsRf:无风险收益率一般以国债收益率作为无风险收益率,选择国债剩余年限与标的资产经营年限(预测期限)匹配。
10年期及以上,4%左右。
B:(UnleveredBeta)剔除财务杠杆的行业Beta,可选取沪深300、上证综指、深成指同行业Beta值。
(注意与ERP所采用的的市场指数相互匹配)ERP:市场风险溢价(市场风险超额回报率),系股票市场回报率与无风险报酬率的差额。
《中国资产评估》(2015年1期)中企华,2012-2014年选取200个样本,涉及47家评估机构。
市场风险溢价(ERP)确定方式统计情况如表:每种方法各有利弊,暂无相对完美的方法。


用DDM模型来判断市场理论上的合理市盈率说明:该模型对价值投资应该来说没有太大的用处,但了解一下还是有好处的,如果分析师、投资者太依赖该模型,这样可能会给我们很好的机会,在他们犯错误时,我们就能把握机会。
DDM模型介绍DDM模型(dividend discount model),为股利贴现模型。
是计算公司价值的一种方法,是一种绝对估值方法。
DDM是将公司未来发放的全部股利折现为现值来衡量当前股票价格贵贱的估值模型。
其公式为:股票价值=每股股利÷(折现率-股利增长率)。
在实际使用中,由于中国上市公司分红的“觉悟”不高,因此对公司未来发放股利的预测难度很大;另外是对公式中的折现率的选择也较难确定,且这些变量的任何微小变动都会导致最后得数的大幅波动。
不过,对于那些股利发放策稳定的收益型行业公司或防守型行业公司,DDM可以成为主要的估值标准。
用DDM模型来判断市场理论上的合理市盈率V代表普通股的内在价值,Dt为普通股第t期支付的股息或红利,r为贴现率,t为周期,一般指年份。
通常情况下随着时点的不同贴现率是不断变化的,因此更精确的计算时,r为不同贴现率。
对股息增长率的不同假定,股息贴现模型可以分为:零增长模型、不变增长模型(高顿增长模型)、二阶段股利增长模型(H模型)、三阶段股利增长模型和多元增长模型等形式。
1.零增长模型(Gordon增长模型,即股利增长率为0,未来各期股利按固定数额发放)计算公式为V = D0/K其中V为公司价值,D0为当期股利,K为投资者要求的投资回报率,或资本成本。
2.不变增长模型(即股利按照固定的增长率g增长)计算公式为V = D1/(K—g)注意此处的D1为下一期的股利,而非当期股利3.二段增长模型、三段增长模型、多段增长模型二段增长模型假设在时间l内红利按照g1增长率增长,l外按照g2增长。
三段增长模型也是类似,不过多假设一个时间点l2,增加一个增长率g3DDM模型的适用及不适用适用:分红多且稳定的公司,非周期性行业不适用:分红很少或者不稳定公司,周期性行业;大陆股市的行业结构及上市公司分红比例不高,分红的比例与数量不具有稳定性,难以对股利增长率做出预测,所以对大陆股市基本不适用。
28
2.股利稳定增长时的股利贴现模型
假设公司的每股收益每年都按一定比率 g 递增。
每股收益增长 时的股票价格为Pg,这样就有:
. E + p = --------------------------- 1 ---------------------- E (1 + 0 (1 + i)2
1.无股利增长时的股利贴现模型
设:P ――现在购入股票的价格; n ――持有股票的期限,以年表示; E i 、E 2、…E n ――未来各期公司分配的每股收益;
- n 年后卖出股票的价格;
P n i ――市场利率(即贴现率,或称内在收益率)且大于零。
根据现值公式,现在购买股票的价格就是未来各期的每股收益和第 年
卖出股票时价格的现值,即有:
E1 , Es
P = —-—1 --------- — (l+i)十(1+i 尸 +島+為
E E P = ----------- ] ----------- … ---------------- h Cl + i) (1+0" (1 + i? (1 + __ ]+亠 p = M i L (1 + i 尸」(1 + i 尸 i
P n E* »
27 1-g Pn
(IW
28
如果g > i ,即每股收益的年增长率高于市场利率时 ,因此当n 为无穷大时,[(1+g”(1+i)] 票的价格也会趋于无穷大。
如果g V i ,即每股收益的年增长率低于市场利率,且当
n 为无穷大时 ,就有: P g = E / (i -g)
,(i+g)/(i+i) > 1
n 也会趋于无穷大,这样股。
DDM, CAPM, ATP 三种定价模型(理论)的定义与比较 DDM股利贴现模型(DDM )是贴现现金流估价法评估股权资本价值的一个特例。
这种方法认为,股票的价值是预期未来全部宏利达额现值总和。
其基础是现值分析的应用。
任何资产的价值等于其预期的未来全部现金流的现值总和,计算限制的贴现率应与现金流的风险相匹配。
红利贴现模型的一般形式如公式1。
∑∞=+=1)1(t t t r D V 公式1其中V 为股票内在价值,D t 是第t 年每股股票股利的期望值,r 为市场对该股票收益率的估计。
股利贴现模型说明了股票价格最终决定于持有者们不断增加的现金流收入,即股利。
所以股票售出时对未来红利的预测将决定资本利得。
这一公式默认的条件是投资者长期持有该股,因为绝大多数投资者并非在投资之后永久性地持有所投资的股票,根据收入资本化法,卖出股票的现金流收入也应该纳入股票内在价值的计算。
公式2∑∞=++=1)1(t t n t n r D V 公式2CAPM资本资产定价模型(CAPM )是现代金融市场价格理论的支柱,主要研究证券市场中资产的预期收益率与风险资产之间的关系。
理论的主要前提是资本运作的市场是完全有效的,投资者都是理智的。
理论可以概括为:))(()(f m im f i R R E R R E -+=β公式3其中E(R i )是资产的预期收益率,R f 是无风险收益率,βim 是β系数,E(R m )是市场的预期收益率,(E(R m ) - R f )是市场溢价。
之所以有市场溢价是因为根据马科威茨的理论,风险越高的投资收益也相应越高,投资者承担了与证券市场相关的不可分散风险而预期得到的回报。
而β系数则表示了资产的回报率对市场变动的敏感度,可以衡量该资产的不可分散风险。
如果投资者投入了市场上所有的股票,那么β就等于1。
一般投资的股票越多,越分散则β值越接近1。
APT套利定价模型(ART )其实是基于CAPM 模型的,也可以说是CAPM 的一个扩展理论,该模型同样也是解释资本资产的预计收益率,但它的理论基础是收益率是各种因素综合作用的结果,而不是只考虑投资组合内部不可分散风险。
.股利贴现模型若假定股利是投资者在正常条件下投资股票所直接获得的唯一现金流,则可以建立股价模型对普通股进行估值,这就是着名的股利贴现模型(dividend discount model,DDM )其一般形式为:其中,D 代表普通股的内在价值代表普通股第t 期支付的股息或红利r 是贴现率,又称资本化率。
例题1:A 公司生产的产品在产品生命周期中是成熟的产品。
该公司预计第1年支付股息1元,第2年支付股息0.9元,第3年支付股息0.85元,合理的股票收益率是7%求该公司的股票价值。
解:根据股利贴现模型有 公司的股票价值为)(42.2%)71(85.0%)71(9.0%711)1()1(13233221元=+++++=+++++=r D r D r D D 1、零增长模型(zero-growth model )假定:红利固定不变,即红利增长率为零。
当: R >0 , 上式可以简化表达为:其中,D 代表普通股的内在价值代表普通股第t 期支付的股息或红利代表初期支付的股利r 是贴现率例题2:股票A 将在未来每年都发放2元红利,分析师估计该股票的理论收益率为8%,该股票现在的价值是多少?解:根据股利贴现模型有 公司的股票价值为)(25%82)1(01元==≈+=∑∞=rD r D D t tt 2、不变增长模型又称Gordon 模型假定:股利增长速度为常数,即g D D D g t t t t =-=--11 根据Gordon 模型前提条件,贴现率大于股利增长率,即r>g,则gr D g r g D D -=-+=101其中, 为第1期支付的股利例题3:股票G 预计明年将发放股利2.0元,并且以后将每年增加4%的股利,假设无风险资产的收益率6%,市场组合的平均收益率10%,该股票的贝塔系数为1.5。
根据CAPM 模型和不变增长模型估算该股票的合理投资价值? 解:根据CAPM 模型得. 股票要求的收益率为根据股利贴现模型得 公司的股票价值为)(25%4%1221元=-=-=g r D D 例题4:假定某普通股,面值1元,基年盈利0.50元/股,盈利成长率为5%,股利支付率85%,折现率为10%则其评估价值是多少?如果该股票当前的市场价格为10元,问该公司股票是被高估还是被低估?解:根据股利贴现模型得公司的股票价值为)(93.8%5%10%)51(50.0%8510元=-+⨯=-+=g r g D D 如果该股票当前的市场价格为10元,高于股票的内在价值8.93元,说明该公司的股票被高估了。
可变增长股利贴现模型内在价值的计算公式好的,以下是为您生成的文章:在谈论可变增长股利贴现模型内在价值的计算公式之前,我先跟您唠唠我曾经遇到的一件有意思的事儿。
那是几年前,我参加了一个投资理财的交流活动。
现场有个年轻人,雄心勃勃地想要在股市里大展拳脚。
他激情满满地跟周围人分享着自己的“宏伟计划”,说要靠炒股赚大钱,实现财务自由。
然而,当别人问他一些基本的财务知识,比如股利贴现模型,他却一脸茫然。
这让我深刻地意识到,理论知识对于实际投资操作是多么的重要。
咱们言归正传,来聊聊可变增长股利贴现模型内在价值的计算公式。
这个公式啊,就像是一个神秘的魔法咒语,能帮我们揭开股票内在价值的面纱。
它的基本形式是:股票的内在价值等于未来各期股利的现值之和。
假设一家公司在初始阶段的股利增长率较低,比如说第一年股利为D1 ,增长率为 g1 ,持续 n1 年;然后进入一个高速增长阶段,增长率变为 g2 ,持续 n2 年;最后进入稳定增长阶段,增长率为 g3 ,一直持续下去。
那么,这股票的内在价值 V 就可以这样计算:首先计算初始阶段股利的现值:P1 = D1 / (1 + r) ^ 1 + D1 × (1 + g1) / (1 + r) ^ 2 +... + D1 × (1 + g1) ^ (n1 - 1) / (1 + r) ^ n1接着计算高速增长阶段股利的现值:P2 = D1 × (1 + g1) ^ n1 × (1 + g2) / [(1 + r) ^ n1 × (r - g2)] × [1 - ((1 +g2) / (1 + r)) ^ n2]最后计算稳定增长阶段股利的现值:P3 = [D1 × (1 + g1) ^ n1 × (1 + g2) ^ n2 × (1 + g3) / (r - g3)] / (1 + r) ^ (n1 + n2)将 P1、P2、P3 相加,就得到了股票的内在价值 V 。
股利贴现模型
若假定股利是投资者在正常条件下投资股票所直接获得的唯一现金流,则可以建立股价模型对普通股进行估值,这就是著名的股利贴现模型(dividend discount model,DDM )其一般形式为:
D1D2 D 3D t D t
D
(1 r )2(1 r) 3(1 r )t t 1 (1 r )t
1 r
其中, D 代表普通股的内在价值
代表普通股第t 期支付的股息或红利
r是贴现率,又称资本化率。
例题 1: A 公司生产的产品在产品生命周期中是成熟的产品。
该公司预计第
元,第 2 年支付股息0.9 元,第 3 年支付股息0.85 元,合理的股票收益率是股票价值。
解:根据股利贴现模型有1 年支付股息1 7%求该公司的
D
D1D2D3 1r(1 r )2(1 r )3
公司的股票价值为
10.90.85
17%(17%)2(17%) 3
2.42(元)
1、零增长模型(zero-growth model )
假定:红利固定不变,即红利增长率为零。
D t
D01
D
(1 r )t
t 1 (1 r )t t 1
当:R >0 ,上式可以简化表达为:
D D
0 r
其中, D 代表普通股的内在价值
代表普通股第t 期支付的股息或红利
代表初期支付的股利
r是贴现率
例题 2:股票 A 将在未来每年都发放 2 元红利,分析师估计该股票的理论收益率为8%,该股票现在的价值是多少?
解:根据股利贴现模型有
D t
D
t 1 (1r ) t
公司的股票价值为D
r
2
25(元) 8%
2、不变增长模型
又称 Gordon 模型
假定:股利增长速度为常数,即g t D t D t 1
g D t1
根据 Gordon 模型前提条件,贴现率大于股利增长率,即 r>g, 则D D01g D
1 其
r g r g 中,为第 1 期支付的股利
例题 3:
股票 G 预计明年将发放股利 2.0 元,并且以后将每年增加4%的股利,假设无风险资产的收
益率 6%,市场组合的平均收益率10%,该股票的贝塔系数为 1.5。
根据 CAPM 模型和不变增长模型估算该股票的合理投资价值?
解:根据 CAPM 模型得
股票要求的收益率为
r6% 1.5(10%6%)12%
根据股利贴现模型得
公司的股票价值为D D1225(元)
r g12%4%
例题 4:
假定某普通股,面值 1 元,基年盈利0.50 元 /股,盈利成长率为5%,股利支付率85%,折现率为10%则其评估价值是多少?如果该股票当前的市场价格为10 元,问该公司股票是
被高估还是被低估?解:根据股利贴现模型得
D D01g
公司的股票价值为
r g
85%0.50(15%)
8.93(元 )
10%5%
如果该股票当前的市场价格为10 元,高于股票的内在价值8.93 元,说明该公司的股票
被高估了。
理性的投资者为了避免股票价格下跌,可能卖出他所持有的股票。
H模型
为了最大限度保留对股票内在价值的计算能力、简化计算过程,得出三阶段股利增长模型
的简化版—— H 模型。
D0 (1 g b ) D0H ( g a g b )
其一般形式: D
r g b
r g b
例题 5:公司现期每股派发股利 2 元。
目前的增长率是20%,分析师预计在未来 10年中将会线性回落至5%的稳定增长。
对股权的必要收益率为12%。
计算每股价值。
解:根据
股利贴现 H 模型有
H=5( 年 )
D 0 (1 g b ) D0 H ( g a g b ) D r g
b r g b
公司的股票价值为2(15%)25(20% 5%) 12%5%12%5% 51.43(元 )
4、多元增长模型( multiple-growth model)
多元增长模型假定在某一时点T 之前红利增长率不确定,但在T 期之后红利增长
T D
t D T1
率为一常数 g,估值模型公式表达为:D
t 1 (1 r )t(1 r )T (r g )
例题 6:A 公司生产的产品在产品生命周期中是成熟的产品。
该公司预计第 1 年支付股息 1 元,第 2 年支付股息0.9 元,第3 年支付股息0.85 元。
第 3 年后,股息预计每年下降3%。
合理的股票收益率是7%。
求该公司的股票价值。
解:根据股利贴现模型有
T D t D
T 1
D t 1 (1 r )t(1 r )T (r g )
公司的股票价值为
10.90.850.85(13%)
17%(17%) 2(17%) 3(17%)3 (7%3%)
9.14(元)
1、公司自由现金流模型
公司自由现金流( FCFF,Free Cash Flow of Firm )是公司支付了所有营运费用、进行
了必需的固定资产与营运资产投资后可以向所有投资者分派的税后现金流量。
FCFF=EBIT ×( 1-税率) +折旧 -资本性支出 -追加营运资本
n
FCFF t V
e K e
V
d K d (1 t)
公司价值: V t WACC
t 1(1 WACC )V V
债务成本=借款利率(1-所得税税率)
股权成本: CAPM 模型
例题 7: C 公司的资本60%来自于股票发行,股东对公司股票的收益率要求为12%,其余通过发行债券筹的,利率为 10%,公司所得税率为 25%,问公司的加权平均资本成本为多少?解:根据题意得
公司的加权平均资本成本为:
WACC = 60% × 12% +( 1-60% )× 10%×( 1-25% )
= 10.2 %。