第11章 股利贴现模型(德意志银行Excel金融工程建模)
- 格式:xls
- 大小:44.00 KB
- 文档页数:1



2021~2022CFA二级笔记11-equity-股利贴现模型CFA二级笔记11-equity-股利贴现模型股利贴现模型本章框架一、framework of model(一)DCF model(二)basic concepts of DDM拓展:拓展:什么是股票高送转方案(三)estimation of infinite stream【错题2】反思:没有看清楚题目和材料【错题3】反思:用错公式(一直在死磕g=ROE*b)...二、gordon growth model(一)basic concepts of GGM【错题13】反思:看看上面的笔记...答案是B【错题5】反思:好像这节课没有涉及到total return的概念,但又似曾相识的样子,忘记在哪了。
根据题目,如果新政府落在加拿大,并且分析师认为公司ABC 是公允定价的,也就是内在价值等于市场价格,下面哪个说法是正确的?如果fairly valued,那么公司的total returnrate=discount rate or required rate ,为7.35%,再看材料最后一句话,公司每年以3.5%稳定增长,意味着价格也是. total return=价格增长(capital return)+股利增长(dividend yield)所以,dividend=7.35%-3.5%=3.85%【错题6】反思:没有读懂材料的意思诶所以我把重点用明亮的黄色标记出来了大意就是:公司因为重组原因,未来三年都不会发股利,但是分析师团队认为在第四年会有1.72每股的股利我一开始以为是虽然公司不发股利,但分析师团队就不要你觉得,我要我觉得,未来四年都会发股利,所以.....实际是只有第四年才发,前面三年都是0股利(二)application of GGM【错题1】反思:对implied growth rate 公式不熟悉【错题12】反思:看错题目...题目问的是beyond four years 的implied growth rate,我看漏了beyond....【错题7】反思:我到底为什么做错百思不得其解....估计昨晚边直播边做题,脑子有点转不过来叭....三、multi-stage DDM【错题8】反思:没有get到重点,直接一股脑在死掐H-model怎么画出来,然后怎么算出来.....其实这道题不用算,看材料,Hmodel 的增长率比两阶段模型增长率来得小,那么直接导致估值小啦.答案是A 【错题4】【错题11】反思:用错折现率........【错题10】反思:时间轴画错了……没认真画...多算了一个时间的价值【错题9】反思:画错时间轴了..起点是2017年而不是2018年。


估值理论:股利贴现模型难得今天有半天的空闲时间,简单介绍一下股利贴现模型(DDM)。
别看这个理论的名称有股利两个字,它并不仅仅适用于上市公司股票估值,对于非上市企业估值也能用得上。
本来是不打算写股利贴现模型的,但是在用贴现现金流法做估值的时候,会涉及到终值的计算。
在终值的计算方法中又有一个戈登增长模型Gordon Growth Model,也就是股利贴现模型,所以干脆简单说说这个DDM吧。
为了写这篇介绍,我特意翻出来了10多年前的课件,相比百度百科和MBA智库百科介绍,课件的内容更简单易懂。
在翻课件的时候,看到课件上有个图,总结了股权估值的方法,发现自己这些年来做的估值不过是九牛一毛。
上图中的三个贴现现金流法,自由现金流的现值就是我们前面模型使用的方法。
经营现金流的现值我没用来做过估值,现在普遍用的还是自由现金流来做贴现。
咱们说回股利贴现模型。
DDM归纳总结起来有三个版本,分别是0增长模型,永续增长模型和暂时超常增长模型。
1. 0增长模型(Zero-GrowthModel)顾名思义,股利的增长率为0,每年发放的股利保持不变。
公式是:其中k是投资者要求的投资回报率(required rate of return),也可以说是资金成本。
例如:某上市公司当年的分红是每股3块钱,投资者要求的投资回报率是17.5%,那么上市公司的股价应该是多少呢?V=¥3/0.175=¥17.52. 永续增长模型(InfinitePeriod Model)这个增长模型是假设股利按照一个固定不变的增长率逐年增长。
公式是:其中:D0为当期红利。
D0x(1+g)为下一期的红利k为投资者要求的投资回报率,即资金成本g 为固定的增长率例如:上面的示例中,每年的股利增长5%,那么股价应该是多少呢?V=¥3x(1+0.05)/(0.175-0.05)=¥25.23. 暂时超常增长模型(TemporarySupernormal Growth Model)这个更多的叫做多段增长模型,公式是:例如:某公司第一年的股利为2元/股,投资者要求的投资回报率为14%,未来10年的股利增长率如下表所示:年份股利增长率1-3 25%4-6 20%7-9 15%10及以后9% 套用公式来计算,就是这样的:把上面的公式放到EXCEL表格中,比较直观:在这个表中,需要特别说明的是第12行的红色字体。
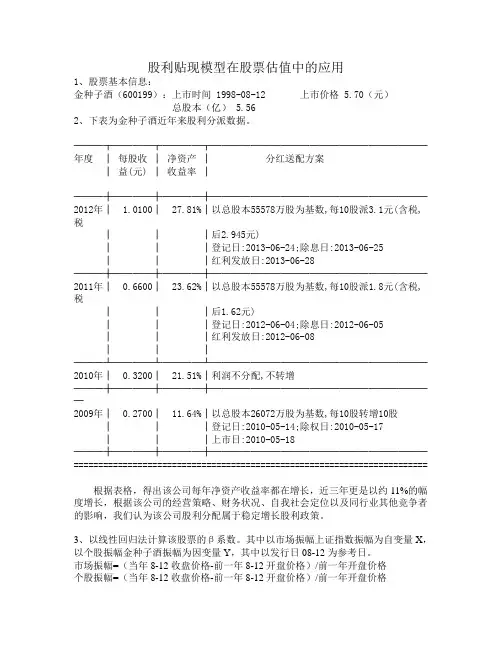
股利贴现模型在股票估值中的应用1、股票基本信息:金种子酒(600199):上市时间 1998-08-12 上市价格 5.70(元)总股本(亿) 5.562、下表为金种子酒近年来股利分派数据。
───┬────┬────┬──────────────────────年度│每股收│净资产│分红送配方案│益(元) │收益率│───┼────┼────┼──────────────────────2012年│ 1.0100│ 27.81%│以总股本55578万股为基数,每10股派3.1元(含税,税│││后2.945元) │││登记日:2013-06-24;除息日:2013-06-25 │││红利发放日:2013-06-28 ───┼────┼────┼──────────────────────2011年│ 0.6600│ 23.62%│以总股本55578万股为基数,每10股派1.8元(含税,税│││后1.62元) │││登记日:2012-06-04;除息日:2012-06-05 │││红利发放日:2012-06-08 │││───┴────┴────┴──────────────────────2010年│ 0.3200│ 21.51%│利润不分配,不转增───┼────┼────┼───────────────────────2009年│ 0.2700│ 11.64%│以总股本26072万股为基数,每10股转增10股│││登记日:2010-05-14;除权日:2010-05-17 │││上市日:2010-05-18 ───┼────┼────┼──────────────────────========================================================================根据表格,得出该公司每年净资产收益率都在增长,近三年更是以约11%的幅度增长,根据该公司的经营策略、财务状况、自我社会定位以及同行业其他竞争者的影响,我们认为该公司股利分配属于稳定增长股利政策。



1. 股利折现模型(The Dividend Discount Model, DDM)股票的现金流可以分为两个部分:股利的收入及股价的变动先来定义Pt:第t期的每股股价Dt:第t期的每股股利Rs:股利折现率(或称为股东的必要报酬率)当下的股票现值P0 = D1/(1+Rs) + P1/(1+Rs) (1)一年后的股票现值P1 = D2/(1+Rs) + P2/(1+Rs) (2)将(1)代入(2)可得P0 = D1/(1+Rs) + D2/[(1+Rs) ^2] + P2/[(1+Rs)^2]可推得P0 = D1/(1+Rs) + D2/[(1+Rs) ^2] + D3/[(1+Rs)^3] + ... =SIGMA(t=1, infinite) D1/[(1+Rs)^t]常见的股利折现模型有叁种,a.零成长型(Zero Growth), 即D1=D2=D3=...利用等比级数公式, a0=D1/(1+Rs), r= 1/(1+Rs) =>p0 = D1/Rs[*这跟永续年金的结果相同]b.固定成长(Constant Growth), 即股利按固定比率g成长,D2=D1*(1+g), ...=> P0 = D1/(Rs-g)b.1这个模型又称为戈登模型(Gordon Model)或股利成长模型(dividend growth model)因为这个模型提供我们很好的直觉:b.1.1 当公司宣布年底股利增加, D1上升, P0上升b.1.2 当公司盈余成长, g上升, P0上升b.1.3 当资本或风险提升,Rs上升, P0下降b.2固定成长型的资本利得率=股利成长率, g = (P0-P1)/P0c.超成长型(Supernormal or Nonconstant Growth), 即一开始公司有高成长率,几年后才回到一般成长。
EX. yahoo公司预期未来四年有高度成长25%, 之后皆以8%稳定成长, 其折现率20%. 今发行4块股利:这边P0需分为两个部分, 一为超成长部分及稳定成长部分.I. P0(超) = D1/(1+Rs) + D2/(1+Rs)^2 + D3/(1+Rs)^3 + D4/(1+Rs)^4II. 在第四年时, 其未来股利现值PV4为D5/(1+Rs)+D6/(1+Rs)^2 + ...其中D5 = D4*1.08, 可套用固定成长模型公式得PV4 = D5/(Rs-g)再将PV4折现到P0(稳定)= PV4/(1+Rs)^4关于股价折现模型(DDM)的参数g与Rs, 可以利用会计资讯做简单的推估:(1) 使用ROE法(Return on Equity)推估股利成长率gSales-Cost- Exp--------------EBDITA- Debt(折旧费用)----------------EBIT(息前税前盈余)- I(利息费用)----------------EBT(税前盈余)- T---------------- EB(税后盈余或净利)需要记忆的几个说词:1. 税后净利NI可以分做股利或保留盈余2. 股利发放率dividends payout ratio, d = Total dividends/ NI3. 盈余保留率Retain ratio = 1-d4. 当年度股东权益报酬ROE(Return on Equity) = NI / Total Equity5. 若有N股流通在外股数(Number of share outstanding), 可计算EPS, earning per share = NI/NDPS, total dividends/ N=> d = total dividends/NI = DPS/EPS在没有新的筹募资金下,公司下一年的盈余=今年盈余+保留盈余x保留盈余报酬率除以今年盈余可得1+g = 1 + 盈余保留率x保留盈余报酬率=> g = 盈余保留率x保留盈余报酬率*Ross建议使用ROE替代保留盈余报酬率,因此g=盈余保留率x ROE =>当股利发放率每年是相同时,盈余成长率g = 股利成长率(2)使用Gordon模型推估Rs : P0 = D1/(Rs-g) => Rs = D1/P0 + g.。


股利贴现模型其中V为每股股票的内在价值,Dt是第t年每股股票股利的期望值,k是股票的期望收益率或贴现率(discount rate)。
公式表明,股票的内在价值是其逐年期望股利的现值之和。
根据一些特别的股利发放方式,DDM模型还有以下几种简化了的公式:←零增长模型←即股利增长率为0,未来各期股利按固定数额发放。
计算公式为:V=D0/k其中V为公司价值,D0为当期股利,K为投资者要求的投资回报率,或资本成本。
零增长模型即股利增长率为0,未来各期股利按固定数额发放。
计算公式为:V=D0/k其中V为公司价值,D0为当期股利,K为投资者要求的投资回报率,或资本成本。
不变增长模型即股利按照固定的增长率g增长。
计算公式为:V=D1/(k-g)注意此处的D1=D0(1+g)为下一期的股利,而非当期股利。
二段、三段、多段增长模型二段增长模型假设在时间l内红利按照g1增长率增长,l外按照g2增长。
三段增长模型也是类似,不过多假设一个时间点l2,增加一个增长率g3优先股:一、优先股通常预先定明股息收益率。
由于优先股股息率事先固定,所以优先股的股息一般不会根据公司经营情况而增减,而且一般也不能参与公司的分红,但优先股可以先于普通股获得股息,对公司来说,由于股息固定,它不影响公司的利润分配。
二、优先股的权利范围小。
优先股股东一般没有选举权和被选举权,对股份公司的重大经营无投票权,但在某些情况下可以享有投票权。
三、如果公司股东大会需要讨论与优先股有关的索偿权,即优先股的索偿权先于普通股,而次于债权人。
第三年现金流较复杂,包括股利和类似优先股的最终价值。
(2)假定股票价格为26元,计算股票的预期收益率。
利用插值法插值法又称“内插法”,是利用函数f (x)在某区间中若干点的函数值,作出适当的特定函数,在这些点上取已知值,在区间的其他点上用这特定函数的值作为函数 f (x)的近似值,这种方法称为插值法。
因为26 > 25.1,所以贴现率一定小于第一问中的10%,试着用8%算,最终用插值法算出9.68%解决方案1:一年股利=2*(1+8%)=2.098)=(10%-9%)/,股票价值=2.942;(26-25.098当要求的报酬率是9%时.333/.16/.333第三年股利=2.098(2)股票价格26元.16第二年股利=2.16*(1+8%)=2,(i-10%)/,股票价值是25.333/.098-27;(25.942);(1+9%)^2+2.566/(1+9%)+2,当要求的报酬率是10%时.566……(1)股票价值=2.16/.3328*(1+10%)=2;[10%*(1+10%)^2]=25.566第四年股利=2,i=9;[9%*(1+9%)^2]=27;(1+10%)+2;(1+10%)^2+2,运用差值法.68%股票预期收益率是9.566/股利贴现模型股利贴现模型其中V为每股股票的内在价值,Dt是第t年每股股票股利的期望值,k是股票的期望收益率或贴现率(discount rate)。