量子力学第四章-表象理论(3部分)
- 格式:ppt
- 大小:1.95 MB
- 文档页数:66



量子力学讲义第4章第四章量子力学的表述形式(本章对初学者来讲是难点)表象:量子力学中态和力学量的具体表示形式。
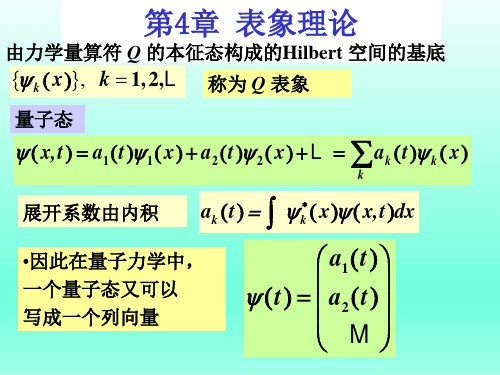
为了便于理解本章内容,我们先进行一下类比:矢量(欧几里德空间)量子力学的态(希尔伯特空间)基矢),,(321e e e~三维本征函数,...),...,,(21n ψψψ~无限维任意矢展开∑=ii i e A A任意态展开∑=nn n a ψψ),,(z y x e e e),...)(),...,(),((21x x x n ψψψ 取不同坐标系),,(?θe e e r取不同表象),...)(),...,(),((21p C p C p C n ………. ………. 不同坐标之间可以进行变换不同表象之间可以进行变换由此可见,可以类似于矢量A,将量子力学“几何化”→在矢量空间中建立它的一般形式。
为此,我们将① 引进量子力学的矢量空间~希尔伯特空间;② 给出态和力学量算符在该空间的表示;③ 建立各种不同表示之间的变换关系。
最后介绍一个典型应用(谐振子的粒子数表象)和量子力学的三种绘景。
4.1希尔伯特空间狄拉克符号狄拉克符号“”~类比:),,(z y x A A A欧氏空间的矢量 A→坐标系中的分量),,(?θA A A r……….)(rψ →表象下的表示)(p C……….引入狄拉克符号的优点:①运算简洁;②勿需采用具体表象讨论。
一、希尔伯特空间的矢量定义:希尔伯特空间是定义在复数域上的、完备的、线性内积空间,并且一般是无限维的。
1、线性:①c b a =+;②a b λ=。
2、完备性:∑=nn n a a 。
3、内积空间:引入与右矢空间相互共轭的左矢空间∑==?+nn n a a a a *;)(:。
定义内积:==*ab b a 复数,0≥a a 。
1=a a ~归一化;b a b a ,~0=正交;m n n m δ=~正交归一;)(x x x x '-='δ~连续谱的正交归一。


量⼦⼒学讲义IV.表象理论(矩阵表述)IV. 表象理论 ( 矩阵表述 )1.如何⽤矩阵表⽰量⼦态与⼒学量,并说明理由?答:矩阵表⽰⼀般⽤于本征值为离散谱的表象(相应的希尔伯空间维数是可数的)。
具体说,如果⼒学量的本征⽮为,相应本征值分别为。
假定⼀个任意态⽮为,将它展开For personal use only in study and research; not for commercial use则态⽮在表象中波函数便可⽤展开系数的⼀列矩阵表⽰其意义是:在态中,取的概率为,这与表象中波函数意义是类似的。
⼒学量⽤厄⽶⽅阵表⽰,。
显然,⼀列矩阵和⽅阵维数与希尔伯空间维数是相等的。
⽤矩阵表⽰⼒学量,有如下理由:第⼀可以反映⼒学量作⽤于⼀个量⼦态得到另⼀个量⼦态的事实。
设,式中,。
取,两端左乘,取标积得,即第⼆矩阵乘法⼀般不满⾜交换率,这恰好能满⾜两个⼒学量⼀般不对易的要求。
第三厄⽶矩阵的性质能体现⼒学量算符的厄⽶性。
对于本征值为连续谱的表象(希尔伯空间维数不可数),也可形式的运⽤矩阵表⽰,这时可将矩阵元素看成式连续分布的。
2.量⼦⼒学中,不同表象间:基⽮、波函数、⼒学量是如何变换的?答:量⼦⼒学中由⼀个表象到另⼀个表象的变换为⼳正变换,它类似于欧⽒空间中坐标转动。
设表象中的基⽮为表象中的基⽮为(1) 基⽮变换关系为式中,(为⼳正矩阵)。
设有任意态,则态在及表象中波函数分别为矩阵。
(2) 波函数变换规则为:矩阵。
(3) ⼒学量变换规则为:。
(式中与为⼒学量在、表象中矩阵)3.正变换有什么特征?答:⼳正变换特点:(1⼳正变换不改变态⽮的模,这⼀特征相当于坐标旋转变换;(2⼳正变换不改变⼒学量本征值;(3)⼒学量矩阵之迹 TrF与矩阵⾏列式 dgtF亦不因⼳正变换⽽改变.4. 学量在其⾃⾝表象中如何表⽰?其本征⽮是什么 ?答:如果⼒学量本征值为离散谱,那么,它在其⾃⾝表象中表⽰式为对⾓矩阵,为诸本征值。
本征⽮为单元素⼀列矩阵如果⼒学量本征值为连续谱,则它在其⾃⾝表象中为纯变量其本征⽮为函数。
第四章 表象理论4.1 态的表象变换和态的矩阵表示1.态的表象变换将F 表象中的态函数对力学量算符ˆQ 在F 表象中的本征函数组展开,则展开系数就是在Q 表象中的态函数。
这就是将F 表象中的态函数变换到Q 表象中的态函数的方法。
为了便于求出展开系数,通常要求ˆQ的本征函数组为幺正基组。
以从r 表象变换到Q 表象为例。
r 表象中的态函数为(,)r t ϕ [或()r ϕ]。
设ˆQ的本征值为分立谱Q n ,对应的本征函数为()n r φ 。
当各Q n 都无简并时,(,)r t ϕ 对()n r φ的展开式为:(,)()()n n nr t a t r ϕφ=∑(4.1-1) 若Q n 表示几个对易力学量算符本征值的集合,则上式中的n 应表示几个对应的量子数的集合。
当Q n 存在简并时,展开式为:(,)()()iiin n n r t a t r ϕφ=∑(4.1-2)其中i 为描写简并的角标。
下面只讨论无简并的情况。
在(4.1-1)式中,a n (t)是Q n 与t 的函数,a n (t)相当于a(Q n ,t)的简写。
当Q n 在整个展开系数中变动。
由于Q n 为分立谱,所以函数关系a n (t)-Q n 不是连续的。
a n (t)就是(,)r t ϕ 变换到Q表象中的态函数。
例如,将r表象中的某态函数(,,)r ϕθϕ对2ˆL 与ˆzL 的共同本征函数组(,)lm Y θφ展开: 0(,,)()(,)llm lm l m lr C r Y ϕθφθϕ∞==-=∑∑ (4.1-3)上式相当于(4.1-1)式中的n 表示两个量子数lm 的集合。
上式中的()lm C r 就是在2L 与z L 共同表象中的态函数。
2.本征态的排序本征态的排序可以化为对应的本征值的排序。
若本征值无简并,则参与排序的本征值没有相同者;若本征值有简并,则参与排序的本征值有相同者,其相同本征值的个数应与该本征值的简并度相同。
专题讲座4-表象理论一、狄拉克符号和表象我们用一个矢量ψ(右矢)来表示量子力学的一个状态, 这个状态可以用一套基矢量{}α来展开(某个算苻本征矢或几个的共同本征矢,基矢量是正交、归一完备的),选定一套基对应选定一个表象在本征值是分立时,nn naαψ=∑n n a α=ψ用一个列矩阵来表示展开系数12...n a a a ⎛⎫⎪ ⎪ ⎪ψ= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭这称为在这个表象中的波函数也可以用左矢ψ来表示状态*n n na ψ=∑ **()n n n a αα=ψ=ψ在{α表象中ψ用ψ的转置共轭矩阵表示(行矩阵)()†***12....n a a a ψ=右矢和左矢的标积定义为()12†****12....... .n n n n n a a b b b b a a ⎛⎫⎪ ⎪⎪Φψ=Φψ== ⎪ ⎪ ⎪⎝⎭∑ 态的归一化可以表示为()12†****12...1.n n n nn a a a a a a a a ⎛⎫⎪ ⎪ψψ=ψψ=== ⎪ ⎪⎝⎭∑在连续谱情况时,(比如坐标的本征矢x ,动量的本征矢p )()x x dx ψ=ψ⎰()x x ψ=ψ (这就是我们熟悉的坐标表象的波函数)*()()x x dx Φψ=Φψ⎰态的归一化可以表示为*()()1x x dx ψψ=ψψ=⎰当一个算苻作用在一个态上,它的作用是是这个态变成了另外一个态F Φ=ψ在一个算苻Q 的表示里(利用本征矢的封闭性1k k kαα=∑)k k m m mF ααααΦ=ψ∑即n nm m b F a = 1,2,3,...m =写成矩阵形式1111211221222212. .. ..... . ... . . . . . . . .n n n n n nn n b F F F a b F F F a b F F F a ⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎪= ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭其中算苻F 矩阵元为km k mF F αα=要具体计算出来,一般可以借助Q 在坐标表象的本征函数'''*'''*()(,/)()()()(,/)()km k m k m k m k m F F x x F x x dx dxx F x i x x x x dx dx x F x i x x dxααααδααα===-∂∂-=-∂∂⎰⎰⎰⎰⎰本征态方程F ψλψ=在Q 表象1112111212222212.... ......... . . . . . . .n n n n nn n n F F F F F F F F F ββββλββ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪=⎪⎪ ⎪ ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭(在坐标表象 (,/)()()F x i x x x ψλψ-∂∂= )久期方程11121111121212222212221212... .... . .....0..... .... . . . . . . . . n n n n n n nn n n n nn F F F F F F F F F F F F F F F F F F λβλλβλλβλ--⎛⎫⎛⎫ ⎪⎪-- ⎪⎪ ⎪⎪=→⎪⎪-- ⎪⎪ ⎪⎪⎝⎭⎝⎭0 . . . .= 表象变换设算苻A 的本征矢为{}m a , 算苻B 的本征矢为{}b αb α可以用{}ma 展开m m mb S a αα=∑展开系数*()()m m m m S a b dx a x x b dxa x b x αααα===⎰⎰以m S α为矩阵元的矩阵成为变换矩阵。