量子力学的矩阵形式及表象理论

§4.5 量子力学的矩阵形式和表象变换态和力学量算符的不同表示形式称为表象。

态有时称为态矢量。

力学量算符对态的作用实际上是对矢量量进行变换，因此可与代数中线性变换进行类比。

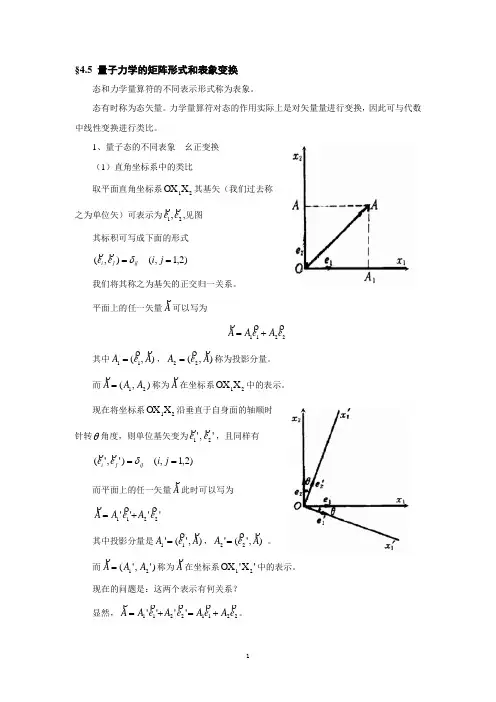
1、量子态的不同表象 幺正变换（1）直角坐标系中的类比取平面直角坐标系21X OX 其基矢（我们过去称之为单位矢）可表示为21,e e,见图其标积可写成下面的形式)2,1,(),(==j i e e ijj i δ我们将其称之为基矢的正交归一关系。

平面上的任一矢量A可以写为2211e A e A A +=其中),(11A e A =，),(22A e A=称为投影分量。

而),(21A A A = 称为A在坐标系21XOX 中的表示。

现在将坐标系21X OX 沿垂直于自身面的轴顺时针转θ角度，则单位基矢变为','21e e，且同样有)2,1,()','(==j i e e ijj i δ而平面上的任一矢量A此时可以写为 ''''2211e A e A A +=其中投影分量是),'('11A e A=，),'('22A e A =。

而)','(21A A A = 称为A在坐标系'X 'OX21中的表示。

现在的问题是：这两个表示有何关系？显然，22112211''''e A e A e A e A A+=+=。

用'1e 、'2e分别与上式中的后一等式点积（即作标积），有),'(),'('2121111e e A e e A A+= ),'(),'('2221212e e A e e A A+=表成矩阵的形式为⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛212212211121),'(),'(),'(),'(''A A e e e e e e e e A A由于'1e、1e及'2e、2e的夹角为θ，显然有⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛21212212211121cos sin sin cos ),'(),'(),'(),'(''A A A A e e e e e e e e A A θθθθ或记为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛2121)(''A A R A A θ 其中⎪⎪⎭⎫⎝⎛-=θθθθθcos sin sin cos )(R 是把A在两坐标中的表示⎪⎪⎭⎫⎝⎛''21A A 和⎪⎪⎭⎫⎝⎛21A A 联系起来的变换矩阵。

第4章 量子力学的矩阵形式与表象变换§1 量子态的不同表象态的表象 量子力学中态和力学量的具体表示方式研究表象的意义 根据不同问题选择不同表象，还可以进行表象变换。

一、坐标表象波函数ψ(x ,t ) 1、ψ(x ,t )2、dx t x 2),(ψ——表示体系处在ψ(x ,t )所描述的态中，在x →x +d x 范围内找到粒子的几率，也就是说，当体系处在ψ(x ,t )所描述的态中，测量坐标x 这个力学量所得值在x →x +d x 这个范围内的几率。

3、2(,)1x t dx ψ=⎰4、动量为x p '的自由粒子的本征函数 xp ip e x ''=2/1)2(1)(πψ5、x 在坐标表象中对应于本征值x '的本征函数)(x x '-δ， 即，)()(x x x x x x '-'='-δδ 二、动量表象波函数 动量本征函数：pxip e x2/1)2(1)(πψ=组成完备系，任一状态ψ可按其展开(,)(,)()p x t c p t x dp ψψ=⎰ (1) 展开系数*(,)()(,)pc p t x x t dx ψψ=⎰ (2) ψ(x ,t )与c (p ,t )互为Fourier （付里叶）变换，一一对应关系，所不同的是变量不同。

认为c (p ,t )和ψ(x ,t )描述同一个状态。

ψ(x ,t )是这个状态在坐标表象中的波函数，c (p ,t )是同一个状态在动量表象中的波函数。

1、),(t p c ——状态波函数2、dp t p c 2),(表示体系处在c (p ,t )所描述的态中测量动量这个力学量p 所得结果为p →p +d p 范围内的几率。

3、1),(2=⎰dp t p c命题：假设ψ(x ,t )是归一化波函数，则c (p ,t )也是归一。

(在第一章中已经证明) 4、x p '的本征函数（具有确定动量x p '的自由粒子的态）若ψ(x ,t )描写的态是具有确定动量 p'的自由粒子态，即：1/21()(2)ip xp x eψπ''=则相应动量表象中的波函数：*(,)()(,)pc p t x x t dx ψψ=⎰()p i E te p p δ'-'=-所以，在动量表象中，具有确定动量p' 的粒子的波函数是以动量p 为变量的δ函数。

量⼦⼒学讲义IV.表象理论（矩阵表述）IV. 表象理论 ( 矩阵表述 )1．如何⽤矩阵表⽰量⼦态与⼒学量，并说明理由？答：矩阵表⽰⼀般⽤于本征值为离散谱的表象（相应的希尔伯空间维数是可数的）。

具体说，如果⼒学量的本征⽮为，相应本征值分别为。

假定⼀个任意态⽮为，将它展开For personal use only in study and research; not for commercial use则态⽮在表象中波函数便可⽤展开系数的⼀列矩阵表⽰其意义是：在态中，取的概率为，这与表象中波函数意义是类似的。

⼒学量⽤厄⽶⽅阵表⽰，。

显然，⼀列矩阵和⽅阵维数与希尔伯空间维数是相等的。

⽤矩阵表⽰⼒学量，有如下理由：第⼀可以反映⼒学量作⽤于⼀个量⼦态得到另⼀个量⼦态的事实。

设，式中，。

取，两端左乘，取标积得，即第⼆矩阵乘法⼀般不满⾜交换率，这恰好能满⾜两个⼒学量⼀般不对易的要求。

第三厄⽶矩阵的性质能体现⼒学量算符的厄⽶性。

对于本征值为连续谱的表象（希尔伯空间维数不可数），也可形式的运⽤矩阵表⽰，这时可将矩阵元素看成式连续分布的。

2.量⼦⼒学中，不同表象间：基⽮、波函数、⼒学量是如何变换的？答：量⼦⼒学中由⼀个表象到另⼀个表象的变换为⼳正变换，它类似于欧⽒空间中坐标转动。

设表象中的基⽮为表象中的基⽮为(1) 基⽮变换关系为式中，（为⼳正矩阵）。

设有任意态，则态在及表象中波函数分别为矩阵。

(2) 波函数变换规则为：矩阵。

(3) ⼒学量变换规则为：。

（式中与为⼒学量在、表象中矩阵）3.正变换有什么特征？答：⼳正变换特点：(1⼳正变换不改变态⽮的模，这⼀特征相当于坐标旋转变换；(2⼳正变换不改变⼒学量本征值；(3)⼒学量矩阵之迹 TrF与矩阵⾏列式 dgtF亦不因⼳正变换⽽改变．4. 学量在其⾃⾝表象中如何表⽰？其本征⽮是什么 ?答：如果⼒学量本征值为离散谱，那么，它在其⾃⾝表象中表⽰式为对⾓矩阵，为诸本征值。

本征⽮为单元素⼀列矩阵如果⼒学量本征值为连续谱，则它在其⾃⾝表象中为纯变量其本征⽮为函数。

第六章量子力学的矩阵形式及表示理论第六章目录§6.1 量子体系状态的表示 (3)§6.2 Dirac符号介绍 (4)（1）量子态、Ket矢，Bra矢（Bracket） . 5（2）标积 5（3）算符及其表示 (7)（4）不可约张量算符的矩阵元计算简介 (12)（5）投影算符 15§6.3 表象变换，幺正变换 (17)（1）同一状态在不同表象中的表示间的关系 (17)（2）两表象的基矢之间关系 (18)（3）力学量在不同表象中的矩阵表示之间的关系 (18)（4）幺正变换 19§6.4平均值，本征方程和薛定谔方程的矩阵形式 (20)（1）平均值20（2）本征方程 21（3）薛定谔方程 (25)§6.5 量子态的不同描述 (26)（1）薛定谔绘景 (27)（2）海森堡绘景 (28)第六章 量子力学的矩阵形式及表示理论§6.1 量子体系状态的表示现在来讨论体系状态的“坐标”—状态表示如果有一组力学量Mˆ构成一力学量完全集，其共同本征函数构成一正交，归一和完备组，并有封闭性。

()mn n m ,δ=ϕϕ)r r ()r ()r (*m mm '-δ='ϕϕ∑于是，任一波函数⎰''ψ'-δ=ψr d )r ()r r ()r (⎰∑''ψ'ϕϕ=r d )r ()r ()r (m*m m∑ϕ=mm m a )r (。

⎰ψϕ=''ψ'ϕ=),(r d )r ()r (a m *m m2m a 是在)r (ψ中测得力学量M ˆ取值为m 的几率（若)r (ψ是归一化的）。

显然，当选定一组力学量完全集Mˆ 后，则集合 {}m a 是与 )r (ψ 完全等价的，它完全确定了体系的状态。

我们将会看到，{}m a 与)r (ψ一样，提供给我们同样多的信息。

状态表示的定义：若力学量的完全集M ˆ的共同本征函数组为m ϕ，则),(a m mψϕ=的全体{}m a ，被称为体系所处态ψ在Mˆ表象中的表示，也可以看作态矢量ψ在m ϕ作为基矢所张的“坐标系”中的“坐标”。

第四章矩阵力学基础(Ⅱ)——表象理论4.1态和算符的表象表示1．态的表象表示 (1) 坐标表象以坐标算符的本征态为基底构成的表象称为坐标表象。

以一维的x 坐标为例。

算符xˆ本征方程是)()(ˆx x x x x x'-'='-δδ (4-1-1) 本征函数是).(x x '-δ量子态)(x 'ψ总可按x 的本征函数系展开，得dxx x x x )()()('-='⎰δϕϕ （4.1.2）展开系数必)(x ϕ就是该量子态在x 表象的表示，即波函数。

(2) 动量表象以动量算符的本征态为基底构成的表象是动量表象。

选x 为自变量，动量算符的本征函数是平面波。

以动量算符x pˆ为例，其本征态为： x p ip x x ex2121=/)()(πϕ (4 .1 .3)将量子态)(x ϕ按)(x xp ϕ展开==⎰x p x dp x p C x x )()()(ψϕxx x p i dp p C ex )()(/⎰2121π (4 .1 .4)C(p x )就是动量表象中的波函数。

这正是第二章中已熟知的结果。

动量表象也可以用动量为自变量表示。

在P x 表象中，粒子具有确定动量分量P x 的波函数是以P x 为自变量的函数)()(ˆx x x x x x p p p p p p'-'='-δδ （4.1.5） 在动量表象中的波函数也可以用类似于(4. 1. 2)式的方式给出。

(3) 任意表象设有某一线性厄米算符Q ˆ。

为叙述方便起见，假定算符Q ˆ具有分立本征值谱。

它的本征方程为)()(ˆr u Q r u Q nn n = (4.1.6) 将波函数),(t r ϕ按Q ˆ算符的正交归一本征函数系)}({r u展开∑=nn n r u t a t r )()(),(ϕ （4.1.7）展开系数{a n (t)}就是波函数必),(t rϕ在Q 表象中的表示。