量子力学的矩阵形式和表象变换.
- 格式:doc
- 大小:779.50 KB
- 文档页数:19


§4.5 量子力学的矩阵形式和表象变换态和力学量算符的不同表示形式称为表象。
态有时称为态矢量。
力学量算符对态的作用实际上是对矢量量进行变换,因此可与代数中线性变换进行类比。
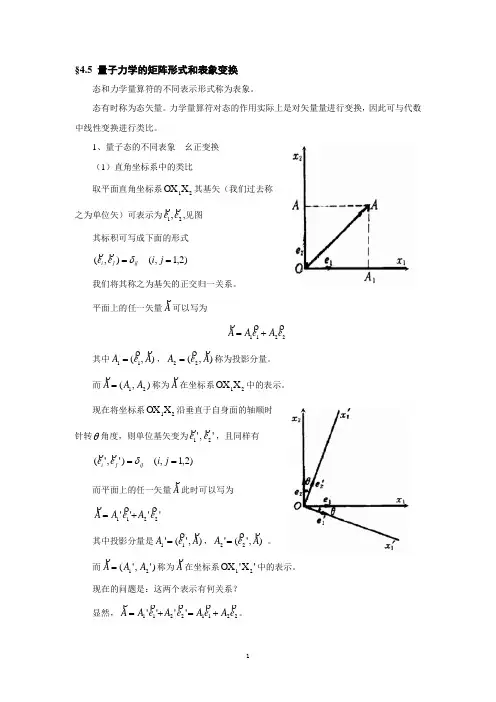
1、量子态的不同表象 幺正变换(1)直角坐标系中的类比取平面直角坐标系21X OX 其基矢(我们过去称之为单位矢)可表示为21,e e,见图其标积可写成下面的形式)2,1,(),(==j i e e ijj i δ我们将其称之为基矢的正交归一关系。
平面上的任一矢量A可以写为2211e A e A A +=其中),(11A e A =,),(22A e A=称为投影分量。
而),(21A A A = 称为A在坐标系21XOX 中的表示。
现在将坐标系21X OX 沿垂直于自身面的轴顺时针转θ角度,则单位基矢变为','21e e,且同样有)2,1,()','(==j i e e ijj i δ而平面上的任一矢量A此时可以写为 ''''2211e A e A A +=其中投影分量是),'('11A e A=,),'('22A e A =。
而)','(21A A A = 称为A在坐标系'X 'OX21中的表示。
现在的问题是:这两个表示有何关系?显然,22112211''''e A e A e A e A A+=+=。
用'1e 、'2e分别与上式中的后一等式点积(即作标积),有),'(),'('2121111e e A e e A A+= ),'(),'('2221212e e A e e A A+=表成矩阵的形式为⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛212212211121),'(),'(),'(),'(''A A e e e e e e e e A A由于'1e、1e及'2e、2e的夹角为θ,显然有⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛21212212211121cos sin sin cos ),'(),'(),'(),'(''A A A A e e e e e e e e A A θθθθ或记为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛2121)(''A A R A A θ 其中⎪⎪⎭⎫⎝⎛-=θθθθθcos sin sin cos )(R 是把A在两坐标中的表示⎪⎪⎭⎫⎝⎛''21A A 和⎪⎪⎭⎫⎝⎛21A A 联系起来的变换矩阵。




第4章 量子力学的矩阵形式与表象变换§1 量子态的不同表象态的表象 量子力学中态和力学量的具体表示方式研究表象的意义 根据不同问题选择不同表象,还可以进行表象变换。
一、坐标表象波函数ψ(x ,t ) 1、ψ(x ,t )2、dx t x 2),(ψ——表示体系处在ψ(x ,t )所描述的态中,在x →x +d x 范围内找到粒子的几率,也就是说,当体系处在ψ(x ,t )所描述的态中,测量坐标x 这个力学量所得值在x →x +d x 这个范围内的几率。
3、2(,)1x t dx ψ=⎰4、动量为x p '的自由粒子的本征函数 xp ip e x ''=2/1)2(1)(πψ5、x 在坐标表象中对应于本征值x '的本征函数)(x x '-δ, 即,)()(x x x x x x '-'='-δδ 二、动量表象波函数 动量本征函数:pxip e x2/1)2(1)(πψ=组成完备系,任一状态ψ可按其展开(,)(,)()p x t c p t x dp ψψ=⎰ (1) 展开系数*(,)()(,)pc p t x x t dx ψψ=⎰ (2) ψ(x ,t )与c (p ,t )互为Fourier (付里叶)变换,一一对应关系,所不同的是变量不同。
认为c (p ,t )和ψ(x ,t )描述同一个状态。
ψ(x ,t )是这个状态在坐标表象中的波函数,c (p ,t )是同一个状态在动量表象中的波函数。
1、),(t p c ——状态波函数2、dp t p c 2),(表示体系处在c (p ,t )所描述的态中测量动量这个力学量p 所得结果为p →p +d p 范围内的几率。
3、1),(2=⎰dp t p c命题:假设ψ(x ,t )是归一化波函数,则c (p ,t )也是归一。
(在第一章中已经证明) 4、x p '的本征函数(具有确定动量x p '的自由粒子的态)若ψ(x ,t )描写的态是具有确定动量 p'的自由粒子态,即:1/21()(2)ip xp x eψπ''=则相应动量表象中的波函数:*(,)()(,)pc p t x x t dx ψψ=⎰()p i E te p p δ'-'=-所以,在动量表象中,具有确定动量p' 的粒子的波函数是以动量p 为变量的δ函数。




§4.5 量子力学的矩阵形式和表象变换态和力学量算符的不同表示形式称为表象。
态有时称为态矢量。
力学量算符对态的作用实际上是对矢量量进行变换,因此可与代数中线性变换进行类比。
1、量子态的不同表象 幺正变换(1)直角坐标系中的类比取平面直角坐标系21X OX 其基矢(我们过去称之为单位矢)可表示为21,e e,见图其标积可写成下面的形式)2,1,(),(==j i e e ijj i δ我们将其称之为基矢的正交归一关系。
平面上的任一矢量A可以写为2211e A e A A +=其中),(11A e A =,),(22A e A=称为投影分量。
而),(21A A A = 称为A在坐标系21X OX 中的表示。
现在将坐标系21X OX 沿垂直于自身面的轴顺时针转θ角度,则单位基矢变为','21e e,且同样有)2,1,()','(==j i e e ijj i δ而平面上的任一矢量A此时可以写为''''2211e A e A A +=其中投影分量是),'('11A e A=,),'('22A e A =。
而)','(21A A A =称为A 在坐标系'X 'OX 21中的表示。
现在的问题是:这两个表示有何关系?显然,22112211''''e A e A e A e A A +=+=。
用'1e 、'2e分别与上式中的后一等式点积(即作标积),有),'(),'('2121111e e A e e A A+= ),'(),'('2221212e e A e e A A+=表成矩阵的形式为⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛212212211121),'(),'(),'(),'(''A A e e e e e e e e A A由于'1e 、1e 及'2e 、2e的夹角为θ,显然有⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛21212212211121cos sin sin cos ),'(),'(),'(),'(''A A A A e e e e e e e e A A θθθθ或记为⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛2121)(''A A R A A θ 其中⎪⎪⎭⎫⎝⎛-=θθθθθcos sin sin cos )(R 是把A在两坐标中的表示⎪⎪⎭⎫ ⎝⎛''21A A 和⎪⎪⎭⎫⎝⎛21A A 联系起来的变换矩阵。
变换矩阵的矩阵元正是两坐标系基矢间的标积,它表示基矢之间的关系。
故R 给定,任何矢量在两坐标系间的关系也确定。
很容易证明,R 具有下述性质:I R R R R ==~~由于1)(det )~det(2==R R R ,其中 321321)1()det(p p p tR R R R -∑=, 故称这种矩阵为正交矩阵。
但1det =R (对应于真转动(proper rotation ))且R R =*(实矩阵)1*~-+===∴R R R R I R R RR ==∴++我们把满足上述条件的矩阵叫幺正矩阵。
到现在为止,我们介绍了三种矩阵: 厄米矩阵:*~R R R ==+正交矩阵:I R R R R ==~~ 幺正矩阵:I R R RR ==++这三种矩阵在以后的学习中经常涉及到,请注意掌握。
(2)量子力学中的表象形式上与上述类似,在量子力学中,按照态的叠加原理,任何一个态ψ可以看成Hilbert 空间的一个“矢量”。
体系的力学量 F 完全集的共同本征函数系k ψ(k 代表一组完备量子数)构成一组正交归一完备基矢。
这组基矢构成的“坐标系”称为F 表象。
同样kj j k δψψ=),(对于任意态矢量ψ,有∑=kk k a ψψ其中),(ψψk k a =这一组系数)( ,,21a a 就是态(矢)在F 表象中的表示,它们分别是与各基矢的内积。
与代数不同的是:①这里的“矢量”(量子态)是复数; ②空间维数可以是无穷的,甚至不可数的。
现在考虑同一个态ψ在另一组力学量完全集'F (表象'F )中的表示。
设本征态为'αψ,满足正交归一,即αββαδψψ=)','(态ψ用这组态矢展开,即''αααψψ∑=a其展开系数为),'('ψψαα=a ,则这一组系数)( ,','21a a 就是态ψ在'F 表象中的表示。
那么)()( ,',',,2121a a a a ↔ ? 方法同前述。
因为显然kkk a a ψψψααα∑∑=='',对后一等式用'*αψ作内积,有∑∑==kk k kk k a S a a αααψψ),(''其中),(k k S ψψαα'=是'F 表象基矢与F 表象基矢的内积。
上式也可以写成矩阵的形式:⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛k a a a S S S S a a a 212221121121'''α 简记为Sa a ='通过S 矩阵相联系,且I S S SS ==++,即S 矩阵是幺正矩阵(下面将予以证明)。
它实际上是联系两个基矢的变换矩阵。
例 试证明: S 矩阵是幺正矩阵 [分析]只要证明S S +的矩阵元是kj δ即可。
在F 表象中,有∑∑==++ααααααj k j k kj S S S S S S *)(根据S 矩阵元的定义,上式为)'()()(')'(''d d )'()'(''d )()('d )(**33*3*3r r r r r r r r r r r r S S j k j k kjψψψψψψψψαααααα⎰⎰∑⎰∑⎰=⨯=+利用前面的介绍,δ函数可以用任何一组正交归一完备函数组来构成,即∑=-nn n x x x x )()'()'(*ψψδ则上式kjj k kj r r r r r r S S δψψδ=-=⎰⎰+)'()()'('d d )(*33可见,S S +矩阵为单位矩阵,即I S S =+。
2、力学量算符的矩阵表示 仍以线性空间的矢量作类比B A→(正向转动θ角)已经知道:),(212211A A A e A e A A =⇒+=),(212211B B B e B e B B =⇒+=令A R B)(θ=,写成分量的形式,有22112211e R A e R A e B e B +=+用21e e、对上式点乘,得)()(2121111e R e A e R e A B,,+= )()(2221212e R e A e R e A B,,+=即⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛212212211121)()()()(A A e R e e R e e R e e R e B B,,,, 按照右下图,有⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛2121212212211121)(cos sin sin cos )()()()(A A R A A A A e R e e R e e R e e R e B B θθθθθ,,,,其中⎪⎪⎭⎫⎝⎛-=θθθθθcos sin sin cos )(R 。
与此类比,设ψ经算符Lˆ作用后变成ϕ,即 ψϕLˆ= 以F 表象(力学量F 完全集的本征态k ψ)为基矢,即∑=kk k b ψϕ,∑=kk k a ψψ则有∑∑=kkk kkk L a b ψψˆ 下面我们看如何通过上式由k a 求k b 。
对∑∑=kkk kkk L a b ψψˆ,以),( j ψ作标积,得 kkjk k kk j j a L a L b ∑∑==)ˆ,(ψψ 其中)ˆ,(kj jk L L ψψ=。
由上式可见,力学量算符对态的作用可以写成⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛ 212221121121a a L L L L b b因此,)(jk L 矩阵一旦确定,则所有基矢(因而任何矢量)在Lˆ作用下的变化也就完全确定了。
例 求一维谐振子坐标 x 、动量 p 以及Hamiltonian H 在能量表象中的表示。
[分析]:不同体系的Hamiltonian 不一样,能量表象的基矢也不一样。
这里能量表象的基矢为一维谐振子Hamiltonian 的本征函数)(x n ψ。
解:利用一维谐振子波函数的递推关系⎥⎦⎤⎢⎣⎡++=+-112121n n n n n x ψψαψ⎥⎦⎤⎢⎣⎡+-=+-11212d d n n n n n x ψψαψ所以⎥⎦⎤⎢⎣⎡++==-+1,1,2211),(n m n m n m mn nn x x δδαψψ⎥⎦⎤⎢⎣⎡-+=-=-+1,1,221)d d ,(n m n m n m mnnn i x i p δδαψψ注意:这里的m 、n 都是由0开始取值。
这样⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=02/3002/30100102/1002/101)(αmn x ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---=02/3002/30100102/1002/10)(αi p mn 而mnmn n n m mn n E H H ωδδψψ )21()ˆ,(+=== 所以⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛= 2/70002/500002/300002/1)(ωmn H 是一个对角矩阵。
任何力学量在自身表象中的表示都是对角矩阵。
3、量子力学的矩阵表示设力学量完全集F 的本征态是分立的(基矢可数),在F 表象中,力学量L 用矩阵表示为)(kj L ,且)ˆ,(jk kj L L ψψ=而量子态ψ则表示成列矢的形式,即⎪⎪⎪⎭⎫ ⎝⎛ 21a a ,其中),(ψψk k a =这样,量子力学的理论表述均可表成矩阵的形式。
下面我们分别讨论Schrödinger 方程、平均值公式以及本征值方程的矩阵形式。
(1) Schrödinger 方程ψψH ti =∂∂在F 表象中,∑=kkk t a t ψψ)()(,系数为时间t 的函数。