量子力学中几种表象及其之间的关系
摘要
体系的态可以用以坐标为变量的波函数ψ(x,t)来描写，力学量则以作用在这种波函数上的算符（量子力学中的算符代表对波函数的一种运算）来表示，这是量子力学中态和力学量的一种具体表述方式。态还可以用其他变量的函数作为波函数来描写体系的状态。 微观粒子体系的状态（量子态）和力学量的具体表示形式称为表象。 常用的表象有坐标表象、动量表象和能量表象。
而研究量子力学规律的各种表示形式以及这些不同形式之间的变换的理论，则称为表象理论。 关键词
态的表象 坐标表象 动量表象 Q 表象 算符表象 角动量表象 正文
体系的态既可用以x （表示全部坐标变量）为变量的波函数ψ(x,t)来描写，也可用以动量p 为变量的波函数c(p,t)来描写。ψ(x,t)和c(p,t)之间的变换关系是
式中 是动量的本征函数，
dx
x t x t p c dp x t p c t x p p )(),(),()(),(),(*ψ?=?=ψψψ
/2
/1)2(1)(ipx p e
x -=πψ
称ψ(x,t)是在坐标表象中的波函数，而c(p,t)是同一态在动量表象中的波函数。
由ψ(x,t)可知，粒子坐标在x 到x+dx 之间的概率
c 由(p,t ）可知，粒子动量在p 到p+dp 之间的概率
如果ψ(x,t)所描写的状态是具有动量p ’的自由粒子的状态，即ψ(x,t)=ψp ’(x,t),则
在动量表象中，粒子具有确定动量p ’的波函数是以动量p 为变量的δ函数。
那么，态在任意力学量Q 的表象中的描写方式又是什么样呢？ 设力学量Q 具有分立的本征值Q1,Q2,…Qn …，对应的本征函数为u1(x),u2(x),…,un(x),…,并组成正交归一的完全系。将态在坐标表象中的波函数ψ(x,t)按{un(x)}展开成
dx t x dx t x w 2
),(),(ψ=dp
t p c dp t p w 2
),(),(=dx e x x dx x t x t p c t iEp p
p p p
/''')()()(),(),(-**?=ψ?=ψψψ
/')'(t iEp e p p --=δ)
()(),(x u t a t x n n
n ∑=ψ
上式两边乘 ，再对x 变化整个空间积分 即
其物理意义是，体系处在ψ(x,t)所描述的状态时，力学量Q 具有确定值Qn 的几率为
可以用一组数
代替ψ(x,t)描写该状态。称{an （t ）}是该状态在Q 表象中的波函数。 如果Q 的全部本征值Q λ组成连续谱，对应本征函数是u λ（x ）则ψ(x,t)按u λ（x ）展开的式子为
a λ(t)就是Q 表象中的波函数，坐标表象、动量表象就属于这类表象。
从上面的叙述可以看出，同一状态可以用不同表象中的波函数来描写。表象的概念与几何学中坐标系的概念类似。 一个特定的Q 表象→一个特定的坐标系 本征函数→基矢
波函数是态矢量ψ在各基矢方向“分量”→坐标分量
)
()()()()()(),(t a t a dx t a x u x u dx x u t x m mn n
n n n n
m m ==?=ψ?∑∑*
*δdx
x u t x t a n n )(),()(*
ψ?=2
)
(),(t a t Q w n n ={})
),(,),(),(()(21??????=t a t a t a t a n n λ
λλd t u t a t x )()(),(?=ψ
写力学量的算符的表示方式随表象不同而改变。
设在x 表象中，算符 作用于波函数ψ(x,t)后得到一新的波函数
并设在Q 表象中波函数ψ(x,t)和Φ（x,t ）分别以{a1(t),a2(t),…,an(t),…} 和{b1(t),b2(t),…,bn(t),…}表示,un(x)为 本征函数，则可得
以 乘等式两边，再对整个空间积分，得
{Fmn}就是算符 在Q 表象中的表示。
{Fmn}可排列为一矩阵，Fmn 代表第m 行n 列元素，
在 的本征值组成连续谱的情况下，
也可看作是矩阵元。
),(),(),(t x x
i x F t x ψ??
-=Φ∧
∑∑∧
??
-=n
n n n n n x u x i x F t a x u t b )(),()()()( )
,2,1(,)(),()()
,2,1(),()(???=??
-?=???==∧
*∑m dx x u x
i x F x u F m t a F t b n m
mn n n
mn m 其中
???????
?
?
?????
???
??????????????????
????????=nn n n n n mn F F F F F F F F F F 2122221
11211}{dx
x u x
i x F x u F )(),()(''λλλ
λ??
-?=∧
如动量表象中算符 的矩阵元为 坐标表象中，算符 的矩阵元为
坐标表象
()()()2
2
2
,,,2i x t V x t x t t m x ψψ????=-+??????
对),(t x V 不显含时间t ，则
),(t x ψ 可以分离变量x 与t
()()
/
,iEt x t e
x ψψ-=
并设()x n ψ是正交归一的，即
()()*
n
m mn dx x x ψψδ=?
'
')''()'
',()'''('dx x x x i x F x x F x x -??
--?=∧
δδ )'()'
,'(x x x i x F -??
-=∧
δ
dx
x x
i x F x F p p p p )(),()('
'ψψ
??
-?=∧* 坐标表象的波函数 ()
,x t ψ给出t 时刻到粒子处于
()2
,x t dx ψ~x x dx +之间的几率
(),x t ψ满足Schrodinger
设上述定态方程的解为
()()
,,1,2,......n n x E n ψ=
()()
/
,n iE t n n n
x t C e
x ψψ-=∑
C n
为迭加常数，由初始条件决定。
动量表示 (
)/
1
ipx p
x e
ψ
=
)(x p
ψ构成正交完备集，体系的波函数),(t x ψ可以用 )(x p
ψ
展开，即
()()()
*,,p
p t dx x t x ?ψψ
=?
则含时Schrodinger 方程的一般解为
若
()()
,0x t x ψ?==则
()()
*n n
C dx x x ψ
?=?动量算符
p i
x
?
=-?其相应的本征态为P,本征函数为
两边同乘
()
*'
p dx x ψ?()()()()()
**'
'
,,p p
p dx x t x dx dp p t x x ψψ?ψψ=???()()()()
()
*'
,,'',p p
dp p t dx x dp p t p p p t ?ψψ?δ?==-=???
量子力学中几种表象及其之间的关系 摘要 体系的态可以用以坐标为变量的波函数ψ(x,t)来描写，力学量则以作用在这种波函数上的算符（量子力学中的算符代表对波函数的一种运算）来表示，这是量子力学中态和力学量的一种具体表述方式。态还可以用其他变量的函数作为波函数来描写体系的状态。 微观粒子体系的状态（量子态）和力学量的具体表示形式称为表象。 常用的表象有坐标表象、动量表象和能量表象。 而研究量子力学规律的各种表示形式以及这些不同形式之间的变换的理论，则称为表象理论。 关键词 态的表象 坐标表象 动量表象 Q 表象 算符表象 角动量表象 正文 体系的态既可用以x （表示全部坐标变量）为变量的波函数ψ(x,t)来描写，也可用以动量p 为变量的波函数c(p,t)来描写。ψ(x,t)和c(p,t)之间的变换关系是 式中 是动量的本征函数， dx x t x t p c dp x t p c t x p p )(),(),()(),(),(*ψ?=?=ψψψ /2 /1)2(1)(ipx p e x -=πψ
称ψ(x,t)是在坐标表象中的波函数，而c(p,t)是同一态在动量表象中的波函数。 由ψ(x,t)可知，粒子坐标在x 到x+dx 之间的概率 c 由(p,t ）可知，粒子动量在p 到p+dp 之间的概率 如果ψ(x,t)所描写的状态是具有动量p ’的自由粒子的状态，即ψ(x,t)=ψp ’(x,t),则 在动量表象中，粒子具有确定动量p ’的波函数是以动量p 为变量的δ函数。 那么，态在任意力学量Q 的表象中的描写方式又是什么样呢？ 设力学量Q 具有分立的本征值Q1,Q2,…Qn …，对应的本征函数为u1(x),u2(x),…,un(x),…,并组成正交归一的完全系。将态在坐标表象中的波函数ψ(x,t)按{un(x)}展开成 dx t x dx t x w 2 ),(),(ψ=dp t p c dp t p w 2 ),(),(=dx e x x dx x t x t p c t iEp p p p p /''')()()(),(),(-**?=ψ?=ψψψ /')'(t iEp e p p --=δ) ()(),(x u t a t x n n n ∑=ψ
1. 你认为Bohr 的量子理论有哪些成功之处？有哪些不成功的地方？试举一例说明。 (简述波尔的原子理论，为什么说玻尔的原子理论是半经典半量子的？) 答：Bohr 理论中核心的思想有两条：一是原子具有能量不连续的定态的概念；二是两个定态之间的量子跃迁的概念及频率条件。首先，Bohr 的量子理论虽然能成功的说明氢原子光谱的规律性，但对于复杂原子光谱，甚至对于氦原子光谱，Bohr 理论就遇到了极大的困难（这里有些困难是人们尚未认识到电子的自旋问题），对于光谱学中的谱线的相对强度这个问题，在Bohr 理论中虽然借助于对应原理得到了一些有价值的结果，但不能提供系统解决它的办法；其次，Bohr 理论只能处理简单的周期运动，而不能处理非束缚态问题，例如：散射；再其次，从理论体系上来看，Bohr 理论提出的原子能量不连续概念和角动量量子化条件等，与经典力学不相容的，多少带有人为的性质，并未从根本上解决不连续性的本质。 2. 什么是光电效应？光电效应有什么规律？爱因斯坦是如何解释光电效应的？ 答：当一定频率的光照射到金属上时，有大量电子从金属表面逸出的现象称为光电效应；光电效应的规律：a.对于一定的金属材料做成的电极，有一个确定的临界频率0υ，当照射光频率0υυ<时，无论光的强度有多大，不会观测到光电子从电极上逸出；b.每个光电子的能量只与照射光的频率有关，而与光强无关；c.当入射光频率0υυ>时，不管光多微弱，只要光一照，几乎立刻910s -≈观测到光电子。爱因斯坦认为：(1)电磁波能量被集中在光子身上，而不是象波那样散布在空间中，所以电子可以集中地、一次性地吸收光子能量，所以对应弛豫时间应很短，是瞬间完 成的。(2)所有同频率光子具有相同能量，光强则对应于光子的数目，光强越大，光子数目越多，所以遏止电压与光强无关，饱和电流与光强成正比。(3)光子能量与其频率成正比，频率越高，对应光子能量越大，所以光电效应也容易发生，光子能量小于逸出功时，则无法激发光电子。 3．简述量子力学中的态叠加原理，它反映了什么？ 答：对于一般情况，如果1ψ和2ψ是体系的可能状态，那么它们的线性叠加：1122c c ψψψ=+（12c c ，是复数）也是这个体系的一个可能状态。这就是量子力学中的态叠加原理。态叠加原理的含义表示当粒子处于态1ψ和2ψ的线性叠加态ψ时，粒子是既处于态1ψ，又处于态2ψ。它反映了微观粒子的波粒二象性矛盾的统一。量子力学中这种态的叠加导致在叠加态下观测结果的不确定性。 4. 什么是定态？定态有什么性质？ 答：体系处于某个波函数()()[]exp r t r iEt ψψ=-，所描写的状态时，能量具有确定值。这种状态称为定态。定态的性质：（1）粒子在空间中的概率密度及概率流密度不随时间变化；（2）任何力学量（不显含时间）的平均值不随时间变化；（3）任何力学量（不显含时间）取各种可能测量值的概率分布也不随时间变化。 5. 简述力学量与力学量算符的关系？ 答：算符是指作用在一个波函数上得出另一个函数的运算符号。量子力学中采用算符来表示微观粒子的力学量。如果量子力学中的力学量F 在经典力学中有相应的力学量，则表示这个力学量的算符?F 由经典表示式F （r,p ）中将p 换为算符?p 而得出的，即：
量子力学：不平凡的诞生预示了不平凡的神奇 ——浅谈量子力学与量子思维 理学院物理系林功伟 量子力学自诞生以来，极大地推动了现代科学和技术的发展，已经深刻地改变了我们的生活方式。从电脑、电视、手机到核能、航天、生物技术，处处它都在大显身手，它已经把人类社会带入量子时代。但量子理论究竟带给了我们什么？这个问题，至今带给我们的仍只是无尽的想象。近年来，校长钱旭红院士，从改变思维的角度出发，在多种场合呼吁全社会要重视量子思维方式并加以运用，不久前又在“文汇科技沙龙”上，提议让“量子思维”尽早走入中小学课堂。那么，量子力学究竟是什么？ 量子力学的诞生是一段波澜壮阔的传奇。它的发展史是物理学乃至整个科学史上最为动人心魄的篇章之一。不平凡的诞生预示了不平凡的神奇。在量子世界中，处事原则处处与我们熟悉的牛顿力学主宰的世界截然不同。在我们熟悉的世界，要么是波，要么是粒子。在量子世界，既是波也是粒子，既不是波也不是粒子，兼具波和粒子的特质，即波粒二象性。从而引申出量子叠加、测量塌缩、量子纠缠等种种神奇的现象。 量子叠加：鱼和熊掌亦可得兼 在经典的牛顿力学体系中，把粒子的运动都归结为确定轨道的机械运动。知道粒子某个时刻的运动状态与力的作用，就可以推断粒子的过去，也可以预知粒子的未来。就像一个算命先生，你告诉他生辰八字，他掐指一算就知道你的前世来生。在这种机械观下，仿佛一切都是注定的、唯一确定的。然而，在量子世界，一切都变得不一样。比如，有一天要从上海去北京，异想天开的你既想乘坐京沪高铁体验沿途的风光，又想搭乘飞机享受鸟瞰大地的感觉。我们习惯的方式是同
一时间我们只能选择其一，必须割爱其一。但在量子世界中你可以在火车上和飞机里共存量子叠加态上，鱼和熊掌亦可得兼。 这种量子叠加状态非常奇特。同一时刻，你既体验着高铁沿途的风光，也享受着飞机上鸟瞰大地的感觉，如果说同一时刻有两件事，但分别要求在火车上和在飞机里完成，量子叠加态的你完全可以神奇地一一照做。就像《西游记》中的孙悟空有分身术，同时一个上天一个入地。现在科学家们正利用这一原理来研制未来的量子计算机。量子计算机中的量子比特可以在无数的空间中量子叠加。它们并行地操作完成复杂的计算。已有研究表明这种量子并行计算确实可以在某些特定的复杂计算问题上大大提高效率。例如：一个400位的阿拉伯数字进行质数因子分解，目前即使最快的超级计算机也要耗时上百亿年，这几乎等于宇宙的整个寿命；而具有相同时钟脉冲速度的量子计算机可能只需要几分钟。还有利用量子快速搜索算法，可能很快从一个大森林里找到一片叶子，或者在一个沙滩上找到一颗沙子。在量子世界，“大海捞针”已不再是没有可能的事，简直“易如反掌”。 量子叠加不仅可以是同一个物质在它不同状态的叠加，还允许不同物质的叠加，哪怕这两个物质是迥然不同类的。比如光和原子，前者是宇宙中最快的，一眨眼可以绕地球好几周；后者可以慢悠悠地停留在某处。如果让它们量子叠加一起会怎么样呢？有种叫电磁诱导透明的技术就可以让光和原子相干叠加。叠加后我们称之为暗态极子，它是半光半原子的混合体，就像希腊神话中半人半神的帕尔修斯，既具备人的情感，也具备神的能力。人们发现这种半光半原子混合体的速度是介于之间的，它既不像光速那么快，也不像原子慢悠悠停留在某处，它的速度取决于光在其中叠加的比重。人们通过调节这个比重就可以让光乖乖地慢下来，需要的时候还可以让光再飞奔起来。在运用上，光子相互作用很小，而原子之间容易产生大的相互作用。有趣的是：最近，我们研究小组通过合理设计可以利用原子的优点来弥补光子的缺点，设计出强的单光子相互作用。如果把这个过程提升到量子思维的话，不就是我们生活中的“取长补短”“协同合作”吗？而这个思维能力正是当代社会所迫切需要的。
简述建立量子力学基本原理的思想方法 摘要：量子力学是大学物理专业的一门必修理论基础课程，它研究的对象是分子、原子和基本粒子。本文对建立量子力学基本原理的思想方法作一简单叙述，供学员在学习掌握量子力学的基本理论和方法时参考。 关键词：量子力学；力学量；电子；函数 作者简介 0引言 19世纪末，由于科学技术的发展，人们从宏观世界进入到微观领域，发现了一系列经典理论无法解释的现象，比较突出的是黑体辐射、光电效应和原子线光谱。普朗克于1900年引进量子概念后，上述问题才开始得到解决。爱凶斯坦提出了光具有微粒性，从而成功地解释了光电效应。 1量子力学 量子力学是研究微观粒子的运动规律的物理学分支学科，它主要研究原子、分子、凝聚态物质，以及原子核和基本粒子的结构、性质的基础理论，它与相对论一起构成了现代物理学的理论基础。量子力学不仅是近代物理学的基础理论之一，而且在化学等有关学科和许多近代技术中也得到了广泛的应用。 2玻尔的两条假设 玻尔在前人工作的基础上提出了两条假设，成功地解释了氢原子光谱，但对稍微复杂的原予(如氦原子)就无能为力。直到1924年德布罗意提出了微观粒子具有波粒二象性之后才得到完整解释。 1924年，德布罗意在普朗克和爱因斯坦假设的基础上提出了微观粒子具有波粒二象性的假设，即德布罗意关系。1927年，戴维孙和革末将电子作用于镍单晶，得到了与x射线相同的衍射现象，从而圆满地说明了电子具有波动性。 2.1自由粒子的波动性和粒子性 它的运动是最简单的一种运动，它充分地反映了自由粒子的波动性和粒子性，将波(平面波)粒( p，E) 二象性统一在其中。如果粒子不是自由的，而是在一个变化的力场中运动，德布罗意波则不能描写。我们将用一个能够充分反映二象性特点的
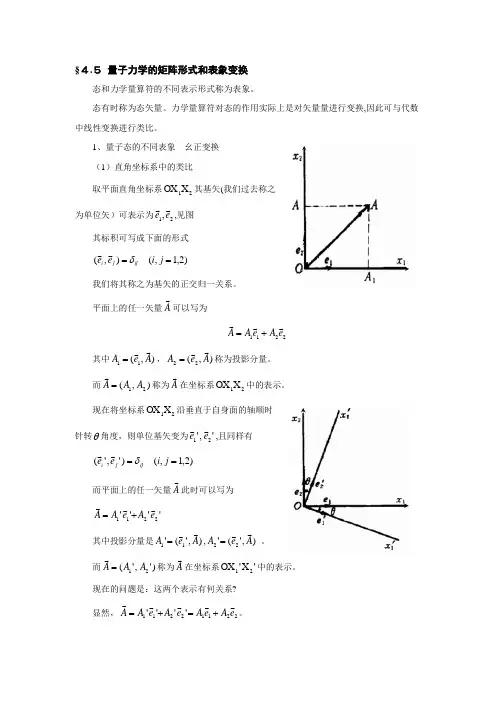
§4.5 量子力学的矩阵形式和表象变换 态和力学量算符的不同表示形式称为表象。 态有时称为态矢量。力学量算符对态的作用实际上是对矢量量进行变换，因此可与代数中线性变换进行类比。 1、量子态的不同表象 幺正变换 （1）直角坐标系中的类比 取平面直角坐标系21X OX 其基矢（我们过去称之为单位矢）可表示为21,e e ,见图 其标积可写成下面的形式 )2,1,(),(==j i e e ij j i δ 我们将其称之为基矢的正交归一关系。 平面上的任一矢量A 可以写为 2211e A e A A += 其中),(11A e A =，),(22A e A =称为投影分量。 而),(21A A A = 称为A 在坐标系21X OX 中的表示。 现在将坐标系21X OX 沿垂直于自身面的轴顺时针转θ角度，则单位基矢变为','21e e ，且同样有 )2,1,()','(==j i e e ij j i δ 而平面上的任一矢量A 此时可以写为 ''''2211e A e A A += 其中投影分量是),'('11A e A =，),'('22A e A =。 而)','(21A A A = 称为A 在坐标系'X 'OX 21中的表示。 现在的问题是：这两个表示有何关系？ 显然，22112211''''e A e A e A e A A +=+=。
用'1e 、'2e 分别与上式中的后一等式点积（即作标积），有 ),'(),'('2121111e e A e e A A += ),'(),'('2221212e e A e e A A += 表成矩阵的形式为 ??? ? ?????? ??=???? ??212212211121),'(),'(),'(),'(''A A e e e e e e e e A A 由于'1e 、1e 及'2e 、2e 的夹角为θ，显然有 ??? ? ?????? ??-=??? ? ?????? ??=???? ??21212212211121cos sin sin cos ),'(),'(),'(),'(''A A A A e e e e e e e e A A θθθθ 或记为 ??? ? ??=???? ??2121)(''A A R A A θ 其中 ??? ? ? ?-=θθ θθθcos sin sin cos )(R 是把A 在两坐标中的表示???? ??''21A A 和??? ? ??21A A 联系起来的变换矩阵。 变换矩阵的矩阵元正是两坐标系基矢间的标积，它表示基矢之间的关系。故R 给定，任何矢量在两坐标系间的关系也确定。 很容易证明，R 具有下述性质： I R R R R ==~ ~ 由于1)(det )~ det(2==R R R , 其中 321321)1()det(p p p t R R R R -∑=， 故称这种矩阵为正交矩阵。 但1det =R （对应于真转动（proper rotation ））且R R =* （实矩阵）
量子力学原理及其应用 师燕光电8班2012059080029 量子力学是近代自然科学的最重要的成就之一.在量子力学的世界里，一个 量子微观体系的状态是由一个波函数来描述的,而非由粒子的位置和动量描述， 这就是它与经典力学最根本的区别。这是被爱因斯坦和玻尔用“上帝跟宇宙玩掷骰子”来形容的学科，也是研究“极度微观领域物质”的物理学分支，它带来了许许多多令人震惊不已的结论——例如科学家们发现，电子的行为同时带有波和粒子的双重特征（波粒二象性），但仅仅是加入了人类的观察活动，就足以立刻改变它们的特性；此外还有相隔千里的粒子可以瞬间联系（量子纠缠）：不确定的光子可以同时去向两个方向（海森堡测不准原理）；更别提那只理论假设的猫既死了又活着（薛定谔的猫）?? 诸如以上，这些研究结果往往是颠覆性的，因为它们基本与人们习惯的逻辑思维相违背。以至于爱因斯坦不得不感叹道：“量子力学越是取得成功，它自身就越显得荒诞。” 直到现在，与一个世纪之前人类刚刚涉足量子领域的时候相比，爱因斯坦的观点似乎得到了更为广泛的共鸣。量子力学越是在数理上不断得到完美评分，就越显得我们的本能直觉竟是如此粗陋不堪。人们不得不承认，虽然它依然看起来奇异而陌生，但量子力学在过去的一百年里，已经为人类带来了太多革命性的发明创造。正像詹姆斯·卡卡廖斯在《量子力学的奇妙故事》一书引言中的所述：“量子力学在哪？你不正沉浸于其中吗。” 一、量子计算机 量子力学的海森堡测不准原理决定了粒子的位置和动量是不能同时确定的( )。当计算机芯片的密度很大时（即很小）将导致很大, 电子不再被束缚, 产生 量子干涉效应，而这种干涉效应会完全破坏芯片的功能。为了克服量子力学对计算机发展的限制,计算机的发展方向必然和量子力学相结合，这样不仅可以越过 量子力学的障碍,而且可以开辟新的方向。量子计算机就是以量子力学原理直接 进行计算的计算机.保罗·贝尼奥夫在1981 年第一次提出了制造量子计算机的理论。量子计算机的存储和读写头都以量子态存在的，这意味着存储符号可以是0、1 以及它们的叠加。 近年来的种种试验表明，量子计算机的计算和分析能力都超越了经典计算机。它具有如此优越的性质正在于它的存储读取方式量子化。对量子计算机的原理分析可知，以下两个个特性是令量子计算机优越性的根源所在：存储量大，速度高；可以实现量子平行态。 随着现代科学技术的发展，量子计算机也会逐渐走向现实研制和现实运用。量子计算机不但于未来的计算机产业的发展紧密相关,更重要的是它与国家的保密、电子银行、军事和通讯等重要领域密切相关。实现量子计算机是21 世纪科学技术的最重要的目标之一。 二、晶体管 美国《探索》杂志在线版给出的真实世界中量子力学的一大应用，就是人们早已不陌生的晶体管。1945 年的秋天，美国军方成功地制造出世界上第一台真空管计算机ENIAC。据当时的记载，这台庞然大物总重量超过30 吨，占地面积接近一个小型住宅，总花费高达100 万美元。如此巨额的投入，注定了真空管这种
量子力学基础简答题 1、简述波函数的统计解释； 2、对“轨道”和“电子云”的概念，量子力学的解释是什么？ 3、力学量G ?在自身表象中的矩阵表示有何特点？ 4、简述能量的测不准关系； 5、电子在位置和自旋z S ?表象下，波函数??? ? ??=ψ),,(),,(21z y x z y x ψψ如何归一化？解释各项的几率意义。 6、何为束缚态？ 7、当体系处于归一化波函数ψ(,) r t 所描述的状态时，简述在 ψ(,) r t 状态中测量力学量F 的可能值及其几率的方法。 8、设粒子在位置表象中处于态),(t r ψ,采用Dirac 符号时，若将ψ(,) r t 改写为ψ(,) r t 有何 不妥？采用Dirac 符号时，位置表象中的波函数应如何表示？ 9、简述定态微扰理论。 10、Stern —Gerlach 实验证实了什么？ 11、一个物理体系存在束缚态的条件是什么？ 12、两个对易的力学量是否一定同时确定？为什么？ 13、测不准关系是否与表象有关？ 14、在简并定态微扰论中，如 () H 0的某一能级) 0(n E ，对应f 个正交归一本征函数i φ（i =1，2，…， f ），为什么一般地i φ不能直接作为()H H H '+=???0的零级近似波函数？ 15、在自旋态χ1 2 ()s z 中， S x 和 S y 的测不准关系( )( )??S S x y 22?是多少？ 16、在定态问题中，不同能量所对应的态的迭加是否为定态Schrodinger 方程的解？同一能量 对应的各简并态的迭加是否仍为定态Schrodinger 方程的解？ 17、两个不对易的算符所表示的力学量是否一定不能同时确定？举例说明。 18说明厄米矩阵的对角元素是实的，关于对角线对称的元素互相共轭。 19何谓选择定则。 20、能否由Schrodinger 方程直接导出自旋？ 21、叙述量子力学的态迭加原理。 22、厄米算符是如何定义的？ 23、据[a ?，+ a ?]=1，a a N ???+=，n n n N =?，证明：1 ?-=n n n a 。 24、非简并定态微扰论的计算公式是什么？写出其适用条件。
量子力学教案 主讲周宙安 《量子力学》课程主要教材及参考书 1、教材： 周世勋，《量子力学教程》，高教出版社，1979 2、主要参考书： [1] 钱伯初，《量子力学》，电子工业出版社，1993 [2] 曾谨言，《量子力学》卷I，第三版，科学出版社，2000 [3] 曾谨言，《量子力学导论》，科学出版社，2003 [4] 钱伯初，《量子力学基本原理及计算方法》，甘肃人民出版社，1984 [5] 咯兴林，《高等量子力学》，高教出版社，1999 [6] L. I.希夫，《量子力学》，人民教育出版社 [7] 钱伯初、曾谨言，《量子力学习题精选与剖析》，上、下册，第二版，科学出版社，1999 [8] 曾谨言、钱伯初，《量子力学专题分析（上）》，高教出版社，1990 [9] 曾谨言，《量子力学专题分析（下）》，高教出版社，1999 [10] P.A.M.Dirac,The Principles of Quantum Mechanics (4th edition), Oxford University Press (Clarendon),Oxford,England,1958；（《量子力学原理》，科学出版社中译本，1979） [11]https://www.doczj.com/doc/078468166.html,ndau and E.M.Lifshitz, Quantum Mechanics (Nonrelativistic Theory) (2nd edition),Addison-Wesley,Reading,Mass,1965；（《非相对论量子力学》，人民教育出版社中译本，1980）
第一章绪论 量子力学的研究对象： 量子力学是研究微观粒子运动规律的一种基本理论。它是上个世纪二十年代在总结大量实验事实和旧量子论的基础上建立起来的。它不仅在进到物理学中占有及其重要的位置，而且还被广泛地应用到化学、电子学、计算机、天体物理等其他资料。 §1.1经典物理学的困难 一、经典物理学是“最终理论”吗？ 十九世纪末期，物理学理论在当时看来已经发展到相当完善的阶段。那时，一般物理现象都可以从相应的理论中得到说明： 机械运动（v< 第五章 量子力学的表象与表示 §5.1 幺正变换和反幺正变换 1, 幺正算符定义 对任意两个波函数)(r ?、)(r ψ，定义内积 r d r r )()(),(ψ?ψ?*?= (5.1) 按第一章中所说，(5.1)式的含义是：当微观粒子处在状态()r ψ时，找 到粒子处在状态()r ?的概率幅。 依据内积概念，可以定义幺正算符如下： “对任意两个波函数?、ψ，如果算符 U 恒使下式成立 ),()?,?(ψ?ψ?=U U (5.2) 而且有逆算符1?-U 存在，使得I U U U U ==--11????1，称这个算符U ?为幺正算符。” 任一算符A ?的厄米算符+A ?定义为：+A ?在任意?、ψ中的矩阵元恒由下式右方决定 ??(,)(,)A A ?ψ?ψ+= (5.3) 由此，幺正算符U ?有另一个等价的定义： “算符U ?为幺正算符的充要条件是 I U U U U ==++???? (5.4a) 或者说 1??-+=U U 。” (5.4b) 证明：若),()?,?(ψ?ψ?=U U 成立，则按+U ?定义， ),??()?,?(),(ψ?ψ?ψ?U U U U +== 由于?、ψ任意，所以 I U U =+?? 又因为U ?有唯一的逆算符1?-U 存在，对上式右乘以1?U -，即得 1??U U +-= 这就从第一种定义导出了第二种定义。类似，也能从第二种定义导出第一种定义。从而，幺正算符的这两种定义是等价的。 2, 幺正算符的性质 幺正算符有如下几条性质： i, 幺正算符的逆算符是幺正算符 证明：设 1-+=U U ， 则()()(),1 11--+++-===U U U U 所以1-U 也是幺正 1 这里强调了 U -1 既是对 U 右乘的逆又是对 U 左乘的逆。和有限维空间情况不同，无限维空间情况下，任一算符 U 有逆算符的三种情况：1）有一个左逆算符和无穷多个右逆算符；2）有一个右逆算符和无穷多个左逆算符；3）有一个左逆算符和一个右逆算符，并且它俩相等，唯有此时可简单地写为 U -1 。 第20卷 第2期太原教育学院学报V o l.20N o.2 2002年6月JOURNAL OF TA I YUAN INSTITUTE OF EDUCATI ON Jun.2002如何看待《原子物理学》中的 玻尔理论与量子力学 赵秀琴1, 贺兴建2 (1.太原师范学院,山西太原030031;2.太原市教育学院,山西太原030001) 摘 要:《原子物理学》在物理学的教育和学习中有着特殊的地位,特别是量子论建立初期的知识体系,是物理学获得知识、组织知识和运用知识的典范,通过量子论建立过程的物 理定律、公式后面的思想和方法的教学,使学生在原子物理的学习过程中掌握物理学的思想 和方法。 关键词:原子物理学;玻尔理论;量子力学 中图分类号:O562 文献标识码:A 文章编号:100828601(2002)022******* 《原子物理学》在物理学的教育和学习中有着特殊的地位,特别是量子论建立的初期知识体系,是物理学获得知识、组织知识和运用知识的典范,通过不断地提出经典物理无法解决的问题,提出假设、建立模型来解释并提出新的结论和预言,再用新的实验检验、修改或推翻,让学生掌握这种常规物理学的发展模式和过程。通过量子论的建立过程的物理定律、公式后面的思想和方法的教学,使学生在原子物理的学习过程中掌握物理学(特别是近代物理学)的思想和方法。 一、玻尔理论的创立 19世纪末到20世纪初,物理学的观察和实验已开始深入到物质的微观领域。在解释某些物理现象,如黑体辐射、光电效应、原子光谱、固体比热等时,经典物理概念遇到了困难,出现了危机。为了克服经典概念的局限性,人们被迫在经典概念的基础上引入与经典概念完全不同的量子化概念,从而部分地解决了所面临的困难。最先是由普朗克引入了对连续的经典力学量进行特设量子化假设。玻尔引入了原子定态概念与角动量量子化规则取得了很大的成果,预言了未激发原子的大小,对它的数量级作出了正确的预言。它给出了氢原子辐射的已知全部谱线的公式,它与概括了发射谱线实验事实的经验公式完全一致。同时,它还包括那些在建立理论时尚未知的谱线,它用几个物理量解释了里德伯经验常数。它向我们提供了一个形象化的系统(尽管有点冒险),并且对与发射有关的事件建立了一种物理秩序。玻尔模型把量子理论推广到原子上,一方面给普朗克的原子能量量子化的思想提供了物理根据,另一方面也解决了经典物理学回答不了的电子轨道的稳定性问题。 收稿日期:2001206212 作者简介:赵秀琴(1966-),女,山西太原人,太原师范学院讲师,教育学硕士。 量子力学和经典力学的区别与联系 量子力学和经典力学在的区别与联系 摘要 量子力学是反映微观粒子结构及其运动规律的科学。它的出现使物理学发生了巨大变革，一方面使人们对物质的运动有了进一步的认识，另一方面使人们认识到物理理论不是绝对的，而是相对的，有一定局限性。经典力学描述宏观物质形态的运动规律，而量子力学则描述微观物质形态的运动规律，他们之间有质的区别，又有密切联系。本文试图通过解释、比较，找出它们之间的不同，进一步深入了解量子力学，更好的理解和掌握量子力学的概念和原理。 经过量子力学与经典力学的对比我们可以发现，量子世界真正的基本特性：如果系统真的从状态A跳跃到B的话，那么我们对着其中的过程一无所知。当我们进行观察的时候，我们所获得的结果是有限的，而当我们没有观察的时候系统正在做什么，我们都不知道。量子理论可以说是一门反映微观运动客观规律的学说。经典物理与量子物理的最根本区别就是：在经典物理中，运动状态描述的特点为状态量都是一些实验可以测量得的，即在理论上这些量是描述运动状态的工具，实际上它们又是实验直接可测量的量，并可以通过测量这些状态量来直接验证理论。在量子力学中，微观粒子的运动状态由波函数描述，一切都是不确定的。但是当微观粒子积累到一定量是，它们又显现出经典力学的规律。 关键字：量子力学及经典力学基本内容及理论量子力学及经典力学的区别与联系 三、目录 摘要............................................................ ............ ... ... ...... (1) 关键字.................................................................. ...... ... ... ...... (1) 正文..................................................................... ...... ... ... ...... (3) 一、量子力学及经典力学基本内容及理论...... ............ ... ............ ...... ... (3) 经典力学基本内容及理论........................... ...... ......... ...... (3) 量子力学的基本内容及相关理论.................................... ...... (3) 二、量子力学及经典力学在表述上的区别与联系.................. ...... ... ...... (4) 河 北 大 学 课 程 考 核 试 卷 — 学年第 学期 级 专业（类） 考核科目 量子力学 课程类别 必修课 考核类型 考试 考核方式 闭卷 卷别 A （注：考生务必将答案写在答题纸上，写在本试卷上的无效） 一、概念题：（共20分，每小题4分） 1、简述波函数的统计解释； 2、对“轨道”和“电子云”的概念，量子力学的解释是什么？ 3、力学量G ?在自身表象中的矩阵表示有何特点？ 4、简述能量的测不准关系； 5、电子在位置和自旋z S ?表象下，波函数??? ? ??=ψ),,(),,(21z y x z y x ψψ如何归一化？解释 各项的几率意义。 二（20分）设一粒子在一维势场c bx ax x U ++=2)(中运动（0>a ）。求其定态能级和波函数。 三（20分）设某时刻，粒子处在状态)cos (sin )(212kx kx B x +=ψ，求此时粒子的平均动量和平均动能。 四（20分）某体系存在一个三度简并能级，即E E E E ===)0(3)0(2 )0(1。在不含时微扰H '?作用下，总哈密顿算符H ?在)0(?H 表象下为????? ? ?=**2110 0E E E H βαβα。求 受微扰后的能量至一级。 五（20分）对电子，求在x S ?表象下的x S ?、y S ?、z S ?的矩阵表示。 A —1—1 河 北 大 学 课 程 考 核 试 卷 — 学年第 学期 级 专业（类） 考核科目 量子力学 课程类别 必修课 考核类型 考试 考核方式 闭卷 卷别 B （注：考生务必将答案写在答题纸上，写在本试卷上的无效） 一、概念题：（共20分，每小题4分） 第三章一维定态问题 第三章 目 录 §3.1一般性质 (2) （1）定理1：一维运动的分立能级（束缚态），一般是不简 并的 ...................................... 2 （2）不同的分立能级的波函数是正交的。 .......... 4 （3）振荡定理 .................................. 4 （4）在无穷大位势处的边条件 .................... 5 §3.2阶梯位势 ....................................... 6 §3.3位垒穿透 (8) （1） E 量子力学习题（三年级用） 北京大学物理学院 二O O三年 第一章 绪论 1、计算下列情况的Broglie d e -波长，指出那种情况要用量子力学处理： （1）能量为eV .0250的慢中子 () 克2410671-?=μ .n ；被铀吸收； （2）能量为a MeV 的5粒子穿过原子克2410646-?=μ.a ； （3）飞行速度为100米/秒，质量为40克的子弹。 2、两个光子在一定条件下可以转化为正、负电子对，如果两光子的能量相等，问要实现这种转化，光子的波长最大是多少？ 3、利用Broglie d e -关系，及园形轨道为各波长的整数倍，给出氢原子能量 可能值。 第二章 波函数与波动力学 1、设()() 为常数a Ae x x a 222 1 -= ? （1）求归一化常数 （2）.?p ?,x x == 2、求ikr ikr e r e r -=?=?1121和的几率流密度。 3、若() ,Be e A kx kx -+=? 求其几率流密度，你从结果中能得到什么样的结 论？（其中k 为实数） 4、一维运动的粒子处于 ()? ? ?<>=?λ-0 00x x Axe x x 的状态，其中,0>λ求归一化系数A 和粒子动量的几率分布函数。 5、证明：从单粒子的薛定谔方程得出的粒子的速度场是非旋的，即求证 0=?? 其中ρ= υ/j 6、一维自由运动粒子，在0=t 时，波函数为 ()()x ,x δ=?0 求： ?)t ,x (=?2 第三章 一维定态问题 1、粒子处于位场 ()00 0000 ??? ?≥?=V x V x V 中，求：E ＞0V 时的透射系数和反射系数（粒子由右向左运动） 2、一粒子在一维势场 ?? ???>∞≤≤<∞=0 000x a x x V ) x ( 中运动。 （1）求粒子的能级和对应的波函数； （2）若粒子处于)x (n ?态，证明：,/a x 2= ().n a x x ?? ? ??π-=-2222 6112 3、若在x 轴的有限区域，有一位势，在区域外的波函数为 如 D S A S B D S A S C 22211211+=+= 这即“出射”波和“入射”波之间的关系， 量子力学诠释问题（一） 作者：孙昌璞( 中国工程物理研究院研究生院北京北京计算科学研究中心) 1 引言：量子力学的二元结构和其发展的二元状态上世纪二十年代创立的量子力学奠定了 人类认识微观世界的科学基础，成功地解释和预言了各种相关物理效应。然而，关于波函数的意义，自爱因斯坦和玻尔旷世之争以来众说纷纭，并无共识。直到今天，量子力学发展还是处在这样一种二元状态。对此有人以玻尔的“互补性”或严肃或诙谐地调侃之，以“shut up and calculate”的工具主义观点处之以举重若轻。这样一个二元状态主要是由于附加在玻恩几率解释之上的“哥本哈根诠释”之独有的部分：外部经典世界存在是诠释量子力学所必需的，是它产生了不服从薛定谔方程幺正演化的波包塌缩，使得量子力学二元化了。今天，虽然波包塌缩概念广被争议，它导致的后选择“技术”却被广泛地应用于量子信息技术的各个方面，如线性光学量子计算和量子离物传态的某些实验演示。早年，薛定谔曾经写信严厉批评了当时的物理学家们，他在给玻恩的信中写到：“我确实需要给你彻底洗脑……你轻率地常常宣称哥本哈根解释实际上已经被普遍接受，毫无保留地这样宣称，甚至是在一群外行人面前——他们完全在你的掌握之中。这已经是道德底线了……你真的如此确信人类很快就 会屈从于你的愚蠢吗？”1979 年，Weinberg在《爱因斯坦的错误》一文中批评了玻尔对测量过程的不当处理：“量子经典诠释的玻尔版本有很大的瑕疵，其原因并非爱因斯坦所想象的。哥本哈根诠释试图描述观测(量子系统)所发生的状况，却经典地处理观察者与测量的过程。这种处理方法肯定不对：观察者与他们的仪器也得遵守同样的量子力学规则，正如宇宙的每一个量子系统都必须遵守量子力学规则。”“哥本哈根诠释可以解释量子系统的量子行为，但它并没有达成解释的任务，那就是应用波函数演化方程于观察者和他们的仪器。”最近温伯格又进一步强调了他对“标准”量子力学的种种不满。在量子信息领域，不少人不加甄别地使用哥本哈根诠释导致的“后选择”方案，其可靠性令人怀疑！其实，在量子力学幺正演化的框架内，多世界诠释不引入任何附加的假设，成功地描述了测量问题。由于隐变量理论在理论体系上超越了量子力学框架，本质上是比量子力学更基本的理论，所以本文对Bell 不等式不作系统讨论。自上世纪八十年代初，人们先后提出了各种形式迥异的量子力学新诠释，如退相干、自洽历史、粗粒化退相干历史和量子达尔文主义，但实际上都是多世界诠释的拓展和推广。2 哥本哈根诠释及其推论哥本哈根诠释的核心内容是“诠释量子世界，外部的经典世界必不可少”。波函数描述微观系统的状态，遵循态叠加原理，即：如果|?1> Dirac 符号系统与表象 一、Dirac 符号 1. 引言 我们知道任一力学量在不同表象中有不同形式，它们都是取定了某一具体的 力学量空间,即某一具体的力学量表象。量子描述除了使用具体表象外，也可以不取定表象，正如几何学和经典力学中也可用矢量形式 A 来表示一个矢量，而不用具体坐标系中的分量(A x , A y , A z )表示一样。 量子力学可以不涉及具体表象来讨论粒子的状态和运动规律。这种抽象的描 述方法是由 Dirac 首先引用的，本质是一个线性泛函空间，所以该方法所使用的符号称为 Dirac 符号。 2. 态矢量 （1）. 右矢空间 力学量本征态构成完备系，所以本征函数所对应的右矢空间中的右矢也组成该空间的完备右矢（或基组），即右矢空间中的完备的基本矢量（简称基矢）。 右矢空间的任一矢量 |ψ> 可按该空间的某一完备基矢展开。例如： =n n a n ψ∑ （2）. 左矢空间 右矢空间中的每一个右矢量在左矢空间都有一个相对应的左矢量，记为 < |。右矢空间和左矢空间称为伴空间或对偶空间，<ψ | 和 |ψ> 称为伴矢量。 的关系 |ψ >按 Q 的左基矢 |Q n > 展开： |ψ > = a 1 |Q 1> + a 2 |Q 2> + ... + a 3 |Q 3 > + ... 展开系数即相当于 Q 表象中的表示： 12 n a a a ψ?? ? ? ?= ? ? ?? ? <ψ| 按 Q 的左基矢 量子力学和经典力学在的区别与联系 摘要 量子力学是反映微观粒子结构及其运动规律的科学。它的出现使物理学发生了巨大变革，一方面使人们对物质的运动有了进一步的认识，另一方面使人们认识到物理理论不是绝对的，而是相对的，有一定局限性。经典力学描述宏观物质形态的运动规律，而量子力学则描述微观物质形态的运动规律，他们之间有质的区别，又有密切联系。本文试图通过解释、比较，找出它们之间的不同，进一步深入了解量子力学，更好的理解和掌握量子力学的概念和原理。 经过量子力学与经典力学的对比我们可以发现，量子世界真正的基本特性：如果系统真的从状态A跳跃到B的话，那么我们对着其中的过程一无所知。当我们进行观察的时候，我们所获得的结果是有限的，而当我们没有观察的时候系统正在做什么，我们都不知道。量子理论可以说是一门反映微观运动客观规律的学说。经典物理与量子物理的最根本区别就是：在经典物理中，运动状态描述的特点为状态量都是一些实验可以测量得的，即在理论上这些量是描述运动状态的工具，实际上它们又是实验直接可测量的量，并可以通过测量这些状态量来直接验证理论。在量子力学中，微观粒子的运动状态由波函数描述，一切都是不确定的。但是当微观粒子积累到一定量是，它们又显现出经典力学的规律。 关键字：量子力学及经典力学基本内容及理论量子力学及经典力学的区别与联系 目录 三、目录 摘要 (1) 关键字 (1) 正文 (3) 一、量子力学及经典力学基本内容及理论……………………………………………… 3 经典力学基本内容及理论 (3) 量子力学的基本内容及相关理论 (3) 二、量子力学及经典力学在表述上的区别与联系 (4) 微观粒子和宏观粒子的运动状态的描述 (4) 量子力学中微观粒子的波粒二象性 (5) 三、结论：量子力学与经典力学的一些区别对比 (5) 参考文献 (6)量子力学的表象与表示
如何看待《原子物理学》中的玻尔理论与量子力学
量子力学和经典力学的区别与联系(完整版)
量子力学习题
量子力学的矩阵形式及表象理论
量子力学的矩阵形式及表象理论
量子力学诠释问题(一)
量子力学之狄拉克符号系统与表象
和 <φ| 的标积为：*n n n b a ?ψ=∑。显然<φ|ψ>* = <ψ|φ>。对于满足归 一化条件的内积有：*1n n n a a ψψ= =∑。 这样，本征态的归一化条件可以写为：
量子力学和经典力学的区别与联系
相关主题
文本预览