WPS中用excel做正态分析

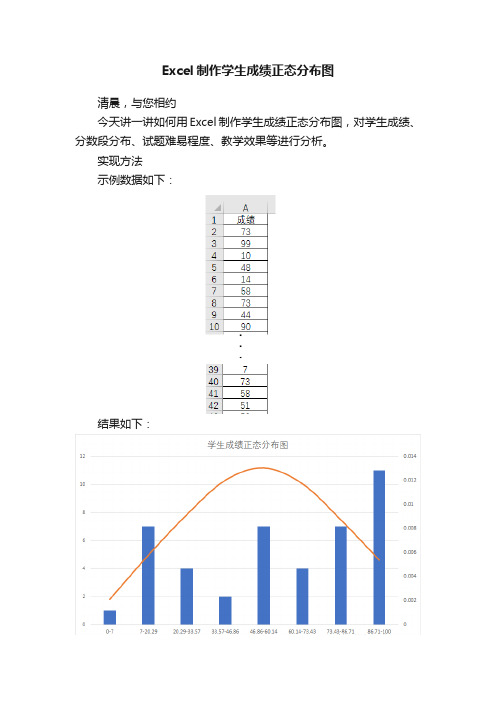
Excel制作学生成绩正态分布图清晨，与您相约今天讲一讲如何用Excel制作学生成绩正态分布图，对学生成绩、分数段分布、试题难易程度、教学效果等进行分析。

实现方法示例数据如下：结果如下：正态分布图中：1.成绩分数段直方图，显示各个分数段的人数；2.正态分布曲线的高峰位于平均成绩位置，由平均成绩所在处开始，分别向左右两侧逐渐均匀下降；3.直方图与曲线的对比分析，可以得到各种信息。

第一步：分析成绩对成绩进行分析，分析出最大值、最小值、极差（最大值—最小值）、成绩分段数量、分段间距。

下图是分析的结果及对应公式：第二步：确定分数段“分段点”就是确定直方图的横轴坐标起止范围和每个分数段的起止位置。

第一个分段点要小于等于最小成绩，然后依次加上“分段间距”，直到最后一个数据大于等于最高成绩为止。

实际分段数量可能与计算的“分段数”稍有一点差别。

如下图：第一个分段点7是手工输入，在第二个分段点H2处输入公式=H2+$D$6，往下填充，填出各个分段点。

第三步：计算段内人数选中I2:I9,输入公式：=FREQUENCY(A2:A44,H2:H9)，<Ctrl+Shift+Enter>三键结束，即可算出各分数段人数。

关于FREQUENCY函数，请参考：Excel108 | FREQUENCY函数分段计数）第四步：计算成绩正态分布值选中J2，输入公式：=NORMDIST(I2,AVERAGE($A$2:$A$44),STDEV($A$2:$A$44), 0)，确定并往下填充，即可得到每个成绩段的正态分布值，正态分布概率密度正态分布函数“NORMDIST”获取。

NORMDIST 函数：•返回指定平均值和标准偏差的正态分布函数语法：•NORMDIST(x,mean,standard_dev,cumulative)•NORMDIST 函数语法具有下列参数：•X 必需。

需要计算其分布的数值。

•Mean 必需。

分布的算术平均值。

excel画正态分布曲线图正态分布是一种被广泛应用的概率分布，它的概率密度函数是一个标准的钟形曲线，它的简称为NDF(Normal Distribution Function)，或者叫作正态分布曲线。

正态分布在做实验中经常使用，但人们不得不用许多繁琐的统计学公式来绘制出正态分布曲线。

为了使用更简便的方法来绘制正态分布曲线，本文将介绍如何使用微软的Excel构建正态分布曲线图。

首先，需要准备一份Excel表格，将某一维度的分布曲线数据记录在一列中。

这里以“height”（身高）为例，在第一列的表格中，列出人的身高（以厘米为单位），在第二列的表格中，记录身高的频数（以人数为单位）。

接下来，在Excel中选择插入“图表”，选择“线形图”，把第一列的数据作为图表的X轴，第二列的数据作为图表的Y轴。

然后，在图表右上角的菜单中，点击“选项”，勾选“折线”并且把它改为“曲线”，当把曲线拖动到正常位置时，图表就出来了。

最后，可以给正态分布曲线图添加标题和比例尺，使其更加易于理解。

正态分布曲线图主要用于表示一组数据的分布特征。

例如，可以用正态分布曲线图来表示全国人口的年龄分布情况，或是某类测试成绩的分布特征，或是市场消费行为的变化情况。

另外，正态分布曲线图也可以用于比较两个不同维度的数据分布特征，从而更好地表现出这些数据之间的相关性。

正态分布曲线图被广泛应用于商业决策分析、统计学、有限元素分析等领域中，可以帮助人们对数据的变化趋势进行更加客观的分析，从而准确地了解现象背后的规律性。

使用Excel绘制正态分布曲线图不但简单易操作，而且能够获得较为准确的曲线图，因此得到了广泛的应用。

以上就是本文关于如何使用Excel画正态分布曲线图的介绍，希望读者通过本文的介绍，能够对Excel构建正态分布曲线图有一个较为完整的了解，可以灵活运用Excel技术来解决一些数据处理问题。

Excel数据统计分析-专业分析-相关性分析（含正态分布图制作）1、准备基础数据，如下图所⽰：
我们要根据以上数据做出正态分布图，接着做相关性分析图，正态分布图我们知道是⼀个开⼝
向下的抛物线，中间的数据占整个数据的60%左右，所以我们需要对基础数据进⾏数据统计然
后根据统计的数据进⾏画图；
2、进⾏数据统计
进⾏数据统计时我们需要以下参数：
3、画图前数据准备
4、画图
基础数据出来了，画图也就⽔到渠成了，我们选择H1到K8的所有单元格，然后插⼊图表—创建
⾃定义组合图，次坐标轴选择正态分布图（带平滑曲线的散点图），然后编辑系列值等，并进
⾏图表美化后就可以了。

实现的效果图如下：
画相关性分析图我们可以直接选择b1到c38的所有数据插⼊带平滑曲线的散点图，然后设置⼀下
坐标轴的起始值就可以了。

效果如下：。

excel 正态分布曲线
Excel中如何绘制正态分布曲线？正态分布是一种重要的概率分布，广泛应用于统计学、金融学、经济学、医学等领域。

Excel 作为强大的数据处理工具，可以方便地绘制正态分布曲线。

首先，在Excel中输入数据，可以使用NORM.DIST函数计算随机变量X的概率密度函数值。

NORM.DIST函数的语法为：
NORM.DIST(x, mean, standard_dev, cumulative)，其中x表示要计算概率密度函数值的随机变量，mean表示随机变量X的均值，standard_dev表示随机变量X的标准差，cumulative表示是否计算累积分布函数值。

例如，在单元格A1中输入
=NORM.DIST(0,1,1,FALSE)，即可计算X=0处的概率密度函数值。

然后，在Excel中绘制正态分布曲线，可以使用折线图或散点图。

具体步骤如下：
1.将随机变量X的取值范围输入到Excel的一个列中，例如，在A列中输入-3,-
2.9,-2.8,...,2.8,2.9,3，表示X的取值范围为-3到3，步长为0.1。

2.在另一个列中输入随机变量X对应的概率密度函数值，例如，在B列中输入=NORM.DIST(A1,1,1,FALSE)，并将此公式复制到下面的单元格中，直到填满整个列。

3.选中A列和B列中的所有数据，点击插入菜单中的折线图或散点图，即可绘制出正态分布曲线。

4.可以根据需要对图表进行格式调整，例如，调整坐标轴范围
和标签，添加标题和图例等。

绘制正态分布曲线是Excel中常见的数据可视化任务之一，掌握这一技能可以帮助我们更好地理解和分析数据。

在Excel中创建正态分布图表时，并没有直接的“正态分布模板”，因为正态分布
图通常基于用户输入的数据参数（均值和标准差）来模拟或拟合正态分布曲线。

但你可以手动构建这样的图表，以下是简化的步骤：
1.计算正态分布函数值：
o使用Excel内置函数NORM.DIST(x, mean, standard_dev,
cumulative)来计算不同x值下的正态分布概率密度函数值。

其
中，
▪x是你想要计算分布概率的位置，
▪mean是正态分布的均值，
▪standard_dev是标准差，
▪cumulative如果是TRUE，则返回累积分布函数值，如果是
FALSE，则返回概率密度函数值。

2.生成数据系列：
o在Excel工作表中选择一列，输入一系列的x值（例如从-3到+3标准差范围内的等间距数值）。

o在相邻列中使用上述函数计算出对应的正态分布概率密度值。

3.绘制图表：
o选择包含x值和对应正态分布概率密度值的两列数据。

o在Excel中点击“插入”选项卡，然后选择“图表”>“散点图”或者“XY 散点图”类型。

o根据需要调整图表样式和标签，包括X轴标题（例如“变量
X”）、Y轴标题（例如“概率密度”）以及图表标题（例如“正态分
布曲线”）。

若你已经有了实际的数据并且想检查它们是否符合正态分布，可以计算数据的描述性统计量（如平均值、标准差），并利用直方图与理论正态曲线进行对
比，这可以通过Excel的数据分析工具包中的相关功能实现。

不过，展示一个理论上的正态分布曲线通常就是通过上述步骤来完成的。

excel有个数据分析工具，里面可以做直方图，但是正态分布图不能直接做。

若要两种图都显示，那么就需要用到函数了。

方法如下：
假若你的数据在A1:A10
1.统计数据个数；任意选个单元格，如B1，输入count(A1:A10)；
2.求最大值；如B2中输入：max(A1:A10)
3.求最小值；如B3中输入：min(A1:A10)
4.求平均值；如B4中输入：average(A1:A10)
5.求标准偏差：如B5中输入：stdev(A1:A10)
6.获得数据区间；用最大值减最小值；如B6中输入：B3-B2
7.获得直方图个数；个数的开放加1，如B7中输入：sqrt（B1）+1
8.获得直方图组距；用区间除以(直方图个数-1)，如B8中输入B7/(B7-1)
下面就开始作图了：
1.任选个空单元格：如C列第一个单元格C1，令C1等于最小值，即输入=B3
2.在C2中输入=C1+$B$8 (最小值逐渐累加，绝对引用)
3.选中C2，然后向下拉，直到数据大于最大值就可以了；比如你拉到C5了。

4.统计频数，如在D1中输入frequency（A1:A10，C1:C5）确定，然后将选中D1到D5，将光标定位到公式栏，同时按住ALT+Shift+Enter
5.统计正态分布的数据，E1中输入normdist（C1，$B$4,$B$5,0）回车；然后选中E1，下拉到E5
选择数据区域-二维堆积柱形图-确定完成，点击二维堆积柱形图的上数据图-右键-更改系列图标类型-选择折线图-图标空白处-右键-设置数据系列格式,看图吧：
-----
----
----
------
--。

正态分布函数的语法是NORMDIST(x，mean，standard_dev，cumulative)cumulative为一逻辑值，如果为0则是密度函数，如果为1则是累积分布函数。

如果画正态分布图，则为0。

例如均值10%，标准值为20%的正态分布，先在A1中敲入一个变量，假定－50，选中A列，点编辑－填充－序列，选择列，等差序列，步长值10，终止值70。

然后在B1中敲入NORMDIST （A1，10，20，0），返回值为0.000222，选中B1，当鼠标在右下角变成黑十字时，下拉至B13，选中A1B13区域，点击工具栏上的图表向导－散点图，选中第一排第二个图，点下一步，默认设置，下一步，标题自己写，网格线中的勾去掉，图例中的勾去掉，点下一步，完成。

图就初步完成了。

下面是微调把鼠标在图的坐标轴上点右键，选坐标轴格式，在刻度中填入你想要的最小值，最大值，主要刻度单位（x轴上的数值间隔），y轴交叉于（y 为0时，x多少）等等。

确定后，正态分布图就大功告成了。

PS：标准正态分布的语法为NORMSDIST(z)，正态分布（一）NORMDIST函数的数学基础利用Excel计算正态分布，可以使用函数。

格式如下：变量，均值，标准差，累积，其中：变量：为分布要计算的值；均值：分布的均值；标准差：分布的标准差；累积：若1，则为分布函数；若0，则为概率密度函数。

当均值为0，标准差为1时，正态分布函数即为标准正态分布函数。

例3已知考试成绩服从正态分布，，，求考试成绩低于500分的概率。

解在Excel中单击任意单元格，输入公式：“ 500，600，100，1 ”，得到的结果为0.158655，即，表示成绩低于500分者占总人数的15.8655%。

例4假设参加某次考试的考生共有2000人，考试科目为5门，现已知考生总分的算术平均值为360，标准差为40分，试估计总分在400分以上的学生人数。

假设5门成绩总分近似服从正态分布。

【EXCEL】用excel做频率和正态分布图2012-04-06 11:07:47来自: VeraTulips(I am what I saw)excel有个数据分析工具，里面可以做直方图，但是正态分布图不能直接做。

若要两种图都显示，那么就需要用到函数了。

方法如下：假若你的数据在A1:A101.统计数据个数；任意选个单元格，如B1，输入count(A1:A10)；2.求最大值；如B2中输入：max(A1:A10)3.求最小值；如B3中输入：min(A1:A10)4.求平均值；如B4中输入：average(A1:A10)5.求标准偏差：如B5中输入：stdev(A1:A10)6.获得数据区间；用最大值减最小值；如B6中输入：B3-B27.获得直方图个数；个数的开放加1，如B7中输入：sqrt（B1）+18.获得直方图组距；用区间除以(直方图个数-1)，如B8中输入B7/(B7-1)下面就开始作图了：1.任选个空单元格：如C列第一个单元格C1，令C1等于最小值，即输入=B32.在C2中输入=C1+$B$8 (最小值逐渐累加，绝对引用)3.选中C2，然后向下拉，直到数据大于最大值就可以了；比如你拉到C5了。

4.统计频数，如在D1中输入frequency（A1:A10，C1:C5）确定，然后将选中D1到D5，将光标定位到公式栏，同时按住ALT+Shift+Enter5.统计正态分布的数据，E1中输入normdist（C1，$B$4,$B$5,0）回车；然后选中E1，下拉到E5这样数据都准备好了，剩下来就直接作图了，那就不用说了吧视频讲解：/v_show/id_XMTM5ODIyMjAw.html这个非常好！！！喜欢用Excel的回归分析绘制[正态概率图]步骤步骤0：检查有无安装分析工具库工具>加载宏对话框中勾选[分析工具库]后确定步骤1：数据布署1将数据放到适当位置，例如表1有10个数据加上标志放到的[A1:A11]2紧接数据列旁加上一列，给予标志与1~10的数据列如表1所示← 此处为关键步骤步骤2：将准备好的二列数据进行回归分析以绘制[正态概率图]呼叫 [回归]工具>数据分析>回归在[回归]对话框中填入1 [Y值输入区域] B1:B112 [X值输入区域] A1:A113 勾选[标志]4 勾选[正态概率图]← 此处为关键5 請自訂[輸出選項]，點擊[確定]後即可得到迴歸分析的結果，如上表中的A圖6 调整回归结果的[正态概率图]大小方便使用用Excel的回归分析绘制[正态概率图]的补充说明1用Excel所作[正态概率图]与用Minitab所作的，二者图表的纵横坐标刚好颠倒、为方便初次使用者比较，笔者特别将A图纵横轴颠倒而画出B图，此时所用的画图数据是[回归]报表中的[百分比排位]与[Xdata]数列如表2所示，因笔者使用繁体版Excel所以可能标志上或许会有出入2用Excel或Minitab绘制[正态概率图]都使用『median rank』当作概率图的百分位数，但二者使用计算『median rank』的方法依据不同，所以『median rank』数据略有不同，但一般不会妨碍正态性的判断。

excel画正态分布曲线图Excel是微软公司出品的办公软件，使用非常广泛。

它不仅可以用来处理各种表格，还可以制作精美的图表。

本文将介绍如何使用Excel来画正态分布曲线图。

首先，我们需要准备一份数据表，该表应包含来自观测值的观测数据。

在Excel中，将数据表格式设置为“简单表格”，然后把数据复制到此表格中。

接下来，在新工作表中插入正态分布曲线图。

打开图表编辑器，点击“图表类型”，然后选择“曲线图”，点击“确定”。

接着，在“数据”标签中，选择“添加数据”，并将Excel中的数据表中的数据复制到此框中。

点击“确定”，曲线图就生成了。

接下来，我们就可以对正态分布曲线图进行美化了。

先把X轴的标题改成“观测值”，Y轴标题改成“概率”，然后把曲线的粗细调整一下，把颜色改成你喜欢的颜色，最后可以把图表的标题改成“正态分布图”，这样就可以得到一幅精美的正态分布图了。

正态分布图有很多用途，它可以帮助用户更好地分析和理解数据。

例如，我们可以使用正态分布图查看一组观测数据的分布规律。

我们可以看到，这些观测值有多少在平均值附近，有多少偏离平均值。

另外，正态分布图还可以用来评估观测数据是否符合正态分布，以及观测数据的变异情况。

最后，我们可以介绍一下使用Excel画正态分布曲线图的优势。

Excel是一款只需要很少的操作就可以搞定的软件，使用它画正态分布曲线图相当容易，而且能得到较高质量的曲线图，并且可以在图表中添加更多的新元素，比如说添加坐标轴的网格线、标题等等，让曲线图变得更为美观。

以上就是本文关于“Excel画正态分布曲线图”的内容，希望本文能够帮助读者学会如何使用Excel来制作正态分布曲线图，深入了解正态分布图的特点以及它的用途，也希望读者在制作这种图表时能够节省时间，得到更好的效果。

一、引言Excel作为一款功能强大的电子表格软件，不仅可以用于数据处理和分析，还可以用来生成各种统计图表。

其中，利用Excel生成正态分布曲线是许多统计分析工作中常见的应用之一。

本文将介绍如何利用Excel中的正态分布公式来生成正态分布曲线，以及如何在生成过程中进行参数设置和结果分析。

二、正态分布概述1. 什么是正态分布正态分布又称高斯分布，是概率论和统计学中最重要的连续型概率分布之一。

正态分布的概率密度函数呈钟型曲线，左右对称，最高点位于均值处，随着离均值的距离越远，密度越小。

正态分布在自然界和实际应用中广泛存在，因此在统计分析中具有重要的意义。

2. 正态分布的特点正态分布具有以下几个重要特点：（1）均值决定了正态分布曲线的位置；（2）标准差决定了正态分布曲线的宽窄；（3）正态分布呈对称的钟形曲线；（4）约68的数据落在均值加减一个标准差范围内，约95的数据落在均值加减两个标准差范围内。

三、Excel中的正态分布公式在Excel中，可以利用正态分布函数来生成正态分布曲线。

Excel的正态分布函数有两种，分别是NORM.DIST和NORM.INV。

NORM.DIST函数用于计算正态分布的概率密度函数值，而NORM.INV函数用于计算给定概率下的正态分布的值。

1. NORM.DIST函数NORM.DIST函数的语法为：=NORM.DIST(x,mean,standard_dev,cumulative)其中，x为要计算其概率密度函数值的数值；mean为正态分布的均值；standard_dev为正态分布的标准差；cumulative为一个逻辑值，用于指定计算累积概率密度函数值还是概率密度函数值。

2. NORM.INV函数NORM.INV函数的语法为：=NORM.INV(probability,mean,standard_dev)其中，probability为要计算其反函数值的概率值；mean和standard_dev分别为正态分布的均值和标准差。