正态分布图做法(输入数据自动生成)
- 格式:xls
- 大小:852.50 KB
- 文档页数:14


Excel中2010版进行绘制标准正态分布概率密度函数图的方
法
在社会经济学问题中,有许多随机变量的概率分布都服从正态分布。
今天,店铺就教大家在Excel中2010版进行绘制标准正态分布概率密度函数图的方法。
Excel中2010版进行绘制标准正态分布概率密度函数图的步骤先输入数据,这里是以初始值为”-2“,终值为”2“的等差数列,作为标准正态变量的值。
选中B1单元格,选择函数标签。
在选择类别中找到”统计“,选择”NORMDIST“,点击”确定“。
在X中输入A1,
在mean中输入0(这里是计算均值),
在stand_dev中输入1(标准差为1),
最后在Cumulative中输入0或false(表示计算的是概率密度)。
点击”确定“。
单击B1单元格,鼠标指向单元格右下角填充空点,往下拖。
然后选中区域,找到”插入“中的折线图,选择一个。
效果图如下。

excel拟合正态分布曲线
要在Excel中拟合正态分布曲线,可以按照以下步骤:
1. 输入数据:将正态分布的观测值按照从小到大的顺序排列,输入到Excel的工作表中。
2. 计算平均数和标准差:使用Excel的平均数和标准差函数(AVERAGE和STDEV)计算出样本的平均数和标准差。
3. 计算正态分布函数值:对于每个输入值,使用Excel的正态分布函数(NORM.DIST)计算出其对应的正态分布函数值。
4. 绘制曲线拟合图:将输入值和上一步计算出的正态分布函数值放入散点图中,并使用Excel的趋势线功能添加一条正态分布曲线。
5.调整曲线参数:根据实际情况,可以调整曲线的参数(如平均值和标准差)以更好地拟合数据。

python⽣成正态分布数据,并绘图和解析1、⽣成正态分布数据并绘制概率分布图import pandas as pdimport numpy as npimport matplotlib.pyplot as plt# 根据均值、标准差,求指定范围的正态分布概率值def normfun(x, mu, sigma):pdf = np.exp(-((x - mu)**2)/(2*sigma**2)) / (sigma * np.sqrt(2*np.pi))return pdf# result = np.random.randint(-65, 80, size=100) # 最⼩值,最⼤值,数量result = np.random.normal(15, 44, 100) # 均值为0.5,⽅差为1print(result)x = np.arange(min(result), max(result), 0.1)# 设定 y 轴,载⼊刚才的正态分布函数print(result.mean(), result.std())y = normfun(x, result.mean(), result.std())plt.plot(x, y) # 这⾥画出理论的正态分布概率曲线# 这⾥画出实际的参数概率与取值关系plt.hist(result, bins=10, rwidth=0.8, density=True) # bins个柱状图,宽度是rwidth(0~1),=1没有缝隙plt.title('distribution')plt.xlabel('temperature')plt.ylabel('probability')# 输出plt.show() # 最后图⽚的概率和不为1是因为正态分布是从负⽆穷到正⽆穷,这⾥指截取了数据最⼩值到最⼤值的分布根据范围⽣成正态分布:result = np.random.randint(-65, 80, size=100) # 最⼩值,最⼤值,数量根据均值、⽅差⽣成正态分布:result = np.random.normal(15, 44, 100) # 均值为0.5,⽅差为12、判断⼀个序列是否符合正态分布import numpy as npfrom scipy import statspts = 1000np.random.seed(28041990)a = np.random.normal(0, 1, size=pts) # ⽣成1个正态分布,均值为0,标准差为1,100个点b = np.random.normal(2, 1, size=pts) # ⽣成1个正态分布,均值为2,标准差为1, 100个点x = np.concatenate((a, b)) # 把两个正态分布连接起来,所以理论上变成了⾮正态分布序列k2, p = stats.normaltest(x)alpha = 1e-3print("p = {:g}".format(p))# 原假设:x是⼀个正态分布if p < alpha: # null hypothesis: x comes from a normal distributionprint("The null hypothesis can be rejected") # 原假设可被拒绝,即不是正态分布else:print("The null hypothesis cannot be rejected") # 原假设不可被拒绝,即使正态分布3、求置信区间、异常值import numpy as npimport matplotlib.pyplot as pltfrom scipy import statsimport pandas as pd# 求列表数据的异常点def get_outer_data(data_list):df = pd.DataFrame(data_list, columns=['value'])df = df.iloc[:, 0]# 计算下四分位数和上四分位Q1 = df.quantile(q=0.25)Q3 = df.quantile(q=0.75)# 基于1.5倍的四分位差计算上下须对应的值low_whisker = Q1 - 1.5 * (Q3 - Q1)up_whisker = Q3 + 1.5 * (Q3 - Q1)# 寻找异常点kk = df[(df > up_whisker) | (df < low_whisker)]data1 = pd.DataFrame({'id': kk.index, '异常值': kk})return data1N = 100result = np.random.normal(0, 1, N)# result = np.random.randint(-65, 80, size=N) # 最⼩值,最⼤值,数量mean, std = result.mean(), result.std(ddof=1) # 求均值和标准差# 计算置信区间,这⾥的0.9是置信⽔平conf_intveral = stats.norm.interval(0.9, loc=mean, scale=std) # 90%概率print('置信区间:', conf_intveral)x = np.arange(0, len(result), 1)# 求异常值outer = get_outer_data(result)print(outer, type(outer))x1 = outer.iloc[:, 0]y1 = outer.iloc[:, 1]plt.scatter(x1, y1, marker='x', color='r') # 所有离散点plt.scatter(x, result, marker='.', color='g') # 异常点plt.plot([0, len(result)], [conf_intveral[0], conf_intveral[0]])plt.plot([0, len(result)], [conf_intveral[1], conf_intveral[1]])plt.show()4、采样点离散图和概率图import numpy as npimport matplotlib.pyplot as pltfrom scipy import statsimport pandas as pdimport timeprint(time.strftime('%Y-%m-%D %H:%M:%S'))# 根据均值、标准差,求指定范围的正态分布概率值def _normfun(x, mu, sigma):pdf = np.exp(-((x - mu)**2)/(2*sigma**2)) / (sigma * np.sqrt(2*np.pi))return pdf# 求列表数据的异常点def get_outer_data(data_list):df = pd.DataFrame(data_list, columns=['value'])df = df.iloc[:, 0]# 计算下四分位数和上四分位Q1 = df.quantile(q=0.25)Q3 = df.quantile(q=0.75)# 基于1.5倍的四分位差计算上下须对应的值low_whisker = Q1 - 1.5 * (Q3 - Q1)up_whisker = Q3 + 1.5 * (Q3 - Q1)# 寻找异常点kk = df[(df > up_whisker) | (df < low_whisker)]data1 = pd.DataFrame({'id': kk.index, '异常值': kk})return data1N = 100result = np.random.normal(0, 1, N)# result = np.random.randint(-65, 80, size=N) # 最⼩值,最⼤值,数量# result = [100]*100 # 取值全相同# result = np.array(result)mean, std = result.mean(), result.std(ddof=1) # 求均值和标准差# 计算置信区间,这⾥的0.9是置信⽔平if std == 0: # 如果所有值都相同即标准差为0则⽆法计算置信区间conf_intveral = [min(result)-1, max(result)+1]else:conf_intveral = stats.norm.interval(0.9, loc=mean, scale=std) # 90%概率# print('置信区间:', conf_intveral)# 求异常值outer = get_outer_data(result)# 绘制离散图fig = plt.figure()fig.add_subplot(2, 1, 1)plt.subplots_adjust(hspace=0.3)x = np.arange(0, len(result), 1)plt.scatter(x, result, marker='.', color='g') # 画所有离散点plt.scatter(outer.iloc[:, 0], outer.iloc[:, 1], marker='x', color='r') # 画异常离散点plt.plot([0, len(result)], [conf_intveral[0], conf_intveral[0]]) # 置信区间线条plt.plot([0, len(result)], [conf_intveral[1], conf_intveral[1]]) # 置信区间线条plt.text(0, conf_intveral[0], '{:.2f}'.format(conf_intveral[0])) # 置信区间数字显⽰plt.text(0, conf_intveral[1], '{:.2f}'.format(conf_intveral[1])) # 置信区间数字显⽰info = 'outer count:{}'.format(len(outer.iloc[:, 0]))plt.text(min(x), max(result)-((max(result)-min(result)) / 2), info) # 异常点数显⽰plt.xlabel('sample count')plt.ylabel('value')# 绘制概率图if std != 0: # 如果所有取值都相同fig.add_subplot(2, 1, 2)x = np.arange(min(result), max(result), 0.1)y = _normfun(x, result.mean(), result.std())plt.plot(x, y) # 这⾥画出理论的正态分布概率曲线plt.hist(result, bins=10, rwidth=0.8, density=True) # bins个柱状图,宽度是rwidth(0~1),=1没有缝隙info = 'mean:{:.2f}\nstd:{:.2f}\nmode num:{:.2f}'.format(mean, std, np.median(result))plt.text(min(x), max(y) / 2, info)plt.xlabel('value')plt.ylabel('Probability')else:fig.add_subplot(2, 1, 2)info = 'non-normal distribution!!\nmean:{:.2f}\nstd:{:.2f}\nmode num:{:.2f}'.format(mean, std, np.median(result))plt.text(0.5, 0.5, info)plt.xlabel('value')plt.ylabel('Probability')plt.savefig('./distribution.jpg')plt.show()print(time.strftime('%Y-%m-%D %H:%M:%S'))以上就是python ⽣成正态分布数据,并绘图和解析的详细内容,更多关于python 正态分布的资料请关注其它相关⽂章!。

正态分布函数的语法是NORMDIST(x,mean,standard_dev,cumulative)cumulative为一逻辑值,如果为0则是密度函数,如果为1则是累积分布函数。
如果画正态分布图,则为0。
例如均值10%,标准值为20%的正态分布,先在A1中敲入一个变量,假定-50,选中A列,点编辑-填充-序列,选择列,等差序列,步长值10,终止值70。
然后在B1中敲入NORMDIST (A1,10,20,0),返回值为0.000222,选中B1,当鼠标在右下角变成黑十字时,下拉至B13,选中A1B13区域,点击工具栏上的图表向导-散点图,选中第一排第二个图,点下一步,默认设置,下一步,标题自己写,网格线中的勾去掉,图例中的勾去掉,点下一步,完成。
图就初步完成了。
下面是微调把鼠标在图的坐标轴上点右键,选坐标轴格式,在刻度中填入你想要的最小值,最大值,主要刻度单位(x轴上的数值间隔),y轴交叉于(y 为0时,x多少)等等。
确定后,正态分布图就大功告成了。
PS:标准正态分布的语法为NORMSDIST(z),正态分布(一)NORMDIST函数的数学基础利用Excel计算正态分布,可以使用函数。
格式如下:变量,均值,标准差,累积,其中:变量:为分布要计算的值;均值:分布的均值;标准差:分布的标准差;累积:若1,则为分布函数;若0,则为概率密度函数。
当均值为0,标准差为1时,正态分布函数即为标准正态分布函数。
例3已知考试成绩服从正态分布,,,求考试成绩低于500分的概率。
解在Excel中单击任意单元格,输入公式:“ 500,600,100,1 ”,得到的结果为0.158655,即,表示成绩低于500分者占总人数的15.8655%。
例4假设参加某次考试的考生共有2000人,考试科目为5门,现已知考生总分的算术平均值为360,标准差为40分,试估计总分在400分以上的学生人数。
假设5门成绩总分近似服从正态分布。
制作直方图
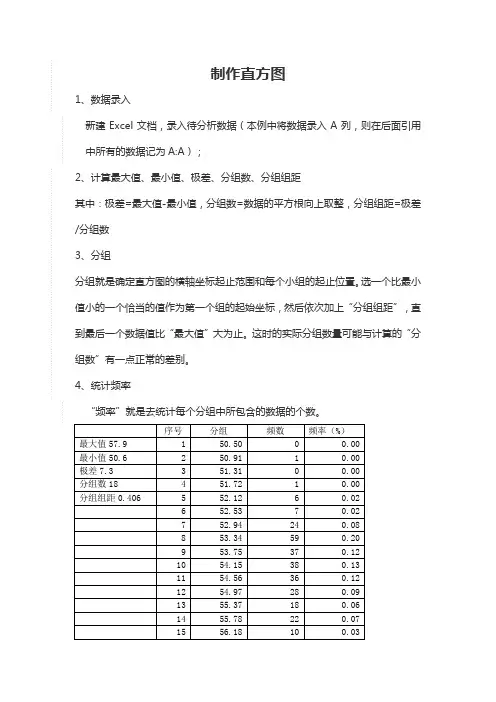
1、数据录入
新建Excel文档,录入待分析数据(本例中将数据录入A列,则在后面引用中所有的数据记为A:A);2
2、计算最大值、最小值、极差、分组数、分组组距
其中:极差=最大值-最小值,分组数=数据的平方根向上取整,分组组距=极差/分组数
3、分组
分组就是确定直方图的横轴坐标起止范围和每个小组的起止位置。
选一个比最小值小的一个恰当的值作为第一个组的起始坐标,然后依次加上“分组组距”,直到最后一个数据值比“最大值”大为止。
这时的实际分组数量可能与计算的“分组数”有一点正常的差别。
4、统计频率
5、制作直方图
选中统计好的直方图每个小组的分布个数的数据源(就是“频率”),用“柱形图”来完成直方图:选中频率列下所有数据(G1:G21),插入→柱形。



制作直方图
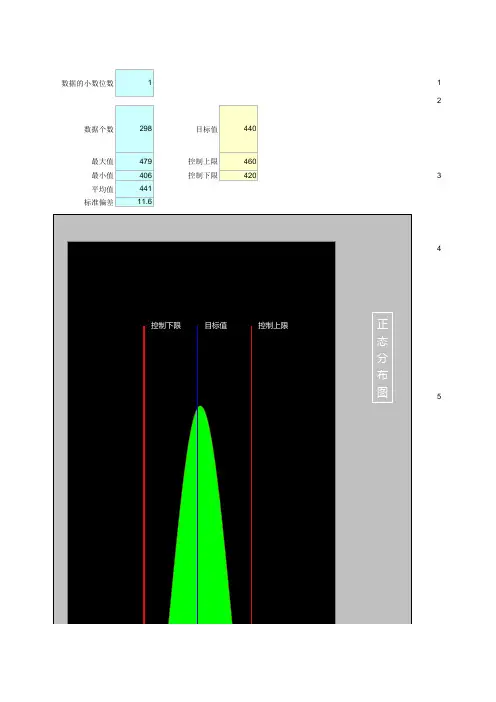
1、数据录入
新建Excel文档,录入待分析数据(本例中将数据录入A列,则在后面引用中所有的数据记为A:A);2
2、计算最大值、最小值、极差、分组数、分组组距
其中:极差=最大值-最小值,分组数=数据的平方根向上取整,分组组距=极差/分组数
3、分组
分组就是确定直方图的横轴坐标起止范围和每个小组的起止位置。
选一个比最小值小的一个恰当的值作为第一个组的起始坐标,然后依次加上“分组组距”,直到最后一个数据值比“最大值”大为止。
这时的实际分组数量可能与计算的“分组数”有一点正常的差别。
4、统计频率
5、制作直方图
选中统计好的直方图每个小组的分布个数的数据源(就是“频率”),用“柱形图”来完成直方图:选中频率列下所有数据(G1:G21),插入→柱形
选中正态分布柱形图→右键→更改系列图表类型,选中“拆线图”,确定。
选中正态分布曲线→右键→设置数据列格式→线型→勾选“平滑线”→关闭。
Excel表格中如何制作正态分布数据图和正态曲线模板Excel制作模板主要是方便直接使用,以后只要将新的样本数据替换,就可以随时做出正态分布图来,很简单。
以下是店铺为您带来的关于Excel表格中制作正态分布数据图和正态曲线模板,希望对您有所帮助。
Excel表格中制作正态分布数据图和正态曲线模板计算均值,标准差及相关数据1、假设有这样一组样本数据,存放于A列,首先我们计算出样本的中心值(均值)和标准差。
如下图,按图写公式计算。
为了方便对照着写公式,我在显示“计算结果”旁边一列列出了使用的公式。
公式直接引用A列计算,这样可以保证不管A列有多少数据,全部可以参与计算。
因为是做模板,所以这样就不会因为每次样本数据量变化而计算错误。
Excel在2007版本以后标准差函数有STDEV.S和STDEV.P。
STDEV.S是样本标准偏差,STDEV.P是基于样本的总体标准偏差。
如果你的Excel里没有STDEV.S函数,请使用STDEV函数。
2、正态分布直方图需要确定分组数,组距坐标上下限等。
如下图写公式计算。
分组数先使用25,上下限与中心值距离(多少个sigma)先使用4。
因为使用公式引用完成计算,所以这两个值是可以任意更改的。
这里暂时先这样放3、计算组坐标。
“组”中填充1-100的序列。
此处列了100个计算值。
原因后面再解释。
在G2,G3分别填入1,2。
选中G2,G3单元格,将鼠标放在右下角选中框的小黑方块上。
当鼠标变成黑色十字时,下拉。
直至数值增加至100。
如下两图4、如下图,H2输入公式=D9,H3单元格输入公式=H2+D$7。
为了使公式中一直引用D7单元格,此处公式中使用了行绝对引用。
5、选中H3单元格,将鼠标放在右下角选中框的小黑方块上。
当鼠标变成黑色十字时双击,填充H列余下单元格。
6、计算频数。
如图所示,在I2,I3分别填写公式计算频数。
同样,选中I3单元格,将鼠标放在右下角选中框的小黑方块上。
当鼠标变成黑色十字时双击,填充I列余下单元格。
利用Excel绘制正态分布曲线的实践正态分布是一种很重要的连续型随机变量的概率分布。
我们在生产中接触到的许多变量都是服从或近似服从正态分布的,如家畜的体长、体重、产奶量、产毛量、血红蛋白含量、血糖含量等。
许多统计分析方法都是以正态分布为基础的,因此在统计学中,正态分布无论在理论研究上还是实际应用中,均占有重要的地位。
但目前无论是网络还是其他参考资料,对正态分布曲线绘制的描述都不系统,对大多数人而言,绘制正态分布曲线依然是难点中的难点。
现以200头大白经产母猪所产仔猪一月龄窝重资料(见图1)为例,谈谈利用Excel绘制正态分布曲线的实践。
图1 200头大白经产母猪所产仔猪一月龄窝重资料1 直方图绘制直方图又称频率分布图,是一种显示数据分布情况的柱形图,可直观、快速地观察数据的分散程度和中心趋势。
直方图的频率计算和图形绘制有两种方式:一是计算数据频率并绘制直方图,二是使用数据分析工具生成直方图。
1.1 计算数据频率并绘制直方图第一步:利用Excel的COUNT、MAX、MIN、AVERAGE、STDEV函数,分别统计出数据个数、最大值、最小值、平均数、标准偏差。
第二部:统计出绘制直方图的基本参数。
在直方图基本参数中,最大值和最小值等于数据统计中的最大值和最小值,而“区间”,也就是“全距”,等于直方图的最大值与最小值的差;直方图的“柱数”,也就是“分组数”,一般等于数据个数的开方再加1(本例中是“SQRT(M2)+1”);组距一般是“区间”除以“直方图的柱数减1”(本例中是“H4/(H5-1)”)。
柱数和组距都取整数(见图2)。
第三步:计算制图数据。
其一是要计算分组数据。
在Excel 中,频数是按照“左开右闭”的方式对落在各区间的数据进行统计的,因此分组数据中要录入的是组上限值,要确保第一组分组数据中必须包含资料中的最小值,最后一个组必须包含资料中的最大值。
基于此,第一组的组上限值一般要大于、接近于资料中的最小值,且最好取整数。
excel2010正态分布的方法步骤图
在社会经济学问题中,有许多随机变量的概率分布都服从正态分布。
只要将一般正态分布转化为标准正态分布,查表,就能解决正态分布的概率。
下面让店铺为你带来excel2010设置正态分布的方法,希望对你有帮助!
excel2010正态分布设置的方法步骤
1、打开excel 2007,正态分布概率密度正态分布函数“NORMDIST”获取。
在这里是以分组边界值为“X”来计算:
Mean=AVERAGE(A:A)(数据算术平均)
Standard_dev=STDEV(A:A)(数据的标准方差)
Cumulative=0(概率密度函数)
2、向下填充。
3、在直方图内右键→选择数据→添加→系列名称:选中H1单元格;系列值:选中H2:H21;点击确定。
4、修整图形,在图表区柱形较下方选中正态分布曲线数据。
右键→设置数据列格式→系列绘制在→次坐标轴,完成。
Excel2010利用数据描点画图的步骤
将数据点坐标在工作簿中录入,一般为点(x,y)形式,体现在Excel中可以是两列数据。
附图为示例中的点。
在Excel2010中,选择插入带线的x,y散点图;
右键→选择数据,选好数据区域后,点击确定即可生成图表。
生成的图标为附图,由于我们习惯于坐标轴在左下方,所以此时将图标类型修改为折线图(带数据的堆积折线图)即可。
excel如何用制作对数正态分布的概率密度分布曲线图表推荐文章2021全运会场馆分布地点热度:犹太人为什么会被杀热度:高考地理的五种题型及特殊气候分布热度:高考二轮数学考点突破复习:概率与统计+解析几何热度:高考数学攻略:压轴题的考点分布及突破方法热度:验证事件的元素的对数正态分布性,一般可借助对数正态分布概率纸进行,若在概率纸上绘制的概率密度曲线为线性,那么该事件即呈对数正态分布。
以下是店铺为您带来的关于excel用制作对数正态分布的概率密度分布曲线图表,希望对您有所帮助。
excel用制作对数正态分布的概率密度分布曲线图表1、首先要做的是绘制正态分布刻度。
打开2013版excel,按自己的需要输入一系列累积分布值。
在”X轴网格值“那一列的第二个单元格中插入公式"NORM.S.INV"。
在弹出的窗口的"probability“处选一开始输入的系列累积分布值,选确定,空格,填充柄下拉,即得到正态刻度数值。
2、往三列第二个单元格输入0,填充柄填充。
以"X轴网格值”为横坐标,以第三列填充的0为纵坐标,做散点图。
作出的散点图如下图一,此时正态刻度以在X轴显示,接下来要调整坐标轴的格式。
3、选中横坐标轴,右击选“设置坐标轴格式”,在右边窗口的“最大值”“最小值”分别填“3.7194695”“-3.7194695”。
在“纵坐标轴交叉”处选“坐标轴值”,并输入数值“-3.7194695”,表示纵坐标和横坐标交叉于点(-3.7194695,0)。
调整后坐标如图4、接下来要做的就是要把累积分布值显示在横坐标上。
选中横坐标轴,删除。
选中横坐标轴线上的点,右击,选“添加数据标签”。
再一次选中轴上的点,右击,选“设置数据标签格式”。
在右边窗口“标签包括”先勾选“X值”,再把原有的“Y值”的勾去掉,并在“标签位置”选“靠下”。
完成上述步骤后,显示出来的数据为原始的X轴网格值,可通过手动修改,把想要显示的数据输入修改即可得到图三效果。