李雅普诺夫离散系统判据证明
- 格式:docx
- 大小:36.57 KB
- 文档页数:1



n维离散系统李雅普诺夫指数
在数学和动力系统理论中,n维离散系统的李雅普诺夫指数(Lyapunov exponent)是一种描述系统稳定性和混沌性质的重要指标。
它衡量了在系统的相空间中初始条件微小变化的指数增长率。
对于一个n维离散系统,设其状态变量为x=[x1, x2, ..., xn],时间步长为τ。
考虑一个由初始条件x0引起的微小扰动,用δx 表示,表示初始条件发生微小变化后得到的新状态变量。
通过迭代系统的动力学方程,可以得到δx的演化方程:
δx(t+τ) ≈ J(t) δx(t)
其中,J(t)表示系统在时间t处的雅可比矩阵,其定义为系统状态变量对于时间的导数。
李雅普诺夫指数λ定义为:λ = lim (1/t)log‖J(t)δx(0)‖
其中,t趋近于无穷大,‖‖表示向量的模。
李雅普诺夫指数的值可以为正、负或零,分别表示系统的指数增长、指数衰减或者不变。
n维离散系统的李雅普诺夫指数对于系统的稳定性和混沌性有着重要的意义。
当所有的李雅普诺夫指数都为负时,系统是稳定的;当至少一个李雅普诺夫指数为正时,系统是混沌的;而当所有的李雅普诺夫指数为零时,系统是边界稳定的或周期性的。
通过计算和分析系统的李雅普诺夫指数,可以揭示系统的
动力学性质,例如系统的稳定性、周期性还是混沌性质,并对系统的行为进行预测和控制。
因此,李雅普诺夫指数在动力系统理论和非线性科学领域有着广泛的应用。


离散时滞系统的渐近稳定性判据谭聚龙;张志维;杨德彬;高翔宇;张显【摘要】在已有文献的基础上,进一步研究离散时滞系统的渐近稳定性问题,通过选择合适的扩展李亚雅诺夫泛函,获得了基于线性矩阵不等式的时滞相关的稳定性判据.对现有的方法进行了改进,即将时滞区间进行了划分,在小的区间上对李雅普诺夫泛函进行处理.通过比较可知,所给出的稳定性判据比存在的稳定性判据具有更弱的保守性.通过数值实例验证了所得结论的有效性.【期刊名称】《黑龙江大学自然科学学报》【年(卷),期】2015(032)006【总页数】7页(P753-759)【关键词】离散时滞系统;渐近稳定性;李雅普诺夫泛函【作者】谭聚龙;张志维;杨德彬;高翔宇;张显【作者单位】黑龙江大学数学科学学院,哈尔滨150080;哈尔滨华德学院电子与信息工程学院,哈尔滨150025;哈尔滨华德学院通识教育学院,哈尔滨150025;黑龙江大学数学科学学院,哈尔滨150080;黑龙江大学数学科学学院,哈尔滨150080【正文语种】中文【中图分类】TP13时滞现象经常出现在通信系统、生物系统、过程控制系统中[1-2],几乎所有的实际问题都是在系统稳定的前提下来研究其性能的。
稳定性是时滞系统的一个重要性质,稳定性分析成为研究时滞系统的首要任务,已经取得了一些成果[3-11]。
许多文献给出了不同方法来分析时滞系统的稳定性,主要目的是扩大使得时滞系统稳定的时滞变化区间,从而降低稳定性判据的保守性。
许多学者已经提出了获得时滞相关的稳定性判据的各种方法,主要包括Jensen不等式方法、自由权矩阵方法、时滞分解方法、扩展Lyapunov-Krasovskii泛函方法、凸组合方法、离散Lyapunov泛函方法、倒凸组合方法等,其中Jensen不等式方法、自由权矩阵方法、时滞分解方法已经被广泛使用。
文献[4-6]结合自由权矩阵方法和积分不等式方法,给出了时滞系统的稳定性判据,并且较以往的文献具有更弱的保守性。



讲义81. 李雅普诺夫(Lyapunov )函数分析本讲中,对于一些有*E (,)0t S r w ⎡⎤=⎣⎦的*γ,我们研究1(,)t t t t t r r S r w γ+=+的收敛性。
回顾一下确定性实例中的Lyapunov 函数分析,我们选取了函数()V r 使得** ()0, ,()()0, , ()0.T V r r V r S r r r V r •≥∀•∇<≠•∇=如收敛性的论证为:我们发现()t V r 随时间减小并且有下限,因此,()t V r 收敛。
对V 和S 采用技术条件,可以证明*t r r →。
现在转到随机实例,用t F 表示到t 时刻的过程历史记录,显然,t F 可表示为{},,,,,,.t l l t r l t w l t l t γ=≤<≤F注意,步长t γ依赖于随机的历史记录,而步依赖于扰动t w 。
定义欧几里德范数122()T V V V =。
定理1 假设V ∃使得(a )()0, ,V r r ≥∀(b )L ∃使得22()()V r V r L r r ∇−∇≤−(李普希茨连续Lipschitz continuity) (c )12,K K ∃使得221222E (,)(),t t t t S r w K K V r ⎡⎤≤+∇⎣⎦F(d )c ∃使得22()E (,)().T t t t t t V r S r w c V r ∇⎡⎤≤−∇⎣⎦F 则,如t γ满足0t t γ∞==∞∑和20t t γ∞=<∞∑,有z ()t V r 收敛。
z lim ()0t t V r →∞∇=z 每一个t r 的极限点r 满足()0V r ∇=我们将证明某特例的收敛性,该特例对于一些*r 有2*122()V r r r =−。
定理2 假设2*122()V r r r=−满足(a )12,K K ∃使得2122E (,)(),t t t t S r w K K V r ⎡⎤≤+⎣⎦F(b )c ∃使得()E (,)().T t t t t t V r S r w cV r ∇⎡⎤≤−⎣⎦F则,如t γ满足0t t γ∞==∞∑和20t t γ∞=<∞∑,有*t r r →, w.p.1(以概率1)我们用下面的上鞅收敛定理证明定理2。

离散条件下的李雅普诺夫稳定判据1. 概述在控制论与系统论中,稳定性是一个重要的概念。
在研究动态系统的稳定性时,我们常常需要使用稳定性判据来判断系统的稳定性。
而在离散条件下,李雅普诺夫稳定判据就是一个常用的方法。
2. 李雅普诺夫稳定判据的定义李雅普诺夫稳定判据是由俄罗斯数学家亚科夫•伊万诺维奇•李雅普诺夫在稳定性理论中提出的一种判据。
它用于判断差分方程系统在离散条件下的稳定性。
3. 离散条件下的稳定性在离散条件下,系统的状态是以离散的时间点进行更新的。
这种情况下,我们常常需要研究系统的稳定性,即系统在经过一定次数的状态更新后,是否能趋向于某一稳定状态,或者在一定范围内波动。
而李雅普诺夫稳定判据就是用来判断这种系统的稳定性的一种方法。
4. 李雅普诺夫稳定判据的原理李雅普诺夫稳定判据的核心思想是通过构造一个Lyapunov函数来判断系统的稳定性。
对于一个给定的系统,如果存在一个 Lyapunov 函数,满足对系统的任意状态进行更新后,Lyapunov 函数的值都会减小,那么系统就是稳定的。
5. Lyapunov 函数的选择在使用李雅普诺夫稳定判据时,选择合适的Lyapunov 函数是至关重要的。
一般来说,Lyapunov 函数的选择是根据系统的特点来确定的。
常见的 Lyapunov 函数包括二次型函数、指数型函数等。
不同的Lyapunov 函数对系统的稳定性判断有不同的适用条件和效果。
6. 李雅普诺夫稳定判据的应用李雅普诺夫稳定判据在控制论与系统论中有着广泛的应用。
通过使用李雅普诺夫稳定判据,我们可以对离散条件下的系统进行稳定性分析,为系统的设计与控制提供理论支持。
7. 结论离散条件下的李雅普诺夫稳定判据是系统稳定性分析中的重要工具,通过对系统的 Lyapunov 函数进行构造和分析,我们可以判断系统是否稳定,并为系统的设计与控制提供理论依据。
希望本文的介绍对您有所帮助。
基于离散条件下的李雅普诺夫稳定判据,我们将进一步探讨该方法的具体应用和细节,以及其对控制系统和动态系统的实际意义。

.现代控制理论实验报告组员:院系:信息工程学院专业:指导老师:年月日实验1 系统的传递函数阵和状态空间表达式的转换[实验要求]应用MATLAB 对系统仿照[例1.2]编程,求系统的A 、B 、C 、阵;然后再仿照[例1.3]进行验证。
并写出实验报告。
[实验目的]1、学习多变量系统状态空间表达式的建立方法、了解系统状态空间表达式与传递函数相互转换的方法;2、通过编程、上机调试,掌握多变量系统状态空间表达式与传递函数相互转换方法。
[实验内容]1 设系统的模型如式(1.1)示。
p m n R y R u R x DCx y Bu Ax x ∈∈∈⎩⎨⎧+=+= (1.1)其中A 为n ×n 维系数矩阵、B 为n ×m 维输入矩阵 C 为p ×n 维输出矩阵,D 为传递阵,一般情况下为0,只有n 和m 维数相同时,D=1。
系统的传递函数阵和状态空间表达式之间的关系如式(1.2)示。
D B A SI C s den s num s G +-==-1)()()(()( (1.2)式(1.2)中,)(s num 表示传递函数阵的分子阵,其维数是p ×m ;)(s den 表示传递函数阵的按s 降幂排列的分母。
2 实验步骤① 根据所给系统的传递函数或(A 、B 、C 阵),依据系统的传递函数阵和状态空间表达式之间的关系如式(1.2),采用MATLA 的file.m 编程。
注意:ss2tf 和tf2ss 是互为逆转换的指令;② 在MATLA 界面下调试程序,并检查是否运行正确。
③ [1.1] 已知SISO 系统的状态空间表达式为(1.3),求系统的传递函数。
,2010050010000100001043214321u x x x x x x x x ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡ []⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=43210001x x x x y (1.3)程序:A=[0 1 0 0;0 0 -1 0;0 0 0 1;0 0 5 0]; B=[0;1;0;-2]; C=[1 0 0 0]; D=0;[num,den]=ss2tf(A,B,C,D,1)程序运行结果:num =0 -0.0000 1.0000 -0.0000 -3.0000 den =1.0000 0 -5.0000 0 0从程序运行结果得到:系统的传递函数为:24253)(ss s S G --= ④ [1.2] 从系统的传递函数式求状态空间表达式。
李雅普诺夫离散系统判据证明
李雅普诺夫判据是用来证明离散系统稳定性的一种方法。
该判据是基于李雅普诺夫函数的变化性质进行证明的。
首先,假设离散系统的状态变量为x,其演化方程为x(k+1) =
f(x(k)),其中k为离散时间步。
如果存在一个函数V(x),满足
以下条件:
1. V(x)是定义在状态空间D内的连续函数;
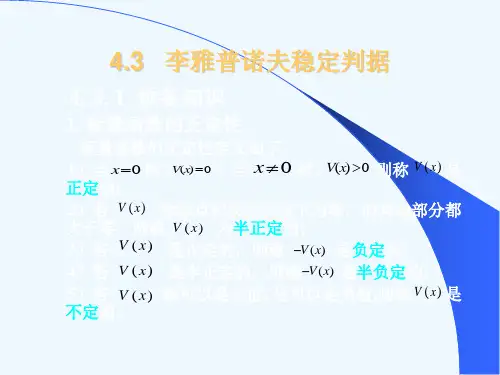
2. V(x)在D中严格正定,即V(x) > 0,对于任何非零的x;
3. 对于所有的x(k)满足x(k+1) = f(x(k)),有V(x(k+1)) ≤ V(x(k)) - α(x(k)),其中α(x(k))是一个正定的函数;
4. 如果存在一个正定的函数β(x)满足V(x(k)) ≤ β(x(k)),则系
统是渐近稳定的。
根据以上条件,可以证明系统的稳定性。
具体证明的步骤如下:
1. 首先,确定适合的Lyapunov函数V(x)。
这可以通过系统的
特性和性质进行推导和选择,例如能量函数、误差函数等;
2. 推导出V(x(k+1))和V(x(k))之间的关系式,并解析得到
α(x(k))的表达式;
3. 根据V(x(k+1)) ≤ V(x(k)) - α(x(k)),证明V(x)是单调递减的;
4. 通过比较V(x)和β(x)的形式,得出V(x(k)) ≤ β(x(k))的结论;
5. 根据Lyapunov函数的性质,证明系统是渐近稳定的。
需要注意的是,李雅普诺夫判据只能证明系统的稳定性,不能推导出系统的收敛速度。