下载文档原格式
第四章稳定性与李雅普诺夫方法稳定性与李雅普诺夫方法是控制理论中的两个重要概念。
稳定性是控制系统分析中的基本问题之一，它描述了系统在受到干扰后能否回到平衡状态的能力。
李雅普诺夫方法是一种常用的稳定性分析方法，通过构造李雅普诺夫函数来判断系统的稳定性。
稳定性是控制系统设计中最基本的要求之一、一个稳定的系统能够在受到干扰后迅速恢复到平衡状态，而不会发生不可控制的震荡或不稳定的行为。
稳定性可以分为两种类型：渐近稳定性和有界稳定性。
渐近稳定性要求系统的状态能够收敛到一个稳定的平衡点，而有界稳定性要求系统的状态能够保持在一个有限范围内。
李雅普诺夫方法是一种通过构造李雅普诺夫函数来判断系统稳定性的方法。
李雅普诺夫函数是一个标量函数，它满足以下条件：1)对于任意非零的向量，李雅普诺夫函数的导数都是负的或零；2)当且仅当系统达到稳定时，李雅普诺夫函数的导数为零。
通过构造李雅普诺夫函数并分析其导数的符号，可以判断系统的稳定性。
在实际应用中，人们通常使用李雅普诺夫直接法、李雅普诺夫间接法和李雅普诺夫-克拉洛夫稳定性定理等方法来进行稳定性分析。
其中，李雅普诺夫直接法是最常用的方法之一，它通过选择一个合适的李雅普诺夫函数来判断系统的稳定性。
如果可以找到一个李雅普诺夫函数，使得该函数的导数对于所有非零的初始条件都是负的，则系统是渐近稳定的。
李雅普诺夫间接法是通过构造一个李雅普诺夫方程来判断系统的稳定性。
李雅普诺夫方程是一个微分方程，其中包含系统的状态向量和一个非负标量函数，满足一定的条件。
如果可以找到一个满足李雅普诺夫方程的解，并且该解是有界的，则系统是有界稳定的。
李雅普诺夫-克拉洛夫稳定性定理是李雅普诺夫方法的重要理论基础。
该定理表明，如果系统的李雅普诺夫函数存在并且连续可导，并且李雅普诺夫函数的导数满足一定的条件，则系统是渐近稳定的。
这个定理为李雅普诺夫方法的应用提供了重要的理论依据。
总之，稳定性与李雅普诺夫方法是控制理论中基础且重要的概念。
李雅普诺夫稳定性方法
李雅普诺夫第一方法又称间接法，它是通过系统状态方程的解来判断系统的稳定性。
如果其解随时间而收敛，则系统稳定；如果其解随时间而发散，则系统不稳定。
李雅普诺夫第二方法又称直接法，它不通过系统状态方程的解来判断系统的稳定性，而是借助李雅普诺夫函数对稳定性作出判断，是从广义能量的观点进行稳定性分析的。
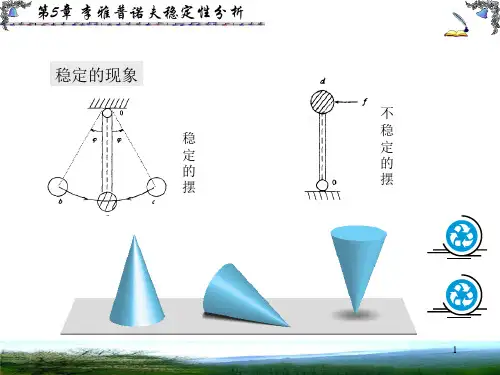
例如有阻尼的振动系统能量连续减小（总能量对时间的导数是负定的），系统会逐渐停止在平衡状态，系统是稳定的。
由于李雅普诺夫第一方法求解通常很烦琐，因此李雅普诺夫第二方法获得更广泛的应用。
李雅普诺夫第二方法的难点在于寻找李雅普诺夫函数。
迄今为止，尚没有通用于一切系统的构造李雅普诺夫函数的方法。
对于系统[]t ,f x x
= ，平衡状态为,0e =x 满足()0f e =x 。
如果存在一个标量函数()x V ,它满足()x V 对所有x 都具有连续的
一阶偏导数；同时满足()x V 是正定的；则 （1）若()x V 沿状态轨迹方向计算的时间导数()dt /)(dV V
x x = 为半负定，则平衡状态稳定；
（2） 若()x V 为负定，或虽然()x V 为半负定，但对任意初始状
态不恒为零，则平衡状态渐近稳定。
进而当∞→∞→)(V x x 时，，则系统大范围渐近稳定；
（3） 若()x V
为正定，则平衡状态不稳定。
判断二次型
x x x P )(V τ=的正定性可由赛尔维斯特
（Sylvester ）准则来确定，即正定（记作V(x)>0）的充要条件为P 的所有主子行列式为正。
如果P 的所有主子行列式为非负，为正半定（记作V(x)≥0）；如果-V(x)为正定,则V(x)为负定（记作V(x)<0）；如果-V(x)为正半定,则V(x)为负半定（记作V(x)≤0）。
例：
[]正定。
则)(V 01121412
110,04
1110,010x x x 1121412110x x x )(V 321321x x >---->>----=⎥⎥⎦
⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡ 例：
)x x (x x x )
x x (x x x 22212122221121+--=+-=
(0,0）是唯一的平衡状态。
设正定的标量函数为
∞→∞→<+-=+--++-=+=∂∂+∂∂=+=)V(,且当0
)x 2(x )]x (x x x [2x )]x (x x [x 2x x 2x x
2x dt
dx x V dt dx x V )(V x x )V(2222122212122221121221122112
2
21x x x x
故系统在坐标原点处为大范围渐近稳定。
