李雅普诺夫稳定性的基本定理
- 格式:ppt
- 大小:240.00 KB
- 文档页数:3



李雅普诺夫稳定性特征根分布
李雅普诺夫稳定性特征根分布在系统控制领域被广泛研究,并被广泛应用在科
学和工程中。
李雅普诺夫稳定性特征根分布是对一个系统的稳定性的影响因素的研究和分析。
李雅普诺夫稳定性特征根分布可以通过一个表达式来表示:λn=(-
βn)+(α+(2π/πn))^2,其中λn为特征根,εn为特征值,α为系统系数,和
πn为系统周期。
它表示了系统的稳定性特征根分布和稳定性特征值分布之间的关系。
由于特征根和特征值严格地反映了一个系统的稳定性,所以李雅普诺夫稳定性
特征根分布被用于分析一个系统的稳定性。
该分布一般包括一个特征根的实部和虚部,它们的关系可以描述为:如果特征根的实部都大于零,则系统是稳定的;如果特征根的实部小于零,则系统是不稳定的;如果特征根的实部有正有负,则系统就会出现振荡。
为了检验一个系统的稳定性,通常先用信号在控制系统上模拟,然后计算系统
的特征根和特征值,并绘制出李雅普诺夫稳定特征根分布图表。
通过该图表分析,如果特征根的实部均大于零,则系统的稳定性得到证明;如果有负特征根,则系统就是不稳定的。
通过李雅普诺夫稳定性特征根分布曲线,在一定程度上可以反映出系统稳定性,从而用于系统状态的判断,以此为基础,改正或调节系统,提高系统的效率,获得更好的性能。
因此,李雅普诺夫稳定性特征根分布在系统应用和控制中有着重要的应用,为后续的系统控制工作提供了可取的依据。

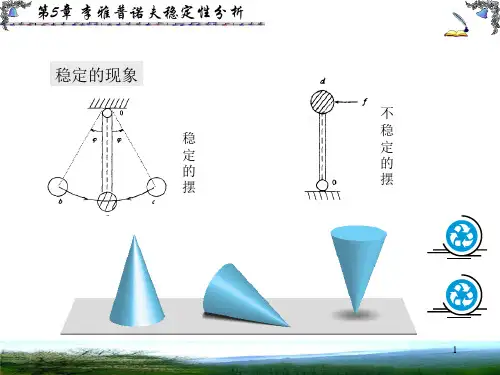
第六章 李雅普诺夫稳定性分析在反馈控制系统的分析设计中,系统的稳定性是首先需要考虑的问题之一。
因为它关系到系统是否能正常工作。
经典控制理论中已经建立了劳斯判据、Huiwitz 稳定判据、Nquist 判据、对数判据、根轨迹判据等来判断线性定常系统的稳定性,但不适用于非线性和时变系统。
分析非线性系统稳定性及自振的描述函数法,则要求系统的线性部分具有良好的滤除谐波的性能;而相平面法则只适合于一阶、二阶非线性系统。
1892年俄国学者李雅普诺夫(Lyapunov )提出的稳定性理论是确定系统稳定性的更一般的理论,它采用状态向量来描述,不仅适用于单变量、线性、定常系统,还适用于多变量、非线性、时变系统。
§6-1 外部稳定性和内部稳定性系统的数学模型有输入输出描述(即外部描述)和状态空间描述(即内部描述),相应的稳定性便分为外部稳定性和内部稳定性。
一、外部稳定性1、定义(外部稳定性):若系统对所有有界输入引起的零状态响应的输出是有界的,则称该系统是外部稳定的。
(外部稳定性也称为BIBO (Bounded Input Bounded Output )稳定性) 说明:(1)所谓有界是指如果一个函数)(t h ,在时间区间],0[∞中,它的幅值不会增至无穷,即存在一个实常数k ,使得对于所有的[]∞∈0t ,恒有∞<≤k t h )(成立。
(2)所谓零状态响应,是指零初始状态时非零输入引起的响应。
2、系统外部稳定性判据线性定常连续系统∑),,(C B A 的传递函数矩阵为Cxy Bu Ax x=+=BUA sI X BU X A sI CX Y BU AX sX 1)()(--==-=+=B A sIC s G 1)()(--=当且仅当)(s G 极点都在s 的左半平面内时,系统才是外部稳定(或BIBO 稳定)的。
【例6.1.1】已知受控系统状态空间表达式为u x x ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-=121160 , []x y 10= 试分析系统的外部稳定性。

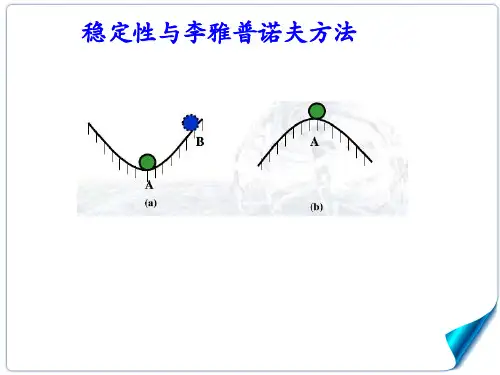
李雅普诺夫第二法李雅普诺夫第二法又称直接法,它是从能量观点进行稳定性分析的,它的基本思想是建立在这样一个物理事实基础之上,即:由经典力学理论可知,对于一个振动系统,如果系统的总能量随时间增长而连续减少,直到平衡状态为止,那么振动系统是稳定的。
1)渐进稳定的判据定理1设系统的状态方程为(,)x f x t =其中平衡状态为0e x =,满足(0,)0f t =,如果存在一个具有连续一阶偏导数的标量函数(,)v x t ,且满足以下条件:(1)(,)v x t 是正定的;(2)(,)vx t 是负定的。
则系统在原点处的平衡状态是一致渐进稳定的。
此外,如果当||||x →∞,有(,)v x t →∞,则在原点处的平衡状态是大范围一致渐进稳定的。
2)渐进稳定的判据定理1设系统的状态方程为(,)x f x t =其中平衡状态为(0,)0f t =,如果存在一个具有连续一阶偏导数的标量函数(,)v x t ,且满足以下条件:(1)(,)v x t 是正定的;(2)(,)vx t 是负定的。
(3)(,)v x t 在0x ≠时不恒等于零,则系统在原点处的平衡状态是大范围渐进稳定的。
3)李雅普诺夫意义下稳定的判别定理设系统的状态方程为=x f x t(,)其中平衡状态为(0,)0f t=,如果存在一个具有连续一阶偏导数的标量函数v x t,且满足以下条件:(,)(1)(,)v x t是正定的;(2)(,)是负定的。
v x t(3)则系统在原点处的平衡状态在李雅普诺夫意义下是一致稳定的。
4)不稳定的判别定理设系统的状态方程为=x f x t(,)其中平衡状态为(0,)0f t=,如果存在一个具有连续一阶偏导数的标量函数v x t,且满足以下条件:(,)(1)(,)v x t是正定的;(2)(,)是正定的。
v x t则系统在原点处的平衡状态是不稳定。



