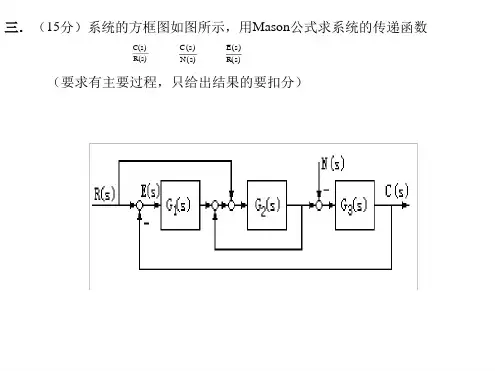
利用梅森公式求传递函数

梅森公式求传递函数
梅森公式是一种常用的求解数字滤波器传递函数的方法。

数字滤波器是一种用于数字信号处理的滤波器，其传递函数描述了滤波器对输入信号的影响。

梅森公式可以用于求解各种类型的数字滤波器的传递函数，包括低通、高通、带通和带阻滤波器。

梅森公式的基本形式为：
H(z) = B(z) / A(z)
其中，B(z)和A(z)分别为数字滤波器的分子和分母多项式。

通过对分子和分母多项式进行系数的选择和取值，可以得到不同类型的数字滤波器传递函数。

例如，对于一个二阶低通数字滤波器，其分母多项式可以表示为： A(z) = 1 + a1*z^-1 + a2*z^-2
其中，a1和a2为系数。

通过选择合适的系数值，可以得到所需的滤波器响应特性。

类似地，分子多项式可以表示为：
B(z) = b0 + b1*z^-1 + b2*z^-2
也需要根据需要的响应特性进行系数的选择。

将分子和分母多项式代入梅森公式，即可求得数字滤波器的传递函数。

需要注意的是，在使用梅森公式求解数字滤波器传递函数时，需要考虑数字滤波器的采样率、截止频率等参数，以确保所得到的传递函数具有所需的滤波性能。

同时，由于数字滤波器的传递函数是离散的，因此在实际应用中需要进行数字信号的抽样和插值等处理，以确保信号处理的准确性和精度。

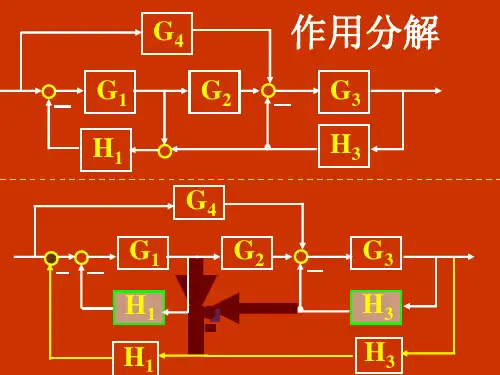
是包含于，你理解的有点偏差，举个例子如果有三个互不接触的回路，取两个不接触的回路应有三项，取三个互不接触回路就一项。

具体的应该是这样：
梅森公式G(s)=Σ(Ρκ*△κ)╱△G(s)= ——系统总传递函数；n——是前向通道数；Ρκ——第k条前向通路的传递函数，由输入端单向传递至输出端的信号通道称为前向通道；△——流图的特征式△=1-ΣLi+ΣLjLk-ΣLiLjLk+······
L A
bc为每两个不接触回路增益乘积之和
a为所有回路增益之和；L a L b
Li——所有单独回路的增益之和；
LjLk——所有互不接触的单独回路中，取其中两个不接触的回路增益乘积之和；LiLjLk——所有互不接触的单独回路中，取三个互不接触回路增益之和；
△κ——第k条前向通路特征式的余因子，即对于流图的特征式△，将与第k 条前向通路相接触的回路
增益代以零值，余下的即为△κ。

对于复杂的结构，理论上有很多项，但实际上△就取到前两三项。

3.梅森公式
对于一个确定的信号流图或方框图，应用梅森公式可以直接求得输入变量到输出变量的系统传递函数。

梅森公式可表示为
（3.78）
式中——系统总传递函数；
——第条前向通路的传递函数；
——流图的特征式
式中——所有不同回路的传递函数之和；
——每两个互不接触回路传递函数乘积之和；
——每三个互不接触回路传递函数乘积之和；
——第条前向通路特征式的余因子，即对于流图的
特征式，将与第条前向通路相接触的回路
传递函数代以零值，余下的即为。

下面通过求图3.48f所示二级电路网络信号流图的传递函数来说明梅森公式的用法。

这个系统中，输入变量与输出变量之间只有一条前向通道，其传递函数为
信号流图里有三个不同回路，它们的传递函数分别为
回路不接触回路（回路接触回路，并且回路接触回路），因此，流图特征式为
（3.79）
从中将与通道接触的回路传递函数、和都代以零值，即可获得余因子。

因此，得到
所以
（3.80）
将式（3.79）和式（3.80）代入式（3.78）便可得到二级电路网络的系统传递函数，即。

梅森公式求传递函数梅森公式求传递函数在探讨开环传递函数和闭环传递函数之前，我们需要先了解一些基础知识。

传递函数通常是指线性系统的输出与输入之间的关系，其中输入通常是一个函数，输出也是一个函数。

当我们了解传递函数的性质时，我们可以更好地设计控制系统，调整输入，使输出达到我们所需的目标。

在这里，我们将重点介绍梅森公式是如何求解传递函数的，梅森公式是一种常见的、快速且可靠的方法，用于解决反馈控制系统的稳定性问题。

梅森公式是一种特殊的公式，它同时适用于电气和机械系统，尤其适用于系统的加减法运算芯片，用于测量和放大信号。

首先，我们需要了解梅森公式的组成部分——单位环，单位环是指输入信号沿着反馈路径回到输入的路径。

这通常是因为系统的输出通过反馈路径的增强或减弱，来调节系统的调制。

如果我们能够计算出反馈路径的增强和输入信号的比例，我们就可以确定系统的传递函数了。

那么，如何确定反馈路径的增强和输入信号的比例呢？这就需要用到梅森公式了。

梅森公式表明，任何一个带有反馈路径的系统都可以由输入的单位环来描述。

在这种情况下，反馈系数是最小的。

因此，我们可以通过计算单位环的增益和相位移，来确定系统的传递函数。

梅森公式的常见形式为：$H(s) = \frac{N(s)}{D(s)} =\frac{1}{\Delta}\sum_{i=1}^{n}(-1)^{i+1}\Delta_i(s)\frac{D_i(s)}{N_i(s)}$其中，$\Delta$为通分多项式，$D(s)$为系统的分母多项式，$N(s)$为系统的分子多项式，$D_i(s)$和$N_i(s)$为单位环考虑时的分母多项式和分子多项式，$\Delta_i(s)$为通分多项式的第$i$个因式。

这个梅森公式看起来很复杂，但它告诉我们的是，我们可以把系统的分子多项式和分母多项式分解成多个分式（即$\frac{D_i(s)}{N_i(s)}$），然后通过单位环考虑时，根据各个分式的反馈系数（即$(-1)^{i+1}$）和分式的分母和分子多项式得到系统的传递函数。