专题5 梅森增益公式

梅森增益公式适用范围标题：梅森增益公式适用范围的阐述引言：梅森增益公式是电子电路设计中常用的一种分析工具，用于计算电路增益和频率响应。

然而，在实际应用中，梅森增益公式的适用范围有一定限制。

本文将就梅森增益公式的适用范围展开阐述，以帮助读者更好地理解和使用这一公式。

一、梅森增益公式简介梅森增益公式是一种基于网络理论的公式，用于计算复杂电路的总增益。

它是由美国电子工程师梅森提出的，一般用于线性、定常、时不变的电路分析。

二、适用范围的限制1. 线性电路要求梅森增益公式适用于线性电路，即电路的元件和信号是线性的。

对于非线性电路，例如包含二极管、晶体管等非线性元件的电路，梅森增益公式就不再适用。

2. 定常电路要求第1页/共6页梅森增益公式适用于定常电路，即电路的参数是固定的，不随时间变化。

对于具有非定常特性的电路，如含有开关、变阻器等可变元件的电路，梅森增益公式无法提供准确的结果。

3. 时不变电路要求梅森增益公式适用于时不变电路，即电路的参数与时间无关。

在实践中，例如考虑温度变化、电源变化等因素会导致电路参数发生改变，因此这些情况下梅森增益公式不能得到准确的结果。

三、梅森增益公式的优势尽管梅森增益公式存在一定的适用范围限制，但它仍然是电子电路设计中常用的工具。

以下是梅森增益公式的一些优势：1. 简单易用相比其他复杂的电路分析方法，梅森增益公式简单易懂，计算过程相对简单直观。

这使得它成为工程师们在电路设计、故障排除等方面的重要工具。

2. 可模块化分析梅森增益公式支持对电路进行模块化分析。

通过将复杂的电路划分为多个子电路，可以使用梅森增益公式计算每个子电路的增益，进而得到整个电路的总增益。

这种分析方法便于对电路进行优化和调试。

第2页/共6页3. 提供定量分析结果梅森增益公式给出的是数值化的增益结果，可以帮助工程师量化地评估和比较不同电路的性能。

这对于电路设计者来说非常重要，可以在设计初期对各个子电路进行评估和优化。

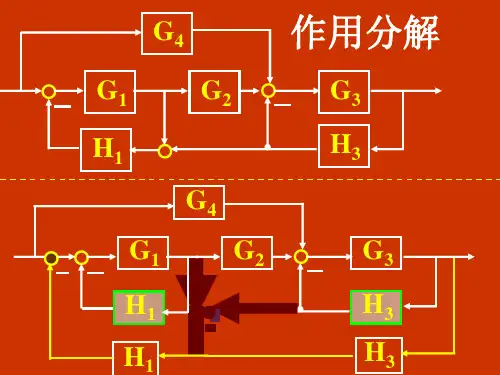
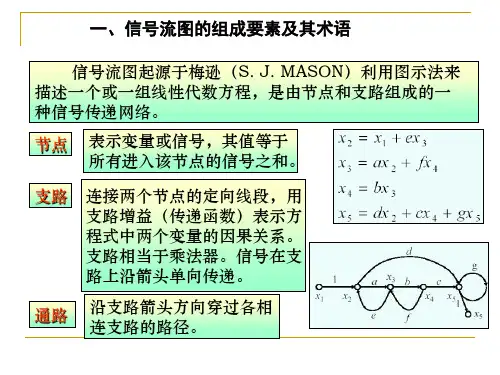
6-5 系统的信号流图与梅森公式一、信号流图的定义由节点与有向支路构成的能表征系统功能与信号流动方向的图，称为系统的信号流图，简称信号流图或流图。

例如，图6-29(a)所示的系统框图，可用图6-29(b)来表示，图(b)即为图(a)的信号流图。

图(b)中的小圆圈“o”代表变量，有向支路代表一个子系统及信号传输(或流动)方向，支路上标注的H(s)代表支路(子系统)的传输函数。

这样，根据图6-29(b)，同样可写出系统各变量之间的关系，即图6-29二、三种运算器的信号流图表示三种运算器：加法器、数乘器、积分器的信号流图表示如表6-3中所列。

由该表中看出：在信号流图中，节点“o”除代表变量外，它还对流入节点的信号具有相加(求和)的作用，如表中第一行中的节点Y(s)即是。

三、模拟图与信号流图的相互转换规则模拟图与信号流图都可用来表示系统，它们两者之间可以相互转换，其规则是：(1) 在转换中，信号流动的方向(即支路方向)及正、负号不能改变。

(2) 模拟图(或框图)中先是“和点”后是“分点”的地方，在信号流图中应画成一个“混合”节点，如图6-30所示。

根据此两图写出的各变量之间的关系式是相同的，即。

(3) 模拟图(或框图)中先是“分点”后是“和点”的地方，在信号流图中应在“分点”与“和点”之间，增加一条传输函数为1的支路，如图6-31所示。

(4) 模拟图(或框图)中的两个“和点”之间，在信号流图中有时要增加一条传输函数为1的支路(若不增加，就会出现环路的接触，此时就必须增加)，但有时则不需增加(若不增加，也不会出现环路的接触，此时即可以不增加。

见例6-17)。

(5) 在模拟图(或框图)中，若激励节点上有反馈信号与输入信号叠加时，在信号流图中，应在激励节点与此“和点”之间增加一条传输函数为1的支路(见例6-17)。

(6) 在模拟图(或框图)中，若响应节点上有反馈信号流出时，在信号流图中，可从响应节点上增加引出一条传输函数为1的支路(也可以不增加，见例6-17)。

具有任意条前向通路及任意个单独回路和不接触回路的复杂信号流图，求取从任意源节点到任意阱节点之间传递函数的梅森增益公式记为
式中
——从源节点到阱节点的传递函数（或总增益）；
——从源节点到阱节点的前向通路总数；
——从源节点到阱节点的第
条前向通路总增益；
——流图特征式
式中
——所有单路回路增益之和；
——所有互不接触的单独回路中，每次取其中两个回路的回路增益的乘积之和；
——所有互不接触的单独回路中，每次取其中三个回路的回路增益的乘积之和；
——流图余因子式，它等于流图特征式中除去与第
条前向通路相接触的回路增益项（包括回路增益的乘积项）以后的余项式。

[1]。

简易梅森公式好的，以下是为您生成的关于“简易梅森公式”的文章：梅森公式，这玩意儿听起来好像有点高大上，让人摸不着头脑，但其实呀，它就像一个藏在数学城堡里的小秘密，等我们去揭开它的神秘面纱。

我记得有一次给学生们讲梅森公式的时候，那场面可有意思啦。

当时我在黑板上写下了一堆复杂的公式和符号，学生们的眼神从期待瞬间变成了迷茫，一个个小脑袋瓜里估计都在想：“这是啥呀？”我赶紧打住，说：“同学们，别慌，咱们慢慢来。

”然后我就从最基础的概念开始讲起。

咱们先来说说啥是梅森公式。

它呀，其实就是用来计算线性系统传递函数中分母多项式的特征根的个数。

听起来是不是还是有点晕？没关系，咱们举个例子。

比如说有一个系统，它的传递函数分母多项式是 s^3 + 2s^2 + 3s + 4 ，咱们用梅森公式就能很快算出这个多项式有几个根。

那梅森公式到底长啥样呢？它大概是这样的：Pk 表示第 k 条前向通路的传递函数，Δ 表示特征式，Δk 表示第 k 条前向通路特征式的余子式。

哎呀，光说这些公式和概念，估计你们都快睡着了。

咱们还是回到刚刚那个例子。

我当时就一步一步地带着学生们，把每一项都算出来，然后得出最终的结果。

在这个过程中，有个平时挺调皮的学生，突然瞪大了眼睛，好像发现了新大陆一样，大声说：“老师，我好像懂了！”这一嗓子，把其他同学也都给带动起来了，大家纷纷开始积极思考，互相讨论。

讲完这个例子，我又给他们出了几道练习题，让他们自己动手试试。

有的同学一开始还不太熟练，算错了好几遍，但还是不放弃，一直在那琢磨。

等到下课的时候，大部分同学都能掌握这个公式的基本用法了。

看着他们一个个充满成就感的表情，我心里也特别开心。

其实呀，学习梅森公式就像搭积木，一块一块地往上加，只要每一步都踏实，最后就能搭出漂亮的城堡。

不管是在数学里，还是在生活中，很多事情都是这样，看起来很难，但只要我们有耐心，有方法，总能把难题给解决掉。

所以呀，别害怕梅森公式，勇敢地去探索它，说不定你会发现其中的乐趣呢！。

matlab梅森公式梅森公式，也称为梅森素数公式（Mersenne prime），是描述素数形式的一个公式，由法国数学家梅森（Marin Mersenne）在17世纪提出。

梅森公式可以按照以下形式表示：M = 2^p -1其中，M为梅森素数，p为素数。

梅森公式是一种简洁而有效的表达方式，可以很方便地生成梅森素数。

梅森素数是指满足梅森公式的素数。

例如，当p取2、3、5、7、13等值时，可以得到对应的梅森素数：3、7、31、127、8191等。

梅森素数在数论和计算机科学中有着重要的应用。

其中最为著名的应用之一就是在密码学领域。

RSA公钥加密算法中的素数选择和密钥生成就依赖于梅森素数。

此外，梅森素数还被广泛应用于快速傅里叶变换（FFT）和伪随机数生成等领域。

在数字计算中，梅森素数也用于帮助加快素数的测试和计算。

梅森素数的研究一直是数学家们的热点之一。

目前已知的梅森素数很少，大部分梅森素数都是通过计算机程序来生成的。

由于梅森公式的形式简单，计算机可以更快速地验证一个数是否是梅森素数。

但是这并不意味着每个满足梅森公式的数都是素数，只是方便验证。

在数学研究中，确定梅森素数的性质一直是一个重要的课题。

目前已知的梅森素数都是奇数，但是否所有的满足梅森公式的奇数都是素数，仍然是一个未解的问题。

数学家们一直在努力寻找更多的梅森素数，并且为梅森素数的性质和规律提供了许多重要的定理和猜想。

在实际计算中，由于梅森素数的位数非常大，大于几百甚至上千位，因此对梅森素数的计算和验证需要使用高效的算法和计算工具。

MATLAB是一种功能强大的数值计算和编程软件，可以用于计算和验证梅森素数。

MATLAB提供了丰富的数值计算库和函数，可以方便地进行大整数运算和素性测试，帮助研究人员寻找和验证梅森素数。

总之，梅森公式是描述素数形式的一种简洁有效的公式，可以方便地生成梅森素数。

梅森素数在密码学、计算机科学和数学研究中有着重要的应用。

通过使用MATLAB等计算工具，数学家们可以更方便地计算和验证梅森素数，推动梅森素数的研究和应用。

例1:只有一条前向通路 6543211G G G G G G p = 共有4个单回路：n 4i i1234i 1i 11234561232453344L LL L L L G G G G G G H G G H G G H G G H ====+++=----∑∑只有II 、III 两个回路不接触：L L L H H G G G G )H G G )(H G G (L L L L kji32543235423232j i ==--==∑∑∑3254324433542321654321j i i H H G G G G H G G H G G H G G H G G G G G G 1L L L -1 +++++=+=∆∴∑∑所有回路均与之接触11=∆325432443354232165432165432111H H G G G G H G G H G G H G G H G G G G G G 1G G G G G G p )(s +++++=∆∆=Φ∴ 例2: 有五个回路：4124232121321iji4124232121321i G G HG H G G H G G G G G 1L 10L L GG H G H G G H G G G G G L +++++=-=∆=-----=∑∑∑两条前向通路：412423212132141321221124121 3211G G H G H G G H G G G G G 1G G G G G p p (s) 1; G G p 1; G G G p ++++++=∆∆+∆=Φ∴=∆==∆=例3:有五个单回路：并且CRs5L CRs1L L L i 521-=∴-====∑可找出六组两两互不接触的回路：Ⅰ-Ⅱ; Ⅰ-Ⅲ;Ⅰ-Ⅴ; Ⅱ-Ⅲ; Ⅲ-Ⅳ; Ⅳ-Ⅴ2j i )CRs (6)CRs1)(CRs 1.(6L L =--=∴∑有一组三个互不接触回路Ⅰ-Ⅱ-Ⅲ333222k j i j i i 3333k j i sR C 1s R C 6CRs 51L L L L L L 1 sR C 1)CRs 1(L L L ∑∑∑∑+++=-+-=∆∴-=-=∴前向通路一条： 1 ; sR C 1p 13331=∆=3C 11R 23321U (s)p (CRs) (s)U (s)1CRs (CRs)(CRs)1(CRs)5(CRs)6CRs 1∆∴Φ===∆+++=+++例4:回路4个：333212211i H G H G G H G H G L --+-=∑ 两两不接触回路两个：Ⅰ-Ⅱ， Ⅱ-ⅣL L L )H G )(H (G )H )(G H G (L L kji33222211j i =-+-=∑∑32322121333212211H H G G H H G G H G H G G H G H G 1 --++-+=∆∴前向通道两条：32322121333212211223212211222321211H H G G H H G G H G H G G H G H G 1)H G -(1G G G p p (s) H G -1; G p 1; G G p --++-++=∆∆+∆=Φ∴=∆==∆=例5 已知系统结构图，求?)s (R )s (C =解：本结构图有2条前向通道，6个回路(其中I ，V 两回路不相交)H G G G G G H 1H)(1 G G G (s) H 1; G p 1; G G p H G G G G G H 1 )H )].(G ([)]}G ([)G (G G G G H {1321123212321211321123332112-+++++-=Φ∴+=∆-==∆=-++++=---+----------=∆例6 求?)s (R )s (C =解：共有3个单回路(全部有公共接触部分)H G H G G G H G G G G 1 L 1Δ HG H G G G H G G G G L L 2214211432131i i 2214211432131i i i-++=-=∴+--==∑∑∑==前向通道共有6条：1 G G G G p 143211=∆=1 G G G p 24212=∆= 1 G G G G p 343253=∆= 1 G G G p 44254=∆= 1 G G G p 54365=∆-= 1 G G H G p 642266=∆-= G H G G G H G G G G 142114321+-由梅逊公式：2214211432142264364254325421432166554433221161i iiH G H G G G H G G G G 1G G H G G G G G G G G G G G G G G G G G G Δp Δp Δp Δp Δp Δp Δp )s (-++--+++=∆+++++=∆=Φ∑= 例7 已知系统结构图 1).画出系统信号流图 2).求(s)R C(s),(s)R C(s)21解：1).2).)II I,.(3.2:C R .:C R 21互不相交其中个回路共有条前向通道有有3条前向通道⎭⎬⎫→→{}4321321432143211324321G G G G G G G G G G G 1 )G G G )(G ()G G G (G G G G 1+-++=--+-----=∆1G G G G p 1 G G G p G G G 1 G p :C R 343213232124321111=∆-==∆-=+=∆=→1G G p G 1 G G G p :C R 23221143212=∆=+=∆=→∆-=+-++--+=∴321143213214321432132143211G G G G G G G G G G G G G G G 1G G G G G G G )G G G (1G )s (R C(s) 432132143213214322G G G G G G G G G G G 1G G )G (1G G G )s (R C(s)+-++++= 例6 求?)()(=s R s C ?)()(=s N s C 解：431214332212143121433221211))((][1H H H G G H H H H G H G G H H H G G H H H H G H G G ++++--+----=∆　＝对R(s)：∆+=∴--=∆=)1()()()(1;4321431211H H G G s R s C H H G G P 对N(s)：∆∆∆)1)(()()()(1;)(1;P 4332432214313n1H H G G s N s C H H G P H H G n n n ++=∴--==--== 例7 求?)(/)(=s R s C解：212121211))((][1G G G G G G G G +++=--+---=∆ 1;1211==∆ G G P )(1;12322G G G P --==∆ ∆∆=+---==2121333][1;G G G G G P ∆∆⋅+++=∴313221)1()()(G G G G G G s R s C例8 求?)()(=s R s C 解：][121122121G G G G G G G G -----=∆1111=-=∆ G P 1222==∆ G P 1))((3213=--=∆ G G P 14124==∆ G G P 21212121212112212131231)()(G G G G G G G G G G G G G G G G G G s R s C ++-++-=++-+++-=∴。

matlab 梅森公式MATLAB 梅森公式梅森素数•梅森数是指形如2^p-1的整数，其中p是一个素数。

即梅森数可以表示为M_p = 2^p - 1。

•素数是指只能被1和自身整除的整数，且大于1。

梅森公式•梅森公式用于判断一个数是否是梅森素数，公式为：2^p - 1是素数当且仅当p是素数MATLAB代码function isMersenne = isMersennePrime(p)% 判断一个数是否是梅森素数% 输入：p - 待判断的数% 输出：isMersenne - 判断结果，是梅森素数返回true，否则返回false% 判断p是否为素数if isprime(p)% 计算Mersenne数mersenneNum = 2^p - 1;% 判断Mersenne数是否为素数isMersenne = isprime(mersenneNum);elseisMersenne = false;endend示例说明isMersennePrime(2)•该示例调用isMersennePrime函数，输入参数为2。

•根据梅森公式，计算2^2-1=3。

•判断3是否为素数，结果为true。

•返回结果为true，说明2是梅森素数。

isMersennePrime(10)•该示例调用isMersennePrime函数，输入参数为10。

•根据梅森公式，计算2^10-1=1023。

•判断1023是否为素数，结果为false。

•返回结果为false，说明10不是梅森素数。

梅森素数的性质•梅森素数具有一些特殊的性质，使得它们在数论和计算机科学中有着重要的应用。

性质1：梅森素数的指数必须也是素数•根据梅森公式，如果一个数是梅森素数，那么它的指数必须也是素数。

•假设一个数是梅森素数，但其指数不是素数，那么根据梅森公式，梅森数也不会是素数。

•因此，这个性质确保了梅森素数的指数和梅森数必须同时为素数。

性质2：梅森素数的指数和梅森数是完美数的一部分•完美数是指它的所有真因数之和等于它本身的数。

梅森增益公式范文Menson Gain FormulaThe Menson Gain Formula is a mathematical formula used in electrical engineering to calculate the power gain of an amplifier. It was developed by British engineer John Menson in the 1950s. The formula is used to calculate the voltage gain of an amplifier, which is the ratio of output voltage to input voltage.The Menson Gain Formula is expressed as follows:Gain = Vo/ViWhere,Gain is the power gain of the amplifier,Vo is the output voltage of the amplifier, andVi is the input voltage to the amplifier.The formula takes into consideration the voltage gain of the amplifier, as well as any losses due to transmission or other factors. By using the formula, engineers can accurately determine how much power is being transferred between the input and output of an amplifier, and what the effects of losses or other factors will be on the overall gain.In addition to its use in the design of electrical and electronic systems, the Menson Gain Formula is also used in theanalysis of acoustic systems. By using the formula, engineers are able to accurately determine the power gain of a speaker or other acoustic system, allowing them to make any necessary adjustments before constructing the system.The Menson Gain Formula is an invaluable tool for engineers who design and build electrical and electronic systems, providing them with the ability to accurately calculate the power gain of amplifiers, circuits, or systems. It is widely used in electrical engineering and audio engineering, as well as other disciplines, and is an important part of the design process.。