2.4 梅森公式

梅森公式求传递函数
梅森公式是一种常用的求解数字滤波器传递函数的方法。

数字滤波器是一种用于数字信号处理的滤波器，其传递函数描述了滤波器对输入信号的影响。

梅森公式可以用于求解各种类型的数字滤波器的传递函数，包括低通、高通、带通和带阻滤波器。

梅森公式的基本形式为：
H(z) = B(z) / A(z)
其中，B(z)和A(z)分别为数字滤波器的分子和分母多项式。

通过对分子和分母多项式进行系数的选择和取值，可以得到不同类型的数字滤波器传递函数。

例如，对于一个二阶低通数字滤波器，其分母多项式可以表示为： A(z) = 1 + a1*z^-1 + a2*z^-2
其中，a1和a2为系数。

通过选择合适的系数值，可以得到所需的滤波器响应特性。

类似地，分子多项式可以表示为：
B(z) = b0 + b1*z^-1 + b2*z^-2
也需要根据需要的响应特性进行系数的选择。

将分子和分母多项式代入梅森公式，即可求得数字滤波器的传递函数。

需要注意的是，在使用梅森公式求解数字滤波器传递函数时，需要考虑数字滤波器的采样率、截止频率等参数，以确保所得到的传递函数具有所需的滤波性能。

同时，由于数字滤波器的传递函数是离散的，因此在实际应用中需要进行数字信号的抽样和插值等处理，以确保信号处理的准确性和精度。

梅森公式
1. 简介
梅森公式（Mersenne formula），是指由法国数学家梅森（Marin Mersenne）在17世纪提出的一种用于生成素数的公式。

梅森公式的基本形式为2^n - 1，其中n是一个自然数。

如果2^n - 1是一个素数，则称之为梅森素数。

梅森公式产生的素数被广泛应用在密码学、计算机科学、通信领域等。

由于其计算简单、结构规律清晰，梅森公式较早被发现，至今为止已知的最大梅森素数为2^82,589,933 - 1。

本文将介绍梅森公式的原理、应用以及一些相关的数学定理。

2. 梅森公式的原理
梅森公式是基于二进制表示的思想，通过将2的幂次方相减得到一个整数，并判断该整数是否为素数。

其基本形式为：
M(n) = 2^n - 1
其中，M(n)为梅森素数。

梅森公式的原理是因为2^n - 1可以通过一种高效的算法进行计算，被称为。

梅森公式经典例题摘要：一、梅森公式简介二、梅森公式经典例题解析1.基本形式2.乘积形式3.复合形式4.应用场景三、梅森公式在实际问题中的应用四、总结与拓展正文：一、梅森公式简介梅森公式（Mason"s formula）是一种在概率论和统计学中广泛应用的公式，用于计算离散随机变量概率密度函数的积分。

梅森公式以数学家梅森（Mason）的名字命名，其一般形式如下：若离散随机变量X有n个可能的结果，对应的概率分别为p1, p2, ..., pn，则X的概率密度函数F(x)可以通过梅森公式计算：F(x) = Σ[pi * (1 - p1^(n-i))]二、梅森公式经典例题解析1.基本形式例题1：已知离散随机变量X有3个可能的结果，分别对应的概率为1/3，1/4，1/5。

求X的概率密度函数。

解：根据梅森公式，计算得到：F(x) = (1/3) * (1 - 1/3^2) + (1/4) * (1 - 1/4^2) + (1/5) * (1 - 1/5^2)2.乘积形式例题2：已知离散随机变量X有2个可能的结果，分别为A和B，对应的概率分别为1/2和1/3。

若事件A和事件B互斥，求X的概率密度函数。

解：根据梅森公式，计算得到：F(x) = (1/2) * (1 - 1/2^2) * (1 - 1/3^2)3.复合形式例题3：已知离散随机变量X有两个可能的结果A和B，对应的概率分别为1/2和1/3。

若随机变量Y = X + 1，求Y的概率密度函数。

解：根据梅森公式，计算得到：F(y) = (1/2) * (1 - 1/2^2) * (1 - 1/(y-1)^2)4.应用场景梅森公式在概率论和统计学中有广泛的应用，例如计算离散随机变量的累积分布函数、概率密度函数等。

此外，梅森公式还可以用于求解马尔可夫链、泊松分布等问题。

三、梅森公式在实际问题中的应用在实际问题中，梅森公式可以用于解决各种概率论和统计学问题。

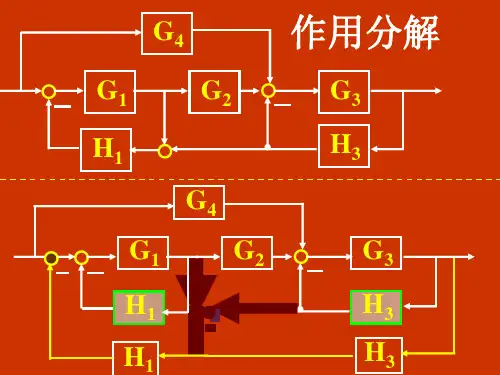
是包含于，你理解的有点偏差，举个例子如果有三个互不接触的回路，取两个不接触的回路应有三项，取三个互不接触回路就一项。

具体的应该是这样：
梅森公式G(s)=Σ(Ρκ*△κ)╱△G(s)= ——系统总传递函数；n——是前向通道数；Ρκ——第k条前向通路的传递函数，由输入端单向传递至输出端的信号通道称为前向通道；△——流图的特征式△=1-ΣLi+ΣLjLk-ΣLiLjLk+······
L A
bc为每两个不接触回路增益乘积之和
a为所有回路增益之和；L a L b
Li——所有单独回路的增益之和；
LjLk——所有互不接触的单独回路中，取其中两个不接触的回路增益乘积之和；LiLjLk——所有互不接触的单独回路中，取三个互不接触回路增益之和；
△κ——第k条前向通路特征式的余因子，即对于流图的特征式△，将与第k 条前向通路相接触的回路
增益代以零值，余下的即为△κ。

对于复杂的结构，理论上有很多项，但实际上△就取到前两三项。

第2章　控制系统的数学模型３１㊀2 4 1　信号流图信号流图是由节点和支路组成的一种信号传递网络图,可以由微分方程组绘制,也可以由结构图转化而来.如图２３６所示为简单的结构图与信号流图之间的转换,变换中,将结　图236　结构图与信号流图之间的转换构图中的输入量㊁输出量变为节点,以小圆圈表示;连接两个节点的定向线段,称为支路;将结构图中的方框去掉,传递函数标在支路的旁边表示支路增益;支路增益表示结构图中两个变量的因果关系,因此支路相当于乘法器,即有C ＝G R .由此可见结构图转换为信号流图的规则:将系统的输入量㊁输出量以及中间变量转化为节点;引出点转化为节点;综合点后的变量转化为节点.方框去掉,将方框的输入量和输出量连起来形成支路.方框中的传递函数标在支路旁边,即为支路增益.　图237　信号流图在信号流图中,常使用以下名词术语.(１)源节点(或输入节点)只有输出支路的节点称为源节点,如图２３７中的R (s )和N (s ).它一般表示系统的输入量.(２)阱节点(或输出节点)只有输入支路的节点称为阱节点,如图２３７中的C (s ).它一般表示系统的输出量.(３)混合节点㊀既有输入支路又有输出支路的节点称为混合节点,如图２３７中的X １㊁X ２㊁X ３.它一般表示系统的中间变量.(４)前向通道信号从源节点到阱节点传递时,每一个节点只通过一次的通道,称为前向通道.前向通道上各支路增益之乘积,称为前向通道总增益,一般用p k 表示.在图２３７中,对于源节点R (s )和阱节点C (s ),有一条前向通道,是R (s )ңX １ңX ２ңX ３ңC (s ),其前向通路总增益为P R ＝a b c ;对于源节点N (s )和阱节点C (s ),是N (s )ңX ２ңX ３ңC (s ),其前向通路总增益为P N ＝f c .(５)单回路如果回路的起点和终点在同一节点,而且信号通过每一个节点不多于一次的闭合通路称为单独回路,简称回路.如果从一个节点开始,只经过一个支路又回到该节点的,称为自回路.回路中所有支路增益之乘积叫回路增益,用L a 表示.在图２３７中共有两个回路,L １＝b e ,L ２＝d .(６)不接触回路如果一信号流图有多个回路,而回路之间没有公共节点,这种回路叫不接触回路.在信号流图中可以有两个或两个以上不接触回路.在图２３７中,有一对不接触回路,L １L ２＝b e d .2 4 2　梅森增益公式在系统的信号流图上,可以用梅森公式直接求出系统的传递函数,由于信号流图和结构图存在着相应的关系,因此梅森公式同样也适用于结构图.。

简易梅森公式好的，以下是为您生成的关于“简易梅森公式”的文章：梅森公式，这玩意儿听起来好像有点高大上，让人摸不着头脑，但其实呀，它就像一个藏在数学城堡里的小秘密，等我们去揭开它的神秘面纱。

我记得有一次给学生们讲梅森公式的时候，那场面可有意思啦。

当时我在黑板上写下了一堆复杂的公式和符号，学生们的眼神从期待瞬间变成了迷茫，一个个小脑袋瓜里估计都在想：“这是啥呀？”我赶紧打住，说：“同学们，别慌，咱们慢慢来。

”然后我就从最基础的概念开始讲起。

咱们先来说说啥是梅森公式。

它呀，其实就是用来计算线性系统传递函数中分母多项式的特征根的个数。

听起来是不是还是有点晕？没关系，咱们举个例子。

比如说有一个系统，它的传递函数分母多项式是 s^3 + 2s^2 + 3s + 4 ，咱们用梅森公式就能很快算出这个多项式有几个根。

那梅森公式到底长啥样呢？它大概是这样的：Pk 表示第 k 条前向通路的传递函数，Δ 表示特征式，Δk 表示第 k 条前向通路特征式的余子式。

哎呀，光说这些公式和概念，估计你们都快睡着了。

咱们还是回到刚刚那个例子。

我当时就一步一步地带着学生们，把每一项都算出来，然后得出最终的结果。

在这个过程中，有个平时挺调皮的学生，突然瞪大了眼睛，好像发现了新大陆一样，大声说：“老师，我好像懂了！”这一嗓子，把其他同学也都给带动起来了，大家纷纷开始积极思考，互相讨论。

讲完这个例子，我又给他们出了几道练习题，让他们自己动手试试。

有的同学一开始还不太熟练，算错了好几遍，但还是不放弃，一直在那琢磨。

等到下课的时候，大部分同学都能掌握这个公式的基本用法了。

看着他们一个个充满成就感的表情，我心里也特别开心。

其实呀，学习梅森公式就像搭积木，一块一块地往上加，只要每一步都踏实，最后就能搭出漂亮的城堡。

不管是在数学里，还是在生活中，很多事情都是这样，看起来很难，但只要我们有耐心，有方法，总能把难题给解决掉。

所以呀，别害怕梅森公式，勇敢地去探索它，说不定你会发现其中的乐趣呢！。

梅森素数梅森素数素数也叫质数，是只能被自己和1整除的数，如2、3、5、7、11等。

2300年前，古希腊数学家欧几里得证明了素数有无穷多个，并提出少量素数可写成“2p-1”的形式，这里的指数p也是一个素数。

由于这种素数具有许多独特的性质和无穷的魅力，千百年来一直吸引着众多的数学家和无数的业余数学爱好者对它进行探究。

可能你还是不太了解，那就再详细点。

了解梅森素数还记得你小学时背诵的素数表吗？那时候它还叫做质数表“2、3、5、7……”如今你是否已经真正理解了老师说过的话：这些只能被1和本身整除的数，具有着无穷的魅力。

还记得你中学时计算的2的整数幂吗？计算机时代，作为二进制的体现，它们正大行其道。

“2、4、8、16、32、64、128、256……”十多年来，电脑内存的容量正是经历了这些熟悉的数字，直到现在的2048M（2G）以及更多。

现在，让我们从这些2的整数幂中挑出以素数为指数的，再把它减1，试试看会发现什么？22－1＝3、23－1＝7、25－1＝31、27－1＝127……嗯，你的心是不是激动起来了？一个伟大的发现似乎就在眼前……别急别急，你的发现很妙，只是有些儿惋惜……你已经迟到了二千年。

在2300多年前，古希腊的数学家，那位写出不朽的《几何原本》的欧几里得在证明了素数有无穷多个之后，就顺便指出：有许多素数可以写成2P－1的形式，其中指数P也是素数。

很容易想到，刚才你所发现的22－1、23－1、25－1、27－1正是其中排列最前的4个！当P＝11、13、17、19、23……的时候，2P－1还是素数吗？到底有多少这种2P－1型的素数呢？在计算能力低下的公元前，这个关于素数的探寻之旅就已经吸引了无数的人。

人们唯独对素数如此着迷不是没有理由的，它有着许多简单而又美丽的猜想，有的已经成为定理，而有的则至今还没有答案。

例如著名的哥德巴赫猜想，让人们苦苦追索：是否任何一个大于或等于6的素数，都可以表示为两个奇素数的和？再比如孪生素数问题所提出的：像5和7、41和43这样相差2的素数，到底有多少对呢？在数学史上起个大早的古希腊人还有许多关于素数的发现，完美数就是其中之一。

梅森公式的特征式梅森公式是一种用于生成伪随机数的算法，它的特征式是一个非常重要的概念。

特征式是指一个矩阵的特征值所满足的方程式，它在计算机科学中有着广泛的应用。

梅森公式是一种伪随机数生成算法，它的原理是通过一个初始值来生成一系列的随机数。

这个初始值被称为种子，它可以是任何整数。

梅森公式的核心是一个线性同余方程，它的形式为：Xn+1 = (aXn + c) mod m其中，Xn是第n个随机数，a、c、m是常数。

这个方程的意思是，下一个随机数等于上一个随机数乘以一个常数再加上另一个常数，然后对一个大的数取模。

这个大的数通常是2的某个次幂，比如2的32次方或2的64次方。

梅森公式的特征式是一个非常重要的概念，它可以用来判断一个伪随机数生成算法的质量。

特征式是一个矩阵的特征值所满足的方程式，它可以用来计算矩阵的特征值。

在梅森公式中，特征式的形式为：X^n - (a1)X^(n-1) - (a2)X^(n-2) - ... - (an-1)X - an = 0其中，X是一个n维向量，a1、a2、...、an-1、an是常数。

这个方程的意思是，矩阵乘以一个向量等于这个向量乘以一个常数。

这个常数就是矩阵的特征值，而向量就是对应的特征向量。

特征式的求解是一个非常复杂的过程，通常需要使用数值计算方法来求解。

在梅森公式中，特征式的求解可以用来判断算法的周期长度和随机性。

周期长度是指生成的随机数序列重复出现的长度，而随机性是指生成的随机数序列的均匀性和无序性。

梅森公式的特征式是一个非常重要的概念，它可以用来判断一个伪随机数生成算法的质量。

特征式的求解是一个非常复杂的过程，但是它可以帮助我们更好地理解伪随机数生成算法的原理和性质。

梅森公式经典例题摘要：一、梅森公式简介1.梅森公式的定义2.梅森公式在数学中的重要性二、经典例题解析1.例题一：利用梅森公式求解2.例题二：利用梅森公式求解3.例题三：利用梅森公式求解三、例题解答与总结1.例题一解答2.例题二解答3.例题三解答4.总结：梅森公式在解题中的应用与技巧正文：一、梅森公式简介梅森公式，又称伯努利公式，是数学领域中一个非常重要的公式。

它是由瑞士数学家雅各布·伯努利（Jacob Bernoulli）提出的，用于描述调和级数的性质。

梅森公式在数学中具有很高的地位，被广泛应用于组合数学、概率论、数论等多个领域。

二、经典例题解析接下来，我们将通过三个经典例题来解析梅森公式在实际问题中的应用。

例题一：利用梅森公式求解题目：已知等差数列的前n 项和为S_n，求S_n^2 与n^3 之间的关系。

解答：根据梅森公式，我们可以得到S_n = n*(2a + (n-1)*d)/2，其中a 为数列的首项，d 为公差。

将S_n 代入S_n^2 中，我们可以得到S_n^2 = n^2*(4a^2 + 4a*d + d^2 + 2a*(n-1)*d)/4。

通过化简，我们可以发现S_n^2 与n^3 之间的关系为S_n^2 = n^2*(2a^2 + 2a*d + d^2)/4 +n^3*(a*d - a^2)/4。

例题二：利用梅森公式求解题目：求解组合数C(n, k) 的梅森公式表示。

解答：根据梅森公式，我们可以得到C(n, k) = n! / (k! * (n-k)!)。

将C(n, k) 的定义代入梅森公式中，我们可以得到C(n, k) = (n*(n-1)*...*(n-k+1)) / (k*(k-1)*...*1)。

进一步化简，我们可以得到C(n, k) = n*(n-1)*...*(n-k+1) / k!。

例题三：利用梅森公式求解题目：已知正整数n，求解1^2 + 2^2 + ...+ n^2 的值。

、 梅森公式(Mason ’s Formula)从系统的信号流图直接求系统函数()()()s F s Y s H =的计算公式，称为梅森公式。

该公式如下：()()()∑∆∆==k kk P 1s F s Y s H (6-34)此公式的证明甚繁，此处略去。

现从应用角度对此公式予以说明。

式中+-+-=∆∑∑∑r,q .p r q p n,m n m iI L L L L L L 1 (6-35)Δ称为信号流图的特征行列式。

式中：i L 为第i 个环路的传输函数， i i L 为所有环路传输函数之和；n m L L 为两个互不接触环路传输函数的乘积，n m L mL 为所有两个互不接触环路传输函数乘积之和；r q p L L L 为三个互不接触环路传输函数的乘积， ∑rq,p,rq p L L L 为所有三个互不接触环路传输函数乘积之和；k P 为由激励节点至所求响应节点的第k 条前向开通路所有支路传输函数的乘积；k ∆为除去第k 条前向通路中所包含的支路和节点后所剩子流图的特征行列式。

求k ∆的公式仍然是式(6-35)。

例6-19 图6-34(a)所示系统。

求系统函数()()()s F s Y s H =。

解：1 求Δ(1) 求∑iiL：该图共有5个环路，其传输函数分别为2L 1=，8,42L 2=⨯=()-11-1L 3=⨯= 2L 4=，()421-2L 5=⨯⨯-=故 ∑iiL15L L L L L 54321=++++=)s ()a ()b图6-34(2) 求 ∑nm,nmL L:该图中两两互不接触的环路共有3组：()1628L L 422L L 212L L 424131=⨯==⨯=-=-⨯=故 18L L L L L L L L424131nm,n m=++=∑该图中没有3个和3个以上互不接触的环路，故有 0LL L rrq,p,qp=∑；…。

故得418151L L L L L L -1r rq,p,q p n,m n m ii =+-=+-+=∆∑∑∑2 求∑∆kkk P(1) 求k P ：该图共有3个前向通路，其传输函数分别为1111P 1=⨯⨯=()-41141-1P 2=⨯⨯⨯⨯= ()()2121-1P 3=⨯-⨯⨯=(2) 求k ∆:除去1P 前向通路中所包含的支路和节点后，所剩子图如图6-34(b)所示。