K1.24 梅森(Mason)公式

mason公式
Mason公式是一种计算投资回报率的常用公式，由英国经济学家约翰·梅森（John Mason）提出。

它最初是为了解决企业投资决策的经济学问题，但现在它也被广泛应用于个人投资决策中。

Mason公式的基本思想是：当投资者从投资中获得的回报率（returns）超过他们支付的税收（taxes）时，他们将获得投资回报。

Mason公式可以用来计算投资的综合回报率（overall return），它可以帮助投资者判断在投资资金的有限情况下，哪种投资行为会带来最大收益。

Mason公式为：
R = [(1-t)R-t]/(1-t)
其中，R表示投资回报率，t表示税收率。

投资者可以使用Mason公式来计算投资的综合回报率，以帮助他们做出投资决策。

例如，假设投资者投资了100万美元，年回报率为10%，税收率为30%。

那么，投资者的投资综合回报率可以按照Mason公式计算为：
R = [(1-0.3)0.1-0.3]/(1-0.3) = 7%
因此，投资者的投资综合回报率为7%。

Mason公式很容易理解，但它也有一些限制，它只能用于计算投资的综合回报率，而不能用于计算未来投资的综合回报率。

此外，它也不能用于计算投资者个人投资的回报率，因为投资者可能会受到不同的税收率的影响。

总的来说，Mason公式是一种有用的工具，可以帮助投资者识别资金有限的情况下最有利可图的投资行为，避免投资失败。

虽然它有一些局限性，但它仍然是投资者最常用的工具之一，因为它可以帮助投资者更好地识别投资回报率的优劣。

梅森公式经典例题摘要：一、梅森公式简介二、梅森公式经典例题解析1.基本形式2.乘积形式3.复合形式4.应用场景三、梅森公式在实际问题中的应用四、总结与拓展正文：一、梅森公式简介梅森公式（Mason"s formula）是一种在概率论和统计学中广泛应用的公式，用于计算离散随机变量概率密度函数的积分。

梅森公式以数学家梅森（Mason）的名字命名，其一般形式如下：若离散随机变量X有n个可能的结果，对应的概率分别为p1, p2, ..., pn，则X的概率密度函数F(x)可以通过梅森公式计算：F(x) = Σ[pi * (1 - p1^(n-i))]二、梅森公式经典例题解析1.基本形式例题1：已知离散随机变量X有3个可能的结果，分别对应的概率为1/3，1/4，1/5。

求X的概率密度函数。

解：根据梅森公式，计算得到：F(x) = (1/3) * (1 - 1/3^2) + (1/4) * (1 - 1/4^2) + (1/5) * (1 - 1/5^2)2.乘积形式例题2：已知离散随机变量X有2个可能的结果，分别为A和B，对应的概率分别为1/2和1/3。

若事件A和事件B互斥，求X的概率密度函数。

解：根据梅森公式，计算得到：F(x) = (1/2) * (1 - 1/2^2) * (1 - 1/3^2)3.复合形式例题3：已知离散随机变量X有两个可能的结果A和B，对应的概率分别为1/2和1/3。

若随机变量Y = X + 1，求Y的概率密度函数。

解：根据梅森公式，计算得到：F(y) = (1/2) * (1 - 1/2^2) * (1 - 1/(y-1)^2)4.应用场景梅森公式在概率论和统计学中有广泛的应用，例如计算离散随机变量的累积分布函数、概率密度函数等。

此外，梅森公式还可以用于求解马尔可夫链、泊松分布等问题。

三、梅森公式在实际问题中的应用在实际问题中，梅森公式可以用于解决各种概率论和统计学问题。

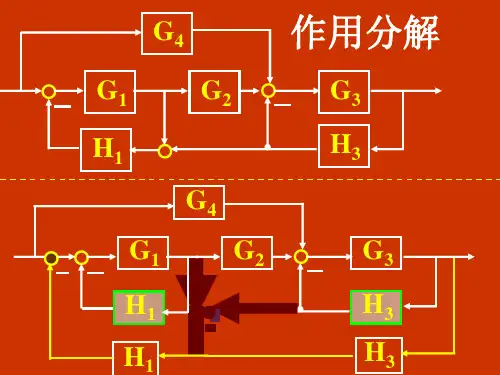
6-5 系统的信号流图与梅森公式一、信号流图的定义由节点与有向支路构成的能表征系统功能与信号流动方向的图，称为系统的信号流图，简称信号流图或流图。

例如，图6-29(a)所示的系统框图，可用图6-29(b)来表示，图(b)即为图(a)的信号流图。

图(b)中的小圆圈“o”代表变量，有向支路代表一个子系统及信号传输(或流动)方向，支路上标注的H(s)代表支路(子系统)的传输函数。

这样，根据图6-29(b)，同样可写出系统各变量之间的关系，即图6-29二、三种运算器的信号流图表示三种运算器：加法器、数乘器、积分器的信号流图表示如表6-3中所列。

由该表中看出：在信号流图中，节点“o”除代表变量外，它还对流入节点的信号具有相加(求和)的作用，如表中第一行中的节点Y(s)即是。

三、模拟图与信号流图的相互转换规则模拟图与信号流图都可用来表示系统，它们两者之间可以相互转换，其规则是：(1) 在转换中，信号流动的方向(即支路方向)及正、负号不能改变。

(2) 模拟图(或框图)中先是“和点”后是“分点”的地方，在信号流图中应画成一个“混合”节点，如图6-30所示。

根据此两图写出的各变量之间的关系式是相同的，即。

(3) 模拟图(或框图)中先是“分点”后是“和点”的地方，在信号流图中应在“分点”与“和点”之间，增加一条传输函数为1的支路，如图6-31所示。

(4) 模拟图(或框图)中的两个“和点”之间，在信号流图中有时要增加一条传输函数为1的支路(若不增加，就会出现环路的接触，此时就必须增加)，但有时则不需增加(若不增加，也不会出现环路的接触，此时即可以不增加。

见例6-17)。

(5) 在模拟图(或框图)中，若激励节点上有反馈信号与输入信号叠加时，在信号流图中，应在激励节点与此“和点”之间增加一条传输函数为1的支路(见例6-17)。

(6) 在模拟图(或框图)中，若响应节点上有反馈信号流出时，在信号流图中，可从响应节点上增加引出一条传输函数为1的支路(也可以不增加，见例6-17)。

梅森公式，求零状态响应梅森公式（Mason's formula）是控制工程中用于求解线性时不变系统传递函数的一种方法，它基于信号流图的分析。

然而，梅森公式本身并不直接用于求解零状态响应，而是用于确定系统的整体传递函数。

零状态响应是指系统在初始状态为零时，对输入信号的响应。

要求零状态响应，通常需要通过以下步骤：1.确定系统的微分方程或差分方程，这通常基于系统的物理特性或电路元件的关系。

2.对微分方程或差分方程进行拉普拉斯变换或Z变换，将时域方程转换为复频域或Z域的代数方程。

3.利用代数方法求解变换后的方程，得到系统的传递函数H(s)或H(z)。

4.对传递函数进行反拉普拉斯变换或反Z变换，将其转换回时域，得到系统的单位冲激响应h(t)或单位样本响应h[n]。

5.最后，通过卷积积分（连续时间系统）或卷积和（离散时间系统）将输入信号f(t)或f[n]与单位冲激响应h(t)或单位样本响应h[n]结合起来，得到零状态响应y(t)或y[n]。

在实际应用中，可能会使用各种工具和软件（如MATLAB）来辅助完成这些计算。

如果你有一个具体的系统描述或信号流图，并且想要使用梅森公式来求解传递函数，进而找到零状态响应，你需要首先根据梅森公式计算出传递函数，然后按照上述步骤找到零状态响应。

请注意，以上步骤是一般性的指导，具体问题可能需要特定的处理方法和技巧。

如果你有具体的系统或问题，请提供更多信息以便给出更准确的指导。

以下是一个实际例子：假设我们有一个简单的RC电路，其微分方程为：(\frac{d}{dt}V(t)+\frac{1}{RC}V(t)=0)其中(V(t))是电压，(R)是电阻，(C)是电容。

1.首先，我们对微分方程进行拉普拉斯变换，得到传递函数(H(s)=\frac{1}{RCs+1})。

2.然后，对传递函数进行反拉普拉斯变换，得到单位冲激响应(h(t)=e^{-\frac{t}{RC}})。

3.假设输入信号是(f(t)=\sin(t))，我们将输入信号和单位冲激响应进行卷积积分，得到零状态响应(y(t)=\int_{0}^{t}e^{-\frac{(t-u)}{RC}}\sin(u)du)。

简易梅森公式好的，以下是为您生成的关于“简易梅森公式”的文章：梅森公式，这玩意儿听起来好像有点高大上，让人摸不着头脑，但其实呀，它就像一个藏在数学城堡里的小秘密，等我们去揭开它的神秘面纱。

我记得有一次给学生们讲梅森公式的时候，那场面可有意思啦。

当时我在黑板上写下了一堆复杂的公式和符号，学生们的眼神从期待瞬间变成了迷茫，一个个小脑袋瓜里估计都在想：“这是啥呀？”我赶紧打住，说：“同学们，别慌，咱们慢慢来。

”然后我就从最基础的概念开始讲起。

咱们先来说说啥是梅森公式。

它呀，其实就是用来计算线性系统传递函数中分母多项式的特征根的个数。

听起来是不是还是有点晕？没关系，咱们举个例子。

比如说有一个系统，它的传递函数分母多项式是 s^3 + 2s^2 + 3s + 4 ，咱们用梅森公式就能很快算出这个多项式有几个根。

那梅森公式到底长啥样呢？它大概是这样的：Pk 表示第 k 条前向通路的传递函数，Δ 表示特征式，Δk 表示第 k 条前向通路特征式的余子式。

哎呀，光说这些公式和概念，估计你们都快睡着了。

咱们还是回到刚刚那个例子。

我当时就一步一步地带着学生们，把每一项都算出来，然后得出最终的结果。

在这个过程中，有个平时挺调皮的学生，突然瞪大了眼睛，好像发现了新大陆一样，大声说：“老师，我好像懂了！”这一嗓子，把其他同学也都给带动起来了，大家纷纷开始积极思考，互相讨论。

讲完这个例子，我又给他们出了几道练习题，让他们自己动手试试。

有的同学一开始还不太熟练，算错了好几遍，但还是不放弃，一直在那琢磨。

等到下课的时候，大部分同学都能掌握这个公式的基本用法了。

看着他们一个个充满成就感的表情，我心里也特别开心。

其实呀，学习梅森公式就像搭积木，一块一块地往上加，只要每一步都踏实，最后就能搭出漂亮的城堡。

不管是在数学里，还是在生活中，很多事情都是这样，看起来很难，但只要我们有耐心，有方法，总能把难题给解决掉。

所以呀，别害怕梅森公式，勇敢地去探索它，说不定你会发现其中的乐趣呢！。

梅森增益公式推导梅森增益公式（Mason's Gain Formula）在控制工程和信号处理领域可是个相当重要的家伙！它能帮助咱们轻松搞定复杂系统的增益计算，可省了不少事儿。

先来说说啥是梅森增益公式。

简单来讲，它就是一个能让咱不费劲地求出系统传递函数（也就是增益）的神奇公式。

这公式长这样：\[G = \frac{1}{\Delta} \sum_{k} P_k \Delta_k\]这里的\(G\)就是系统的总增益啦，\(\Delta\)是特征式，\(P_k\)是第\(k\)条前向通路的增益，\(\Delta_k\)是第\(k\)条前向通路的余子式。

要推导这个公式，咱们得先从系统的信号流图入手。

信号流图就像是系统的“路线图”，能清晰地展示各个信号之间的关系。

比如说，咱们假设有个简单的系统，就像一个小工厂的生产线。

这个生产线有几个环节，每个环节对产品的处理就像是对信号的加工。

有的环节会让产品变得更好（增益为正），有的环节可能会让产品有点小瑕疵（增益为负）。

咱们先看看前向通路。

前向通路就像是生产线上的一条“直达通道”，从输入直接到输出，中间没有任何回头路或者岔路口。

计算每条前向通路的增益\(P_k\)相对来说还算简单，就是把这条路上各个环节的增益乘起来就行。

接下来是特征式\(\Delta\)。

这玩意儿可有点复杂，它得考虑到系统中的所有回路。

回路就像是生产线上绕了一圈又回到原点的小段，会对信号产生反复的影响。

计算特征式的时候，咱们得把每个回路的增益加起来，再减去两两回路乘积之和，再加上三个回路乘积之和，以此类推。

这听起来有点晕乎，但其实就是个规律，多算几次就熟悉了。

再说说余子式\(\Delta_k\)。

它是在去掉与第\(k\)条前向通路有关的节点和支路后，剩下部分的特征式。

咱们通过一个具体的例子来瞅瞅。

假设咱们有个系统，信号流图长成这样：有两个输入节点，三个中间处理节点，一个输出节点。

其中有两条前向通路，还有几个回路。

梅森公式的特征式梅森公式是一种用于生成伪随机数的算法，它的特征式是一个非常重要的概念。

特征式是指一个矩阵的特征值所满足的方程式，它在计算机科学中有着广泛的应用。

梅森公式是一种伪随机数生成算法，它的原理是通过一个初始值来生成一系列的随机数。

这个初始值被称为种子，它可以是任何整数。

梅森公式的核心是一个线性同余方程，它的形式为：Xn+1 = (aXn + c) mod m其中，Xn是第n个随机数，a、c、m是常数。

这个方程的意思是，下一个随机数等于上一个随机数乘以一个常数再加上另一个常数，然后对一个大的数取模。

这个大的数通常是2的某个次幂，比如2的32次方或2的64次方。

梅森公式的特征式是一个非常重要的概念，它可以用来判断一个伪随机数生成算法的质量。

特征式是一个矩阵的特征值所满足的方程式，它可以用来计算矩阵的特征值。

在梅森公式中，特征式的形式为：X^n - (a1)X^(n-1) - (a2)X^(n-2) - ... - (an-1)X - an = 0其中，X是一个n维向量，a1、a2、...、an-1、an是常数。

这个方程的意思是，矩阵乘以一个向量等于这个向量乘以一个常数。

这个常数就是矩阵的特征值，而向量就是对应的特征向量。

特征式的求解是一个非常复杂的过程，通常需要使用数值计算方法来求解。

在梅森公式中，特征式的求解可以用来判断算法的周期长度和随机性。

周期长度是指生成的随机数序列重复出现的长度，而随机性是指生成的随机数序列的均匀性和无序性。

梅森公式的特征式是一个非常重要的概念，它可以用来判断一个伪随机数生成算法的质量。

特征式的求解是一个非常复杂的过程，但是它可以帮助我们更好地理解伪随机数生成算法的原理和性质。

梅森公式求传递函数梅森公式是一种用于计算传递函数的重要工具。

传递函数是用来描述线性时不变系统的输入和输出之间关系的数学模型。

在工程学和物理学等领域，传递函数被广泛应用于分析和设计控制系统、信号处理系统等。

梅森公式是由美国数学家梅森（Mason）于1953年提出的，它提供了一种简单而有效的方法来计算线性时不变系统的传递函数。

梅森公式的基本原理是将系统的输入和输出分解为若干个路径，然后根据路径的特性来计算传递函数。

我们需要明确系统的输入和输出。

输入是指作用于系统的信号，可以是一个电压或电流信号，也可以是一个力或位移信号。

输出是指系统对输入信号的响应，通常也是一个电压或电流信号。

通过对输入和输出进行测量和分析，我们可以得到系统的传递函数。

接下来，我们将输入和输出分解为不同的路径。

路径是指信号从输入到输出的传播路径。

在分解路径时，我们需要考虑信号在系统中的传播方式，例如，信号经过放大器、滤波器、延迟器等部件。

每个路径都可以看作是一个单独的传递函数，它描述了信号在该路径上的传播特性。

然后，我们根据路径的特性来计算传递函数。

对于一个路径，我们可以通过测量信号在该路径上的增益和相位差来确定传递函数。

增益是指信号在路径上的幅度变化，相位差是指信号在路径上的相位变化。

通过测量多个路径的增益和相位差，并将它们组合起来，我们可以得到整个系统的传递函数。

梅森公式的优点在于它提供了一种直观而灵活的方法来计算传递函数。

通过分解路径和测量增益和相位差，我们可以准确地描述系统的传递特性。

此外，梅森公式还可以帮助我们理解系统的结构和性能，从而指导系统的设计和优化。

然而，梅森公式也有一些限制。

首先，它只适用于线性时不变系统，对于非线性或时变系统，梅森公式无法有效计算。

其次，梅森公式假设系统的输入和输出是线性关系，但实际系统中常常存在非线性因素，这可能导致梅森公式的计算结果不准确。

梅森公式是一种重要的工具，用于计算传递函数。

通过分解路径和测量增益和相位差，梅森公式可以帮助我们准确地描述系统的传递特性。

、 梅森公式(Mason ’s Formula)从系统的信号流图直接求系统函数()()()s F s Y s H =的计算公式，称为梅森公式。

该公式如下：()()()∑∆∆==k kk P 1s F s Y s H (6-34)此公式的证明甚繁，此处略去。

现从应用角度对此公式予以说明。

式中+-+-=∆∑∑∑r,q .p r q p n,m n m iI L L L L L L 1 (6-35)Δ称为信号流图的特征行列式。

式中：i L 为第i 个环路的传输函数， i i L 为所有环路传输函数之和；n m L L 为两个互不接触环路传输函数的乘积，n m L mL 为所有两个互不接触环路传输函数乘积之和；r q p L L L 为三个互不接触环路传输函数的乘积， ∑rq,p,rq p L L L 为所有三个互不接触环路传输函数乘积之和；k P 为由激励节点至所求响应节点的第k 条前向开通路所有支路传输函数的乘积；k ∆为除去第k 条前向通路中所包含的支路和节点后所剩子流图的特征行列式。

求k ∆的公式仍然是式(6-35)。

例6-19 图6-34(a)所示系统。

求系统函数()()()s F s Y s H =。

解：1 求Δ(1) 求∑iiL：该图共有5个环路，其传输函数分别为2L 1=，8,42L 2=⨯=()-11-1L 3=⨯= 2L 4=，()421-2L 5=⨯⨯-=故 ∑iiL15L L L L L 54321=++++=)s ()a ()b图6-34(2) 求 ∑nm,nmL L:该图中两两互不接触的环路共有3组：()1628L L 422L L 212L L 424131=⨯==⨯=-=-⨯=故 18L L L L L L L L424131nm,n m=++=∑该图中没有3个和3个以上互不接触的环路，故有 0LL L rrq,p,qp=∑；…。

故得418151L L L L L L -1r rq,p,q p n,m n m ii =+-=+-+=∆∑∑∑2 求∑∆kkk P(1) 求k P ：该图共有3个前向通路，其传输函数分别为1111P 1=⨯⨯=()-41141-1P 2=⨯⨯⨯⨯= ()()2121-1P 3=⨯-⨯⨯=(2) 求k ∆:除去1P 前向通路中所包含的支路和节点后，所剩子图如图6-34(b)所示。

3.梅森公式
对于一个确定的信号流图或方框图，应用梅森公式可以直接求得输入变量到输出变量的系统传递函数。

梅森公式可表示为
（3.78）
式中——系统总传递函数；
——第条前向通路的传递函数；
——流图的特征式
式中——所有不同回路的传递函数之和；
——每两个互不接触回路传递函数乘积之和；
——每三个互不接触回路传递函数乘积之和；
——第条前向通路特征式的余因子，即对于流图的
特征式，将与第条前向通路相接触的回路
传递函数代以零值，余下的即为。

下面通过求图3.48f所示二级电路网络信号流图的传递函数来说明梅森公式的用法。

这个系统中，输入变量与输出变量之间只有一条前向通道，其传递函数为
信号流图里有三个不同回路，它们的传递函数分别为
回路不接触回路（回路接触回路，并且回路接触回路），因此，流图特征式为
（3.79）
从中将与通道接触的回路传递函数、和都代以零值，即可获得余因子。

因此，得到
所以
（3.80）
将式（3.79）和式（3.80）代入式（3.78）便可得到二级电路网络的系统传递函数，即。

一阶回路和二阶回路梅森公式一阶回路和二阶回路是电气工程中常见的电路结构，它们在电路设计和分析中起着重要的作用。

在电路分析过程中，梅森公式是一种常用的方法，能够帮助工程师快速准确地求解复杂电路的参数。

本文将分别介绍一阶回路和二阶回路的基本特点，并深入探讨梅森公式的原理和应用。

一阶回路是指电路中只含有一个电感或一个电容，通常由一个电源、一个电感和一个电阻组成。

一阶回路的特点是响应速度较快，能够满足许多实际应用的要求。

在一阶回路中，电流和电压的关系可以通过简单的微分方程描述，因此可以比较容易地进行分析和计算。

二阶回路则包含两个电感或两个电容，通常由一个电源、两个电感和一个电阻组成。

二阶回路的特点是响应速度较慢，对频率的变化比较敏感，因此在设计中需要特别注意频率特性的影响。

在二阶回路中，电流和电压的关系可以通过二阶微分方程描述，需要更复杂的分析方法来求解。

梅森公式是一种基于网络理论的分析方法，适用于任意复杂的电路。

它是由美国电气工程师理查德·梅森在20世纪40年代提出的，被广泛应用于电路分析和设计中。

梅森公式的核心思想是将复杂的电路网络分解为若干简单的回路，然后通过对各个回路的电压和电流进行叠加，得到整个电路的参数。

在应用梅森公式进行电路分析时，需要按照以下步骤进行：1. 确定电路的节点和支路，画出电路拓扑图；2. 根据拓扑图分解出各个回路，并确定各个回路的电压和电流；3. 根据梅森公式的叠加原理，将各个回路的电压和电流进行叠加，得到整个电路的参数；4. 根据得到的参数，进行电路的分析和设计。

通过梅森公式，工程师可以快速准确地求解复杂电路的参数，帮助他们在电路设计和分析中取得更好的效果。

梅森公式的应用还能够帮助工程师更好地理解电路的工作原理，为他们的工作提供有力的支持。

一阶回路和二阶回路以及梅森公式在电路分析和设计中发挥着重要作用。

工程师在实际工作中，应根据电路的实际情况选择合适的分析方法，并根据具体的情况进行相应的分析和计算。

梅森公式简介梅森公式是用来判断一个自然数是否为梅森数的公式。

梅森数是指形如2^p - 1的素数，其中p是一个自然数。

梅森公式可以用来生成梅森数，并且能够高效地验证一个给定的梅森数是否为素数。

梅森数的生成梅森数的生成基于梅森公式。

根据梅森公式，如果一个数p是素数，那么2^p - 1也是一个梅森数。

这个公式由法国数学家梅森（Marin Mersenne）在17世纪提出。

下面给出一个例子来说明梅森数的生成过程。

假设我们要生成第n个梅森数。

首先，我们需要找到第n个素数p。

我们可以使用素数生成算法来生成素数序列，并取第n个素数作为p的值。

接下来，我们使用梅森公式计算得到梅森数M，即M =2^p - 1。

这个过程可以简化为对2进行p次幂运算，然后减去1得到最终的梅森数。

验证梅森数的素性验证一个给定的梅森数是否为素数是一个关键的问题。

传统的素数测试算法在验证大数是否为素数时效率较低，而梅森公式给出了一种高效的验证方法。

根据梅森公式，如果一个梅森数M是素数，那么对于所有小于M的素数q，满足以下条件：2^q ≡ 1 (mod M)。

这个条件可以用来验证一个梅森数的素性。

具体的验证过程如下：1.首先，选择一个小于M的素数q（通常选择q为M的因子）。

2.计算2^q (mod M)的值。

3.如果计算得到的值等于1，那么继续选择下一个小于M的素数q进行计算。

若计算得到的值不等于1，说明M不是素数。

4.如果所有小于M的素数都满足2^q ≡ 1 (mod M)，那么M就是一个素数。

由于梅森数是形如2^p - 1的数，所以可以利用快速幂算法来高效地计算2^q (mod M)的值。

这样，通过选择合适的q和运用快速幂算法，可以在较短的时间内验证一个梅森数的素性。

应用和发展梅森数及其相关的梅森公式在数论和密码学中具有重要的应用和研究价值。

梅森数作为一类特殊的素数，具有较大的数值和特殊的性质，因此在数论研究中具有重要的地位。

梅森数也广泛应用于密码学领域，例如在RSA公钥加密算法中，使用了素数p和q的梅森数形式来增强算法的安全性。

梅森公式中的特征式
梅森公式是一类素数的公式表达式，由法国数学家梅森提出。

其中的特征式是指在梅森公式中的一个参数，用来判断素数的个数。

具体来说，梅森公式的一般形式为2^n-1，其中n为自然数，若2^n-1为素数，则称2^n-1为梅森素数。

而特征式则是指n值为多少时，2^n-1成为梅森素数。

目前已知的梅森素数只有47个，最大的一个是2^82,589,933-1，共有24,862,048位。

而对于特征式，已知的最大值是
n=82589933。

研究梅森公式和特征式的意义在于探索素数的规律和性质，以及推动密码学和计算机科学等领域的发展。

同时，也需要注意到梅森公式并不是求解素数的唯一方法，仍需进一步研究和发展其他方法。

- 1 -。