当前位置：文档之家 › 系统结构图及等效变换梅森公式

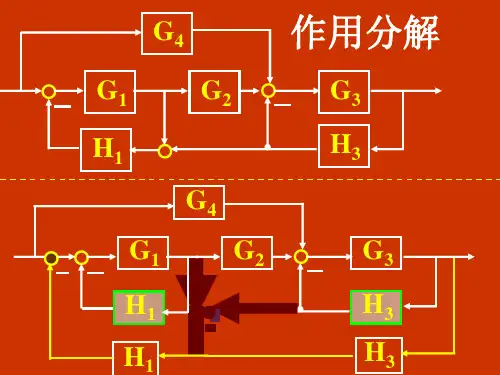
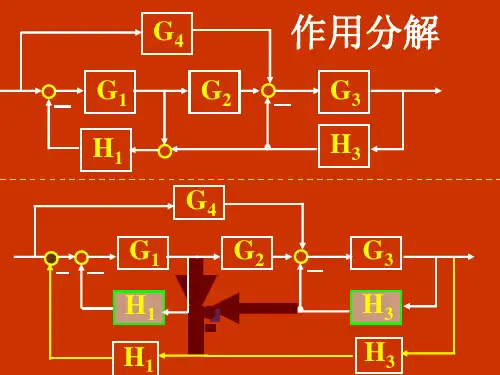
系统结构图及等效变换梅森公式

  • 格式：ppt
  • 大小：2.63 MB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

梅逊公式

梅逊公式

回章首
回节首
21
解: 有三条前向通路， 前向通路的增益分别为
n3
p1 G1G2 G3G4 G5 p2 G1G6 G4 G5 p3 G1G2 G7
有四个独立的回路，分别为
L1 G2 G3G4 G5 H 2 L2 G6 G4 G5 H 2
在四个回路中，L3与L4不接触。
L3 G2 G7 H 2 L4 G4 H1
特征式为
1 ( L1 L2 L3 L4 ) L3 L4
回章首 回节首 22
前向通路p1与四个回路均接触，
1 1
前向通路p2与四个回路均接触，
2 1
前向通路p3与回路L4不接触，
L3a L4 ,
a
3 1 L4
闭环传递函数为
Y (s) P 1 ( p11 p2 2 p3 3 ) R( s) p1 p2 p3 (1 L4 ) 1 ( L1 L2 L3 L4 ) L3 L4 G1G2G3G4G5 G1G6G4G5 G1G2G7 (1 G4 H1 ) 1 G2G3G4G5 H 2 G6G4G5 H 2 G2G7 H 2 G4 H1 G2G7 H 2G4 H1
(2-123)
回章首
回节首
18
特征式
的计算公式为
1 La Lb Lc
a b,c
d ,e, f
L
d
Le L f ....
(2-124)
L —所有独立回路增益之和； —所有每两个互不接触回路增益乘积之和； L L —所有每三个互不接触回路增益乘积之和。 L L L

a a

系统结构图及等效变换梅森公式

系统结构图及等效变换梅森公式

第四节 控制系统的结构图及其等效变换
例 画出图所示电路的动态结构图。
R1
+
U1(s)
R2
ur
-
i1
C1
i1-i2
i2
C2
+
uc
-
解：
Ur(s) _
U1(s)
2(s) I1(s) I_ U1(s) 1 1 C1S _ R1
1 R2
I2(s)
1 C2S
UC(s)
UC(s)
第四节 控制系统的结构图及其等效变换
不是串联！ 也不是串联！ C1(s)=R(s)G1(s)
C(s)=C1(s)G2(s) =R(s)G(s)1G2(s) C(s) =G (s)G (s) 等效 G(s)= R 2 (s ) 1 n G(s) =ΠGi (s) n个环节串联 i=1
第四节 控制系统的结构图及其等效变换
(2) 并联
两个环节的并联等效变换：
第四节 控制系统的结构图及其等效变换
（4）综合点和引出点的移动
1) 综合点之间或引出点之间的位置交换
综合点之间交换： 不改变数学关系 引出点之间的交换： b 不改变数学关系
a
±
c b a aa b c
aa ± cb ± bc ± ± ± a a a
综合点与引出点之间不能交换！
第四节 控制系统的结构图及其等效变换
U ( s ) – U ( s ) r c 系统动态结构图由四种基本符号构成： Ur(s)=RI(s)+Uc(s) =I(s)
第四节 控制系统的结构图及其等效变换
绘制动态结构图的一般步骤:
（1）确定系统中各元件或环节的传递函数。 （2）绘出各环节的方框，方框中标出其传 递函数、输入量和输出量。 （3）根据信号在系统中的流向，依次将各 方框连接起来。

控制系统的结构图及其等效变换

控制系统的结构图及其等效变换

2.
通路
沿支路箭头方向穿过各相 连支路的路径。
前向通路
从源节点到阱节点的通路上通过任何节点
不多于一次的通路。前向通路上各支路增益之 乘积，称前向通路总增益，一般用pk表示。
回路
起点与终点重合且通过任何节点不多于一次的
闭合通路。回路中所有支路增益之乘积称为回 路增益，用Lk表示。
不接触回路
相互间没有任何公共节点的回路
反馈通路断开。 系统开环传递函数：前向通道传递函数与反馈通道传 递函数的乘积。
B( s ) Gk ( s) G1 ( s)G2 ( s) H ( s) E (s)
(反馈信号B(s)和偏差信号E (s)之间的传递函数)
系统的开环传递函数
GK (s) G1 (s)G2 (s) H (s)
注：开环传递函数并非指开环控制系统的传递函数， 而是指闭环系统断开反馈点后整个环路的传递函数。
例2.9 简化下图，求出系统的传递函数。
解： 上图是具有交叉连接的结构图。为消除交叉，可采 用比较点、引出点互换的方法处理。 （1）将相加点a移至G2之后
（2）再与b点交换
（3）因 G4与G1G2并联， G3与G2H是负反馈环节
（4）上图两环节串联，函数相乘后得系统的传递函数为
注： ①以上为原系统的闭环传递函数，不是开环系统的传递函数， 而是闭环系统简化的结果； ②分母中不能看成原闭环系统的开环传递函数，闭环系统开 环传递函数应根据定义和具体框图定。
闭环系统的传递函数
反馈控制系统的典型结构 ：
R( s) E (s) G1(s) B(s)
N (s)
G2(s)
C (s)
H(s)
输入量R(s)、干扰量N(s)同时作用于系统

梅森公式-信号流图

梅森公式-信号流图

例4 已知系统信号流图， 解：三个回路
求传递函数 X4/X1及 X2/X1。
L
a
d eg bcg
c
有两个互不接触回路
L L
b
deg
f
则 1 d eg bcg deg
1. X 1 X 4 , p1 aef , p2 abcf 1 1 d , 2 1
x2
(g)
x2
x3
x5 L5 a23a35a52
a12 a23 a34 a45 (1 a44 )a12 a23 a35 P 1 (a23 a32 a23 a34 a42 a44 a23 a34 a52 a23 a35 a52 ) a23 a32 a44 a23 a35 a52 a44
2 1 a44
x3
a42 a12
a44 a34 x4 a35 a52 a45 x5
(a)
a23 x2 a32 x3
x1
(d)
x2
x3
互不接触
L1 a23a32
L12 a23a32a44 L2 a23a34a42
(e) (f)
x2
x4 x4 x5 L3 a44 互不接触 L22 a23a35a52a44 L4 a23a34a45a52
E(s)=
R(s)[ (1+G2H2) + (- G3G2H3) ] + (–G2H3) N(s)
1 - G1H1 + G2H2
+ G1G2H3 -G1H1G2 H2
信号流图
R(s) 1
e
g
a
f
b

第二章 传递函数-梅逊公式

第二章 传递函数-梅逊公式
第二章 自动控制系统的数学模型
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节（无惯性环节）： c(t)=kr(t)
例
传递函数：G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应：R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图： R(S) k/s C(S)
3
传
递
积分调节器：
C
在A点列方程可得：
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC＝T（积分时间常数），则有：Uc(t)=1/T∫Uc(t)dt
拉氏变换后为：Uc(S)=1/(TS)Uc(S)
5）传递函数具有正、负号（输入量和输出量的变化方向）。
6）传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7）传递函数可以写成
G(s)
Kg
j1 n

系统结构图及等效变换、梅森公式

系统结构图及等效变换、梅森公式
统结构图基础上应用等效变换和梅森 公式进行系统设计和实现，确保系统稳定性和可靠性。
05
结论与展望
BIG DATA EMPOWERS TO CREATE A NEW
ERA
研究结论
• 通过分析和比较不同系统结构图的特点和性能，本文得出了一些重要的结论。首先，等效变换在系统分析和设 计中具有重要的作用，它可以帮助我们简化复杂的系统结构，降低分析和设计的难度。其次，梅森公式是一种 有效的系统性能评估方法，它可以用于计算系统的传递函数和频率响应等关键性能指标。最后，通过实例分析 和仿真验证，本文证明了等效变换和梅森公式在系统分析和设计中的有效性和实用性。
案例一
分析一个简单的RC电路，利用梅 森公式计算其传递函数，并与实 验结果进行对比分析。
案例二
针对一个控制系统，利用梅森公 式分析其稳定性，并给出相应的 控制器设计建议。
案例三
考虑一个复杂的信号流图，利用 梅森公式进行化简，得到简化的 数学模型，便于后续分析和设计。
BIG DATA EMPOWERS TO CREATE A NEW ERA
案例分析
案例一
串联等效变换的应用。在某控制系统中，存在两个串联的控制器，通过串联等效变换，可以将这两个控制器 合并为一个等效控制器，从而简化系统分析。
案例二
并联等效变换的应用。在某电力系统中，存在两个并联的电源，通过并联等效变换，可以将这两个电源合并 为一个等效电源，方便进行系统性能评估。
案例三
反馈等效变换的应用。在某通信系统中，存在一个反馈环节，通过反馈等效变换，可以将该反馈环节进行简 化，使得简化后的系统与原系统在性能上保持一致。
系统结构图及等效变换、
BIG DATA EMPOWERS TO CREATE A NEW

自动控制原理第二章梅森公式-信号流图课件

自动控制原理第二章梅森公式-信号流图课件

ABCD
然后，通过分析梅森公式 的各项系数，确定系统的 极点和零点。
最后，将梅森公式的分析 结果转换为信号流图，进 一步明确系统各变量之间 的传递关系。
梅森公式在信号流图中的应用实例
假设一个控制系统的传递函数为 (G(s) = frac{s^2 + 2s + 5}{s^2 + 3s + 2})
在信号流图中，将极点和零点表示为相 应的节点，并根据梅森公式的各项系数 确定各节点之间的传递关系。
02
信号流图基础
信号流图定义与构成
信号流图定义
信号流图是一种用于描述线性动 态系统数学模型的图形表示方法 ，通过节点和支路表示系统中的 信号传递和转换过程。
信号流图构成
信号流图由节点和支路组成，节 点表示系统的动态方程，支路表 示输入输出之间的关系。
信号流图的绘制方法
确定系统动态方程
根据系统描述，列出系统的动态方程。
2
梅森公式与信号流图在描述和分析线性时不变系 统时具有互补性，二者可以相互转换。
3
信号流图能够直观地表示系统各变量之间的传递 关系，而梅森公式则提供了对系统频率特性的分 析手段。
如何使用梅森公式进行信号流图分析
首先，将系统的传递函数 转换为梅森公式的形式。
根据极点和零点的位置， 判断系统的稳定性、频率 响应特性等。
在未来研究中的可能发展方向
随着科技的不断进步和应用需求的不断变化，控制系统面临着越来越多的 挑战和机遇。
在未来研究中，可以利用梅森公式和信号流图进一步探索复杂系统的分析 和设计方法，提高系统的性能和稳定性。
同时，随着人工智能和大数据技术的应用，可以结合这些技术对控制系统 进行智能化分析和优化设计，提高系统的自适应和学习能力。

自动控制原理 第二章 梅森公式-信号流图

自动控制原理 第二章 梅森公式-信号流图

已知系统信号流图， 例4 已知系统信号流图， 解：三个回路
求传递函数 X4/X1及 X2/X1。 。
∑L
则
a
= − d − eg − bcg
有两个互不接触回路 ∑ Lb Lc = deg
∆ = 1 + d + eg + bcg + deg
f
1. X 1 → X 4 , p1 = aef , p2 = abcf ∆1 = 1 + d , ∆ 2 = 1
G4 G1 H1 G4 G1 H1 H1 G2 G2
作用分解
G3 H3
G3 H3 H3
梅逊公式介绍 R-C :
C(s) = R(s)
∑Pk△k △
其中: 其中
△称为系统特征式 △= 1 - ∑La + ∑LbLc -∑LdLeLf+…
所有单独回路增益之和 所有单独回路增益之和 回路增益 ∑LbLc—所有两两互不接触回路增益乘积之和 —所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和 所有三个互不接触回路增益乘积之和
R(s) 1
e
g
a f
b
c
h
d
C(s)
前向通路两条
四个单独回路， 四个单独回路，两个回路互不接触 ab c d + e d (1 – b g) C(s) = – a – bg – c – R(s) 1 f h e h g f + af c h
信号流图
• 信号流图是由节点和支路组成的一种信号传递网络。 信号流图是由节点和支路组成的一种信号传递网络 是由节点和支路组成的一种信号传递网络。 信号流图的基本性质 基本性质： 信号流图的基本性质： 1) 节点标志系统的变量，节点标志的变量是所有流向该节点信 节点标志系统的变量 标志系统的变量， 号的代数和， 表示； 号的代数和，用“O”表示； 表示 2) 信号在支路上沿箭头单向传递； 信号在支路上沿箭头单向传递 在支路上沿箭头单向传递； 3) 支路相当于乘法器，信号流经支路时，被乘以支路增益而变 支路相当于乘法器 信号流经支路时， 相当于乘法器， 成另一信号； 成另一信号； 4) 对一个给定系统，信号流图不是唯一的。 对一个给定系统，信号流图不是唯一的。 x6 信号流图中常用的名词术语： 信号流图中常用的名词术语： x5 x1 • 源节点（输入节点）： 源节点（输入节点）： x2 x3 x7 I(s) x4 o在源节点上，只有信号输出 在源节点上， 在源节点上 1/R1 1+R1C1s R2 支路而没有信号输入的支路， 支路而没有信号输入的支路， 它一般代表系统的输入变量。 它一般代表系统的输入变量。 -1 •阱节点（输出节点）： 阱节点（ 阱节点 输出节点）： 在阱节点上，只有信号输入的支路而没有信号输出的支路， 在阱节点上，只有信号输入的支路而没有信号输出的支路，它 一般代表系统的输出变量。 一般代表系统的输出变量。

系统的信号流图与梅森公式

系统的信号流图与梅森公式

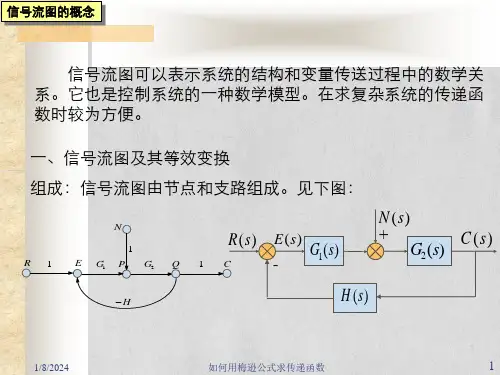
6-5 系统的信号流图与梅森公式一、信号流图的定义由节点与有向支路构成的能表征系统功能与信号流动方向的图，称为系统的信号流图，简称信号流图或流图。

例如，图6-29(a)所示的系统框图，可用图6-29(b)来表示，图(b)即为图(a)的信号流图。

图(b)中的小圆圈“o”代表变量，有向支路代表一个子系统及信号传输(或流动)方向，支路上标注的H(s)代表支路(子系统)的传输函数。

这样，根据图6-29(b)，同样可写出系统各变量之间的关系，即图6-29二、三种运算器的信号流图表示三种运算器：加法器、数乘器、积分器的信号流图表示如表6-3中所列。

由该表中看出：在信号流图中，节点“o”除代表变量外，它还对流入节点的信号具有相加(求和)的作用，如表中第一行中的节点Y(s)即是。

三、模拟图与信号流图的相互转换规则模拟图与信号流图都可用来表示系统，它们两者之间可以相互转换，其规则是：(1) 在转换中，信号流动的方向(即支路方向)及正、负号不能改变。

(2) 模拟图(或框图)中先是“和点”后是“分点”的地方，在信号流图中应画成一个“混合”节点，如图6-30所示。

根据此两图写出的各变量之间的关系式是相同的，即。

(3) 模拟图(或框图)中先是“分点”后是“和点”的地方，在信号流图中应在“分点”与“和点”之间，增加一条传输函数为1的支路，如图6-31所示。

(4) 模拟图(或框图)中的两个“和点”之间，在信号流图中有时要增加一条传输函数为1的支路(若不增加，就会出现环路的接触，此时就必须增加)，但有时则不需增加(若不增加，也不会出现环路的接触，此时即可以不增加。

见例6-17)。

(5) 在模拟图(或框图)中，若激励节点上有反馈信号与输入信号叠加时，在信号流图中，应在激励节点与此“和点”之间增加一条传输函数为1的支路(见例6-17)。

(6) 在模拟图(或框图)中，若响应节点上有反馈信号流出时，在信号流图中，可从响应节点上增加引出一条传输函数为1的支路(也可以不增加，见例6-17)。

如何用梅逊公式求传递函数

如何用梅逊公式求传递函数

• 通路传输(增益)：通路中各支路传输的乘积称为通路传输或通 路增益。前向通路中各支路传输的乘积称为前向通路传输或前 向通路增益。
• 回路传输(增益)：回路上各支路传输的乘积称为回路传输或回
路增益。
1/8/2024
如何用梅逊公式求传递函数
4
信号流图的等效变换
• 串联支路合并：
ab x1 x2 x3
8
例2: 已知结构图如下，可在结构图上标出节点，如上图所示。 然后画出信号流图如下图所示。
k
R(S) b
m
d
V1
l
g V3 e
V2
h
C(S)
f f
m
h
R1
Ⅰ
b
l
Ⅱ
V3
k
Ⅲ
Ⅳ
C
V1 d Ⅴ e V2 1
g
1/8/2024
如何用梅逊公式求传递函数
9
信号流图的绘制
例2: 按微分方程拉氏变换后
的代数方程所表示的变量间
信号流图的概念
信号流图可以表示系统的结构和变量传送过程中的数学关 系。它也是控制系统的一种数学模型。在求复杂系统的传递函 数时较为方便。
一、信号流图及其等效变换
组成：信号流图由节点和支路组成。见下图：
R1
N
1
E G1 P
G2
Q
1
R(s)
C
E(s)
-
G1(s)
N (s)
+ G2(s) C (s)
H
H (s)
式中： La 流图中所有不同回路的回路传输之和；
LbLc 所有互不接触回路中，每次取其中两个回
路传输乘积之和；
LdLeLf 所有互不接触回路中，每次取其中三个

2.7 梅逊公式

2.7 梅逊公式

△1= 1
∑Pk△k= P1△1= G1 G2 G3 G4G5 G6 将中△与第K条前向通道相接触 条前向通道相接触（ △k：将中△与第 条前向通道相接触（有 重合部分）回路所在项去掉之后的余子式。 重合部分）回路所在项去掉之后的余子式。
例：试用梅逊公式求传函C(S)/R(S)。 试用梅逊公式求传函 。
一、梅逊公式
∑Pk△k C(s) : G(S)= R(s) = i G = G1 G3 2 △ 1、G(S)：从输入通道到输出通道总的传递 、 ： H1 H2 H3 函数（总增益）。 函数（总增益）。 2、△：称为系统主特征式 、 △=1- ∑La+ ∑LbLc-∑LdLeLf+…
所有单独回路增益 回路增益之和 ∑La — 所有单独回路增益之和 ∑LbLc—所有两两互不接触回路增益乘积之和 所有两两互不接触回路增益乘积之和 ∑LdLeLf—所有三个互不接触回路增益乘积之和 所有三个互不接触回路增益乘积之和
R G1 G2 1 H2 G3 H4 H1 4 G4 C
2 H3
G5
G6 3
解： 3、G(S) 、
△＝1＋G2G3H2 ＋G4G5H3 ＋G3G4H4 ＋G1G2G3G4G5G6H1＋G2G3G4G5H2 H3
∑Pk△k= P1△1= G1 G2 G3 G4G5 G6 ∑Pk△k C(s) : G(S)= R(s) = i = △
= G1 G2 G3 G4G5 G6
n
△
应用梅逊公式， 应用梅逊公式，将大大简化结构 变换的计算。 变换的计算。但当系统结构较复 杂时，容易将前向通道、 杂时，容易将前向通道、回路数 及余子式判断错，需格外注意。 及余子式判断错，需格外注意。
例：试用梅逊公式求传函C(S)/R(S)。 试用梅逊公式求传函 。 G4 4 G3 2 H2

梅森公式-信号流图

梅森公式-信号流图

L4 a23a34a45a52
x5 L5 a23a35a52
P
a12 a23a34 a45 (1 a44 )a12 a23a35
1 (a23a32 a23a34a42 a44 a23a34a52 a23a35a52 ) a23a32 a44 a23a35a52a44
G3(s)
梅逊公式求E(s)
R(s)
E(SG)GG3(33s(()ss))
RRR(s(()ss)) EEE(S((S)S))
P2= - G3G2H3
GGG1(11s(()ss))
△2= 1 P2△2=?
HHH1(11s(()ss))
G1(s)
NNN((s(ss)))
G2(s)
GGG2(22s(()ss))
CCC(s(()ss))
HHH2(22s(()ss)) H3(s)
HHH3(33s(()ss))
C(s)
R(s)
E(S) P1=H–P1G(s1)2=H13 △△1=11=+G1 2HH2 2(s)P1△1= ?
E(s)= R(s)[ (1+G2H2) +(- G3G2H3)] +(–G2H3)N(s)
1 G1H1 G2G7 H 2 G6G4G5 H 2 G2G3G4G5 H 2 G4G5G7 H1H 2
x1
x2
x3
x7 I(s) x4
x5
o在源节点上，只有信号输出 支路而没有信号输入的支路，
1/R1 1+R1C1s R2
它一般代表系统的输入变量。
-1
•阱节点（输出节点）：
在阱节点上，只有信号输入的支路而没有信号输出的支路，它

第二章2-3系统方框图梅森公式及系统传递函数

第二章2-3系统方框图梅森公式及系统传递函数

? G (s)
综合点后移等效关系图
R(s)

Q(s)
C(s)
G(s)
R(s) G(s)
C(s)

Q(s)
G(s)
综合点前移
R(s)
G(s)
C(s)
Q(s)
R(s)

C(s)
G(s)
？ Q(s)
综合点前移证明推导（移动前）
R(s)
C(s)
G(s)

Q(s)
C(s) R(s) G(s) Q(s)
3
-
-2
H1(s)
?
G3 ( s ) H3(s)
C(s)
G4 ( s )
例2 （解题方法一之步骤3）
R(s)
1
G1(s)
-
G2 ( s )
3
G2 ( s) H 2 ( s )
-
-2
G3 ( s )
H3(s)
H1(s)
C(s)
G4 ( s )
例2 （解题方法一之步骤4）
• 内反馈环节等效变换
1
R(s)
• 内反馈环节等效变换结果
R(s) 1
-
G1 ( s )G2 ( s )
G3 ( s )G4 ( s )
C(s)
1 G2(s)G3(s)H2(s) G3(s)G4(s)H3(s)
两个或两个以上的方框，具有同一个输入信号，并 以各方框输出信号的代数和作为输出信号，这种形
式的连接称为并联连接。
3. 反馈连接
R(s)
－
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后，得 到的输出再返回到这个方框的输入端，构成输 入信号的一部分。这种连接形式称为反馈连接。

自动控制原理 第六课 动态结构图 梅逊公式

自动控制原理 第六课 动态结构图 梅逊公式

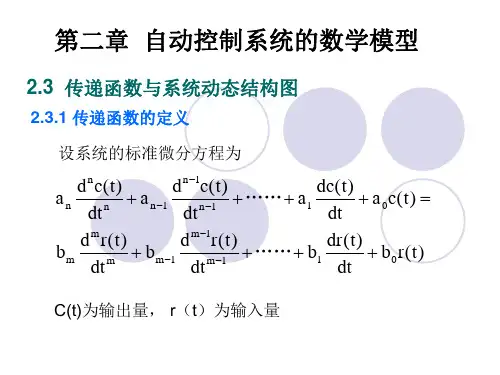
§2-4 传递函数定义控制系统的传递函数为 在零初始条件下 ，输出信号的拉氏变换与输入 信号的拉氏变换之比。

表示为Y ( s ) bm s m + bm -1 s m -1 + ... + b1 s + b0 G( s) = = n , n ³ m (2-95) n -1 U (s) s + a n -1 s + ... + a1 s + a0系统的输出可表示为传递函数与控制输入的乘积Y ( s) = G ( s) × U ( s)(2-96)U(s)G(s)Y(s)回章首回节首12-4-3 控制系统的传递函数 1．复数阻抗U R (s) Z R ( s) = =R I R (s)(2-100)ZC ( s) =UC (s) 1 = I C ( s ) Cs(2-101)U L ( s) Z L ( s) = = Ls I L (s)回章首 回节首(2-102)22．典型环节 (1) 比例环节G(s) = Uo (s) =K Ui (s)(2) 积分环节G( s) = Uo ( s) 1 = Ui ( s) Ts(3) 微分环节U o (s) G (s) = = ts U i (s)3(4) 一阶惯性环节U o ( s) 1 G( s ) = = U i ( s) Ts + 1(5) 二阶振荡环节G( s) = U o ( s) 1 = 2 2 U i ( s ) T s + 2xTs + 1(6) 延迟环节G( s) = U o (s) = e -ts U i ( s)4画结构图时，所依据的原则是信号流通关系。

下面以实例来说明。

[例2-25] 已知两级RC网络如图2-33所示，作出该系 统的结构图。

解 设一个中间变量为电容C1 的电压Ux， 采 用复 数阻抗法顺序写出各 算子代数方程和方块图如下:回章首回节首5(1) U i ( s ) - U x ( s ) = U R1 ( s )(2) U R1 ( s ) × 1 = I ( s) R1(3) I ( s ) - I 2 ( s ) = I1 ( s )( 4) I 1 ( s ) × 1 = U x ( s ) C1 s(5) U x ( s ) - U o ( s ) = U R2 ( s )回章首回节首6(6) U R2 ( s ) × 1 = I 2 ( s ) R2 (7 ) I 2 ( s ) × 1 = U o ( s ) C2 s将各基本环节的方块按照信号流通方向连接起来 就可以得到如图2-33所示的系统方块图。

第二章part-II典型环节结构图梅森公式wmx

第二章part-II典型环节结构图梅森公式wmx

因为v2 v1 0， 所以K 趋向于无穷大。
输出 反相输入 同相输入
补充例4 倒相放大器
解：∵在理想情况下，
i1 0
v2 v1
∴关于节点 v1 的节点方程为：
v1 vin v1 v0 0 R1 R2
输入电流＝输出电流
v2 0
v1 v2 0
vin v0 0 R1 R2 即 v0 R 2 vin R1
G(S ) G1 (S ) G2 (S ) .... Gn (S )
(3)反馈回路传递函数的求取 前向通道：由偏差信号至输出信号的通道； 反馈通道：由输出信号至反馈信号的通道。
Y (S ) G(S ) E (S ) E (S) X(S) - F(S) F(S) H(S)Y(S)
从节点方程中可以得到：
在特殊的情况下， 如果：R2 R1 ， 则：v0 vin 这时，图中的倒相放大器只起到反相的作用。
解： 输入电压与输出电压间的关系为：
按传递函数的定义，可以得到
从图2.11中可以看出，比例环节的特点是：输出信号y(t)和输入信号
x(t)的形状相同。只是比例环节将原信号放大了K倍。
U y ( s)
惯性环节的阶跃响应曲线是 一条指数函数的上升曲线。 从图中可以看出在初始时， 速度的变化最大
惯性环节的阶跃响应曲线
惯性环节的动态方程为一阶微分方程： 将阶跃函数输入 代入方程，求解得到：
y(t ) Kx0 (1 et / T )
在t＝0时刻，初始上升速度为：
Kx0 t / T dy y (0) e dx t 0 T
几个基本概念及术语
R(s)
N(s)
+ -

控制系统的结构图及其等效变换

控制系统的结构图及其等效变换

Y (s)
前移 R1(s) G(s) Y (s)
注：
R2 (s)
R1 ( s )
Y (s)
G(s)
1/G(s) R2 (s)
相加点进入和出去的信号量纲必须相同，否则不能加减。
b引出点（信号由某一点分开）
分支点分出信号，数值相同
R(s) 后移
G(s)
Y (s)
R(s)
R(s) G(s)
Y (s) R(s)
4.比较点（求和点、综合点） 1.用符号“ ”及相应的信号箭头表示 2.箭头前方的“+”或“-”表示加上此信号 或减去此信号
! 注意量纲：相同量纲的物理量
例：二阶RC电气网络
结构图的等效变换和简化
➢系统的结构图通过等效变换和简化后可以方便、快速 地求取闭环系统的传递函数或系统输出量的响应。
➢等效变换和简化的过程对应于消去中间变量求系统传
信号流图的绘制 1. 根据微分方程绘制信号流图 2. 根据方框图绘制信号流图
1. 根据微分方程绘制信号流图
i
A
取Ui(s)、I1(s)、UA(s)、I2(s)、 Uo (s)作为信号流图的节点 Ui(s)、Uo(s)分别为输入及输出节点
2. 根据方框图绘制信号流图
方块图转换为信号流 图
信号流图的等效变换法则
•支路增益——支路传输定量地表明变量从支路一端沿箭头方 向传送到另一端的函数关系。用标在支路旁边的传递函数 “G”表示支路传输。
2.
通路
沿支路箭头方向穿过各相 连支路的路径。
前向通路 从源节点到阱节点的通路上通过任何节点 不多于一次的通路。前向通路上各支路增益之 乘积，称前向通路总增益，一般用pk表示。
信号流图梅森公式

梅逊公式

梅逊公式

2-7 结构图等效变换及梅逊公式求传递函数时，需要对微分方程组（或变换方程组）进行消元，最后仅剩下输入、输出两个变量，因此中间变量的传递过程得不到反映。

若采用结构图，它就能形象地表明输入信号在系统或元件中的传递过程。

另外，下面将会看到，利用结构图，也便于求取传递函数。

所以，结构图在控制理论中应用十分广泛。

一、结构图在第2-6节中，我们曾采用消元法求得图2-24所示RC 网络的传递函数。

这里，我们采用结构图的方法求其传递函数。

RC 网络的微分方程组如下：⎪⎩⎪⎨⎧=+=⎰idt C u u Ri u c cr 1对上两式进行拉氏变换，得)()()(s U s RI s U c r +=或[])()()(1s I s U s U Rc r =- （2-54） )(1)(s I Css U r =（2-55）方程（2-54）可用图2-29)(a 表示，方程（2-55）可用图2-29)(b 表示。

将图2-29)(a )(b 按信号传递方向结合起来，网络的输入量置于图示的左端，输出量置于最右端，并将同一变量的信号连在一起，如图2-30)(a 所示，即得RC 网络结构图。

对图2-30)(a 进行所谓“等效变换”就可得出网络传递函数，因此网络结构就更为简单,如图2-30)(b 所示。

关于结构图等效变换的方法将另作介绍。

（1）建立控制系统各元、部件的微分方程。

（2）对各元、部件的微分方程进行拉氏变换，并做出各元、部件的结构图。

（3）按系统中各信号的传递顺序，依次将各元件结构图连接起来，便得到系统的结构图。

下面以图1-7所示随动系统为例。

把组成该系统各元部件的微分方程（2-18）进行拉氏变换，可得方程组（2-56e a ~），其中比较元件 )()()(s s s c r θθθε-=（2-56a ） 电位器 )()(1s K s U εεθ= （2-56b ） 放大器 )()(2s U k s U ε=（2-56c ） 电动机 )()()1(s U K s s T s m m =+εθ（2-56d ） 减速器)(1)(s is c θθ=（2-56e ）各元、部件的结构图如图2-31所示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章 自动控制系统的数学模型
第二章 总 结
自动控制 解析法 建立微分 拉氏变换
系统
方程
系统传递 函数
拉氏变换
建立动态 结构图
等效变换 梅逊公式
Ф(s)=
C(s) R(s)
第三章 第四章 第五章 第六章
时域法 根轨迹法
频率法 性能校正
分析系统 性能
第二章 自动控制系统的数学模型
第五节 反馈控制系统的传递函数
一、系统的开环传递函数 二、系统的闭环传递函数 三、系统的误差传递函数
第五节 反馈控制系统的传递函数
一、系统的开环传递函数
闭环控制 R(s) 系统的典型
结构：
开环传递函数：
E(s)
_ G1(s)
B(s)
U1(s)
UC(s)
第四节 控制系统的结构图及其等效变换
二、 动态结构图的等效变换与化简
系统的动态结构图直观地反映了系统内部各 变量之间的动态关系。将复杂的动态结构图进行 化简可求出传递函数。
1．动态结构图的等效变换
等效变换： 被变换部分的输入量和输出量 之间的数学关系，在变换前后 保持不变。
第四节 控制系统的结构图及其等效变换
G(s)
s)
R(s)
C(s)
G(s)
R(s)
R(s)
C(s) G(s)
R(s)
1 R(s) G(s)
被移动的支路中串入适当R的(s传) 递函数。
第四节 控制系统的结构图及其等效变换
2．梅逊公式
n
梅逊公式： Φ(s)=
Σk=1Pk Δk
Δ
Pk回Σ—路Li传第k—递条函各前数回向：路通道传的递传函递数函之数和。。 函△k数Σ的—回L乘i的路将L积j回内△中—路。前与所两 递向第在两 函通项k互 数道条去不 乘前和掉向相 积之反通后接 之馈道的触 和通相剩回。道接余路触传部的递传 Σ△Li—Lj分特L，z 征—称式所为余有子三式个。互不相接触回路
（1）串联
R(s)
两个F(环s) 节串C联(s) 的R等(s)效变换：
C1(s) C(s)
G1(s)
RG(s2()GsG)11((ss))GC2(1s()s)CG(Gs2()s1)(s)C(s) G2(s)
不是串C联1(s！)=R(s)G1(s也) 不是串联！
C(s)=C1(s)G2(s) =R(s)G(s)1G2(s)
G(s)=
C(s) R(s)
=G1(s)G2(s)
等效
n个环节串联
n
G(s) =Πi=1Gi (s)
第四节 控制系统的结构图及其等效变换
（3）反馈连接
环节的反馈连接等效变换：
R(s) E(s)
C(s)
G(s)
R(s)
G(s)
C(s)
±
B(s)
1±G(s)H(s)
H(s)
根据框图得： E(s)=R(s) +–B(s)
自动控制理论
第二章 自动控制系统的数学模型
第四节 控制系统的结构图及其等效变换
动态结构图是系统数学模型的另一种形 式，它表示出系统中各变量之间的数学关 系及信号的传递过程。
一、建立动态结构图的一般方法
二、动态结构图的等效变换与化简
第四节 控制系统的结构图及其等效变换
一、 建立动态结构图的一般方法
R(s)
C(s)
± G(s)
后移：
F(s)
R(s)
C(s)
G±(s) G(s)±
F(s)
C(s)=[R(s)±F(s)]G(s)
F(s) FG(s()s) C(s)
数学关G系(s)不变！
第四节 控制系统的结构图及其等效变换
3）引出点相对方框的移动
R(s) G(s)
C(s)
C(s)
前移：
R(s)
C(s)
aa±±cb±±bc ±
bc cb
引出点之间的交换： b
aa
不改变数学关系
a
a
aa
综合点与引出点之间不能交换！
第四节 控制系统的结构图及其等效变换
2）综合点相对方框的移动
R(s) G(s)
C(s) ±
前移： R(s)
G±(s)
C(s) G(s)±
F(s)
C(s)=R(s)G(s)±F(s)
C(s)G1(s) F(s)F(s) ±
的传递函数乘积之和。
Δ = 1 – ΣΣ Lii +ΣΣ Li Lj –ΣΣ LLiiLLjjLLzz + ···
第四节 控制系统的结构图及其等效变换
例 系统的动态结构图如图所示，求
闭环传递函数。
R(s)
_ _ G1
_
L1
G4
L4
G2
G3
L2
L5 H2
+ C(s)
H1
L3
解将L1Δ3+：△==GL系、11–1G+PΣ统PG=G12kHΔ11=–有LGG、11i=GG2+△25LHGG11k1个j1GG代3=2+G22回01GG入H32H路3G12L梅G324H，3+逊=+2G+各G–公G1ΣL1G回1G式2G21P4GL=2路2G得Δi34–=L3+2的+传=jGGGGL传1L21递11zGGGG5=递34函4=4+0H+函G–G数24G4H数H：42H为2 2
以电设流一作R为C电路如U图r(s:)
初输始出微：分 ur=Ri+uc -
取方拉程氏组变换综：合i=点c方ddUu框t cc(s)
R
+ 1 I(s)
+
R
1ur
i 引C 出点uc
C-S
信号线-
系系UI统(统rs(动)s动=)态=C态RS结结UI(构cs构()图s+图)U将由c(各四s)变种量基之本UU间符rc((的ss号))R–=数构UI学(成cs()s关：·)C=系1SI(用s)结
E(s)=1±GR((ss))H(s) C (s)=E(s)G(s)
=R(s) +– E(s)G(s)H(s)
RC((ss))=1±GG((ss))H(s) 等效
第四节 控制系统的结构图及其等效变换
（4）综合点和引出点的移动
1) 综合点之间或引出点之间的位置交换
综合点之间交换： 不改变数学关系
a ±
表 组构意示合两图为变表量：示之出U间来r(s的，) 传将U-递c结(s)函构R1数图。I简(s)化C1，SI(可sU) c方(sC)1S便地Uc(求s) 出任
第四节 控制系统的结构图及其等效变换
绘制动态结构图的一般步骤:
（1）确定系统中各元件或环节的传递函数。
（2）绘出各环节的方框，方框中标出其传 递函数、输入量和输出量。
（3）根据信号在系统中的流向，依次将各 方框连接起来。
第四节 控制系统的结构图及其等效变换
例 画出图所示电路的动态结构图。
+
R1
U1(s) R2
+
i1
i2
ur
C1 i1-i2 C2 uc
-
-
解：
Ur(s) _
I1(s) 1
I_2(s) 1
U1(s)
R1
C1S
_
1
1 UC(s)
R2 I2(s) C2S