04-4.2 薄壁圆筒的扭转
- 格式:pdf
- 大小:702.42 KB
- 文档页数:9





第7讲教学方案——扭转时的内力、薄壁圆筒的扭转第 1 页第三章 扭转§3-1 概述工程上的轴是承受扭转变形的典型构件,如图4-1所示的攻丝丝锥,图4-2所示的桥式起重机的传动轴以及齿轮轴等。
扭转有如下特点:1.受力特点:在杆件两端垂直于杆轴线的平面内作用一对大小相等,方向相反的外力偶——扭转力偶。
其相应内力分量称为扭矩。
2.变形特点:横截面绕轴线发生相对转动,出现扭转变形。
若杆件横截面上只存在扭矩一个内力分量,则这种受力形式称为纯扭转。
§3-2 外力偶矩与扭矩的计算 扭矩图1.外力偶矩m如图4-3所示的传动机构,通常外力偶矩m 不是直接给出的,而是通过轴所传递的功率N 和转速n 由下列关系计算得到的。
nN m 9550= (4-1a) 如轴在m 作用下匀速转动φ角,则力偶做功为φm A =,由功率定义ωφm dtd m dt dA N =⋅==。
角速度ω与转速n (单位为转/分,即r/min )。
关系为60/2n πω=(单位为弧度/秒,rad/s )。
由于1kW=1000N ·m/s ,N 千瓦的功率相当于每秒钟作功N W ⨯=1000,单位为N ·m ;而外力偶在1秒钟内所作的功为m n 2m W ⋅=⋅=πω/60 (N ·m )第 3 页由于二者作的功应该相等,则有m n N ⋅=⨯π21000/60由此便得(4-1)式。
式中:N —传递功率(千瓦,kW ) n —转速(r/min )如果传递功率单位是马力(PS),由于1PS=735.5 N ·m/s ,则有nN m 7024=(N ·m ) (4-1b) 式中:N —传递功率(马力,PS )n —转速(r/min )2.扭矩T求出外力偶矩m 后,可进而用截面法求扭转内力——扭矩。
如图4-4所示圆轴,由0=∑x m ,从而可得A —A截面上扭矩TT 称为截面A —A 上的扭矩;扭矩的正负号规定为:按右手螺旋法则,T 矢量离开截面为正,指向截面为负。



薄壁圆筒在弯曲和扭转组合变形下的主应力测试实验
实验目的: (1)了解在弯曲和扭转组合变形情况下的测试方法
(2)测定薄壁圆筒试件在弯曲和扭转组合受力情况下,试件表面某
点的正应力,并与理论值比较。
实验仪器: XL3418材料力学多功能试验台;测力仪;静力电阻应变仪。
实验原理: 薄壁圆筒受弯曲和扭转组合作用,使圆筒的m 点处于平面应力状态如图1所示。
在m 点单元体上有弯矩引起来的正应力x σ,和由扭矩引起来的剪应力n τ。
主应力是一对拉应力1σ和一对压应力3σ。
理论值计算:
132x σσσ= 022n
x
tg τασ-=
x z M W σ= 4
3132z D d W D π⎡⎤
⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ M P L =∆⋅
n T T W τ= 43116T D d W D π⎡⎤
⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦
T P a =∆⋅
实验值计算:
°
°
145453()2(1)E εεσσμ-+=±- °°°°°45-450045-45()2(2)
tg εεαεεε-=
--
图1 圆筒m 点的应力状况。


1薄壁圆筒的弯扭组合变形实验一、试验目的1.测定薄壁圆筒弯扭组合变形时指定点的主应力和主方向,并与理论计算值进行比较。
2.测定薄壁圆筒弯扭组合变形时指定截面上的弯矩、扭矩和剪力引起的应力,并与理论值比较。
3. 学习布片原则、应变成份分析和各种组桥方法。
二、设备和仪器1. 力学试验台。
2. 静态应变仪。
3. 辅助工具和量具。
三、试样与试验装置薄壁圆筒试样(见图5.1a )左端固定,籍固定在圆筒右端的水平杆加载。
圆筒用不锈钢1C r 18N i 9T i 或其它钢材制成,材料弹性模量E 和泊松比µ为己知,或由试验者自行测定,圆筒外径D ,内径d 。
四、试验原理1. 指定点的主应力和主方向测定弯扭组合变形任一截面(如I-I 截面)上b 点的应力状态如图5.1(b)所示,相应其它各测点的应力状态见图 5.1(d)。
根据理论分析可知:弯曲正应力WM M =σ,式中:M=Fl I-I,()143απ−=D W ,D d /=α;薄壁圆筒扭转切应力PT W T=τ,式中:T=Fh ,()16143p απ−=D W ;弯曲切应力Q QF 0 F R tτπ=,()40d D R +=,()2d D t −=;由此可求得相应点的主应力1`2`3σσσ及主方向0α的理论值如何由实验来测定任一截面的主应力和主方向呢?据平面应变分析理论知,若某点任意三个方向的线应变已知,就能计算出该点的主应变和主方向,从而计算出该点的主应力和主方向。
因此测量某点的主应力和主方向时,必须在测点布置三枚应变片,工程中常用应变花 测定。
常见的应变花有45o 应变花和等角应变花等。
在图5.1a 中的I-I 截面的b 、d (或a 、c ),即采用了45o 应变花进行测量,其展示图如图5.61(c)所示。
2采用单臂(多点)半桥公共温度补偿测量法,等量逐级加载。
在每一载荷作用下,分别测得b 、d (或a 、c )两点沿-45o 、0o 、和45o 方向的应变值o o o ``45045εεε−和后,将测量结果记录在实验报告中。

薄壁圆筒扭转试验薄壁圆筒扭转试验如所示纤维复合材料薄壁圆筒纤维与轴线平行,薄壁圆筒平均半径为,壁厚为在簿壁圆筒两端施加对轴线的力偶矩扭矩。
在纤维复合材料薄壁圆筒的扭转试验中假定:当时,可以认为横截面团环上各点切应力沿半径在厚度上均匀分布。
由动员矩守恒原理,对于静力学的纤维复合材料薄壁圆筒问题,各点的切应力满足切应力互等定律。
即:对于内外表面均处于自由状态的纤维复合材料薄壁圆筒,横截面内外因周线上各点切应力均沿团周切线方向铂向。
且由假定可知,同一半径上内外因周线上两点切应力相等。
通过观察可以看出,对于端部受一对外力偶矩,且处在平衡状态的纤维复合材料薄壁圆筒,其外表面上各点处的切应变相同。
该假定给出纤维复合材料薄壁圆筒处于均匀纯剪切应力状态,即对于纤维复合材料薄壁圆筒,由截面法可确定其任意横截面上的扭矩均为。
纤维复合材料湾壁圆筒任意横截面上的扭矩是横截面上分布切应力向轴线简化的主矢量在纤维复合材料荫壁圆筒外表面上任取一点,如图ABC电子所示。
点在弹性主向面内的应力状态如图所示。
对于点弹性主向面内的纯剪切应力状态,当切应力?达到极限应力。
时通过与对应的极限扭矩严可以确定剪切权限应力对于纤维复合材料薄壁圆筒扭转试验,其结果表明,应力—应变之间为非线性关系,如图复合材料单层板沿纤维方向单向拉伸试验确定了复合材料单层板与纤维正交方向单向拉伸试验确定了复合材料单层板与纤维成。
角方向单向拉伸试验确定了纤维复合材料薄壁圆筒纤维与轴线平行的扭转试验确定对于拉伸与压缩强度不相同的复合材料单层扳正交各向异性线弹性体平面应力问题,只须IC现货商将复合材料单层板沿纤维方向单向拉伸试验、复合材料单层板与纤维正交方向单向拉伸试验中的拉仲裁荷换成压缩载荷即可确定。
表给出了种纤维增强复合材料的相关刚度参数及强度指标。
在应用平面应力状态二向最大应力理论的强度条件是应该特别注意,式、式中的应力是正交各向异性线弹性体弹性主向的应力这里下标是弹性主向,并不是应力状态分析中的应力主方向。




材料力学大连理工大学王博
纯剪切
切应力互等定理剪切胡克定律
t r
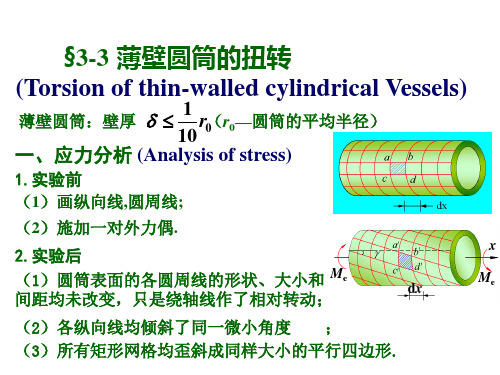
1. 变形特点
圆周线 形状、大小、间距未变
绕轴线旋转不同角度
纵向线 间距未变,倾斜角度相同
一、横截面上的切应力(目的:由内力表征出应力)
薄壁圆筒扭转 纯剪切
什么是薄壁圆筒? ——壁厚 t 远小于平均半径 r
圆周线 纵向线
2. 横截面上的应力
猜测(特点)切应力τ
σ = 0 ;
(2)大小 沿壁厚均匀分布、
数值由静力学关系求得
(1)方向 垂直于所在半径、 对轴线的矩与扭矩一致
Q :从合力的作用效果分析,切应力与之前所学的连接件切应力有何不同? F τ τ
τ ≠ 0 推断(有无) M e T
得 t T
r
或 其中A 0为壁厚中线所围的面积
由静力等效 ⎰=⋅⋅=⋅A
T
r t r A r τπτ2d 22πT r t τ=02T A t τ=t
T r 2
0πA r =d A τd A
x y
z 二、切应力互等定理
Theorem of Conjugate Shearing Stress 应力单元体特点 1.各边长无穷小 2.各面应力均匀分布 3.平行两面对应应力数值相等 d y d x d z y z x d x
d y d z
τ'
∑M x =0, ∴ 定理 在互相垂直的两个截面上
1.垂直于截面交线的切应力数值相等
2.方向同时指向截面交线,
或同时背离截面交线 τ()()d d d d d d 0x y z x z y ττ'-==ττ'
圆筒扭转横截面边缘各点切应力τ的方向
为什么一定与边线相切(垂直于半径)?
切应力互等定理——小试牛刀!!
τM e
τ
τ
τ
T
τ τ
三、剪切胡克定律 Hooke ’s Law in Shear τ
τ γ γ 回忆 材料的拉压胡克定律 当 σ ε
σp P =E σσσε≤,
弹性常数之关系 当 τ ≤ τp
τ = Gγ
式中 τp — 剪切比例极限
G — 切变模量 Shear Modulus 单位 GPa τ © 变形后 线性
剪切胡克定律 τ τ γ τp ()ν+=12E G。