薄壁圆筒的扭转

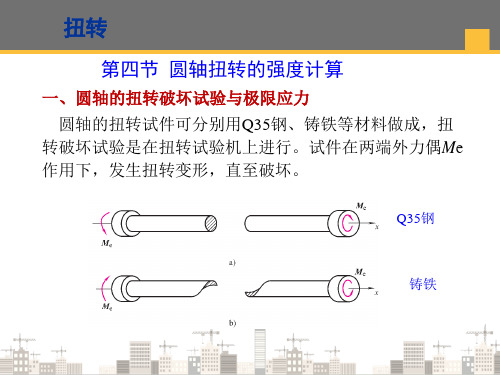
材料力学大连理工大学王博纯剪切切应力互等定理剪切胡克定律t r1. 变形特点圆周线 形状、大小、间距未变绕轴线旋转不同角度纵向线 间距未变，倾斜角度相同一、横截面上的切应力（目的：由内力表征出应力）薄壁圆筒扭转 纯剪切什么是薄壁圆筒? ——壁厚 t 远小于平均半径 r圆周线 纵向线2. 横截面上的应力猜测（特点）切应力τσ = 0 ；（2）大小 沿壁厚均匀分布、数值由静力学关系求得（1）方向 垂直于所在半径、 对轴线的矩与扭矩一致Q ：从合力的作用效果分析，切应力与之前所学的连接件切应力有何不同？ F τ ττ ≠ 0 推断（有无） M e T得 t Tr或 其中A 0为壁厚中线所围的面积由静力等效 ⎰=⋅⋅=⋅ATr t r A r τπτ2d 22πT r t τ=02T A t τ=tT r 20πA r =d A τd Ax yz 二、切应力互等定理Theorem of Conjugate Shearing Stress 应力单元体特点 1.各边长无穷小 2.各面应力均匀分布 3.平行两面对应应力数值相等 d y d x d z y z x d xd y d zτ'∑M x =0， ∴ 定理 在互相垂直的两个截面上1.垂直于截面交线的切应力数值相等2.方向同时指向截面交线，或同时背离截面交线 τ()()d d d d d d 0x y z x z y ττ'-==ττ'圆筒扭转横截面边缘各点切应力τ的方向为什么一定与边线相切（垂直于半径）？切应力互等定理——小试牛刀！！τM eτττTτ τ三、剪切胡克定律 Hooke ’s Law in Shear ττ γ γ 回忆 材料的拉压胡克定律 当 σ εσp P =E σσσε≤，弹性常数之关系 当 τ ≤ τpτ = Gγ式中 τp — 剪切比例极限G — 切变模量 Shear Modulus 单位 GPa τ © 变形后 线性剪切胡克定律 τ τ γ τp ()ν+=12E G。

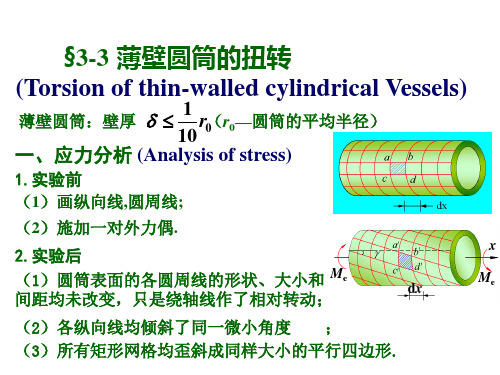
薄壁圆筒扭转试验薄壁圆筒扭转试验如所示纤维复合材料薄壁圆筒纤维与轴线平行，薄壁圆筒平均半径为，壁厚为在簿壁圆筒两端施加对轴线的力偶矩扭矩。

在纤维复合材料薄壁圆筒的扭转试验中假定：当时，可以认为横截面团环上各点切应力沿半径在厚度上均匀分布。

由动员矩守恒原理，对于静力学的纤维复合材料薄壁圆筒问题，各点的切应力满足切应力互等定律。

即：对于内外表面均处于自由状态的纤维复合材料薄壁圆筒，横截面内外因周线上各点切应力均沿团周切线方向铂向。

且由假定可知，同一半径上内外因周线上两点切应力相等。

通过观察可以看出，对于端部受一对外力偶矩，且处在平衡状态的纤维复合材料薄壁圆筒，其外表面上各点处的切应变相同。

该假定给出纤维复合材料薄壁圆筒处于均匀纯剪切应力状态，即对于纤维复合材料薄壁圆筒，由截面法可确定其任意横截面上的扭矩均为。

纤维复合材料湾壁圆筒任意横截面上的扭矩是横截面上分布切应力向轴线简化的主矢量在纤维复合材料荫壁圆筒外表面上任取一点，如图ABC电子所示。

点在弹性主向面内的应力状态如图所示。

对于点弹性主向面内的纯剪切应力状态，当切应力?达到极限应力。

时通过与对应的极限扭矩严可以确定剪切权限应力对于纤维复合材料薄壁圆筒扭转试验，其结果表明，应力—应变之间为非线性关系，如图复合材料单层板沿纤维方向单向拉伸试验确定了复合材料单层板与纤维正交方向单向拉伸试验确定了复合材料单层板与纤维成。

角方向单向拉伸试验确定了纤维复合材料薄壁圆筒纤维与轴线平行的扭转试验确定对于拉伸与压缩强度不相同的复合材料单层扳正交各向异性线弹性体平面应力问题，只须IC现货商将复合材料单层板沿纤维方向单向拉伸试验、复合材料单层板与纤维正交方向单向拉伸试验中的拉仲裁荷换成压缩载荷即可确定。

表给出了种纤维增强复合材料的相关刚度参数及强度指标。

在应用平面应力状态二向最大应力理论的强度条件是应该特别注意，式、式中的应力是正交各向异性线弹性体弹性主向的应力这里下标是弹性主向，并不是应力状态分析中的应力主方向。

薄圆筒的转动惯量
转动惯量是刚体绕轴转动时惯性大小的量度，通常用J表示，其单位为kg·m²。

对于薄圆筒，其转动惯量可以通过以下公式计算：
J=MR²
其中，M表示圆筒的质量，R表示圆筒的外半径。

在实际应用中，圆筒的壁厚通常较薄，可以忽略不计，因此可以将其视为空心薄壁圆筒。

该公式适用于各种形状和尺寸的薄圆筒，为相关的工程和设计提供了便利。

如果需要计算更复杂形状的转动惯量，可以将其分解为多个简单的部分，分别计算各部分的转动惯量，然后相加得到总的转动惯量。

薄壁圆筒扭转功率mw2r2薄壁圆筒扭转功率MW2R2的研究引言薄壁圆筒扭转功率（MW2R2）是用来描述材料在受到扭转作用时所产生的能量转换效率的指标。

薄壁圆筒扭转功率的研究对于加深人们对材料力学性能的理解，并为工程设计提供可靠依据具有重要意义。

本文将深入探讨薄壁圆筒扭转功率的相关理论与实践，以期为该领域的研究提供一定的参考。

一、薄壁圆筒扭转功率的定义与计算方法薄壁圆筒扭转功率指的是材料在扭转过程中所消耗的能量与施加的扭转作用所做的功之间的比值。

它可以用数学公式MW2R2来表示，其中M为扭转力矩，W为角位移，R为圆筒半径。

按照力学原理，扭转功率可以表示为MW2R2=Tω，其中T为扭转力，ω为角速度。

根据上述计算方法，我们可以得出薄壁圆筒扭转功率的数值，从而进一步分析材料在扭转过程中的性能表现。

二、薄壁圆筒扭转功率的实验研究为了验证薄壁圆筒扭转功率的计算方法，并进一步了解其在实际应用中的表现，人们进行了一系列的实验研究。

首先，研究人员选取了不同材质和尺寸的薄壁圆筒进行了扭转实验。

他们测量了扭转力矩、角速度和圆筒半径等参数，并计算出了相应的扭转功率。

通过对不同材料和尺寸的圆筒进行对比分析，研究人员得出了许多有价值的结论。

其次，研究人员还通过改变薄壁圆筒的几何形状和内外部环境，进一步研究了薄壁圆筒扭转功率的变化规律。

他们发现，不同的几何形状和不同的环境因素对薄壁圆筒的扭转功率有着显著的影响。

这些实验结果为薄壁圆筒的设计和使用提供了重要的理论依据。

三、薄壁圆筒扭转功率的应用与展望薄壁圆筒扭转功率在工程设计中具有广泛的应用价值。

首先，它可以用来评估材料的扭转性能。

在材料选择和制造工艺优化中，薄壁圆筒扭转功率可以帮助工程师更好地理解材料的力学特性，从而选择合适的材料和工艺。

其次，薄壁圆筒扭转功率也可以用来评估工程结构的稳定性。

通过对结构扭转过程中能量转换效率的研究，我们可以得出结构的稳定性指标，从而判断结构在扭转荷载下的安全性。