第三章 -材料力学扭转
- 格式:ppt
- 大小:2.55 MB
- 文档页数:56

《钢铁是怎样炼成》第三章主要内容
《钢铁是怎样炼成》第三章内容主要介绍了钢铁的淬火、拔丝和
粗精调节过程,描述了生产钢铁的具体工艺步骤。
淬火是将钢水烧到其最佳硬度将其浸渍在含有各种化合物的熔融
液中的一种工艺手段。
它是一个比较重要的工艺,是钢铁行业热处理
的最重要部分。
淬火能改变和改善钢铁材料的性能,提高强度和硬度,降低可塑性,改善钢的焊接性能。
拔丝是一种表面精铣加工技术,它通常是用来制作构造单元和上
部件的表面精度。
它通过安装在机床上的精度密封锯片,切削钢板平整,它的平整度是不可接受的,有时它甚至会产生裂纹,所以在拔丝
之前必须要进行粗磨和粗加工。
粗精调节是指对已经拔丝处理后的钢板,采用粗砂轮对其进行精
加工,使表面质量达到较高的要求。
为了使表面质量符合要求,必须
使用精度较高的磨具,精心选取砂轮,并仔细调整装置,以保证表面
粗糙度符合要求。



高考数学第三章知识点总结第一节直线和方程1. 直线的方程直线的方程有两种常见的表示方法:一般式和斜截式。
一般式是Ax+By+C=0,斜截式是y=kx+b。
2. 直线的性质直线有斜率和倾斜角的概念,斜率是直线的倾斜程度,倾斜角是与x轴的夹角。
3. 直线与坐标轴的交点直线与x轴的交点是y=0处的x坐标,与y轴的交点是x=0处的y坐标。
第二节函数及其性质1. 函数的概念函数是自变量和因变量之间的对应关系,表示为y=f(x)。
2. 函数的性质函数有定义域、值域、单调性、奇偶性等性质。
3. 基本初等函数的性质基本初等函数包括常函数、一次函数、二次函数、指数函数、对数函数、幂函数和三角函数等。
4. 函数的图像和性质函数的图像可以通过函数的定义域、值域、单调性、极值、奇偶性等来描述。
第三节数列和级数1. 数列的概念数列是按照一定规律排列的数字序列,可以是等差数列、等比数列、斐波那契数列等。
2. 数列的通项公式数列的通项公式可以用来表示数列的任意一项的通用表达式。
3. 级数的概念级数是数列的和的概念,可以是等差级数、等比级数等。
4. 级数的性质级数有收敛和发散的性质,可以通过极限的概念来分析级数的和是否存在。
第四节不等式与不等式组1. 不等式的性质不等式有加法、减法、乘法、除法以及取对数、指数等运算的性质。
2. 一元一次不等式一元一次不等式可以用图像法或者代数法来解决。
3. 一元二次不等式一元二次不等式可以通过解二次方程的方法来求解。
4. 不等式组不等式组是由多个不等式组成的方程组,可以用图像法、代数法来解决。
结尾总结高考数学第三章主要涉及直线和方程、函数及其性质、数列和级数、不等式与不等式组等知识点。
这些知识点在解决各种数学问题时起着至关重要的作用,掌握这些知识对于高考数学的学习至关重要。
希望同学们能够通过系统的学习和练习,掌握这些知识,为高考取得优异成绩打下坚实的基础。



钢铁是怎样炼成的第三章主要内容
钢铁是怎样炼成的第三章主要内容:
保尔在湖边钓鱼时,结识了林务官的女儿冬妮娅。
她没有像别的富家子女一样明弄和侮辱保尔,两人很快认识了。
车站的工人们罢了工,阿尔焦姆等三位工人在被迫开车时,为了自己和其他起义年的安全系了一个德国人,之后跳车逃到乡下。
但他们的家人打听不到他们的消息.了。
冬妮娅在湖边读书,看见了游泳的保尔。
他们在一起聊天,成了朋友。
保尔为了养活自己和妈妈,再买一套新衣服,又找了一份锯木的工作。
打扮一新的保尔让冬妮娅很惊喜。
本书主要内容:
这本书讲述了主人公保尔·柯察金从一个在社会底层挣扎的贫苦少年,逐渐成长为一个为祖国和人民的事业奋斗毕生的无产阶级革命战士的历程。
年少的保尔曾做过店员,任人欺侮;偷过德国人的手枪,因救朱赫来而坐牢;辗转于硝烟弥漫的战场,多次挣扎在死亡线上。
革命胜利之后他又将全部身心投入了国民建设当中。
在这个过程中,保尔表现出了一个真正的无产阶级革命战士所具有的坚毅、勇敢、无私奉献的高尚品格,他把自己宝贵的青春交给了党和人民,在全身瘫痪的情况下仍勇敢地拿起笔服务于人民。
保尔的精神是一面永恒的旗帜,保尔的事迹和品格是每一个21世纪青少年学习的榜样。
电源和电流【引入】前面的两章我们都在学习静电场,激发静电场的是静止电荷。
那么电荷运动起来又会有什么作用呢?其实早在初中我们就学习了,电荷的定向移动产生了电流。
这一节课我们进一步思考,电荷在怎样的条件下会定向移动。
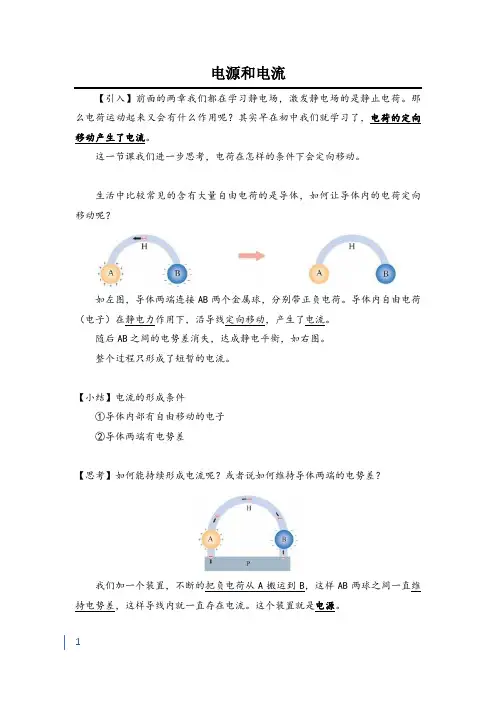
生活中比较常见的含有大量自由电荷的是导体,如何让导体内的电荷定向移动呢?如左图,导体两端连接AB两个金属球,分别带正负电荷。
导体内自由电荷(电子)在静电力作用下,沿导线定向移动,产生了电流。
随后AB之间的电势差消失,达成静电平衡,如右图。
整个过程只形成了短暂的电流。
【小结】电流的形成条件①导体内部有自由移动的电子②导体两端有电势差【思考】如何能持续形成电流呢?或者说如何维持导体两端的电势差?我们加一个装置,不断的把负电荷从A搬运到B,这样AB两球之间一直维持电势差,这样导线内就一直存在电流。
这个装置就是电源。
一、电源1.定义表述1:把电子持续的从正极搬运到负极的装置。
这个过程中在克服静电力做功,把其它能量转化为电能。
表述2:通过非静电力做功,把其它形式的能量转化为电能。
2.作用维持正负极之间的电势差,来维持电流。
在电源两极电荷、导线电荷的作用下,空间中形成了大小、方向都十分稳定的电场——恒定电场。
二、恒定电场1.定义由稳定分布的电荷激发的电场,强弱、方向都不变化。
注:(1)虽然电荷在定向移动,但是总会得到等量的补充,形成了动态稳定。
(2)恒定电场不是静电场。
但是在静电场中的电学概念同样适用。
2.导线中的恒定电场导线中的恒定电场是沿着导线方向的。
这个电场是接通电源后以光速建立的。
导线中的电荷在恒定电场的作用下形成了恒定电流。
三、恒定电流(一)概念大小和方向都不随时间变化的电流产生条件:①自由电荷②稳定的电场注:金属中自由电荷是电子;溶液中自由电荷是阴阳离子(二)电流大小单位时间内通过导线横截面的电荷量1.决定式I=qt单位:安培(A)电子定向移动速率为v、导线横截面积为s、单位体积内有电子n则,通过电荷量=通过体积*n*eq=svtne2.微观表达式I=neSv注:这里的e是电子的带电量(三)电流方向规定正电荷定向移动的方向为电流方向。

第三章 缓冲溶液习题参考答案1. 在1L 1.0×10-5mol ·L -1 NaOH 溶液中,加入0.001molNaOH 或HCl ,溶液的pH 怎样改变?解:ΔpH 1≈11-9=2;ΔpH 2≈3-9=-62. 设有下列三种由乳酸和乳酸钠组成的缓冲溶液,分别计算它们的pH 值(25℃时乳酸的K a = 1.4×10-4)。
(1)1L 溶液中含有0.1mol 乳酸和0.1mol 乳酸钠。
(2)1L 溶液中含0.1mol 乳酸和0.01mol 乳酸钠。
(3)1L 溶液中含0.01mol 乳酸和0.1mol 乳酸钠。
解:(1)85.31.01.0lg )104.1lg(lg p [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n K K (2)85.21.001.0lg )104.1lg(lg [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n pK K (3)85.401.01.0lg )104.1lg(lg [HB]][B lg p pH 4HB B a a =+⨯-=+=+=--n n pK K 3. 正常血浆中具有H 2PO 4--HPO 42-缓冲系,H 2PO 4-的p K a2 = 6.8(校正后),已知正常血浆中[HPO 42-]/[H 2PO 4-]为4/1,试求血浆的pH 值;尿中[HPO 42-]/[H 2PO 4-]为1/9,试求尿的pH 值。
解:血浆的pH 值:40.714lg 8.6[HB]][B lg p pH a =+=+=-K 尿液的pH 值:84.591lg 8.6[HB]][B lg p pH a =+=+=-K 4. 将0.15mol ·L -1 NaOH 溶液0.1mL 加于10mL pH 值为4.74的缓冲溶液中,溶液的pH 值变为4.79,试求此缓冲溶液的缓冲容量。

西⽠书课后习题——第三章3.1式3.2 f(x)=ωT x+b中,ωT和b有各⾃的意义,简单来说,ωT决定学习得到模型(直线、平⾯)的⽅向,⽽b则决定截距,当学习得到的模型恰好经过原点时,可以不考虑偏置项b。
偏置项b实质上就是体现拟合模型整体上的浮动,可以看做是其它变量留下的偏差的线性修正,因此⼀般情况下是需要考虑偏置项的。
但如果对数据集进⾏了归⼀化处理,即对⽬标变量减去均值向量,此时就不需要考虑偏置项了。
3.2对区间[a,b]上定义的函数f(x),若它对区间中任意两点x1,x2均有f(x1+x22)≤f(x1)+f(x2)2,则称f(x)为区间[a,b]上的凸函数。
对于实数集上的函数,可通过⼆阶导数来判断:若⼆阶导数在区间上⾮负,则称为凸函数,在区间上恒⼤于零,则称为严格凸函数。
对于式3.18 y=11+e−(ωT x+b),有dydωT=1(1+e−(ωT x+b))2e−(ωT x+b)(−x)=(−x)11+e−(ωT x+b)(1−11+e−(ωT x+b))=xy(y−1)=x(y2−y)d dωT(dydωT)=x(2y−1)(dydωT)=x2y(2y−1)(y−1)其中,y的取值范围是(0,1),不难看出⼆阶导有正有负,所以该函数⾮凸。
3.3对率回归即Logis regression西⽠集数据如图所⽰:将好⽠这⼀列变量⽤0/1变量代替,进⾏对率回归学习,python代码如下:import numpy as npimport matplotlib.pyplot as pltimport pandas as pdfrom sklearn import model_selectionfrom sklearn.linear_model import LogisticRegressionfrom sklearn import metricsdataset = pd.read_csv('/home/zwt/Desktop/watermelon3a.csv')#数据预处理X = dataset[['密度','含糖率']]Y = dataset['好⽠']good_melon = dataset[dataset['好⽠'] == 1]bad_melon = dataset[dataset['好⽠'] == 0]#画图f1 = plt.figure(1)plt.title('watermelon_3a')plt.xlabel('density')plt.ylabel('radio_sugar')plt.xlim(0,1)plt.ylim(0,1)plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='o',color='r',s=100,label='bad')plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='o',color='g',s=100,label='good')plt.legend(loc='upper right')#分割训练集和验证集X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0) #训练log_model = LogisticRegression()log_model.fit(X_train,Y_train)#验证Y_pred = log_model.predict(X_test)#汇总print(metrics.confusion_matrix(Y_test, Y_pred))print(metrics.classification_report(Y_test, Y_pred, target_names=['Bad','Good']))print(log_model.coef_)theta1, theta2 = log_model.coef_[0][0], log_model.coef_[0][1]X_pred = np.linspace(0,1,100)line_pred = theta1 + theta2 * X_predplt.plot(X_pred, line_pred)plt.show()View Codeimport numpy as npimport matplotlib.pyplot as pltimport pandas as pdfrom sklearn import model_selectionfrom sklearn.linear_model import LogisticRegressionfrom sklearn import metricsdataset = pd.read_csv('/home/zwt/Desktop/watermelon3a.csv')#数据预处理X = dataset[['密度','含糖率']]Y = dataset['好⽠']good_melon = dataset[dataset['好⽠'] == 1]bad_melon = dataset[dataset['好⽠'] == 0]#画图f1 = plt.figure(1)plt.title('watermelon_3a')plt.xlabel('density')plt.ylabel('radio_sugar')plt.xlim(0,1)plt.ylim(0,1)plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='o',color='r',s=100,label='bad')plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='o',color='g',s=100,label='good')plt.legend(loc='upper right')#分割训练集和验证集X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0) #训练log_model = LogisticRegression()log_model.fit(X_train,Y_train)#验证Y_pred = log_model.predict(X_test)#汇总print(metrics.confusion_matrix(Y_test, Y_pred))print(metrics.classification_report(Y_test, Y_pred))print(log_model.coef_)theta1, theta2 = log_model.coef_[0][0], log_model.coef_[0][1]X_pred = np.linspace(0,1,100)line_pred = theta1 + theta2 * X_predplt.plot(X_pred, line_pred)plt.show()View Code模型效果输出(查准率、查全率、预测效果评分):precision recall f1-score supportBad 0.75 0.60 0.67 5Good 0.60 0.75 0.67 4micro avg 0.67 0.67 0.67 9macro avg 0.68 0.68 0.67 9weighted avg 0.68 0.67 0.67 9也可以输出验证集的实际结果和预测结果:密度含糖率 Y_test Y_pred1 0.774 0.376 1 16 0.481 0.149 1 08 0.666 0.091 0 09 0.243 0.267 0 113 0.657 0.198 0 04 0.556 0.215 1 12 0.634 0.264 1 114 0.360 0.370 0 110 0.245 0.057 0 03.4⾸先附上使⽤葡萄酒品质数据做的对率回归学习代码import numpy as npimport matplotlib.pyplot as pltimport pandas as pdpd.set_option('display.max_rows',None)pd.set_option('max_colwidth',200)pd.set_option('expand_frame_repr', False)from sklearn import model_selectionfrom sklearn.linear_model import LogisticRegressionfrom sklearn import metricsdataset = pd.read_csv('/home/zwt/Desktop/winequality-red_new.csv')#数据预处理dataset['quality2'] = dataset['quality'].apply(lambda x: 0 if x < 5 else 1) #新加⼊⼆分类变量是否为好酒,基于原数据中quality的值,其⼤于等于5就定义为好酒,反之坏酒X = dataset[["fixed_acidity","volatile_acidity","citric_acid","residual_sugar","chlorides","free_sulfur_dioxide","total_sulfur_dioxide","density","pH","sulphates","alcohol"]]Y = dataset["quality2"]#分割训练集和验证集X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0)#训练log_model = LogisticRegression()log_model.fit(X_train,Y_train)#验证Y_pred = log_model.predict(X_test)#汇总print(metrics.confusion_matrix(Y_test, Y_pred))print(metrics.classification_report(Y_test, Y_pred))print(log_model.coef_)View Code其中,从UCI下载的数据集格式有问题,⽆法直接使⽤,先编写程序将格式调整完毕再使⽤数据fr = open('/home/zwt/Desktop/winequality-red.csv','r',encoding='utf-8')fw = open('/home/zwt/Desktop/winequality-red_new.csv','w',encoding='utf-8')f = fr.readlines()for line in f:line = line.replace(';',',')fw.write(line)fr.close()fw.close()View Code两种⽅法的错误率⽐较from sklearn.linear_model import LogisticRegressionfrom sklearn import model_selectionfrom sklearn.datasets import load_wine# 载⼊wine数据dataset = load_wine()#10次10折交叉验证法⽣成训练集和测试集def tenfolds():k = 0truth = 0while k < 10:kf = model_selection.KFold(n_splits=10, random_state=None, shuffle=True)for x_train_index, x_test_index in kf.split(dataset.data):x_train = dataset.data[x_train_index]y_train = dataset.target[x_train_index]x_test = dataset.data[x_test_index]y_test = dataset.target[x_test_index]# ⽤对率回归进⾏训练,拟合数据log_model = LogisticRegression()log_model.fit(x_train, y_train)# ⽤训练好的模型预测y_pred = log_model.predict(x_test)for i in range(len(x_test)): #这⾥和留⼀法不同,是因为10折交叉验证的验证集是len(dataset.target)/10,验证集的预测集也是,都是⼀个列表,是⼀串数字,⽽留⼀法是⼀个数字if y_pred[i] == y_test[i]:truth += 1k += 1# 计算精度accuracy = truth/(len(x_train)+len(x_test)) #accuracy = truth/len(dataset.target)print("⽤10次10折交叉验证对率回归的精度是:", accuracy)tenfolds()#留⼀法def leaveone():loo = model_selection.LeaveOneOut()i = 0true = 0while i < len(dataset.target):for x_train_index, x_test_index in loo.split(dataset.data):x_train = dataset.data[x_train_index]y_train = dataset.target[x_train_index]x_test = dataset.data[x_test_index]y_test = dataset.target[x_test_index]# ⽤对率回归进⾏训练,拟合数据log_model = LogisticRegression()log_model.fit(x_train, y_train)# ⽤训练好的模型预测y_pred = log_model.predict(x_test)if y_pred == y_test:true += 1i += 1# 计算精度accuracy = true / len(dataset.target)print("⽤留⼀法验证对率回归的精度是:", accuracy)leaveone()View Code3.5import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.discriminant_analysis import LinearDiscriminantAnalysisfrom sklearn import model_selectionfrom sklearn import metricsdataset = pd.read_csv('/home/zwt/Desktop/watermelon3a.csv')#数据预处理X = dataset[['密度','含糖率']]Y = dataset['好⽠']#分割训练集和验证集X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.5,random_state=0)#训练LDA_model = LinearDiscriminantAnalysis()LDA_model.fit(X_train,Y_train)#验证Y_pred = LDA_model.predict(X_test)#汇总print(metrics.confusion_matrix(Y_test, Y_pred))print(metrics.classification_report(Y_test, Y_pred, target_names=['Bad','Good']))print(LDA_model.coef_)#画图good_melon = dataset[dataset['好⽠'] == 1]bad_melon = dataset[dataset['好⽠'] == 0]plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='o',color='r',s=100,label='bad')plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='o',color='g',s=100,label='good')View Codeimport numpy as npimport matplotlib.pyplot as pltdata = [[0.697, 0.460, 1],[0.774, 0.376, 1],[0.634, 0.264, 1],[0.608, 0.318, 1],[0.556, 0.215, 1],[0.403, 0.237, 1],[0.481, 0.149, 1],[0.437, 0.211, 1],[0.666, 0.091, 0],[0.243, 0.267, 0],[0.245, 0.057, 0],[0.343, 0.099, 0],[0.639, 0.161, 0],[0.657, 0.198, 0],[0.360, 0.370, 0],[0.593, 0.042, 0],[0.719, 0.103, 0]]#数据集按⽠好坏分类data = np.array([i[:-1] for i in data])X0 = np.array(data[:8])X1 = np.array(data[8:])#求正反例均值miu0 = np.mean(X0, axis=0).reshape((-1, 1))miu1 = np.mean(X1, axis=0).reshape((-1, 1))#求协⽅差cov0 = np.cov(X0, rowvar=False)cov1 = np.cov(X1, rowvar=False)#求出wS_w = np.mat(cov0 + cov1)Omiga = S_w.I * (miu0 - miu1)#画出点、直线plt.scatter(X0[:, 0], X0[:, 1], c='b', label='+', marker = '+')plt.scatter(X1[:, 0], X1[:, 1], c='r', label='-', marker = '_')plt.plot([0, 1], [0, -Omiga[0] / Omiga[1]], label='y')plt.xlabel('密度', fontproperties='SimHei', fontsize=15, color='green');plt.ylabel('含糖率', fontproperties='SimHei', fontsize=15, color='green');plt.title(r'LinearDiscriminantAnalysis', fontproperties='SimHei', fontsize=25);plt.legend()plt.show()View Code3.6对于⾮线性可分的数据,要想使⽤判别分析,⼀般思想是将其映射到更⾼维的空间上,使它在⾼维空间上线性可分进⼀步使⽤判别分析。
《童年》的第三章主要内容(大全)一、【课文《童年》的第三章主要内容】第三章主要写了:两个舅舅捉弄格里高利;外祖母给“我”讲小茨冈的身世;小茨冈玩的游戏,在家庭舞会上跳舞;格里高利给“我”讲舅舅雅可夫折磨死舅妈的事。
小茨冈外出购物,外祖母担心他,他回来时,外祖父盘问花了多少钱,舅舅们盘问留了多少回扣,外祖母担心小茨冈偷东西会被报复。
两个舅舅让小茨冈背一个两人都抬不动的十字架,小茨冈背十字架压死。
二、【课文《童年》的重要部分的阅读批注】1.“两个舅舅总是捉弄格里高利,他只是默默忍受。
”两个舅舅把快乐建立在他人的痛苦之上。
舅舅恶作剧捉弄格里高利,为的是将来想让格里高利为自己干活。
可是舅舅真的很残忍。
小茨冈玩蟑螂、老鼠、扑克牌等游戏,在残忍、苦难的家庭里寻求慰籍,他热爱生活。
家庭晚会上,每个人都开心,特别是小茨冈,俄罗斯人民虽然生活在苦难、残酷的时代,但是也有乐观心态。
“晚会上,雅可夫,萨沙听吉他乐,雅可夫弹奏的细节动作表现出他的快乐和沉醉。
萨沙倾听时的细节动作表现出如醉如痴的状态。
”2.小茨冈舞步的优美该如何表现?作者使用比喻,把跳舞的小茨冈比成老鹰翱翔、雨燕盘旋、火焰燃烧,形象而有画面感。
3.“外祖父派小茨冈外出买东西,就是图他诚实、省钱,能偷,外祖父用最少的钱得到最多的东西。
外祖父连两个儿子都不放心。
”谁都想从小茨冈身上捞一把,两个舅舅经常盘剥小茨冈,小茨冈只好偷东西,这样才能获得别人单位认可。
他很天真,也很愚蠢。
外祖父吝啬、不信任儿子,所以让小茨买东西,两个舅舅认为小茨冈是“肥肉”。
所有人都是那么贪婪,就和狼一样,只有外祖母关心小茨冈的安危,怕他偷东西被抓住挨打。
两个舅舅除了盘剥小茨冈,要欺凌他,让他背数倍重的十字架,这是在折磨,他们用残暴的方式来获得快感。
小茨冈因为自己的愚蠢,被压在了十字架下面,讨别人欢心,反而被害死。
小茨冈被压重伤了,没有人为他伸张,只有格里高利表达了不满。
4.小茨冈临死前的惨状怎么写?作者高超地抓住了:全身发黑(整体写),头发黑得发青,手指不动。
第三章小测及答案2010.10.20一、填空(注:带“※”的对专科不作要求)1.卡诺循环是由以下四个可逆步骤构成的:恒温可逆膨胀、绝热可逆膨胀、恒温可逆压缩、绝热可逆压缩,是一种理想化的循环,它的一个重要性质是Q1/T1 +Q2/T2 =0。
2.卡诺热机的效率只与高低温两热源的温度有关,与工质及变化的种类无关。
3.应用吉布斯函数判据的条件是:dT=0、dP=0、W′=0、封闭系统。
4.克拉佩龙方程应用于纯物质的任意两相平衡,克劳修斯-克拉佩龙方程应用于纯物质的气-液平衡或气-固平衡。
5.熵的物理意义的定性解释是:熵是量度系统无序度的函数。
6.热力学第三定律是以修正后的普朗克说法为基准,内容是0K时纯物质完美晶体的熵值为零,原始形式是能斯特热定理。
7.自发过程具有方向性,一定是不可逆过程,它的进行造成系统作功能力的损失。
绝热不可逆过程8.熵增原理的数学表达式是△S≧0 绝热可逆过程。
9.逆向的卡诺循环是热泵、冷冻机的工作原理。
10.热力学第二定律是用来判断过程可能性及限度的定律,第三定律是用来确定化学反应熵值计算的基准。
不可逆过程11.克劳修斯不等式:dS≧δQ/T 可逆过程。
12.热力学第二定律的克劳修斯说法是:热不可能自动地从低温流向高温。
13.应用亥姆霍兹函数判据的条件是:dT=0 、dV=0 、W′=0 、封闭系统。
14.目前可用来判断过程可能性的判据有:熵判据、吉布斯函数判据、亥姆霍兹函数判据。
※15.节流膨胀过程是恒焓过程。
※16.对于理想气体,焦耳-汤姆孙系数μJ-T = 0。
※17.使气体致冷的节流膨胀,其焦耳-汤姆逊系数μ必须大于零。
J,T18. 公式 ∆G = ∆H - T ∆S 的适用条件是 恒温 , 封闭系统 。
19. 某可逆热机分别从600 K 和1000 K 的高温热源吸热,向300 K 的冷却水放热。
问每吸收100 kJ 的热量,对环境所作的功-W r 分别为: -50KJ 和-70KJ 。