概率论与数理统计-浙江大学数学系.

格式：ppt
大小：806.00 KB
文档页数：30

下载文档原格式

概率论与数理统计-浙江大学数学系

8
定理5.2 契比雪夫定理的特殊情形：设随机变量序列X 1 , X 2 , , X n , 相互独立，且具有相同的数学期望和相同的方差 2，作前n个随机变量的算术平均： Yn 1 X k , n k 1
n
则 0，有：
1 n lim P Yn lim P X k 1. n n n k 1 n 1 P 即， X k . n k 1 1 n 证明：由于E Yn E X k 1 n , n k 1 n 2 1 n 1 n 2 1 D Yn D X k 2 D X k 2 n n n n k 1 n k 1
师介绍——》统计研究所——》张彩伢
►
2
第五章大数定律和中心极限定理
关键词：契比雪夫不等式
大数定律中心极限定理
3
§1 大数定律
背景
本章的大数定律，对第一章中提出的 “频率稳定性”，给出理论上的论证
为了证明大数定理，先介绍一个重要不等式
4
定理5.1 契比雪夫不等式：设随机变量X 具有数学期望E X , 方差D X 2
此外，定理中要求随机变量的方差存在，但当随机变量服从相同分布时，就不需要这一要求。
定理5.3 辛钦定理：设随机变量序列X 1 , X 2 , , X n , 相互独立，服从同一分布，且存在数学期望，作前n个随机变量的算术平均：Yn 1 X k n k 1 则 0，有： 1 n lim P Yn lim P X k 1. n n n k 1
§2 中心极限定理
背景：
有许多随机变量，它们是由大量的相互独立的随机变量的综合影响所形成的，而其中每个个别的因素作用都很小，这种随机变量往往服从或近似服从正态分布，或者说它的极限分布是正态分布，中心极限定理正是从数学上论证了这一现象，它在长达两个世纪的时期内曾是概率论研究的中心课题。

概率论与数理统计课后习题答案浙江大学第四版完整版.pdf

完全版概率论与数理统计课后习题答案第四版盛骤(浙江大学)浙大第四版（高等教育出版社）第一章概率论的基本概念1.[一]写出下列随机试验的样本空间（1）记录一个小班一次数学考试的平均分数（充以百分制记分）（[一]1）nn n n o S1001, ，n 表小班人数（3）生产产品直到得到10件正品，记录生产产品的总件数。

（[一]2）S={10，11，12，………，n ，………}（4）对某工厂出厂的产品进行检查，合格的盖上“正品”，不合格的盖上“次品”，如连续查出二个次品就停止检查，或检查4个产品就停止检查，记录检查的结果。

查出合格品记为“1”，查出次品记为“0”，连续出现两个“0”就停止检查，或查满4次才停止检查。

（[一](3)）S={00，100，0100，0101，1010，0110，1100，0111，1011，1101，1110，1111，}2.[二]设A ，B ，C 为三事件，用A ，B ，C 的运算关系表示下列事件。

（1）A 发生，B 与C 不发生。

表示为：C B A 或A －(AB+AC )或A －(B ∪C )（2）A ，B 都发生，而C 不发生。

表示为：C AB 或AB －ABC 或AB －C（3）A ，B ，C 中至少有一个发生表示为：A+B+C（4）A ，B ，C 都发生，表示为：ABC（5）A ，B ，C 都不发生，表示为：C B A 或S －(A+B+C)或CB A（6）A ，B ，C 中不多于一个发生，即A ，B ，C 中至少有两个同时不发生相当于C A C B B A ,,中至少有一个发生。

故表示为：C A C B B A 。

（7）A ，B ，C 中不多于二个发生。

相当于：C B A ,,中至少有一个发生。

故表示为：ABCC B A 或（8）A ，B ，C 中至少有二个发生。

相当于：AB ，BC ，AC 中至少有一个发生。

故表示为：AB +BC +AC6.[三]设A ，B 是两事件且P (A )=0.6，P (B )=0.7.问(1)在什么条件下P (AB )取到最大值，最大值是多少？（2）在什么条件下P (AB )取到最小值，最小值是多少？解：由P (A )=0.6，P (B )=0.7即知AB ≠φ，（否则AB =φ依互斥事件加法定理，P (A ∪B )=P (A )+P (B )=0.6+0.7=1.3>1与P (A ∪B )≤1矛盾）.从而由加法定理得P (AB )=P (A )+P (B )－P (A ∪B )(*)（1）从0≤P (AB )≤P (A )知，当AB =A ，即A ∩B 时P (AB )取到最大值，最大值为P (AB )=P (A )=0.6，（2）从(*)式知，当A ∪B=S 时，P (AB )取最小值，最小值为P (AB )=0.6+0.7－1=0.3。

概率论与数理统计(浙大版)第一章课件

然性, 但在大量试验或观察中, 这种结果的出现具有一定的统计规律性 , 概率论就是研究随机现象规律性的一门数学学科.
如何来研究随机现象? 随机现象是通过随机试验来研究的. 问题什么是随机试验?
8
一、随机试验
在概率论中,把具有以下三个特征的试验称为随机
试验。（1）可以在相同的条件下重复地进行；（2）每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果；（3）进行一次试验之前不能确定哪一个结果会出现。
4
实例2 用同一门炮向同一目标发射同一种炮弹多发 , 观察弹落点的情况.
结果: 弹落点会各不相同.
实例3 抛掷一枚骰子,观结果有可能为: 1, 2, 3, 4, 5 或 6.
察出现的点数.
5
实例4 从一批含有正品
和次品的产品中任意抽取一个产品. 实例5 过马路交叉口时,
其结果可能为:
正品、次品.
则 C A B AB 格”,Ｂ＝“直径合格”．
30
推广称 Ak 为 n 个事件 A1 , A2 , , An 的和事件;
k 1
n
称 Ak 为可列个事件 A1 , A2 , 的和事件.
k 1
n
称 Ak 为 n 个事件 A1 , A2 , , An 的积事件 ;
事件 A 发生事件B 发生
实例 A=“长度不合格” 必然导致 B=“产品不合格” 所以 A B
27
2.事件的相等
若两个事件 A 和B 相互包含，则称这两个事件相等，记为 A .B
A B A =B
A B且B A
A B
A 和 B 同时发生或者同时不发生
28
3.事件的和（并）

浙大概率论与数理统计课件概率论

人们在长期的实践中总结得到“概率很小的事件在一次试验中实际上几乎是不发生的”(称之为实际推断原理)。现在概率很小的事件在一次试验中竟然发生了，因此有理由怀疑假设的正确性，从而推断接待站不是每天都接待来访者，即认为其接待时间是有规定的。
*
§5 条件概率
例：有一批产品，其合格率为90%，合格品中有95%为优质品，从中任取一件，记A={取到一件合格品}， B={取到一件优质品}。则 P(A)=90% 而P(B)=85.5% 记：P(B|A)=95% P(A)=0.90 是将整批产品记作1时A的测度 P(B|A)=0.95 是将合格品记作1时B的测度由P(B|A)的意义，其实可将P(A)记为P(A|S)，而这里的S常常省略而已，P(A)也可视为条件概率分析：
S
A
B
*
事件的运算
S
B
A
S
A
B
S
B
A
A与B的和事件，记为
A与B的积事件，记为
当AB=Φ时，称事件A与B不相容的，或互斥的。
*
“和”、“交”关系式
S
A
B
S
例：设A={ 甲来听课 }，B={ 乙来听课 } ，则：
{甲、乙至少有一人来}
{甲、乙都来}
{甲、乙都不来}
{甲、乙至少有一人不来}
B
A
S
若记P(B|A)=x，则应有P(A):P(AB)=1:x 解得：
一、条件概率定义：由上面讨论知，P(B|A)应具有概率的所有性质。例如：
二、乘法公式当下面的条件概率都有意义时：
*
例：某厂生产的产品能直接出厂的概率为70%，余下的30%的产品要调试后再定，已知调试后有80% 的产品可以出厂，20%的产品要报废。求该厂产品的报废率。

概率论与数理统计课后答案(浙江大学版)

P(
A
B),
P(
A
B),
P(
___
AB),
P[(
A
B)(
___
AB)]
。
解： P(A B) P(A) P(B) P(AB) 0.625，
P(AB) P[(S A)B] P(B) P(AB) 0.375 ，
___
P(AB) 1 P(AB) 0.875 ，
___
P[(A B)(AB)] P[(A B)(S AB)] P(A B) P[(A B)(AB)] 0.625 P(AB) 0.5
每一销售点是等可能的，每一销售点得到的提货单不限，求其中某一
2
概率论与数理统计及其应用习题解答
特定的销售点得到 k(k n) 张提货单的概率。
解：根据题意， n(n M ) 张提货单分发给 M 个销售点的总的可能分法
有 M n 种，某一特定的销售点得到 k(k n) 张提货单的可能分法有
C
k n
6 7 5 4 840 0.0408。
11 12 13 12 20592
9，一只盒子装有 2 只白球，2 只红球，在盒中取球两次，每次任取一只，做不放回抽样，已知得到的两只球中至少有一只是红球，求另
一只也是红球的概率。
解：设“得到的两只球中至少有一只是红球”记为事件 A ，“另一只
也是红球”记为事件 B 。则事件 A 的概率为
P(N1
|
M)
P( N1 )P(M P(M )
|
N1 )
0.6 0.01 0.025
0.24
，
P( N 2
|
M)
P(N2 )P(M P(M )
|
N2)

概率论与数理统计浙江大学第四版课后习题答案 word 完整版

概率论与数理统计浙江大学第四版课后习题答案word 完整版完全版概率论与数理统计课后习题答案第四版盛骤浙江大学浙大第四版(高等教育出版社)第一章概率论的基本概念1.[一] 写出下列随机试验的样本空间(1)记录一个小班一次数学考试的平均分数(充以百分制记分)([一] 1),n表小班人数(3)生产产品直到得到10件正品,记录生产产品的总件数。

([一] 2)S10,11,12,………,n,………(4)对某工厂出厂的产品进行检查,合格的盖上“正品”,不合格的盖上“次品”,如连续查出二个次品就停止检查,或检查4个产品就停止检查,记录检查的结果。

查出合格品记为“1”,查出次品记为“0”,连续出现两个“0”就停止检查,或查满4次才停止检查。

([一] 3)S00,100,0100,0101,1010,0110,1100,0111,1011,1101,1110,1111,2.[二] 设A,B,C为三事件,用A,B,C的运算关系表示下列事件。

(1)A发生,B与C不发生。

表示为: 或A- AB+AC或A- B∪C(2)A,B都发生,而C不发生。

表示为: 或AB-ABC或AB-C(3)A,B,C中至少有一个发生表示为:A+B+C(4)A,B,C都发生,表示为:ABC(5)A,B,C都不发生,表示为:或S- A+B+C或(6)A,B,C中不多于一个发生,即A,B,C中至少有两个同时不发生相当于中至少有一个发生。

故表示为:。

(7)A,B,C中不多于二个发生。

相当于:中至少有一个发生。

故表示为:(8)A,B,C中至少有二个发生。

相当于:AB,BC,AC中至少有一个发生。

故表示为:AB+BC+AC6.[三] 设A,B是两事件且P A0.6,P B0.7. 问1在什么条件下P AB取到最大值,最大值是多少?(2)在什么条件下P AB取到最小值,最小值是多少?解:由P A 0.6,P B 0.7即知AB≠φ,(否则AB φ依互斥事件加法定理, PA∪BP A+P B0.6+0.71.31与P A∪B≤1矛盾).从而由加法定理得P ABP A+P B-P A∪B*(1)从0≤PAB≤PA知,当ABA,即A∩B时PAB取到最大值,最大值为PABPA0.6,(2)从*式知,当A∪BS时,PAB取最小值,最小值为PAB0.6+0.7-10.3 。

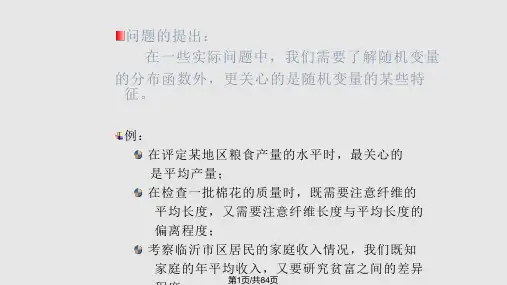
概率论与数理统计(浙大版)第四章课件PPT课件

10
10
10
x
14166.7(元）
第15页/共84页
数学期望的特性：
1.设C是常数，则有E(C) C 2.设X是一个随机变量，C是常数，则有E(CX ) CE(X )
3.设X ,Y是两个随机变量，则有E(X Y) E(X ) E(Y)
将上面三项合起来就是：E(aX bY c) aE(X ) bE(Y) c 4.设X ,Y是相互独立的随机变量，则有E(XY) E(X )E(Y)
其余同理可得，于是Y的分布率为：
期望利润Y 是多少 2？ 0
5 10
pk 0.057 0.205 0.410 0.328
于是 E(Y ) 5.21（ 6 万元）
第6页/共84页
例5：设 X (),求E(X )。
解：X的分布律为：P(X k) ke k 0,1,
k! X的数学期望为：
E( X ) k ke
第1页/共84页
§1 数学期望
例1：甲、乙两人射击比赛，各射击100次，其中甲、乙的
成绩
如下：
甲 8 9 10
次数 10 80 10
乙 8 9 10
次数 20 65 15
解：计算评甲的定平他均成们绩的：成
绩
好
810
坏。
980 100
1010
8
10 100
9
80 100
10
10 100
9
计算乙的平均成绩：
也称为均值(加权均值)。
第2页/共84页
定义：设离散型随机变量X的分布律为：P( X xk ) pk k 1, 2,
若级数 xk pk绝对收敛，则称级数 xk pk的和为随机变量X
k 1

(浙大第四版)概率论与数理统计知识点总结

第1章随机事件及其概率（1）排列组合公式)!(!nmmP n m从m个人中挑出n个人进行排列的可能数)!(!!nmnmC n m从m个人中挑出n个人进行组合的可能数（2）加法和乘法原理加法原理（两种方法均能完成此事）：m+n某件事由两种方法来完成，第一种方法可由m种方法完成，第二种方法可由n种方法来完成，则这件事可由m+n 种方法来完成。

乘法原理（两个步骤分别不能完成这件事）：m×n某件事由两个步骤来完成，第一个步骤可由m种方法完成，第二个步骤可由n 种方法来完成，则这件事可由m×n 种方法来完成。

（3）一些常见排列重复排列和非重复排列（有序）对立事件（至少有一个）顺序问题（4）随机试验和随机事件如果一个试验在相同条件下可以重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验。

试验的可能结果称为随机事件。

（5）基本事件、样本空间和事件在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质：①每进行一次试验，必须发生且只能发生这一组中的一个事件；②任何事件，都是由这一组中的部分事件组成的。

这样一组事件中的每一个事件称为基本事件，用来表示。

基本事件的全体，称为试验的样本空间，用表示。

一个事件就是由中的部分点（基本事件）组成的集合。

通常用大写字母A，B，C，…表示事件，它们是的子集。

为必然事件，？为不可能事件。

不可能事件（?）的概率为零，而概率为零的事件不一定是不可能事件；同理，必然事件（Ω）的概率为1，而概率为1的事件也不一定是必然事件。

（6）事件的关系与运算①关系：如果事件A的组成部分也是事件B的组成部分，（A发生必有事件B发生）：BA如果同时有BA，AB，则称事件A与事件B等价，或称A 等于B：A=B。

A、B中至少有一个发生的事件：A B，或者A+B。

属于A而不属于B的部分所构成的事件，称为A与B的差，记为A-B，也可表示为A-AB或者BA，它表示A发生而B不发生的事件。

概率论与数理统计教学PPT浙大第三版

数据挖掘
02
通过对大量数据进行挖掘和分析，发现数据间的关联和规律，
为人工智能系统的决策提供依据。
自然语言处理
03
自然语言处理中需要进行文本分类、情感分析等任务，需要概
率论与数理统计的知识进行模型训练和优化。
05
概率论与数理统计的未来发展
概率论与数理统计与其他学科的交叉发展
概率论与数理统计与计算机科学的交叉
概率论与数理统计的应用领域
金融
风险评估、投资组合优化、保险精算等。
科学研究
物理、生物、化学、医学等领域的数据分析和实验设计。
工程
可靠性工程、质量控制、系统优化等。
人工智能和机器学习
数据挖掘、模型训练和评估等。
概率论与数理统计的发展历程
概率论的起源
可以追溯到17世纪中叶，当时赌博游戏引发了对概率计算的兴趣。
掌握点估计的概念和方法，如矩估计和最大似然估计。
区间估计
了解区间估计的概念，掌握单个和多个参数的区间估计方法。
估计量的评价准则
了解无偏性、有效性和一致性等评价估计量的准则。
假设检验
假设检验的基本原理
理解假设检验的基本思想、假设的设定和检验步骤。
单个总体参数的检验
掌握单个总体均值、比例和方差的假设检验方法。
概率论与数理统计教学 ppt浙大第三版
• 概率论与数理统计简介 • 概率论基础 • 数理统计基础 • 概率论与数理统计的应用 • 概率论与数理统计的未来发展
01
概率论与数理统计简介
概率论与数理统计的定义
概率论
研究随机现象的数学学科，通过概率模型和随机变量描述随机事件和随机结果。
数理统计

(完整word版)(浙大第四版)概率论与数理统计知识点总结详解

A 不发生的事件。互斥未必对立。 ②运算：结合率：A(BC)=(AB)C A∪(B∪C)=(A∪B)∪C 分配率：(AB)∪C=(A∪C)∩(B∪C) (A∪B)∩C=(AC)∪(BC)
（7）概率的公理化定义
Ai Ai
德摩根率： i1
i1
AB AB，AB AB
设为样本空间， A 为事件，对每一个事件 A 都有一个实数 P(A)，若满足下列三个条件：
件下，事件 B 发生的条件概率，记为 P(B / A) P( AB) 。 P( A)
条件概率是概率的一种，所有概率的性质都适合于条件概率。例如 P(Ω/B)=1 P( B /A)=1-P(B/A) 乘法公式： P(AB) P(A)P(B / A) 更一般地，对事件 A1，A2，…An，若 P(A1A2…An-1)>0，则有
P( A1A2 … An) P( A1)P( A2 | A1)P( A3 | A1A2) …… P( An | A1A2 …
An 1) 。 ①两个事件的独立性
设事件 A 、B 满足 P(AB) P(A)P(B) ，则称事件 A 、B 是相互独立的。
若事件 A 、 B 相互独立，且 P(A) 0 ，则有
A-B，也可表示为 A-AB 或者 AB ，它表示 A 发生而 B 不发生的事件。
1
概率论与数理统计公式（全）
知识点总结
A、B 同时发生：A B，或者 AB。A B=Ø，则表示 A 与 B 不可能同
时发生，称事件 A 与事件 B 互不相容或者互斥。基本事件是互不相容的。
-A 称为事件 A 的逆事件，或称 A 的对立事件，记为 A 。它表示
1
概率论与数理统计公式（全）
知识点总结
当 A=Ω时，P( B )=1- P(B)

浙江大学《概率论与数理统计》课件ch3

1 0.04 0.0375 0.035 0.1125
P ( X i)
0 1 2
P (Y j )
0.80 0.15 0.05 1
16
( 人吸 ) 2 P 患病X 中或 2烟Y P 1 |
P X 1或 2 | Y 1 1 0 .0 3 7 5 0 .0 3 5 P X 0 .0 或 5 Y0 .0 1 13 7 2 | 3 5 0 .6 4 4 0 .6 4 4 4 1 2 5 0 .1 0 .0 3 7 5 0 .1 1 2 5 .0 3 5 0 .6 4 4 4 0 .1 1 2 5
1 2 X 0 解：1 由题意可得： p 0.80 0.15 0.05
P Y 1 | X 0 0 .0 5, P Y 1 | X 1 0 .2 5, P
.2 5, P Y 1 | X 2 0 .7 0
X \Y
0 0.76 0.1125 0.015 0.8875
1
二元随机变量
问题的提出
例1：研究某一地区学龄儿童的发育情况。仅研
究身高H的分布或仅研究体重W的分布是不够的。
需要同时考察每个儿童的身高和体重值，研究
身高和体重之间的关系，这就要引入定义在同
一样本空间的两个随机变量。
例2：研究某种型号炮弹的弹着点分布。每枚
炮弹的弹着点位置需要由横坐标和纵坐标来确
t2
t 1 。试写出 X 1 , X 2的
解： P N t k
e
t
t
k!
k
, k 0 ,1, 2 ,
P X 1 i , X 2 j P X 1 i P X 2 j | X 1 i

浙江大学概率论与数理统计(盛骤第四版)——概率论部分1-90页精品文档

fn ( A )
# 频率反映了事件A发生的频繁程度。
15
n
Ai Ai A1 A2
n
n
An； Ai Ai＝A1A2 An；
i1
i1
i1
i1
例：设A={ 甲来听课 }，B={ 乙来听课 } ，则：
A B {甲、乙至少有一人来}
都不来}
A BAB{甲、乙至少有一人不来}
14
§3 频率与概率
例：

称S中的元素e为基本事件或样本点．
一枚硬币抛一次 S={正面，反面}；记录一城市一日中发生交通事故次数
S={0,1,2,…}；记录某地一昼夜最高温度x，最低温度y
S={(x,y)|T0≤y≤x≤T1}；记录一批产品的寿命x S={ x|a≤x≤b }
10
(二) 随机事件
一般我们称S的子集A为E的随机事件A，当且仅当A所包含的一个样本点发生称事件A发生。例：观察89路公交车浙大站候车人数，S＝{0,1,2,…}；
概率论与数理统计是研究随机现象数量规律的一门学科。
1
第一章概率论的基本概念
• 1.1 随机试验 • 1.2 样本空间 • 1.3 概率和频率 • 1.4 等可能概型（古典概型） • 1.5 条件概率 • 1.6 独立性
第二章随机变量及其分布
• 2.1 随机变量 • 2.2 离散型随机变量及其分布 • 2.3 随机变量的分布函数 • 2.4 连续型随机变量及其概率密度 • 2.5 随机变量的函数的分布
记 A＝{至少有10人候车}＝{10,11,12,…} S， A为随机事件，A可能发生，也可能不发生。
如果将S亦视作事件，则每次试验S总是发生，故又称S为必然事件。为方便起见，记Φ 为不可能事件，Φ 不包含

概率论与数理统计(浙江大学版本)

n! n1!.... nm !
4 随机取数问题例4 从1到200这200个自然数中任取一个,
(1)求取到的数能被6整除的概率
(2)求取到的数能被8整除的概率 (3)求取到的数既能被6整除也能被8整除的概率解:N(S)=200, N(1)=[200/6]=33,
N(2)=[200/8]=25
N(3)=[200/24]=8
30! N (S ) C C C 10! 10! 10!
10 10 10 30 20 10
27! 3! 9! 9! 9! 50 P( A) N (S ) 203
3 C C C P( B) N (S )
7 27 10 20
10 10
一般地，把n个球随机地分成m组(n>m),
要求第 i 组恰有ni个球(i=1,…m)，共有分法：
加法公式：设完成一件事可有两种途径，第一种途径有n1种方法，第二种途径有n2种方法，则完成这件事共有n1+n2种方法。（也可推广到若干途径）
这两公式的思想贯穿着整个概率问题的求解。
有重复排列：从含有n个元素的集合中随机
抽取k 次，每次取一个，记录其结果
后放回，将记录结果排成一列，
n n n

(3) 可列可加性：设A1，A2，…, 是一列两两互不相容的事件，即AiAj＝，(ij), i , j＝1, 2, …, 有 P( A1 A2 … )＝ P(A1) ＋P(A2)+…. 则称P(A)为事件A的概率。 (1.1)
2.概率的性质 P(10-13) (1) 有限可加性：设A1，A2，…An , 是n个两两互不相容的事件，即AiAj＝，(ij), i , j＝1, 2, …, n ,则有 P( A1 A2 … An)＝ P(A1) ＋P(A2)+… P(An); (2) 单调不减性：若事件AB，则 P(A)≥P(B) (3)事件差 A、B是两个事件，则 P(A-B)=P(A)-P(AB)

浙江大学概率论与数理统计盛骤第四版数理统计部分

为什么？
答：只有(4)不是统计量。
17
随机变量独立性的两个定理
定理6.1：设X1, X 2 , , X n是相互独立的n个随机变量，
又设y gi x1, , xni , x1, , xni Rni , i 1, 2, k是k个连续函数，
且有n1 n2 nk n, 则k个随机变量：
[说明]：后面提到的样本均指简单随机样本，由概率论知，若总体X 具有概率密度f(x)，
则样本（X1,X2,…,Xn）具有联合密度函数：
n
fn x1, x2, xn f xi
i 1
16
统计量：样本的不含任何未知参数的函数。
常用统计量：设（X1,X2,…,Xn）为取自总体X的样本
1.
样本均值
n
Yn x
lim P i1 n
n
x
x
证明略。
1
t2
e 2 dt
2
此定理表明，当n充分大时，Yn近似服从N 0,1.
n
即： X（i 近似）～N (n, n 2 ), i＝1
从而，P(a
n i 1
Xi
b)
(b n ) ( a n ).
n
n
答案：N (, 2 )
n
9
定理5.5 德莫佛--拉普拉斯定理
解：设机器出故障的台数为X,则X b400,0.02，分别用三种方法计算：
1. 用二项分布计算
P X 2 1 P X 0 P X 1 1 0.98400 4000.020.98399 0.9972
2. 用泊松分布近似计算
np 400 0.02 8 查表得
P X 2 1 P X 0 P X 1 1 0.000335 0.002684 0.9969

概率论与数理统计 - 浙江大学数学科学学院

在相同条件下重复进行
即每次试验结果互不影响
18

独立重复地抛n次硬币，每次只有两个可能的结果:正面，反面，
P 出现正面 1 2

将一颗骰子抛n次，设A={得到1点}，则每次
试验只有两个结果： A, A,
P A 1 6
从52张牌中有放回地取n次，设A={取到红牌}，则每次只有两个结果： A, A,
称X服从参数p的几何分布
例：从生产线上随机抽产品进行检测，设产品的次品率为p，0<p<1，若查到一只次品就得停机检修，设停机时已检测到X只品，则X服从参数p的几何分布。
38
巴斯卡分布
若随机变量X的概率分布律为
1 r k r P( X k ) Ckr p (1 p ) , k r , r 1, r 2,..., 1

n

e
31
例：某地区一个月内每200个成年人中有1 个会患上某种疾病，设各人是否患病相互独立。若该地区一社区有1000个成年人，求某月内该社区至少有3人患病的概率。
32
解：设该社区1000人中有X 个人患病，则 X P ( X 3) 1 P ( X 0) P ( X 1) P ( X 2 人患病，则 X ~ B(1000, p), 其中p 1/ 200
k 0

c
k 0

k
k!
ce

ce
例：某人骑自行车从学校到火车站，
一路上要经过3个独立的交通灯，设各灯工作独立，且设各灯为红灯的概率
为p，0<p<1，以X表示首次停车时所通
过的交通灯数，求X的概率分布律。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

记（） ij ij i j , ——水平Ai 和水平B j的交互效应, i 1,..., r , j 1,..., s. 易证（） ij 0,
i 1 r
（） 0.
j 1 ij
s
当（） ij＝0对于一切的i 1,..., r , j 1,..., s都成立时，称因子A与因子B对响应无交互作用，否则称有交互作用。当因子A与因子B对响应无交互作用时，模型可写成 X ijk i j ijk , ijk ~ N (0, 2 ), 各 ijk 独立， i 1,..., r , j 1,..., s, k 1,..., t. 称为可加（主）效应模型 r s i 0, j 0. i 1 j 1 4 2 , i , j , 均未知.
5
二、可加效应模型的统计分析
因素A有r个水平A1 , A2 , 因素B有s个水平B1 , B2 , , Ar， , Bs .
现对因素A，B的水平的每对组合( Ai , B j ) i 1,
因素B
, r; j 1,
, s
只作一次试验（此时无法分离交互作用与误差），得到如下结果
因素A
B1
则

i 1
r
i
0,
j 1s来自j 0.7
注意到现在不存在交互作用，故（） i 1,..., r, j 1,..., s. ij 0,
即 ij i j , i 1,..., r, j 1,..., s.
模型可写成 X ijk i j ij , 2 ij ~ N (0, ), 各 ij 独立， i 1,..., r , j 1,..., s. r s i 0, j 0. i 1 j 1 2 , i , j , 均未知.
得到如下结果：
因素B
, r; j 1,
, s
（称为水平组合）都作t (t 2)次试验（称为等重复试验），
因素A
B1
X 111 , X112 , ..., X 11t X 211 , X 212 , ..., X 21t
B2
X 121 , X122 , ..., X 12t X 221 , X 222 , ..., X 22t
当因子A与因子B对响应有交互作用时， X ijk i j （） ij ijk , ijk ~ N (0, 2 ), 各 ijk 独立， i 1,..., r , j 1,..., s, k 1,..., t. 交互效应模型 r s r s i 0, j 0，（）（） ij 0, ij 0. i 1 j 1 i 1 j 1 2 , i , j（ , ） ij , 均未知. 模型可写成
2
设 X ijk ij ijk , ijk ~ N (0, 2 ), 各 ijk 独立， i 1,..., r , j 1,..., s, k 1,..., t. ij , 2均为未知参数.
1 r s 记 ij , ——总平均（一般平均） rs i 1 j 1 1 s 1 r i ij , i 1,..., r, j ij , j 1,..., s, s j 1 r i 1
1 记 ij , ——总平均 rs i 1 j 1
r
s
1 s i ij , i 1,..., r, s j 1 1 r j ij , j 1,..., s, r i 1
i i , ——水平Ai的效应，i 1,..., r , j j , ——水平B j的效应，j 1,..., s.
i i , ——水平Ai的（主）效应，i 1,..., r , j j , ——水平B j的（主）效应，j 1,..., s.
则
r s

i 1
i
0,

j 1
j
0.
3
若上式不成立，
现ij i （）不一定成立 j i 1,..., r, j 1,..., s
§7.4 双因子试验的方差分析
例1 农业生产中需要同时研究肥料和种子品种
对农作物产量的影响。这样的问题就存在两个因
子：一个因子是肥料的种类，一个因子是种子的品种。它们两者同时影响着农作物的产量。 ---双因子试验”。
1
一、双因子等重复试验的统计模型
因子A有r个水平A1 , A2 , , Ar，因子B有s个水平B1 , B2 , , Bs . 现对因子A，B的水平的每对组合( Ai , B j ) i 1,
A1
... ... ... ...
Bs
X 1s1 , X1s 2 , ..., X 1st X 2 s1 , X 2 s 2 , ..., X 2 st
...
Ar
A2
...
...
...
X r11 , X r12 , ..., X r1t
X r 21 , X r 22 , ..., X r 2t
X rs1 , X rs 2 , ..., X rst
X 11
B2
X 12 X 22
A1
... ... ... ...
Bs
X 1s
...
Ar
A2
X 21
...
X r1
...
Xr2
...
X rs
6
X 2s
设 X ij ij ij , ij ~ N (0, 2 ), 各 ij 独立， i 1,..., r , j 1,..., s. ij , 2均为未知参数.

概率论与数理统计-浙江大学数学系.

合集下载