整体微分几何 - 浙江大学数学系
- 格式:doc
- 大小:41.50 KB
- 文档页数:3

浙江大学数学与应用数学专业培养方案培养目标本专业培养学生具有数学科学的基本理论与基本方法,具有扎实的数学基础。
具有良好的数学基础和数学思维能力。
本专业部分课程将为基地班的学生提供独立教学优势,为培养研究人才打下坚实的基础。
该专业毕业生除攻读研究生继续深造外,也可到高校、科研机构、高新技术企业、金融、电信等部门从事数学研究工作与教育、图形图像及信号处理、自动控制、统计分析,信息管理、科学计算和计算机应用等工作。
培养要求主要学习数学与应用数学的基本理论、基本方法,受到计算机和数学软件,数学建模等方面的基本训练。
本专业分为数学与应用数学专业基地班、普通班、运筹学方向三个专业方向,基地班采取滚动制,优秀学生通过选拔可进入基地班,其它两个方向学生可自由选择某一个方向就读。
毕业生应获得以下几方面的的知识和能力:1、掌握数学分析、代数、几何及其应用的基本理论、基本方法。
2、掌握计算机和数学软件及数学建模方面的基本训练。
熟练掌握一门外语。
3、了解数学与应用数学科学的理论前沿、应用前景和最新发展动态。
4、掌握数学与应用数学资料的查询、文献检索及运用现代信息技术来撰写论文,参加学术交流。
专业核心课程数学分析,高等代数,几何学,常微分方程,实变函数,概率论,科学计算教学特色课程外语教学课程:同调代数、整体微分几何、黎曼几何、现代偏微分方程、同调代数、最优化、动态规划、搏弈论自学或讨论的课程:前沿数学专题讨论研究型课程:前沿数学专题讲座计划学制4年最低毕业学分160+4+5授予学位理学学士辅修专业说明辅修专业:23学分,修读带*号的课程;双学位:修读全部专业课程,完成毕业论文。
课程设置与学分分布1.通识课程48学分+5学分见理科试验班类通识类课程2. 大类课程 38.5学分(1)自然科学类≥32.5 学分1)必修课程11门28.5学分。
061B0170 微积分(I) 4.5 秋冬061B0180 微积分(II) 2 春061B0190 微积分(III) 1.5 夏061B0200 线性代数 2.5 秋冬061B0430 普通化学 3 春夏、秋冬061B0421 化学实验(甲) 1.5 春夏、秋冬061B0211 大学物理(甲)I 4 春夏061B0590 地球信息科学基础 2 春夏061B0600 心理学导论 2 秋冬061B0221 大学物理(甲)II4秋冬061B0240 大学物理实验 1.5 秋冬2) 选修课程≥4学分学生可在课程号带“B”的课程中选择修读。

浙江大学数学与应用数学专业培养方案培养目标本专业培养学生具有数学科学的基本理论与基本方法,具有扎实的数学基础。
具有良好的数学基础和数学思维能力。
本专业部分课程将为基地班的学生提供独立教学优势,为培养研究人才打下坚实的基础。
该专业毕业生除攻读研究生继续深造外,也可到高校、科研机构、高新技术企业、金融、电信等部门从事数学研究工作与教育、图形图像及信号处理、自动控制、统计分析,信息管理、科学计算和计算机应用等工作。
培养要求主要学习数学与应用数学的基本理论、基本方法,受到计算机和数学软件,数学建模等方面的基本训练。
本专业分为数学与应用数学专业基地班、普通班、运筹学方向三个专业方向,基地班采取滚动制,优秀学生通过选拔可进入基地班,其它两个方向学生可自由选择某一个方向就读。
毕业生应获得以下几方面的的知识和能力:1、掌握数学分析、代数、几何及其应用的基本理论、基本方法。
2、掌握计算机和数学软件及数学建模方面的基本训练。
熟练掌握一门外语。
3、了解数学与应用数学科学的理论前沿、应用前景和最新发展动态。
4、掌握数学与应用数学资料的查询、文献检索及运用现代信息技术来撰写论文,参加学术交流。
专业核心课程数学分析,高等代数,几何学,常微分方程,实变函数,概率论,科学计算教学特色课程外语教学课程:同调代数、整体微分几何、黎曼几何、现代偏微分方程、同调代数、最优化、动态规划、搏弈论自学或讨论的课程:前沿数学专题讨论研究型课程:前沿数学专题讲座计划学制4年最低毕业学分160+4+5授予学位理学学士辅修专业说明辅修专业:23学分,修读带*号的课程;双学位:修读全部专业课程,完成毕业论文。
课程设置与学分分布1.通识课程48学分+5学分见理科试验班类通识类课程2. 大类课程 38.5学分(1)自然科学类≥32.5 学分1)必修课程11门28.5学分。
061B0170 微积分(I) 4.5 秋冬061B0180 微积分(II) 2 春061B0190 微积分(III) 1.5 夏061B0200 线性代数 2.5 秋冬061B0430 普通化学 3 春夏、秋冬061B0421 化学实验(甲) 1.5 春夏、秋冬061B0211 大学物理(甲)I 4 春夏061B0590 地球信息科学基础 2 春夏061B0600 心理学导论 2 秋冬061B0221 大学物理(甲)II4秋冬061B0240 大学物理实验 1.5 秋冬2) 选修课程≥4学分学生可在课程号带“B”的课程中选择修读。

浙大高等数学教材浙大高等数学教材是一本经典的数学教材,广泛应用于各个高校的数学教学中。
本教材以其严谨的内容、清晰的逻辑以及深入浅出的讲解,深受学生和教师的喜爱。
下面将从教材的概述、章节内容和特点三个方面来介绍浙大高等数学教材。
概述:浙大高等数学教材是由浙江大学数学科学学院编写的教材,首次出版于20世纪50年代。
经过多次修订与完善,至今已经成为了一套全面而系统的高等数学教材。
该教材适用于理工科各个专业的本科生,旨在帮助学生全面掌握高等数学的基本理论与方法,并培养其数学思维与分析问题的能力。
章节内容:浙大高等数学教材涵盖了数学分析、数学代数和数学几何三个主要领域的内容。
其中,数学分析部分主要包括极限与连续、微分学、积分学以及级数与函数项级数等内容。
数学代数部分主要介绍了矩阵与行列式、线性方程组、向量空间、线性变换和特征值等内容。
数学几何部分主要包括向量与空间解析几何、曲线与曲面积分以及曲线与曲面的微分几何等内容。
每个章节都按照递进的顺序进行呈现,从基础概念到深入内容,循序渐进地引导学生掌握数学的基本原理与方法。
特点:浙大高等数学教材的特点之一是其严谨性。
该教材在内容编写上力求精确,逻辑清晰,每个定理都有详细的证明过程,确保学生对每个知识点有深入的理解。
同时,教材中的例题和习题设计也旨在培养学生的问题解决能力和数学思维。
此外,教材还注重理论与实践的结合,通过一些实际问题的引入,使学生能够将数学知识灵活应用于实际生活与科学研究中。
总结:浙大高等数学教材凭借其严谨的内容、清晰的逻辑和深入浅出的讲解而备受好评。
它的编排与内容设置使得学生能够系统地掌握高等数学的理论与方法,并培养其数学思维与问题解决能力。
作为一本经典教材,它对于提升学生的数学素养和培养创新能力有着重要的作用。
无论是作为一名学生还是一名教师,浙大高等数学教材都值得我们的认真学习和借鉴。

整体微分几何整体微分几何是数学中的一个分支,研究的是曲线、曲面以及更高维度的流形的性质和结构。
它通过引入微分形式、度量等工具,对几何对象进行描述和分析。
本文将从整体微分几何的基本概念、主要应用以及发展历程等方面进行论述。
一、基本概念整体微分几何的研究对象是流形,流形是指可以局部地与欧几里得空间同胚的空间。
具体来说,流形是一个拓扑空间,每个点都有一个局部坐标系,使得流形在这些局部坐标系里表现为欧几里得空间。
而整体微分几何的目标是研究流形的曲率、度量以及与它们相关的微分方程等。
在整体微分几何中,微分形式是一个重要的概念。
微分形式是流形上的一个切向量场与对偶空间上的一个切向量场的乘积,并且在切向量场上具有线性性质。
微分形式的引入为整体微分几何提供了一种强大的工具,可以描述曲线、曲面等几何对象的性质。
二、主要应用整体微分几何在物理学、计算机图形学以及其他领域中有着广泛的应用。
其中一个重要的应用是在爱因斯坦的广义相对论中。
广义相对论将引力场看作是时空的弯曲,并用度量张量来描述。
整体微分几何提供了一套工具,可以研究时空的几何结构以及引力的作用。
在计算机图形学中,整体微分几何也有重要的应用。
通过对曲面的描述和分析,可以实现曲面的建模、形变等操作。
例如,曲面的平滑处理、曲率的计算等都是整体微分几何的应用。
除此之外,整体微分几何还在其他领域中得到广泛的应用,如金融学中的风险评估、数据分析中的聚类分析等。
整体微分几何提供了一种用于描述和分析复杂数据的工具,可以帮助人们更好地理解和处理现实世界中的问题。
三、发展历程整体微分几何的发展可以追溯到十九世纪。
其中一位重要的先驱是高斯。
高斯提出了曲率的概念,并通过计算曲率来研究曲面的性质。
同时,黎曼也对流形的几何结构进行了深入研究,并提出了黎曼曲率张量。
这些成果为整体微分几何的发展奠定了基础。
在二十世纪,整体微分几何得到了进一步的发展。
爱因斯坦的广义相对论提出了时空的弯曲概念,并通过引入黎曼度量张量来描述时空的几何结构。

微分流形简介课程号:06191040课程名称:微分流形英文名称:Calculus on Manifolds周学时:3-0 学分: 3预修要求:点集拓扑初步,数学分析,线性代数内容简介:本课程主要包括流形,切问题,张量与外微分形式等概念和一些主要定理,以及流形上的积分和Stokes定理。
通过对本课程的学习,可使学生掌握必要的现代数学基础知识,为学生进一步学习现代数学和近代理论物理,阅读科学论文,进行科学研究打下必要的基础。
选用教材或参考书:白正国沈一兵等编《黎曼几何初步》(前二章)(高教版)《微分流形》教学大纲一、课程的教学目的和基本要求随着近代科学的飞速发展,有关流形,张量及外微分形式,Stokes定理等较现代的知识不仅业已成为数学本身的最基本,最重要且最活跃的研究领域,而且在数学的其他分支中,在力学及物理学(特别是爱因斯坦的广义相对论及规范场论)中,已获得越来越广泛,深刻而富有成效的应用。
今天,流形理论象分析和代数学一样,已不只是某些大学数学系的必修课,而且业已成为其他有关学科的入门学科。
本课程属于大范围分析与几何范畴。
主要论述与流形有关的最重要,最基本的知识,包括流形,切向量,张量与外微分形式等概念和一些主要定理,以及流形上的积分和Stokes定理。
通过对本课程的学习,使学生掌握必要的现代数学基础知识,为学生进一步学习现代数学和近代理论物理,阅读科学论文,进行科学研究打下必要的基础。
二相关教学环节安排1.每周布置作业, 周作业量2~3小时。
2.定期安排习题课,每次1~2学时。
三课程主要内容及学时分配(打▲号为重点讲授部分,打*为选用部分)每周3学时,共17周。
主要内容:(一)欧氏空间的映射1.映射的微分链规则2学时2.反函数定理2学时3.秩定理Sard定理2学时4.习题课1学时(二)多重线性代数1.向量空间对偶空间2学时2.张量积张量代数3学时3.对称和反对称张量2学时4.外代数3学时5.欧氏空间2学时6.习题课2学时(三)微分流形的基本概念1.微分流形的定义2学时*2. 实射影空间Grassmann流形2学时3.流形的映射2学时4.浸入与淹没子流形4学时*5.单位分解2学时6.习题课2学时(四)向量场1.切空间切映射3学时2.切丛向量场3学时3.单参数变换群3学时4.习题课2学时(五)张量场1.张量场2学时2.外微分3学时3.黎曼度量3学时4.习题课2学时(六)流形上的积分Stokes定理1.流形的定向 1.5学时2.带边界流形 2.5学时3.流形上的积分与Stokes定理2学时4.习题课2学时四教材及主要参考书教材:白正国沈一兵等编《黎曼几何初步》(前二章)(高教版)参考书:1.徐森林等编《流形》(高教版)2.米尔诺(Milnor,J.W.) <从微分观点看拓扑>3.斯皮瓦克(Spivak,M.) <流形上的微积分>(科学出版社)4.James R. Munkres, <Analysis on Manifolds>, Addison-Wesley Publishing Company,1991五有关说明本课程所涉及的内容比较抽象, 适宜在数学系基础数学专门化方向的高年级学生中开设。


【必修课】06数学分析(甲I) 06数学分析(甲II) 06数学分析(甲III) 常微分方程(甲)高等代数(I) 高等代数(II) 抽象代数点集拓扑复分析几何学偏微分方程微分几何泛函分析实变函数优化实用算法组合优化数值逼近数值代数微分方程数值解算法语言科学计算数据结构离散数学数据库概率论多元统计分析回归分析数理统计随机过程王秀云人寿保险学现代精算风险理论抽样调查数学规划金融数学多元统计分析【公共课】微积分1 微积分2 微积分3 高等数学常微分方程偏微分方程复变函数与积分变换线性代数课程概率论数理统计随机过程【选修课】测度论抽象代数II 代数几何引论代数拓扑调和分析基础范畴学分形几何环论几何分析引论群论实分析数论导引同伦与同调微分流形小波分析整体微分几何同调代数数学建模数学模型博弈论迭代法的几何理论与方法控制理论基础组合数学最优化操作系统计算机图形学可视化编程技术及其应用软件设计方法微机原理信息学保险精算风险管理计量经济可靠性分析试验设计与分析统计学原理课现代概率论运筹学国民经济统计学货币银行学统计计算与SAS中国顶尖高校王牌专业清华大学:建筑、土木工程,经济管理,机械,力学,计算机、电子信息,核能,协和医科。
北京大学:哲学,经济管理,数学,物理。
北京科技大学:材料、冶金中国人民大学:国际关系,公共管理,法学北京交通大学:铁道运输管理、铁路信号北京师范大学:教育,心理,历史北京外国语大学:外语北京航空航天大学:航空,复合材料、空气动力学、计算机北京理工大学:机械、车辆,爆炸中国农业大学:农业、生物食品中国石油大学:石油天然气,化学化工复旦大学:国际金融政治,经济管理,新闻,数学、生物、微电子华东师范大学:教育,公共管理、心理、地理上海交通大学:船舶海洋,核科学,电气,经济管理同济大学:建筑,土木,桥梁隧道,汽车,德语华东理工大学:石油,精细化工南开大学:文、史,数学,有机化学天津大学:化工、制药、精密仪器,建筑重庆大学:机械设计电机大连理工大学:水工结构,船舶海洋近海工程、化工、物理东北大学:自动化软件、材料、矿山冶金吉林大学:化学、法学,汽车工程,畜牧地质哈尔滨工业大学:航天,机电、材料、环境、计算机南京大学:天文,物理,化学、地学、大气科学东南大学:建筑,土木,道路工程,电子通信南京航空航天大学:航空河海大学:水利,水电南京理工大学:弹药车辆浙江大学:化工、控制、流体传动、计算机、工业心理学、茶学,特种动物中国科技大学:数学,物理,化学,合肥工业大学:汽车、机械厦门大学:金融,历史,会计,化学,近海环境山东大学:文、史,微生物,哲学材料中国海洋大学:物理海洋、海洋生物、药物食品、卫星遥感武汉大学:测绘,病毒科学,计算机软件工程水电华中科技大学:同济医学,光电,电机,模具、新闻中国地质大学:地质,矿产,岩土湖南大学:汽车,机电,工业设计土木国防科技大学:计算机,航天,自动控制,通信指挥中南大学:材料,冶金,医学遗传学,桥梁隧道中山大学:经济管理,光电,生物病害,基因工程、哲学华南理工大学:制糖、造纸,聚合物四川大学:华西医科,生物医学、材料,皮革电子科技大学:电子,信息西南交通大学:电力系统,车辆工程、轨道交通西安交通大学:电气,机械,电子,材料,法医西北工业大学:空气动力,制导,热工程,航空兰州大学:核物理,磁性材料,草地农业。

浙江大学数学与应用数学(英才班)专业培养方案课程设置与学分分布1. 通识课程 48学分+5学分 (1)思政类 5门 11.5+2学分021E0010 思想道德修养与法律基础 2.5 第一学年秋冬 021E0020 中国近现代史纲要 2.5 第一学年春夏 021E0030 毛泽东思想、邓小平理论和“三个代表”重要思想概论 4. 第二学年秋冬 021E0040 马克思主义基本原理概论 2.5 第二学年秋冬 02110081 形势与政策 +2(2)军体类 5.5+3学分031E0010 军事理论 1.5 第一学年秋 031E0020 体育Ⅰ 1.0 第一学年秋冬 031E0030 体育Ⅱ 1.0 第一学年春夏 031E0040 体育Ⅲ 1.0 第二学年秋冬 031E0050 体育Ⅳ 1.0 第二学年春夏 03110021 军训 +2.0 第一学年体育达标+1.0(3)外语类 9学分实行以大学英语Ⅳ考试为标准的管理模式,学生必须通过学校大学英语Ⅳ考试,并取得外语类课程9学分,同时,选修课程号含“F ”的课程,以提高外语水平与应用能力。
(4)计算机类 5学分211G0020 C 程序设计基础与实验 3 第一学年春夏、秋冬 } 任选一门211G0010 C++程序设计基础与实验 3 第一学年春夏、秋冬 211G0030 Java 程序设计基础与实验 3 第一学年春夏、秋冬 211G0040VB 程序设计基础与实验3第一学年春夏、秋冬211G0050 大学计算机基础 2 第一学年秋冬 任选一门 211G0060 计算机技术创新与社会文明 2 第一学年秋冬 以及其他课程号里带“G ”的课程。
(5)导论类 2学分学生可在各专业开设的学科导论课程,以及新生研讨课程中任意选择修读,并取得学分。
(6)其他通识课程 15学分 学生在历史与文化(3学分)、文学与艺术(3学分)、经济与社会(3学分)、沟通与领导(1.5学分)、科学与研究(1.5学分)、技术与设计(3学分)等6个课程组中选择修读。

数学专业学那些课程2楼:课程介绍:高等代数(I)3楼:课程介绍:整体微分几何4楼:课程介绍:微分几何5楼:课程介绍:偏微分方程选讲6楼:课程介绍:组合数学7楼:课程介绍:有限群8楼:课程介绍:微分流形9楼:课程介绍:微分动力系统10楼:课程介绍:调和分析选讲11楼:课程介绍:群表示论12楼:课程介绍:模形式13楼:课程介绍:密码学14楼:课程介绍:李群及其表示15楼:课程介绍:黎曼面16楼:课程介绍:黎曼几何17楼:课程介绍:代数拓扑学初步18楼:课程介绍:常微分方程选讲19楼:课程介绍:拓扑学20楼:课程介绍:实变函数21楼:课程介绍:数学物理方程22楼:课程介绍:解析几何23楼:课程介绍:复变函数24楼:课程介绍:泛函分析25楼:课程介绍:常微分方程26楼:课程介绍:初等数论27楼:课程介绍:抽象代数28楼:课程介绍:高等代数(II)29楼:课程介绍:数学分析课程编号:00132321课程名称:高等代数(I)课程类型:数学科学学院本科生必修课(主干基础课)学时学分:68+34学时,5学分先修要求:无基本目的:1.使学生掌握线性代数的初等部分:线性方程组与矩阵的基本理论,基本方法和基本技巧。
2.培养学生科学的思维方式,提高分析问题和解决问题的能力。
3.渗透现代数学研究结构的观点和分类的思想。
内容提要:1.线性方程组的解法:高斯消去法,线性方程组解的情况,数域。
2.行列式:n元排列,n级矩阵的行列式的定义,行列式的性质,行列式按一行(列)展开,Cramer 法则,Laplace定理。
3.线性方程组的理论:n维向量空间Kn及其线性子空间,线性相关性,基,维数,向量组的秩,矩阵的秩,线性方程组有解判别定理,齐次线性方程组的解空间,非齐次线性方程组的解的结构。
4.矩阵代数:映射,矩阵的运算,常用的特殊矩阵,矩阵乘积的秩,方阵的迹,矩阵的分块,分块矩阵的初等变换,矩阵乘积的行列式,可逆矩阵,求逆矩阵的方法,n 维欧几里得空间Rn,正交矩阵。

《微分几何》课程教学大纲课程名称:《微分几何》课程编码:074112303适用专业及层次:数学与应用数学(本科)课程总学时:72学时课程总学分:4一、课程的性质、目的与任务等。
1、微分几何简介及性质微分几何是高等院校数学和数学教育各专业主要专业课程之一,是运用微积分的理论研究空间的几何性质的数学分支学科。
古典微分几何研究三维空间中的曲线和曲面,而现代微分几何开始研究更一般的空间--流--形。
微分几何与拓扑学等其他数学分支有紧密的联系,对物理学的发展也有重要影响,爱因斯坦的广义相对论就以微分几何中的黎曼几何作为其重要的数学基础。
本课程的前导课程为解析几何、高等代数、数学分析和常微分方程。
2、教学目的:通过本课程的教学,使学生掌握三维欧氏空间中的曲线和曲面的局部微分理论和方法,分析和解决初等微分几何问题,并为进一步学习微分几何的近代内容打下良好的基础。
3、教学内容与任务:本课程主要应用向量分析的方法,研究一般曲线和曲面的局部理论,同时还采用了张量的符号讨论曲面论的基本定理和曲面的内蕴几何内容,并且讨论了属于整体微分几何的高斯崩尼(B公式。
重点让学生把握理解本教材的前二章。
二、教学内容、讲授大纲与各章的基本要求第一章曲线论教学要点:本章主要研究内容为向量分析,曲线的切线,法平面,曲线的弧长参数表示,空间曲线的基本三棱形,曲率和挠率的概念和计算,曲线论的基本公式和基本定理,从而对空间曲线在一点邻近的形状进行研究,同时对特殊曲线特别是一般螺线和贝特朗曲线进行研究。
通过本章的教学,使学生理解和熟记有关概念,掌握理论体系和思想方法,能够证明和计算有关问题教学时数:22学时。
教学内容:第一节向量函数1.1向量函数的极限1.2向量函数的连续性1.3向量函数的微商向量函数的泰勒()公式1.5向量函数的积分第二节曲线的概念2.1曲线的概念2.2光滑曲线、曲线的正常点2.3曲线的切线和法面2.4曲线的弧长、自然参数第三节空间曲线3.1空间曲线的密切平面3.2空间曲线的基本三棱形空间曲线的曲率、挠率和伏雷内公式3.4空间曲线在一点邻近的结构3.5空间曲线论的基本定理3.一6般螺线考核要求:i理解向量函数的极限、连续性、微商、泰勒(L公式和积分等概念,能推导和熟记有关公式,并能使用它们熟练地进行运算。
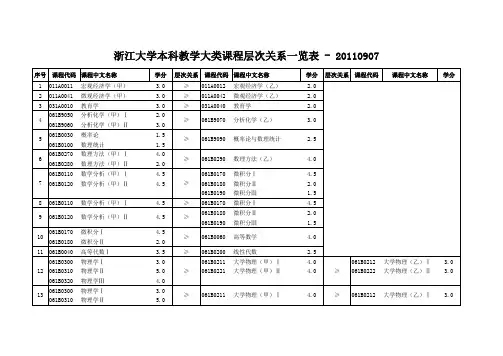
浙江大学本科教学大类课程层次关系一览表 - 20110907
说明:
1.粗线边框内的课程为一个基本单元。
2.符号“≥”为单向关系,表示修读高层次课程后可免修低层次课程。
例如:“011A0011,宏观经济学(甲),
3.0”≥“011A0012,宏观经济学(乙),2.0”表明修读“宏观经济学(甲)”后可以免修“宏观经济学(乙)”,反之不可。
3.符号“≈”为相似关系。
例如:“111Z0040,射频微波通信电路,
4.0”≈“‘11120050,高频电子线路,3.5’+‘11120741,射频与微波电路及其设计,2.0’”表明“射频微波通信电路”和“‘高频电子线路’+‘射频与微波电路及其设计’”中任学一组课程后可免修另一组课程。
4.对于上表中未列出的相近课程,学生申请免修需填写《浙江大学本科课程免修申请表》,经开课院(系)同意后方可免修,申请表可到现代教务管理系统网页下载。
5.其他学院学生及2011年7月前修读电路分析原理或电路分析原理实验的电气学院学生,原则同意进行“电路分析原理”与“电路原理(甲)Ⅰ、Ⅱ”课程的替换;“电路分析原理实验”与“电路原理实验(甲)Ⅰ、Ⅱ”课程的替换。
本科生院教务处
二○一一年九月。
硕士学位论文论文题目 多次数B样条曲线作者姓名 韩敬利 指导教师 汪国昭 教授吴正昌 教授 学科(专业)应用数学所在学院理学院提交日期2007年5月浙 江 大 学申请硕士学位论文多次数B样条曲线作 者:韩敬利学科专业:计算机辅助几何设计与计算机图形学 指导教师:汪 国 昭 教 授浙江大学数学系浙江大学图像图形研究所2007年5月Multi-degree B-spline curvesByHan Jingli(Computer Aided Geometric Design and Computer Graphics)A Thesis Presented toThe Graduated School of Zhejiang University in Partial Fulfillment of the Requirements for theDegree of MasterThesis Supervisor: Professor Guozhao WangDepartment of MathematicsInstitute of Computer Graphics and Image ProcessingZhejiang UniversityHangzhou, P.R. ChinaMay, 2007目录摘要.........................................................................................................Ⅲ Abstract (Ⅳ)第一章 绪论 (1)§1.1自由曲线曲面的发展 (1)§1.2本文研究内容 (4)第二章 多次数B 样条基函数 (7)§2.1多次数样条空间 (7)§2.2准备知识........................................................................................8 §2.3多次数B 样条基函数构造算法 (10)§2.4多次数B 样条基函数性质 (12)第三章 多次数B 样条曲线的构造及其性质 (16)§3.1多次数B 样条曲线的构造 (16)§3.2多次数B 样条曲线的性质 (16)第四章 多次数B 样条曲线的B 样条表示 (20)§4.1 (,)次多次数B 样条曲线 (20)k 1k +§4.2 (,)次多次数B 样条曲线 (23)k 2k +§4.3 (,,k 1k +2k +)次多次数B 样条曲线.. (27)第五章 总结和展望 (28)§5.1本文工作总结...............................................................................28 §5.2未来工作展望. (28)参考文献 (29)致谢 (33)摘要B样条是曲线曲面造型的一个重要工具,但B样条也存在着一定的缺陷.在实际产品设计中,往往会出现一条曲线是不同次数曲线段的连续拼接,B样条方法在表示此类曲线时,相应的控制多边形需要达到一定的要求才能使相应的曲线段退化到设计需要的次数,这样就会使设计过程相对的繁琐且数据储存量大.本文通过得出多次数B样条基函数进而构造多次数B样条曲线.多次数B样条曲线是参数分段多项式表示,且分段次数可以不同.当多次数B样条曲线中各曲线段次数n相同时,曲线退化到B样条曲线.多次数B样条曲线保1nC−连续,其中为相接两段曲线段次数中的较小次数.在应用中多次数B样条曲线更容易表示直线和齿状线,例如只用两个控制顶点就可以表示一条直线段,这就节省了一定量的数据储存.本文首先回顾了计算机辅助几何设计的发展历程,给出了论文的研究背景.本文第二章给出了多次数B样条基函数的构造过程.利用积分迭代的方法得出基函数的表示公式.多次数B样条基函数具有与传统B样条基函数类似的性质,如正性、归一性、局部支柱性等,此外多次数B样条基函数具有次数可异性,在本章中给出了性质的证明.本文第三章给出了多次数B样条曲线的构造过程.多次数B样条曲线同样具有传统B样条曲线的类似的性质,如局部可调性,变差缩减性等,在本章中给出了多次数B 样条曲线的性质的证明.同时给出了一些多次数B样条曲线的应用,用多次数B样条曲线表示能节约一定的数据储存量.本文第四章讨论了曲线多次数B样条表示与其传统B样条表示之间的转换,即两种表示形式的控制多边形的转换关系,并得出从多次数B样条表示到其B样条表示的转换过程是一系列的割角过程,同时本文给出了此割角函数.本文在第五章给出了结论和展望.关键词:计算机辅助几何设计;B样条曲线;多次数B样条基函数;多次数B样条曲线;转换函数;割角AbstractB-spline model is an important modeling tool for CAGD, however it also has certain flaws. In the actual product design, curve is sometimes composed of polynomial segments with various degrees. Using B-spline model to describe this kind of curves, the corresponding control polygon must meet certain requirements, this make the design complex and big storage .In this paper we propose multi-degree B-spline by computing the basis functions for multi-degree B-spline. Multi-degree B-splines are B-spline-like curves that are comprised of polynomial segments of various degrees. Multi-degree B-splines are a generalization of B-spline curves in that if all curve segments in an multi-degree B-spline have the same degree, then it degenerates to a B-spline curve. The curves are at least 1n C−,which n is the smaller of two adjoining curve segments. Multi-degree B-spline curves can easily get cuspid or linear like appearance, when there is a line segment in multi-degree B-spline, we can just use two control points to make it, so multi-degree B-spline model can save some storage.The research background is introduced in the chapter one.The construction of the basis functions for multi-degree B-spline and corresponding proof are given in the chapter two. The basis functions for multi-degree B-spline have some good properties like positivity, weighting, segmented polynomial properties and so on.The construction of multi-degree B-spline curves and corresponding proof are given in the chapter three. Multi-degree B-spline have local support, obey the convex hull and variation diminishing properties. Some applications of multi-degree B-spline curves is discussed in this chapter.The equivalent representation of multi-degree B-spline as “expanded-form” control polygon, which is a conventional B-spline is given in the chapter four. This chapter give the general expressions for the transformation, and also proves that transformation is a series of corner cutting.In the chapter five we draw the conclusion and talk about some prospects.Key words: CAGD, B-spline, the basis functions for Multi-degree B-spline, Multi-degree B-spline curves, transformation, corner cutting第一章绪论计算机的出现给造船、飞机和汽车制造等领域带来了很大的变化,为了利用计算机来帮助解决设计和制造中出现的问题,计算机辅助设计与制造(CAM/CAD)技术应需而生并得到了迅猛的发展.在产品初始设计阶段,描述其外形的曲线或曲面常常只有大致形状或只知道它通过一些空间点列,这类没有数学表达式的曲线或曲面称为自由曲线或自由曲面,CAM/CAD从一开始就与曲线曲面造型技术紧密联系在一起.1974年,Barnhill R.E.和 Riesenfeld R.F.[1]首先提出计算机辅助几何设计一词,简称为CAGD (Computer Aided Geometric Design),用来描述计算机辅助设计(Computer Aided Design)中有关外形的数学方法的研究.自由曲线曲面的表示、设计、显示、分析以及规格、处理(包括数据结构、数据库、图形的信息形式和调整方式等)等问题,是计算机辅助几何设计的主要研究对象和内容.计算机辅助几何设计(CAGD: Computer Aided Geometric Design)作为一个非常有用的曲线曲面造型工具,其首要任务就是建立自由曲线曲面的数学模型,它的产生和发展极大的影响着CAD/CAM 技术的水平.所以随着CAD/CAM 技术的进步CAGD做为一个新的学科开始蓬勃发展,且成为技术革新的重要手段.计算机辅助几何设计是代数几何、微分几何、函数逼近论、计算数学和数控技术的边缘科学.在20世纪60年代典型的曲面表示中,最著名和最实用的是由法国雷诺汽车公司的工程师Bézier提出的Bézier技术和美国机械工程师Coons提出的Coons技术,Bézier、Coons等大师奠定了CAGD的理论基础.之后在工业领域的带动下,20世纪70年代Gordon 和Riesenfeld提出B样条技术,20世纪80年代典型的曲面表示是有理B样条技术.非均匀有理B样条(Non-Uniform Rational B-Spline,简称NURBS)曲线,它兼有B样条曲线形状局部可调性及连续阶数可调的优点,又兼有有理Bézier曲线可精确表示圆锥曲线的特性,所以在1991年国际标准化组织ISO正式把NURBS作为自由曲线曲面的标准数学模型.NURBS作为一种标准为不同的CAD系统之间的数据交换提供了有效的支持.§1.1 自由曲线曲面的发展早在20世纪40年代中期美国数学家I.J.Schoenberg[2]提出了样条函数的概念,尽管当时未引起人们的广泛重视,但对近代样条函数理论和应用的发展有着重大意义.他的研究工作无疑是样条函数发展史上一项奠基工作,但真正奠定CAGD 理论基础的是Bézier 、Coons 等大师.法国工程师Bézier [3]于1962年提出Bézier 曲线系,并根据此理论在雷诺汽车公司建立了著名的UNISURF 自由曲线曲面设计系统[4,5,6].Bézier 方法简单实用,设计员只要移动控制顶点就可修改几何形状,然而在当年Bézier 提出的曲线表达式非常奇特令人难以理解,直到1972年Forrest [7]才提出Bézier 曲线恰好是Bernstein 基与控制顶点的线性组合.一个次的Bézier 曲线由下式定义n 0()()nn i i P t B t p ==∑i 01t ≤≤其中()(1)n i n n i i B t t i −⎛⎞=−⎜⎟⎝⎠t 为Bernstein 基函数,0,1,...,i n =,01...n p p p 称为控制多边形或特征多边形或Bézier 网,简称B 网,(0,1,...,)i p i n =称为控制顶点.早在1974 年,Chaikin [8]提出对多边形割角的方法来产生自由曲线,1980年,Lane 和Riesenfeld [9]把割角方法推广到对空间多边形的所有边每次都同时取中点的递归割角. 割角法的引入使得Bézier 曲线的定义方法简单,几何直观性强.如果把简单割角法改为一般割角法,还可产生B 样条曲线、有理Bézier 等其它自由线.Bézier 方法是一种由控制多边形定义曲线的方法,简单方便、形象直观,只要在空间上定义好控制多边形的形状就可以大致确定曲线曲面的形状,使用户能直观的控制设计对象.但Bézier 曲线也有缺点,它不能精确表示除抛物线外的圆锥曲线,而有理Bézier 曲线既能表示多项式曲线又能表示圆锥曲线,所以它一出现就称为CAGD 的一个研究热点.最早提出并研究应用有理参数曲线的是Rowin [10] , Coons [11],继之有Ball [12], Forrest [13],Farin [14], Pigel [15],刘鼎元[16]等.1964年,美国麻省理工学院机械工程系教授S.A.Coons [17]为设计海军舰艇外形提出了用小块曲面片组合起来表示自由曲面,使曲面片边界连接处可达到任意阶连续的方法,称之为Coons 曲面.其主要思想是把一张复杂的曲面用一定数量的曲面片来表示,适当选择曲面片的数学表达式,然后通过曲面片之间按一定的连续条件拼接,设计过程又能方便地进行修改,增添控制条件以便修改原始曲面,当把附加条件输入计算机时会自动产生新的曲面,直至充分反映设计者意图为止.这种由小曲面片拼接成复杂形状曲面,并可交互设计、修改,达到一定需要精度的交互设计思想是Coons 曲面最早体现出来的曲面设计方法.显然Coons 曲面法对CAGD 的发展有着重要的贡献,是一开创性的工作.Coons 和Bézier 并列被称为现代计算机辅助几何设计技术的奠基人.1974年Gordon 和Riesenfeld [18]把B 样条函数推广到矢值形式得到B 样条曲线.给定参数轴上分割,,用de Boor-Cox 递推公式可得到相应于分割T 的阶B 样条基函数t :{}i i T t ∞=−∞1i i t t +≤k ,()i k N t 1,1,,11,1111[,)()0()()(),2i i i i i k i k i k i k i k i i k i t t t N t t t t t N t N t N t k t t t t ++−+−+−++⎧∈⎧=⎨⎪⎪⎩⎨−−⎪=+⎪−−⎩其他≥ 由于其具有归一性和局部支柱性等特殊性质,使由B 样条基函数表示的样条曲线在造型上有很多好的性质.给定控制顶点列1{}n i i p =,是相应于参数t 轴上分割的阶B 样条基函数,则称,()i k N t :{}i i T t ∞=−∞k ,1()()i ni k i i P t N t p ===∑1(k n t t t +)≤≤为相应于节点向量T 的阶B 样条曲线.以B 样条基函数定义的B 样条曲线是CAGD 中最基本的造型工具之一, 它即具有Bézier 曲线的几何特性,又拥有形状局部可调性及连续阶数可调等Bézier 曲线所没有的特性.把多项式形式的Bézier 曲线向有理多项式推广得到了有理Bézier 曲线,同样把分段多项式形式的非均匀B 样条曲线向分段有理多项式推广可得到非均匀有理B 样条(NURBS)曲线.美国Syracuse 大学的Versprille k [19]在他1975 年的博士论文中首次提出有理B 样条方法. 此后,Piegl 和Tiller [20-27]等人对有理B 样条方法进行了更深入的研究,为非均匀有理B 样条(NURBS)方法打下了坚实的基础.NURBS 曲线兼有B 样条曲线形状可调及连续阶可调的优点,又兼有有理Bézier 曲线可精确表示圆锥曲线的特性,所以在1991年国际标准化组织ISO 正式颁布的工业产品数据交换的STEP 标准中,把NURBS 作为曲线曲面的唯一定义,而国际著名的CAD 软件公司也把造型系统首先建立在NURBS 数学模型上.有理方法固然能解决很多问题但它还是有其固有的缺点,其中不能精确表示螺旋线、摆线等工程上很有用的超越曲线等在实际应用中的缺陷迫切需要解决,于是就催生了一系列B 样条的扩展形式.为了表示螺旋线、摆线等曲线,提出了许多新空间上的基函数.Pottmann [28],张纪文[29-31]提出了一种新型曲线——三次C-曲线,以空间span{, , ,1}代替span{}中幂基构造的曲线.S ânchez-Reyes sin t cos t t 21,,t t [32]研究了三角多项式空间span{1} 的基.Mainar 、Pena 和S ânchez-Reyes ,sin ,cos ,...,sin ,cos t t mt mt t ,...,,sin ,cos n t t t −[33]考虑其他空间,分别在空间span {}、span {,,,,,}、span {1,t ,,,,}中给出了基.这些基函数是随着CAGD 的发展而产生的,它虽然能精确的表示一些B 样条不能表示的曲线,但要表示高阶的自由曲线还是无能为力.2003年,陈秦玉和汪国昭21,,,sin ,cos t t t t 1t sin t cos t sin 2t cos 2t sin t cos t sin t t cos t [34]考虑更一般的情况,在代数和三角多项式混合空间span {}中构造非均匀代数三角(NUAT )B -样条曲线,可以精确表示圆锥螺线和摆线,使得表示高阶的自由多项式曲线的问题得到了解决. 类似与三角多项式空间,Lü和Wang 221,,t t [35]以为基构造代数双曲B -样条(AH B-basis )曲线,能够精确表示一类重要的曲线,例如悬链线与双曲线等.3{1,,...,,sinh ,cosh }n t t t t −在实际设计中经常会出现已有两个曲面的拼接,把两个B 样条曲面拼接为一个B 样条曲面要求这两个B 样体曲面有同样的节点向量,而现实中往往不能满足这一条件,所以在拼接之前先要执行插入节点的操作,而插入节点相应的会增加一列或一行控制顶点,这就大大的加大了操作的数据储存了量,且拼接之后的效果中容易出现裂口需要进一步的弥补.为了解决这一问题,Sederberg [40]提出了T 样条的概念.T 样条理论的依据是PB 样条,PB 样条的控制顶点之间没有拓扑关系,T 样条是建立在T 网格上的PB 样条,则在此基础上插入一个控制顶点不会改变曲面的形状.根据T 样条给出的曲面拼接的方法简单且易于操作.此后Sederberg [41]对T 样条进行了进一步的研究,T 样条逐渐称为一种重要的造型工具.§1.2 本文研究内容前面介绍的B 样条曲线是曲线曲面造型的很好的工具,但B 样条曲线也存在着一定的缺陷.在实际产品设计中,往往会需要一条曲线是不同次数曲线段的连续拼接,在这种情况下如果用B 样条方法表示此类曲线,为了达到设计需求,相应的曲线的控制多边形需要达到一定的要求才能使相应的曲线段退化到设计需要的次数,这样就会使设计过程相对的繁琐.例如需要一条B 样条曲线,在参数分割01{,,...,}n T t t t =中,设计需要曲线在为直线段,在其他参数区间曲线皆为3次曲线,在曲线表示中1[,)i i t t +,41()()i ni i i P t N t p ===∑(其中为控制顶点列,是相应于参数t 轴上分割的4阶B 样条基函数),整条曲线需统一用4阶的B 样条基函数表示,且需要设定1{}n i i p =,4()i N t 321i i i i p p p −−−p ===来使区间1[,)i i t t +上的曲线为直线段,同时在表示当中会出现需用高次基函数来表示低次曲线段的情况,这些都导致了大量几何数据信息的存储.基于解决上述B 样条曲线表示中的问题,本篇文章构造多次数B 样条曲线,多次数B 样条曲线更容易表示直线段和齿状线,比如只用两个控制顶点就可以表示一条直线段,这就节约了数据储存.最初提出构造一条含有不同次数曲线段的样条曲线是应用于保形插值(Costantini,1997,2000[37,38];Kaklis and Pandelis,1990[39]),多次数样条曲线应该说是一个老问题,虽然它在应用上有很多的好处但表达不够直观.随后在多次数样条曲线的概念基础上又提出了多次数B 样条曲线的概念,2003年Sederberg [36]提出了MD-spline 即多次数B 样条的概念,但没有提及多次数B 样条的基函数和构造方法.本文构造了整体曲线的曲线段次数之差不大于2的多次数B 样条曲线的基函数,由此得出构造一条多次数样条曲线的算法.在文献[36]中Sederberg 提出待解决问题之一,就是得到由多次数B 样条曲线转化为其B 样条表示形式的转换函数,并希望得到转换函数的一般表示形式,本篇文章在得出多次数B 样条曲线的基础上解决多次数B 样条曲线转化为相应B 样条表示的问题,并得到转化函数的一般表示且转化过程是割角过程.本文共分五章,各章内容安排如下:第一章:对CAGD 中自由曲线曲面造型技术的发展历程做了综述,并介绍了多次数B 样条曲线的研究背景.第二章:构造了多次数B 样条基函数,并列举了多次数B 样条基函数的性质,如归一性、局部支柱性等,并给出了证明.第三章:讨论了多次数B 样条曲线的构造及性质,并简单介绍了多次数B 样条曲线的应用.第四章:讨论了多次数B 样条曲线与其相应的B 样条表示形式之间的转化,并给出其转化过程就是多次数B 样条控制顶点的重复割角过程,最终得到相应B 样条表示的新的控制顶点列.第五章:全文工作的总结,并展望今后的工作.第二章 多次数B 样条基函数§2.1 多次数样条空间样条是一种特殊的函数,它由多项式分段定义.给定区间[,的一个分割,若函数满足下列两条件:(1)在区间]a b 01:...n a x x x b Δ=<<<=()g x 1[,]i i x x +上,为()g x x 的次多项式;(2) ,即在[,上有直到k 1()[,]k g x C a b −∈()g x ]a b 1k −阶的连续导数;则称是[,上对于分割的k 次样条函数,()g x ]a b Δ(0,1,...,)i x i n =称为样条函数的节点.对于一个给定的节点向量,所有次样条构成一个向量空间,为次样条空间.k k k 次样条空间上一组基函数是次B 样条基函数.给定参数t 轴上分割k :{}i i T t ∞=−∞,,,用下列递推方法所确定的函数称为相应于分割T 的阶即1i i t t +≤0,1,...i =±,()i k N t k 1k −次B 样条基函数的定义1,1,,11,1111[,)()0()()(),2i i i i i k i k i k i k i k i i k i t t t N t t t t t N t N t N t k t t t t ++−+−+−++⎧∈⎧=⎨⎪⎪⎩⎨−−⎪=+⎪−−⎩其他≥l 这里规定,凡是出现0/的的项均为0.上式称为de Boor-Cox 公式,T 称为节点序列或节点向量,称为节点,且若0i t 111...i i i i l i t t t t t −++−+<===<,则称为T 的重节点.B 样条基函数具有很多好的性质,如归一性、局部支柱性等.11,,...,i i i l t t t ++−l 多次数样条同样是由多项式分段定义.给定区间[,的一个分割,若函数满足下列两条件:(1)在不同区间]a b 01:...n a x x x b Δ=<<<=()g x 1[,]i i x x +,1[,]j j x x +(i j ≠)上,分别为()g x x 的次和次多项式,和可以不同;(2),其中为相接两段曲线段次数中的较小次数;则称是[,上对于分割的多次数样条函数,对于一个给定的节点向量和对应每个节点区间的次数,多次数样条构成一个向量空间,为多次数样条空间.k l k l 1()[,]n g x C a b −∈n ()g x ]a b Δ当给定节点向量,对应每个节点区间的曲线段次数均相等时,多次数样条曲线即为样条曲线.§2.2 准备知识下面介绍构造多次数B 样条基函数的准备知识.本篇文章中只考虑整体曲线各曲线段次数之差不大于2次的变次数B 样条曲线,为了构造多次数B 样条曲线的基函数的需要,下面给出0次、1次和2次的初始函数和平移函数的定义.初始函数均定义在节点向量上. 011{,,...,,}n n T t t t t −=定义1: 零次初始函数在节点向量上设节点区间的两端点皆为单节点,定义零次初始函数T 10,01()0i i i t t t I t +≤<⎧=⎨⎩其他 如图(1)所示图(1):零次初始函数定义2: 一次初始函数令节点区间的两端点皆为两重节点.在节点向量上定义一次初始函数T 22111,011/()/0i i i i i i i i i t t t t t t t 2i i I t t t t t t t t ++++++−−≤<⎧⎪=−−≤<⎨⎪⎩其他+图(2):一次初始函数定义3: 二次初始函数令节点区间的两端点皆为三重节点,定义二次初始函数2233222221211,02211()/()2()()/()()()/()0i i i i i i i i i i i i i i i t t t t t t t t t t t t t t t t I t t t t t t t t +++++++++++⎧−−≤<⎪−−−≤<⎪=⎨−−≤<⎪⎪⎩其他32i i ++如图(3)所示图(3):二次初始函数定义4: 平移函数j I在上面给出的三种初始函数的定义中,节点重数都是同为1重、2重或者3重,但在构造多次数B 样条曲线基函数的过程中节点重数并不要求具有同样的重数.为了基函数构造过程的需要,本文给出一个函数的定义,此函数用来平移一个基函数的定义区间,记此函数为j I ,其中j 表示平移区间的个数.下面给出了平移函数对于三种不同次数初始函数的作用效果10,01()0i j i ji j t t t I t I +++≤<⎧+=⎨⎩其他22111,011/()/0i j i j i j i j i j i j i j i j i ji i t t t t t t t I t I t t t t t t t +++++++++++++++−−≤<⎧⎪+=−−≤<⎨⎪⎩其他22233222221211,02211()/()2()()/()()()/()0i j i j i j i j i ji j i j i j i j i j i ji j i j i j i j i j i j t t t t t t t t t t t t t t t t I t I t t t t t t t +++++++++++++++++++++++++++++⎧−−≤<⎪−−−≤<⎪+=⎨−−≤<⎪⎪⎩其他32§2.3多次数B 样条基函数的构造算法因为在实际的设计当中,参数的范围往往被限定在一个有限区间如[,上,在多次数B 样条基函数的构造过程中,不妨令参数定义在一个有限区间上.当给定区间[,的一个参数分割(t ]a b ]a b 011{,,...,,}n n T t t t t −=1,0,1,...,1i i t t i n +<=−),给定每个节点区间对应的曲线次数即对应节点向量T 的次数列011{,,...,}n K k k k −=,其中对应节点区间的曲线次数为,基于本文的限定,这些次数之差必须小于3即1[,)i i t t +i k 3i j k k −<(),记曲线次数中的最小次数为k 即,0,1,...,1i j n =−min()k K =,则每个节点区间对应的曲线次数相应的可表示为j j k k r =+,其中为0、 1或2的正整数. (0,1,...,1)j r j n =−下面给出多次数样条曲线基函数的构造算法1) 确定各区间初始基函数的次数,分别为(0,1,...,1)j r j n =−.2) 插入重节点.此处规定不同次数相接处的节点重数按右边区间的次数确定.根据前面给出的初始基函数的定义,0次基的区间端点节点的重数设为1,1次基的区间端点节点的重数设为2,2次基的区间端点节点的重数设为3.插入重节点后节点向量为,其中'''''011{,,...,,}m m T t t t t −=012...2n m n r r r r 1n −−=+++++.为了保持端点插值性,初始节点我们设为重,则起始端点处节点为,同样终止节点我们设为,终止端点处节点为 .01k r ++0'''10{,...,,,...,}k t t t t −−'r +m k +11n k r −++1''''1{,...,,,...,}n m r m m m k t t t t −−+3) 利用2.1节准备知识在节点向量上定义初始基函数.''''''01{,...,,,...,,...,}k m T t t t t t −=Step1.初始化, (0i =,0()0j B t =01,1,...,...1n j k k r r n k −=−−+++++−) Step2.得到初始基函数for()0;;j j n j =<++Step2.1 for()0;1;j s s r s =<+++0,01,0,02,0()0()()()s i j s i s ij s i j I t I r B t I t I r I t Ir +⎧+⎪=+⎨⎪+⎩= =1=2End-for Step2.2 i i s =+ End-forStep3. 得到多次数B 样条基函数for(01;...1;n j k j r r n k j −=−<+++−++),11,1,,11,1()()()[]tj k j k j k j k j k B s B s B t d σσ−+−−+−−∞=−∫ s其中,,()j k j kBt dt σ+∞−∞=∫,如果,()0j k B t =则定义,,()10tj k j k j kB s t t j m ds σ+−∞>≤⎧=⎨⎩∫如果且 其他End-for例如,在节点向量01234{,,,,}T t t t t t =上,曲线在各个参数区间上所需的次数要求如下图所示1次 2次 1次 3次图(4) 可知曲线段中最小次数为1,则令1k =按照算法第一步,确定各个参数区间初始基函数的次数,对应各个参数区间由左往右分别为零次、一次、零次、二次.然后按照每个参数区间上初始基函数的次数来得到新的节点向量,如下图所示'T图(5)在节点向量上按照算法构造相应的初始基函数,如下图所示'T图(6)§2.4 多次数样条基函数的性质多次数B 样条基函数具有类似与B 样条基函数的性质.性质3.1 归一性:.,()1i k iB t =∑证明:当时由初始基函数的定义显然成立,0k =,0()1i iB t =∑.不妨设在非零区间上非零的初始基函数为1[,)r r t t +,0j B ,,(2次初始基函数),或1,0j B +2,0j B +,0j B ,(1次初始基函数),或1,0j B +,0j B (0次初始基函数),由基函数的积分公式 ,11,1,,11,1()()[]ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫积分次后,则在区间上非零的基函数对应上述三种情况分别为k 1[,)r r t t +,j k k B −,1,j k k B −+,,...1,j k B −,,j k B ,1,j k B +,2,j k B +,或,j k k B −,1,j k k B −+,,...1,j k B −,,j k B ,1,j k B +或是,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B .则在区间上根据基函数的积分公式可得1[,)r r t t +,11,1,,,11,1()()()()tmmi k i k i k i k i j ki j k i k i k B s B s B t B t σσ−+−=−=−−+−−∞==−∑∑∑∫ds整理后可得,11,1,,11,1()()()tmj k k m k i k i j kj k k m k B s B s B t d σσ−−+−=−−−+−−∞=−∑∫s 2其中对应初始基函数的三种情况,1,m j j j =++,又根据基的定义可知在区间上为零,1,1m k B +−1[,)r r t t +,1j k k B −−的非零区间为1[,)a r t t −,其中为a t ,0j k B −非零部分所在区间的起始端点节点,所以,1,1,,1,1()()()1()j k k mj k k i ki j kj k k j k k Bt dtB s Bt ds Bt dtσ+∞−−+∞−−−∞+∞=−−−−∞−−−∞==∫∑∫∫= 性质得证. 性质3.2 线性无关性证明:由基的定义可知当时是线性无关性成立,根据归一性的证明,同样不妨设在任一非零区间上,假设当0k =1[,)r r t t +1n k =−时基函数线性无关即当且仅当.现设,11()0mi i k i j k a B t −=−+=∑0(1,...,)i a i j k m ==−+,()0mii ki j ka Bt =−=∑,由算法中基函数的积分公式,11,1,,11,1()()[ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫可得到,()mi i k i j ka B t =−=∑,11,1,11,1()()tmi k i k ii j ki k i k B s B s a d σσ−+−=−−+−−∞−∑∫s整理后得,()mi i k i j ka B t =−∑,1,1()tj k k j kj k k B s a ds σ−−−−−−∞=∫11,1()tmi i i j k i k a a σ−=−+−−∞−+∑∫,1()i k B s ds −1,11,1()tm k mm k B s a d σ+−+−−∞−∫s在区间上,在基函数的归一性证明中可知1[,)r r t t +,1,1()1tj k k j k k B s ds σ−−−−−∞=∫,1,11,1()0tm k m k B s ds σ+−+−−∞=∫,所以,()mi i k i j ka B t =−∑j k a −=+11,1()tmi i i j k i k a a σ−=−+−−∞−∑∫,1()i k B s ds −.把,r t t =12r t t t +r+=两种情况带入上式可得0(,...,)i a i j k m ==−,由数学归纳法性质得证.性质3.3 正性:此性质的说明见第四章.性质3.4 次数可异性:由基函数的构造方法可知. 性质3.5 局部支柱性证明:当时,在非零区间上非零的初始基函数只有0k =1[,)r r t t +,0j B ,,(2次初始基函数),或1,0j B +2,0j B +,0j B ,(1次初始基函数),或1,0j B +,0j B (0次初始基函数).由基函数的积分公式,11,1,,11,1()()[ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫k 积分次后,可以得到在区间上非零的基函数只有1[,)r r t t +,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B ,1,j k B +,2,j k B +,或,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B ,1,j k B +或是,j k k B −,1,j k k B −+,.,..1,j k B −,,j k B 分别与上述三种初始基函数的情况对应,性质得证.性质3.6 当给定曲线每个曲线段次数相同时,变次数B 样条基函数即为B 样条基函数.性质3.7 求导公式:()(1)(1),,1,11,1()()/()/r r r i k i k i k i k i k B t B t B t σσ−−−−+−+−=−1,1证明:由基函数积分公式,11,1,,11,1()()[ti k i k i k i k i k B s B s B ds σσ−+−−+−−∞=−∫求导可得.第三章 多次数B 样条曲线的构造及其性质§3.1 多次数B 样条曲线的构造利用上一章所定义的基函数,可以得到整个参数空间上的多次数B 样条曲线. 不妨设参数定义在一个有限区间[,上,给定区间[,的一个参数分割(]a b ]a b 011{,,...,,}n n T t t t t −=1,0,1,...,i i t t i n +1<=−)和对应节点区间的曲线段次数列,根据第二章算法可得到对应的多次数B 样条基函数10:{}n i i K k −=,k k B −,,…,1,k k B −+,m k B ,其中,,同样由基函数的定义可知min()k K =10(1)(1)n i i m n k k −==−−∑1,s k B +,…,,m k B ,在参数区间上恒为零,其中,所以在区间上有非零定义的基函数为11(n i i s n k k −==−+−∑),k k B −,,…,1,k k B −+,s k B ,可以定义样条空间上的曲线如下,()()sj kj j kP t Bt p =−=∑其中是控制顶点, ,(,...,)j p j k s =−3i p R ∈1...k k s p p −−+p 是控制多边形或控制网格,整条曲线保阶连续,两段曲线相接处保1k C −1n C −连续,其中为相接两段曲线段次数中的较小次数.n 由于本篇文章只讨论曲线中各曲线段次数差不大于2的多次数B 样条曲线,所以我们给出此类多次数B 样条曲线的记法.如果多次数B 样条中含有,和次曲线段,我们记这条曲线为次多次数B 样条曲线,如果只含有和次曲线段,我们把曲线记为次多次数B 样条曲线,同样如果只含有和次曲线段,我们把曲线记为次多次数B 样条曲线.k 1k +2k +(,1,2)k k k ++k 1k +(,1)k k +k 2k +(,2)k k +§3.2 多次数B 样条曲线的性质与B 样条曲线类似,多次数B 样条曲线具有以下性质:。
苏步青——我国微分几何研究的开拓者著名数学家(1902-)谷超豪苏步青,数学家,数学教育家。
早年执教于浙江大学,后长期担任复旦大学领导工作。
研究领域涉及仿射曲面理论,射影曲线一般理论,曲面的射影微分几何理论等,获许多优秀成果。
在计算几何及其应用方面颇多建树。
是我国微分几何研究的开拓者之一。
苏步青1902年9月23日出生于浙江省平阳县带溪村。
父亲苏宗善,靠种地为生。
童年的苏步青已学会做些辅助劳动,割草、喂猪、放牛等活儿都干过。
由于家境贫寒,不能上学读书,他靠自己找书看,《水浒》、《聊斋》等名著不只读过一遍。
每当放牛回家路过村上私塾,他总要凑上去偷听一阵。
父亲眼看儿子如此好学,终于决定节衣缩食,在他9岁时送他上学。
1915年8月,苏步青考取温州市浙江省立第十中学,1919年7月中学毕业,赴日本留学进东亚日语预备校学习。
第二年3月,以第一名成绩考入东京高等工业学校电机系。
1924年,又以第一名成绩考进东北帝国大学数学系。
1927年发表第一篇学术论文,同年入本校研究生院当研究生并兼任教员。
1931年1月在东北帝国大学获得理学博士学位,3月偕夫人松本米子(后加入中国籍,改名苏松本,以毕生精力支持苏步青的事业)回国。
60年来他一直为中国的数学事业和教育事业奋斗不息,取得了辉煌的成就,受到数学界和全国人民的敬仰和爱戴。
学术上的重大成就苏步青的研究方向主要是微分几何。
1872年,德国数学家F.克莱因(Klein)提出了著名的“爱尔兰根计划书”,在其中总结了当时几何学发展的情况,认为每一种几何学都联系一种变换群,每种几何学所研究的内容就是在这些变换群下的不变性质。
除了欧氏空间运动群之外,最为人们所熟悉的有仿射变换群和射影变换群。
因而,在19世纪末期和本世纪的最初三四十年中,仿射微分几何学和射影微分几何学都得到很迅速的发展。
苏步青的大部分研究工作是属于这个方向的。
此外,他还致力于一般空间微分几何学和计算几何学的研究。
数学专业考研方向详解及院校推荐基础数学:基础中的基础专业轮廓数学本就是基础学科,基础数学更是基础中的基础。
它的研究领域宽泛,理论性强。
主要是指几何、代数(包括数论)、拓扑、分析、方程学以及在此基础上发展起来的一些数学分支学科,具体的分支方向包括:射影微分几何、黎曼几何、整体微分几何、调和分析及其应用、小波分析、偏微分方程、应用微分方程、代数学等。
凯程考研集训营保录班,是全日制封闭式高三式,成立于2005年4月,是我国最早从事高端全科保过辅导的正规培训机构,由英语名师索玉柱教授、政治李海洋教授为代表的教研组组成。
被学员一致公认业界授课质量最好,服务最到位,应试效果最显著。
凯程教育以“专业、负责、创新、分享”的办学理念,突出“高命中率、强时效性、全面一条龙服务”的特色,成为考研学子选择专业课辅导的首选。
九年来已有千余位考生在凯程的帮助下顺利考取北大、清华、人大、北师大、中传等全国著名高校,引发业界强烈关注。
凯程考研集训营作为考研精品辅导的领航者,可以很自信的讲在业内始终保持着最高的考研上线率,一次性的上线率(含A、B线)已经接近95%。
最大亮点:与其他机构不同,凯程考研集训营是名师小班授课的全日制考研特训机构,凯程考研集训营对英语、数学、政治都有被实践检验了的独一无二的教研和系统的方法。
按高分计划辅导要求学员,在法学、法硕、金融、医学、艺术等专业具有压倒性的专业课辅导优势和经验,在清华、北大、人大、中传具备核心的院校资源和优势;优势专业和优势院校奠定了凯程考研集训营的高端品质。
机具个性化的辅导方案:入学测试+每日测验+每周小测+每周计划+每周计划完成情况全部载入档案袋,详细掌握每一位学员的学业进展;根据学员细致的情况指导今后每一步的学习和10月份的志愿报考。
有考研择校问题,对考研复习不熟悉的地方,请联系凯程咨询老师。
学长点拨Tobia(2007级计算机博士生,基础数学方向):基础数学在国际上一直备受关注,取得了不少重大的研究成果,但遗憾的是在国内的发展尚不及其他4门更偏向应用的二级学科。
整体微分几何简介
课程号:06191440
课程名称:整体微分几何英文名称:Global Differential Geometry
周学时:3-0 学分:3
预修要求:微分几何(局部理论)
内容简介:
《整体微分几何》主要介绍曲线与曲面的大范围整体几何性质,包括某些拓扑性质。
内容分四章:第一章介绍活动标架法,它是研究整体微分几何和几何分析的有力工具。
第二章介绍3维欧氏空间中闭曲线的整体微分几何性质。
第三章介绍3维欧氏空间中曲面的整体微分几何性质。
第四章介绍曲面的内蕴几何。
通过本课程学习,使学生掌握整体微分几何的基本概念和重要思想方法,了解数学各方向之间相互交织、相互渗透的现代数学概貌。
选用教材或参考书:
《整体微分几何初步》沈一兵编着浙江大学(原杭州大学)出版社 1998
《整体微分几何》教学大纲
一、课程的教学目的和基本要求
随着现代数学的发展,整体微分几何已成为核心数学的一个重要组成部分。
为了使数学专业的大学生具备较高的数学素质,有必要让他们了解这方面的基本内容和思想方法。
通过对《整体微分几何》的学习,使学生初步掌握整体微分几何的基本概念和重要思想方法,学会简单的外微分计算和活动标架法,了解有关整体曲线和整体曲面的著名定理和重要公式,以及它们的证明主要思路。
要求学生通过本课程学习,了解数学各方向之间相互交织、相互渗透的现代数学概貌,为今后进一步深造打下扎实基础。
二、相关教学环节安排
1.采用课堂讲授和课外作业,强调启发式教学。
2.每周讲课3学时。
每周布置作业,作业量1-2学时。
主要针对基本概念和解问题的思路。
三、课程主要内容及学时分配(打▲号为重点讲授部分)
每周3学时,共17周。
主要内容:
(一)外微分与活动标架法10学时1.幺正标架3学时
2.外微分形式▲3学时
3.可积系统2学时
4.曲面论的活动标架法2学时(二)曲线的整体微分几何 14 学时1.平面曲线的某些整体性质▲ 7学时
2.空间曲线的某些整体性质▲ 7学时
(三)E3中曲面的整体微分几何 21 学时1.曲面的Gauss-Bonnet公式 3学时
2.球面的刚性定理▲ 3学时
3.凸曲面与积分公式▲ 3学时
4.全平均曲率与Willmore猜想▲ 3学时
5.常负曲率曲面与Backlund变换▲ 3学时
6.极小曲面的Bernstein定理▲ 3学时
7.常平均曲率曲面 3学时(四)曲面的内蕴几何 6学时1.向量场与指标定理▲ 3学时
2.完备曲面与Hopf-Rinow定理 3学时
四、教材及主要参考书
教材:《整体微分几何初步》沈一兵编著浙江大学(原杭州大学)出版社 1998 主要参考书:(1)《微分几何》苏步青、胡和生等编著高等教育出版社 1984
(2)《黎曼几何初步》白正国、沈一兵等编著高等教育出版社 1992
五、有关说明
为了讲课方便,可以先讲(二)曲线的整体微分几何,然后讲(一)外微分与活动标架法。
此外,(三)中各节内容相对独立,可以不必按此顺序讲授。