i第九章传递函数模型

传递函数模型和传递函数传递函数是控制系统中一个重要的概念，它描述了输入信号经过系统后的输出信号与输入信号之间的关系。

传递函数模型是用来描述连续时间系统的，而传递函数是传递函数模型的具体表达式。

传递函数模型可以简化对系统行为的分析和设计。

通过将系统抽象为一个传递函数，可以忽略系统的具体细节，只关注输入输出之间的关系。

这样一来，我们可以用数学方法来分析系统的稳定性、性能等特性。

传递函数模型通常用拉普拉斯变换来表示。

拉普拉斯变换是一种数学变换，用于将连续时间域中的函数转换为复频域中的函数。

通过拉普拉斯变换，可以将微分方程转化为代数方程，从而简化对系统的分析。

传递函数通常表示为H(s)，其中s是复变量，表示频域中的频率。

传递函数的形式可以是分数形式，如H(s)=N(s)/D(s)，其中N(s)和D(s)分别是多项式。

传递函数的分子多项式N(s)描述了输入信号对系统的影响，而分母多项式D(s)描述了系统的特性。

传递函数的分母多项式D(s)的根决定了系统的稳定性。

如果分母多项式的根都是负实数或者有负实部的复数，那么系统是稳定的。

反之，如果分母多项式的根有正实数或者纯虚数，那么系统是不稳定的。

传递函数还可以用来描述系统的频率响应。

频率响应描述了系统对不同频率输入信号的响应程度。

通过传递函数，可以计算出系统在不同频率下的增益和相位差。

传递函数模型和传递函数在控制系统的分析和设计中起着重要的作用。

通过传递函数模型，可以对系统进行数学建模和分析。

而通过传递函数，可以计算系统的稳定性、频率响应等特性。

掌握传递函数模型和传递函数的使用方法，对于控制系统的工程师来说是非常重要的。

总之，传递函数模型和传递函数是控制系统分析和设计中常用的工具。

通过传递函数模型，可以对系统进行简化和抽象，忽略系统的具体细节。

而通过传递函数，可以计算系统的稳定性、频率响应等特性。

掌握传递函数模型和传递函数的使用方法，可以帮助我们更好地了解和设计控制系统。

传递函数建模
传递函数建模是一种将系统的输入与输出之间的关系表示为传递函数的方法。

传递函数（Transfer Function）描述了输入信号与输出信号之间的数学关系，在控制系统中常用于分析系统的动态行为和进行系统设计。

传递函数建模的步骤如下：
1. 系统分析：首先对待建模的系统进行分析，了解系统的输入输出关系。

可以通过实验、观察或数学建模等方法来获取系统的输入输出数据。

2. 建立数学模型：根据系统的输入输出关系，建立系统的数学模型。

传递函数通常是用拉普拉斯变换表示的，可以将系统的输入输出关系表示为一个分子多项式除以一个分母多项式的形式。

3. 参数估计：确定传递函数的参数。

有时候，系统的参数可以通过实验测量得到，或者通过理论分析进行估计。

4. 评估模型：对建立的传递函数模型进行评估，比较模型的输出与实际系统的输出之间的差异，调整模型的参数以提高模型的拟合度。

5. 使用模型：使用建立的传递函数模型进行系统分析和设计。

传递函数可以用于分析系统的稳定性、频率响应、阶跃响应等性能指标，同时也可以用于设计控制器或者滤波器。

总之，传递函数建模是一种对系统进行数学建模的方法，通过建立数学模型来描述输入输出关系，从而分析系统的动态行为和进行系统设计。

传递函数模型与干预变量分析时间序列真的仅仅受本身滞后值影响吗？在单变量时间序列中，我们假设系统输出仅仅受既往值和随机干扰项的影响。

但实际应用中，可能还有其他与之相关的时间序列，那么如何将其它的变量引入时间序列模型是一个值得讨论的问题。

设y表示某种商品在一段时间的销售额，由于经济时间序列通常有记忆性，可以用一个ARMA模型来t描述其变化规律，假定其变化规律的表达式为1 / 10110.46t t t y y ε-=+但是在许多实际情况下，销售额不仅仅受自己滞后值1t y -的影响，还会受其它一些输入变量的影响。

我们考虑广告费t x ，广告费对销售额的影响不仅具有即期影响还具有一定的滞后效应，假定其滞后的影响是一期，那么在上式中就应加入广告费的当期和滞后一期的值，如果广告费的即期影响效用是0.55，滞后一期值对销售额的影响效用是0.60，则这个简单的输出和输入关系为110.460.600.55t t t t t y y x x ε--=+++如果上式是一个适应的模型，那么该模型t 时刻的输出由三个部分组成，系统1t -时刻的值1t y -，,1t t -时刻输入的t x 和1t x -，以及与前两部分相互无关的随机扰动项t ε。

如果我们用后移算子B ，可以将模型写成()(10.46)0.550.60t t t B y B x ε-=++则模型可以写成0.550.60110.4610.46t t t B y x B Bε+=+--。

这样的模型有什么统计特征，又如何定阶、估计和诊断呢？本讲专门讨论多维时间序列建模的相关问题，但是又与我们通常了解的向量自回归不同，这里一定有一个自变量和若干个解释变量。

内容结构为：首先引入了传递函数模型，并讨论了传递函数模型和脉冲响应函数的基本特征和性质，脉冲响应函数与互相关函数的关系以及传递函数模型的稳定性。

在此基础上介绍了传递函数模型的识别、估计和诊断，并用通过实例分析说明建模的过程。

自动控制原理传递函数
自动控制原理传递函数是描述控制系统输入输出关系的数学模型，通常以s域传递函数的形式表示。

在控制系统中，输入信
号经过传递函数的作用，产生输出信号。

传递函数是由系统的微分方程所得到的拉普拉斯变换得到的。

控制系统中的传递函数通常是指示系统的输入与输出之间的关系，称为开环传递函数。

在控制系统中，传递函数是通过将系统的微分方程进行拉普拉斯变换得到的。

传递函数可以用来分析系统的动态性能，并通过调整传递函数的参数来改善系统的稳定性、快速性和准确性。

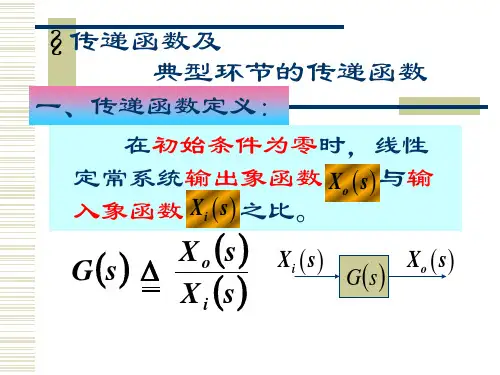
传递函数通常用以下形式表示：
G(s) = Y(s) / U(s)
其中，G(s)是传递函数，Y(s)是输出信号的拉普拉斯变换，U(s)是输入信号的拉普拉斯变换。

传递函数描述了输入与输出信号之间的关系，以及系统对输入信号的响应速度和稳定性等性能。

控制系统设计中，可以根据给定的性能要求，选择合适的传递函数来实现所需的控制效果。

常见的传递函数包括比例传递函数、积分传递函数、微分传递函数以及它们的组合。

通过对传递函数进行数学分析和计算，可以得到系统的稳定性、频率响应、步跃响应等性能指标。

控制系统设计师可以根据这些指标来优化系统的性能，并进行参数调整和改进。

总之，传递函数是自动控制原理中非常重要的概念，它描述了控制系统输入与输出之间的关系。

通过分析和优化传递函数，可以实现控制系统的稳定性、准确性和快速性等性能要求。

传递函数模型函数模型建模方法是一种用于解决定量数学优化问题的统一框架，也被称为单层规划或模型结构理论。

函数模型建模方法把优化问题表示成函数模型，然后由优化算法来求解这些模型。

下面是函数模型建模方法的相关内容：一、函数模型的外部表示1、表示目标：函数模型建模方法将优化问题表示成满足一组约束条件下函数最优化的问题，即将求解结果用函数表示。

2、设定变量：函数模型将问题内容用变量表示出来，并将相关变量限制在一定的范围，然后确定最优解所需要的变量范围。

3、设定函数：目标函数需要设计一个具有较强解释性的目标函数，然后根据目标函数构建函数模型。

4、设定约束：确定相关的约束条件，约束条件可以是硬约束也可以是软约束，用来限制求解最优解的自由度。

二、函数模型的内部表示1、逐步回溯：函数模型主要是考虑每一步回溯动作所带来的后果，并以此形成正解或最优解。

2、约束调度：主要考察约束的类型，有硬约束和软约束，根据实际情况，以最优化任务为目标，决定是否采取相应的调度方法。

3、解析算法：这类算法通过解析函数模型实现最优解的求解，所考虑的算法有贪婪算法、非贪婪算法等。

4、搜索算法：该类算法也可以实现最优解的求解，此类算法主要有模拟退火算法、遗传算法、模糊算法、粒子群优化算法等。

三、函数模型建模方法的优势1、计算速度快：函数模型建模方法可以实现快速求解，而传统网络模型建模、代数模型建模需要耗费大量时间。

2、收敛性好：因为函数模型拥有收敛性，所以可以有效降低求解过程中因数值误差而造成的误差。

3、可控性强：函数模型的求解过程可以有效控制，可以根据实际需求调整参数使求解过程更加简单有效。

4、适用范围广：函数模型几乎可以适用于任何领域，即使对求解过程比较复杂，也可以应用函数模型来解决。

传递函数模型传递函数模型是多变量时间序列分析模型这种模型表示的经济系统是用多个时间序列描述的。

例如，研究某企业的销售额依时间变化的规律，不仅考虑销售额疗;列本身，而且研究促销活动，例如广告费，把销售额序列看作因变量序列即系统的输出，广告费支岀看作自变量序列即系统的输人。

两序列之间通过传递因子产生联系，建立传递函数模型。

此种模型兼备了时间序列和因果关系的功能，充分描绘了广告促销活动对销售额变化产生的影响。

一、传递函数分析模型设表示经济系统的输出序列例如某企业的销售额，是我们研究的U标变量，是因变量表示系统的输人序列(例如广告费支出)，是解释变量是噪声变量，表示其它变量影响的组合。

那么，系统的传递函数模型可以表示为v(B)=呦+巧B +巾B? +…"(B)是一个算子多项式，B是一个后移算子；称脉冲响应权或传递函数权；是一个均值为零、方差固定而且与独立的随机变量。

x“Xz在模型中部件时解释变量，而且在时间上对来说是一个先行指标，即对的影响将提前k个时期。

算子多项式u(B)有无穷多项，在某些一般性的条件下，可用算子B的两个有理多项式之比来估计u(B) ,即这里o)(B) = -(0[B ------ a)s B s= -------------- “O对这两个多项式均要求他它们的根在单位圆外，也就是要求它们是平稳的。

这样，传递函数模型可写为6)(8)其中不一定是白噪声，但已假定它是同&独立的，因而可以用ARIMA模型去表示它，即%满足d 。

⑻g丽5这里是白噪声，是d阶连续差分算子。

= 1 ——••• —(ppB»V(B)0(B)满足平稳可逆条件。

因此传递函数模型乂可写为3(B) “ v 9(B)记则有3(8) &⑹y厂丽冷"+丽实际的建模运算绝不需要对每个变量施以同样的差分运算，差分的阶数只需使变量达到平稳即可。

上式为一般的传递函数模型，可用下图表示。

该模型可以推广到含m个解释变量的情形上式看起来十分复杂，但它的一些特殊情况，已是我们早已熟悉的模型。