下载文档原格式
控制系统的传递函数定义
控制系统传递函数是描述控制系统输入与输出关系的数学模型，通常用于分析和设计控制系统。
它表示了输入信号经过控制系统后的输出信号，可以用数学公式表示为输出信号Y(s)与输入信号U(s)的关系：Y(s)=G(s)U(s)。
其中，G(s)为系统的传递函数，它是一个复数函数，描述了控制系统的动态特性和稳态特性。
传递函数的分母描述了系统的阻尼和自然频率，分子描述了系统的增益和相位，通过对传递函数进行分析可以得到系统的稳态误差、稳定性、响应速度等性能指标。
因此，传递函数是控制系统分析和设计的重要工具，对于掌握控制系统的动态特性和优化系统性能具有重要意义。
- 1 -。
可编辑修改精选全文完整版控制系统的数学模型及传递函数2-1 拉普拉斯变换的数学方法拉氏变换是控制工程中的一个基本数学方法，其优点是能将时间函数的导数经拉氏变换后，变成复变量S的乘积，将时间表示的微分方程，变成以S表示的代数方程。
一、拉氏变换与拉氏及变换的定义1、拉氏变换：设有时间函数，其中，则f(t)的拉氏变换记作：称L—拉氏变换符号；s-复变量； F(s)—为f(t)的拉氏变换函数，称为象函数。
f(t)—原函数拉氏变换存在，f(t)必须满足两个条件(狄里赫利条件)：1)在任何一有限区间内，f(t)分断连续，只有有限个间断点。
2)当时，，M，a为实常数。
2、拉氏反变换：将象函数F（s）变换成与之相对应的原函数f(t)的过程。
—拉氏反变换符号关于拉氏及变换的计算方法，常用的有：①查拉氏变换表；②部分分式展开法。
二、典型时间函数的拉氏变换在实际中，对系统进行分析所需的输入信号常可化简成一个成几个简单的信号，这些信号可用一些典型时间函数来表示，本节要介绍一些典型函数的拉氏变换。
1．单位阶跃函数2．单位脉冲函数3．单位斜坡函数4．指数函数5．正弦函数sinwt由欧拉公式：所以，6．余弦函数coswt其它的可见表2-1：拉氏变换对照表F(s) f(t)11(t)t三、拉氏变换的性质1、线性性质若有常数k1，k2,函数f1(t),f2(t),且f1(t),f2(t)的拉氏变换为F1(s),F2(s),则有：，此式可由定义证明。
2、位移定理(1)实数域的位移定理若f(t)的拉氏变换为F(s),则对任一正实数a有, 其中，当t<0时，f(t)=0，f(t-a)表f(t)延迟时间a. 证明：，令t-a=τ,则有上式=例：, 求其拉氏变换(2)复数域的位移定理若f(t)的拉氏变换为F(s),对于任一常数a,有证：例：求的拉氏变换3、微分定理设f(t)的拉氏变换为F(s),则其中f(0+)由正向使的f(t)值。
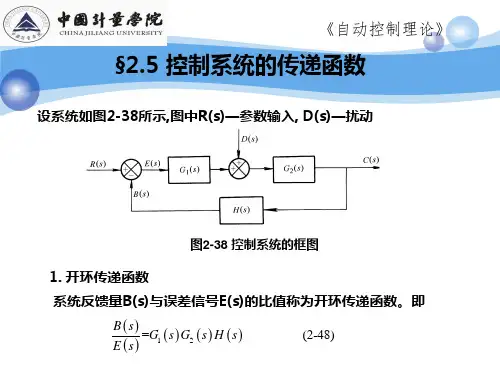
控制系统的传递函数考虑扰动的闭环控制系统X i (s )到X o (s )的信号传递通路称为前向通道；X o (s )到B (s )的信号传递通路称为反馈通道；1.闭环系统的开环传递函数将闭环控制系统主反馈通道的输出断开，即H (s )的输出通道断开，此时，前向通道传递函数与反馈通道传递函数的乘积G 1(s )G 2(s )H (s )称为该 闭环控制系统的开环传递函数。
记为G K (s )。
闭环系统的开环传递函数也可定义为反馈信号B (s )和偏差信号ε (s )之间的传递函数，即：2..x i (t )作用下系统的闭环传递函数令n (t )=0，此时在输入x i (t )作用下系统的闭环传递函数为：输入作用下系统的偏差传递函数 令n (t )=0，此时系统输入X i (s )与偏差ε (s )之间的传递函数称为输入作用下的偏差传递函数。
用)(s i εΦ表示。
3.n (t )作用下系统的闭环传递函数令x i (t )=0，此时在扰动n (t )作用下系统的闭环传递函数（干扰传递函数）为：扰动作用下系统的偏差传递函数，令x i (t )=0，此时系统在扰动作用下的偏差传递函数（称扰动偏差传递函数）。
)()()(1)()()()()(212101s H s G s G s G s G s X s X s i i +==Φ)()()(11)()()(21s H s G s G s X s s i i i +==Φεε)()()(1)()()()(21202s H s G s G s G s N s X s N +==Φ)()()(1)()()()()(212s H s G s G s H s G s N s s N N +-==Φεε。
