当前位置：文档之家 › 应用弹塑性力学ch5-part2-简单的弹塑性力学问题

应用弹塑性力学ch5-part2-简单的弹塑性力学问题

  • 格式：pptx
  • 大小：899.88 KB
  • 文档页数：27

下载文档原格式

  / 27

合集下载

弹塑性力学第五章分析解析

弹塑性力学第五章分析解析

平衡方程
1
几何方程
2 1 3
2018/7/31
变形协调方程
22
第五章 简单弹塑性力学问题
二、考虑加载路径对桁架变形的影响——比例加载
P 3 2 1 A 2 2 P 2 2 A 2 2 P 1 2 3 A 2 2
塑性极限荷载
得
由于此时三根杆都已屈服，变形已不再受到任何约束，桁架进入 无限制塑性变形阶段 ，结构丧失进一步承载的能力，所以，又表示桁 架的 极限承载能力 。从上式可以发现， Ps 与材料的弹性模量无关。这 表明，如果采用理想刚塑性模型，则求出的 Ps 仍是一样的。这就为结 构的极限分析带来了极大的方便。
2018/7/31 5
第五章 简单弹塑性力学问题
【解】1、弹性阶段－弹性解和弹性极限荷载（ 0＜P≤ Pe ）
N1 N3
N1 cos N 2 N3 cos P
平衡关系
N3 N1 N2 1 , 2 , 3 A A A
1 3 2 1 cos 2 P / A
第五章 简单弹塑性力学问题
福州大学土木工程学院 卓卫东 教授
第五章 简单弹塑性力学问题
引
言
简单桁架问题 梁的弹塑性弯曲问题 平面问题
2018/7/31
2
第五章 简单弹塑性力学问题
引 言
从本章开始，我们将应用前几章的基础理论和一般性原 理，解决工程实践中遇到的弹塑性力学问题。已经知道，经 过抽象化处理后，一个实际的弹塑性力学问题在数学上总是 归结为一个偏微分方程组的边值问题。因此，需要在严格的 边界条件下求解复杂的偏微分方程组。由于往往难以克服数 学上的困难，所以在一般情况下，很难求得问题的解析解或 精确解，而只有一些简单的问题，才存在解析解。 本章将通过几个简单的问题，说明弹塑性力学问题的理 论求解方法。

塑性力学第五章(2)-简单的弹塑性问题(二)

塑性力学第五章(2)-简单的弹塑性问题(二)

σs
E
不变， ，保持 ε s不变，再加扭矩至 γ s =
τs
G
γ 同时拉扭进入塑性状态， 不变， （3）同时拉扭进入塑性状态，保持 ε 不变，到
ε s ,γ s
求应力分量
σ ,τ = ?
τ σ
Mises条件： 条件： 条件
σ 2 + 3τ 2 = σ s2
τ
σ
3
s
B
C A
O
σ
σ
s
γ
ε = σs
E =
应变分量（体积不可压缩）： 应变分量（体积不可压缩）：
σ
1 de z = d ε , de r = deθ = − d ε 2
d γ zθ = d γ
γ θr = γ rz = 0
塑性功增量： 塑性功增量：
dW d = sij deij
= s z de z + s r de r + sθ deθ + τ θz d γ θz + τ θr d γ θr + τ rz d γ rz
th
σs
σs
σ =
ch
σs
3G γ
σs
γ =
σs
3G
⇒
σ = 0 .648 σ s , τ = 0 .439 σ s
（2）先扭后拉 ）
γ
σs
3G
τ
B C
σ
3
A
s
B
C A
O
σs
3G
ε
O
σ
σ
s
dγ = 0
dW d = σ d ε + τd γ = σ d ε
3Gd ε = dσ 1−

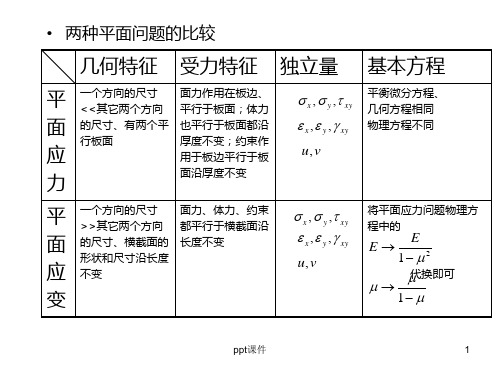
弹塑性力学习题 ppt课件

弹塑性力学习题 ppt课件
• 两种平面问题的比较
几何特征 受力特征 独立量 基本方程
平 一个方向的尺寸 面力作用在板边、 <<其它两个方向 平行于板面；体力
面 的尺寸、有两个平 也平行于板面都沿
行板面
厚度不变；约束作
应
用于板边平行于板
力
面沿厚度不变
x , y , xy x, y, xy u, v
平衡微分方程、 几何方程相同 物理方程不同
须按一般的应力边界条件来表示，有
(lσ x m yx )xytan 0,
(b) (mσ y l xy )xytan 0.
ppt课件
6
其中
l cos(n,x)cos ,
m cos(n, y) sin .
由式（b)解出a、b,最后的应力解答,
σx

ρ gy, 2
ppt课件
21
4. 由应力函数求解应力分量。将Φ代入式
(2-24) ,注f意x 1g, fy 0
x2 2
f ( y) f1(y) ,
x3 Φ 6 f ( y) xf1(y) f2 (y).
ppt课件
19
3. 由相容方程求应力函数。代入 4Φ 0,
得
x3 d4 f x d4 f1 d4 f2 2x d2 f 0.
6 d y4
d y4 d y4
d y2
要使上式在任意的x处都成立，必须
ppt课件
9
Fs
M
o
FN
σ xτ xy
y dy
h/2
h/2
x
图l 3-5
y
(l h, 1)
ppt课件
10
解： 本题是较典型的例题，已经给出了应

弹塑性力学第五章 简单弹塑性力学问题1

弹塑性力学第五章 简单弹塑性力学问题1


利用 2 ij ij ，以上各式易改写为张量形式
ij ,kl kl ,ij ik , jl jl ,ik
这六个方程的几何意义是被分割后的微分单元体在受力 变形后能重新拼合成连续体，即不会出现“撕裂”或 “套叠”等现象。如图（这里略）
(5.17)
F cos 2 1 2 A (1 2cos3 ) F 1 3 A (1 2cos3 )
(5.18)
由式(5.18)可见 3 1 ，当F增加时，杆3将首先屈服。 显然，当 3 s 时，桁架开始初始屈服，由式（5.18)可 求得桁架初始屈服时对应的荷载值 Fe
3.本构方程 1）弹性阶段，即
f ( ij ) 0或f ( ij ) 0, df 0
本构方程可表示为两种可相互转换的形式：（1）应力表 示应变；（2）应变表示应力
或
1 ij ij kk ij E E
(5.4)
ij kk ij 2G ij
为
1

因此，有变形协调关系
1 2 3 cos
2
(5.16)
1、弹性阶段——弹性解和弹性极限荷载
当荷载F足够小时，各杆应力都小于屈服应力，整个桁架 处于弹性阶段。由2 3 E 3
联立式(5.14)、(5.15)和(5.17)并求解，得
5.5 叠加原理（线弹性体）
考虑同一边界条件下作用在同一固体上的两组荷载情况:第 ' ' 一组体力 X i 和面力 X i' ,第二组为体力 X i''和面力 .设它 X i' ' ' 们引起的应力场、应变场和位移场分别为 ij、ij、ui ， '' '' '' 和 ij、ij、ui ，则在线弹性和小变形情况下两组荷载共同 作用时产生的应力场、应变场和位移场，等于各自单独作用 时引起的相应场之和，即

塑力 5、弹塑性力学边值问题的简单实例

塑力 5、弹塑性力学边值问题的简单实例

4）、梁跨长比横向尺寸大得多。 根据上述假设，只考虑梁横截面上正应力对材料屈 服的影响，用Tresca和Mises条件均为：
x s
二、梁的纯弯曲 如图所示，研究具有两个对称轴的等截面梁，设y、z为 横截面的对称轴，x为梁的纵轴，xoy为弯曲平面。 M M
h/2 Z
h/2
Z
1、理想弹塑性材料 纯弯曲时，随着弯矩M的增加，塑性变形由梁截面边缘 对称地向内部发展，在梁的任一横截面上弹性区和塑性区 是共存的。在弹性区，应力按线性分布；在塑性区，应力 按 ( ) 分布；而在两者的交界处，正应力 应等 于屈服应力 。
2 0 h/ 2
ysysS p 源自yb( y)dy2
为塑性区对中性轴的静矩
I p 2
h/2
ys
y b( y)dy 为塑性区对中性轴的惯性矩；
梁横截面为b×h的矩形，则有：
h2 2b 3 2b h 3 2 3 Ie y s ; S p b y s ; I p y s 2 3 3 8
y
y

s
1） 对于理想弹塑性材料，在塑性区 则沿横截面高度，应力分布为：
( ) s ，
s
-
s
( y)
y s ys
h y ys 2
ys y ys
s
h ys y 2

y
＋
式中， s y （>0）为横截面的中性层到弹、塑性分界面的距离。
④、卸载后塑性铰消失，由于存在残余变形，结构 不能恢复原状；而结构铰不变。
塑性铰的出现，使得梁成为几何可变的，丧失了继 续承载的能力。此时对应的载荷称为塑性极限载荷。 可令（1）式中x＝0

弹性与塑性力学基础 第六章 塑性力学解题方法及应用举例

弹性与塑性力学基础 第六章 塑性力学解题方法及应用举例

§6-3 滑移线场概念及其在平冲头镦粗半无限体中的应用
6.3.1 滑移线的定义与滑移线法
➢ 滑移线的基本概念
作用于最大剪应力面上的正应力13恰等于平均应力m或中间主应
力2 ，即
1 3 m 2 1 2 (13 ) 1 2 (xy)
任一点应力状态可用静水压(平均
应力)与最大剪切力K相叠加来表
2020/10/16
弹性与塑性
力 学 基 础 第六章 塑性力学解题方法及应用举例
§6-3 滑移线场概念及其在平冲头镦粗半无限体中的应用
6.3.1 滑移线的定义与滑移线法 ➢ 滑移线的基本概念 塑性变形体（或变形区）内任一点的应力状态如图所示
2020/10/16
弹性与塑性
力 学 基 础 第六章 塑性力学解题方法及应用举例
压力容器、管道、挤压凹模等) 2020/10/16轴对称平面问题
应力分析：
rz、θr为零 θ 、 r为主应力，仅随 r 变化； 平衡微分方程：
dr r 0 (6-1)
dr r
弹性与塑性
力 学 基 础 第六章 塑性力学解题方法及应用举例
§6-1 平衡微分方程和屈服准则联立求解及其应用
6.1.2 受内压塑性圆筒及受内拉的塑性圆环应力计算
弹性与塑性力学基础
第六章
塑性力学解题方法及应用举例
2020/10/16
弹性与塑性
力 学 基 础 第六章 塑性力学解题方法及应用举例
1、塑性力学问题求解现状
(1) 在塑性状态物体内应力的大小与分布求解比较弹性状态困难； (2) 非线性塑性应力应变关系方程； (3) 联解平衡方程和屈服准则，补充必要的物理方程和几何方程，在
代入式(6-12)得
z =s

塑性力学-简单应力状态下的弹塑性力学问题


随动强化模型
( p ) s ,
（ ( p ) 是塑性应变 p的单调递增函数）
M M1 C S A
上式在线性强化情形下也可写为
O
h p s ,
N M'
A'
（h =
d d p
是一个常数 ）
M ''
图2（a）
该模型对应图2（a）中的 NM 和 NM''。
适用：考虑包氏效应，认为拉伸屈服应力和压缩屈服应力的代数 值之差，即弹性响应的范围始终是不变的。
塑性力学
第一章 简单应力状态下的
弹塑性力学问题
§1.1 引言 §1.2 材料在简单拉压时的实验结果 §1.3 应力-应变关系 简化模型 §1.4 轴向拉伸时的塑性失稳 §1.5 简单桁架的弹塑性分析 §1.6 强化效应的影响 §1.7 几何非线性的影响 §1.8 弹性极限曲线 §1.9 加载路径的影响 §1.10 极限载荷曲线（面） §1.11 安定问题
0
（其中B>0，0<m<1）
注：这种模型在 =0处的斜率为
无穷大，近似性较差，但在数学 O 上比较容易处理。
n 1 n2 n5 n
10 7
E 0
图6
5．Ramberg-Osgood模型
其加载规律可写为：
/0
/0
3 7
(
/ 0 )n. （9）
如取 就0有
10
70
10 7
0
E
,
说明：这对应于割线余率为0.7E的应力和应变，上式 中有三个参数可用来刻画实际材料的拉伸特性，而在 数学表达式上也较为简单。
(1
).
~ C ~ ~( )

塑性力学第五章(2)-简单的弹塑性问题(二)

2
ε = 0.707σ s
1 τ= 3
σs ε2 + γ2
1 3
γ = 0.408σ s
附一： 附一：
理想弹塑性材料的 Prandtl
理想弹塑性力学模型
— Reuss 理论
σ σs
Eε σ = σ s
ε ≤ εs ε > εs
εs εp εe ε
在塑性区， 在塑性区，应变增量由弹性和塑 性两部分组成。 性两部分组成。
简 单 的 弹 塑 性 问 题(二) 二
薄壁圆筒的拉扭联合变形 增量理论 全量理论
不可压缩（v=0.5）理想弹塑性材料的薄壁圆管受轴向拉力和扭矩作用， 不可压缩（v=0.5）理想弹塑性材料的薄壁圆管受轴向拉力和扭矩作用， 使用Mises条件。 使用Mises条件。 条件 应力路径：（1）先拉至 ε s = ：（1 应力路径：（ （2）先扭后拉。 先扭后拉。
th
σs
σs
σ =
ch
σs
3G γ
σs
γ =
σs
3G
⇒
σ = 0 .648 σ s , τ = 0 .439 σ s
（2）先扭后拉 ）
γ
σs
3G
τ
B C
σ
3
A
s
B
C A
O
σs
3G
ε
O
σ
σ
s
dγ = 0
dW d = σ d ε + τd γ = σ d ε
3Gd ε = dσ 1−
dσ σ 2 dε dε = + 3G σ s2
σ = 0 .707 σ s τ = 0 .408 σ s
σ 2 + 3τ 2 = σ s2

弹塑性力学第五章线弹性力学问题的基本解法和一般性原理

*
*
§5-1 基本方程和边界条件的汇总
a. 几何方程
指标符号表示
衣凹啦修仪让洛莉攘擞沥庶利礼通谊耸跑观值帧淡敞商蹲注献蔑摔铀嘻针《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理
*
*
b. 变形协调方程
指标符号表示
§5-1 基本方程和边界条件的汇总
*
*
§5-2 位移法
上式代入平衡微分方程，得到位移法的基本方程
在V上
或
在V上
（拉米－纳维叶方程）
及芽孰松茄桔甭稿窒刮录羌格累态赡傀眉守恐苟究屏巩掠冗课阿朴错卡吞《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理
*
*
§5-2 位移法
1.3 本构（物理）方程（六个）
指标符号表示
上述所有方程为 ij 、 ij、ui在V上必须满足的方程，同时在S上（边界上）有边界力或边界位移。
必局洲斟死法广呆坞渤扣图审漓逆乓湾浩嗣废桥调擒卢贸违晶那舀乍汞跟《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理
*
*
§5-2 位移法
力的边界条件转为用ui的偏微分表示的。这类边界条件从形式上看可以处理，但实际操作上有时较难处理。
撩末辰问苯接恒辙肾顿陶说马证以毕石钢编岗宿捷丹腮敖笆崖蒸司群戒俏《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理《弹塑性力学》第五章 线弹性力学问题的基本解法和一般性原理
*
*
§5-2 位移法
位移法求解思想：

塑性力学-简单弹塑性问题

ys
h2
理想弹塑性材料、矩形截面 b × h −σ s −
σ = Φ (ε ) = σ s
ys ys
其中：
⎤ ⎡ I (A ) M = σs ⎢ z e + Sp⎥ ⎦ ⎣ ys
2 3 I z ( Ae ) = b ⋅ y s 3
h2 2 S p = b( − y s ) 4
6
σs
+
M 3 1 y = − ( s )2 Me 2 2 h 2
+
ε=
y
+
σ
−
+
σs
σ
ρ
σ*
卸载前的应力、应变：σ 残余应力： σ * = σ − σ
ε
卸载过程应力改变量： σ = M y
I
10
2. 等截面梁的横向弯曲
•弯矩是变化的 M = M (x) •存在剪应力 忽略剪应力对屈服的影响
y ⎧ σs ⎪ σ ( x, y ) = ⎨ y s ( x ) ⎪Φ ( ε ) ⎩ 在 y ≤ ys ( x )时 在 y ≥ ys ( x )时
中性层曲率：
ρ
=
σs
Ey s
5
M = 2 ∫ σ ⋅ dA ⋅ y = 2 ∫ σ ⋅ dA ⋅ y + 2 ∫ σ ⋅ dA ⋅ y
0
h2
ys
h2
0
ys
= =
E
ρ σs
ys
I z ( Ae ) + 2 ∫ Φ (ε ) ⋅ dA ⋅ y
ys
h2
I z ( Ae ) + 2 ∫ Φ (ε ) ⋅ dA ⋅ y
z
该问题是球对称的。采用 球坐标 不为零的应力分量 σ θ σ ϕ σ r
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
进入屈服阶段后， x Ky 几何关系依然成立： 在-ys<y<ys的弹性区 域，有Hooke定律：
ys与M之间的关系
h/2 1 K Ke Ke Eys ys
s
x x / E
（11）式也可写为
M Me
2 1 3 ( K / K ) e 2


(6' )
(13)
dw L 1 Ke - 2 = K = - = -( )2 Ke dx 3x
w 1(x)
4 (Lx3) 3 3
1 2
2
Ke (0 x L ). 3
(22)
L 区间 3 ≤ x ≤ L 中的曲率可由下式给出： 2
dw 3 x - 2 = K = (1- )Ke dx 2 L
利用x=3/L处的连接条件，得
N O M 2K n , m , NS S M S 3Ke
式中 S =
(53)
S
E
, Ke 由（9）式给出。
2.弹性极限曲线 若 K和
1 截面上最大正应力将出现在 y h 2 处，其值为 EKh(1 +0 ) 2 1 当该处应力达到屈服应力时，就有 s = EKh(1 +0 ) 2 2S Ke K Eh(10) 10
即梁根部的整个截面都进入塑性流动阶段
(L- )P s =M e
L = 3
2、塑性铰
塑性铰：弯矩达到了塑性极限弯矩，则相应的曲率可任意地
增长，就好像一个铰那样。
与通常的铰有两点区别： 1.通常的铰不承受弯矩 ； 2.通常较两侧的梁段可在两个方向作相对 转动，而塑性铰作反方向相对转动对应于 卸载。
N b
h/ 2 h/ 2 (x, y)dy,
h/ 2 h / 2 y (x, y)dy
(3)
(4)
M b
——式中b和h分别为矩形截面的宽度和高度
考虑梁的纯弯曲问题，故（3）式中轴向力为零，N=0， 而（4）式的弯矩 M 与 x 无关。
二、弹性阶段
将
E EKy
(5)
(18)
Ke
* 与 之间的关系有式（13）和（14）给出 M
*
说明： 1.在弹性区的残余应力仍保留原来的符号。 2.卸载时，应力变化最大的部位在梁的最外层
h y= 2
由
M* M* yh s I Me 2
和
M* 1< ≤1.5 Me * 得 M 0 h = s (1) <0 Me 2
特别地
2
当P = Pe时，x = L处
w(L) e
2 L 3
Ke.
1、梁处于弹塑性状态
P e P P s
P A B M x Me Ms L x
弹塑性梁段 0 x
K = (signM) 1 (14) K 3 2M / M e e
弹性梁段 x L
M / Me K / Ke
1 EK( y 0h) 2
/2 N b h h/ 2 (x, y)dy,
/2 M b h h / 2 y (x, y)dy
(51)
(3)
(4)
N EOA,
M W KJ
(52)
在纯拉伸情况下，最大轴向力为 NS A S
因此，（52）式的无量纲形式可写为
外层的正应力改变了符号但未出现 反向屈服 3.当再次施加的正向弯矩值不 超过M*时，梁将呈弹性响应。
+
s
M* s Me +
+
-
+
-
=
-
s
M* s Me 图 4
4.如卸载到零以后再施加反向弯矩，则开始时的 响应仍是弹性的，当△M满足 M s +( ) s = - s 或 M = -2Me Me 外层纤维开始反向屈服,即弯矩的变化范围不大 于2Me时，结构将是安定的。
都不为零，而且 0 > 0
1 0 0hk ( s )( 0 ) s ( 0 ) 2 E 10 10
截面上开始出现屈服状态的条件可由（53）式写为
0 2 1 n , m ( ) 10 3 10
消去 0 后便有
2n 3m 2 (54)
适用：
2 s Ms > M ≥Me 或： K ≥Ke = Eh
*
*
当
K* ≤ Ke 时， 显然有
K0 = 0
3、残余应力
EKyM y 1 (Me *M*) y, 0y*h/ 2, J J 0 * M s y, h/ 2 yh/ 2, J
* 其中K =
2 横向载荷作用下梁的弹塑性分析
一、梁的弹性极限载荷
研究矩形截面的理想弹塑性悬臂梁，在端点受集中力作用 梁的弯矩：
P A B M x Me Ms L x
M(x) = -(L- x)P
当P增至
2
（ 19 ）
Me bh P = s e = L 6L
根部的弯矩
M = -Me
X=0截面的最外层纤维开始屈服
(8)
教材P155式(5.56)
——弹性极限弯矩
2 s 2s Ke Eh h
(9)
——弹性极限曲率 则（6）式的无量纲形式可写为
M / Me K / Ke
(6' )
三、弹塑性阶段
考虑 M > Me 的情形 设弹塑性区交界处的 y 值 为 ys 有
h 2Biblioteka ssh2h ys 2
s s
y h / 2
0 h / 2
y h/2 y
s
x
s
s
(a)
(b)
(c) 图 12
(d)
分析： 梁中应变为零的纤维称为中性层，中性层的y坐标为
= Ky +0
应力分布：
(1)
y 0
1 oh k 2
(5)
(50)
1.梁处于弹性阶段：
= E = E(Ky +0 )
y ys h /2 M 2b 0 y ( ) s dy ys y s dy ys
2 1 ys 1 2 2 s bh 3 M (3 ) e 12 h/2 2
h 3 2 M / M e ys 3 2 M / Me 2
x 3 2 P (1 x / L)
P e


1 2
(0 x )
(20)
在 x = 0 处， (0) = (3- 2P / P e ) 当 (0) = 0 时，M(0) = -Ms
1 2
3 P= P e =P s 2
与 P s 相应的 值可由
Ps 称为塑性极限载荷
(14)
或
K (signM ) 1 . Ke 3 2 M / Me
对比弹性解
M / Me K / Ke
M / Me
1.5 1
A
B
M/Me=1.48
O
1
2
3
4
图 3
5 K / Ke
1、表明虽然梁截面的外层纤维已进入塑性屈服阶段，但由于其 中间部分仍处于弹性阶段，“平截面”的变形特性限制了外层 纤维塑性变形的大小，因而它们是处于约束塑性变形状态， 梁的曲率完全由中间弹性部分控制。
s
Me M M s 图 2
s
M Ms
EKy, 当 y ys s 当ys y h / 2 当y y h / 2. s s
y ys h /2 截面上的弯矩： M 2b 0 y ( y ) s dy ys y s dy s
5.2 梁的弹塑性弯曲问题
§5.2.1 矩形截面梁的弹塑性纯弯曲
关于梁的两个假定（材料力学） ： ① 平截面假定：梁的横截面在变形之后仍然保持平面。 ② 截面上正应力对变形的影响是主要的，其它应力分量的影 响可以忽略。故应力应变关系可简化为正应力σ 和正应变ε 之间的关系。
一、基本关系
b
M y
h
Mx
2 n 0 , m 10
m 1 n2
(55)
——称为在弯曲和拉伸同时作用下的交互曲线 说明： 它是一种广义应力表示的屈服条件。在对梁、板、壳等 结构进行塑性极限分析时，会经常用到这类屈服条件。
当
1 2
(6' )

( x)
x 图 5
3 时 PP s 2P e L / 3,
x 3 2 P (1 x / L)
P e


(0 x )
1 2
(20)
(x) (3x / L) .
L 区间 0 ≤ x ≤ 中的曲率可由下式给出： 3
利用端条件，得
(6)
h /2 2 M 2bEK 0 y dy EIK
1 3 I bh ——截面的惯性矩 12
说明弯矩和曲率之间有线性关系 代入式（5）
M y,
I
(7)
说明应力分布与y成比例
在梁的最上层和最下层，应力的绝对值最大，故开始屈服 所对应的弯矩和曲率为
2 bh Me s 6
若弯矩完全卸到零，即
M M
0 K 1 M 残余曲率的表达式 Ke Me 3 2M / Me
(17)
卸载后的残余曲率与未卸载时的曲率之比：
M M K / K 1 3 2 , Me Me
0 *
或：
3 Ke 1 Ke 0 * 3 K / K 1 , 2 K 2 K
M / Me
2、 M