价键理论
- 格式:ppt
- 大小:132.00 KB
- 文档页数:5


价键理论自1916年路易斯提出经典的共价键理论以来,共价键理论有了很大的发展。
现代共价键理论有两种,一是价键理论,二是分子轨道理论。
(一)价键理论的基本要点价键理论,又称电子配对法,其基本要点如下:1.具有自旋相反的未成对电子的两个原子相互接近,可以形成稳定的共价键。
如果A、B两个原子各有一个自旋相反的未成对的电子,那么这两个未成对电子可以相互配对形成稳定的共价键,这对电子为A、B两原子所共有(共用)。
如果A、B各有两个或三个未成对的电子,则自旋相反的单电子可两两配对形成双键或叁键。
如果A原子有两个未成对电子,B原子有一个未成对电子,那么一个A原子能与两个B原子结合形成AB2型分子,…。
2.原子中未成对的电子数等于原子所能形成的共价键数目(共价键的饱和性)。
共价键是由成键原子中自旋相反的未成对电子配对形成的。
一个原子的一个电子和另一个原子的一个电子配对以后,不能再和第二个电子配对。
因为这时其中必有两个电子的自旋方向相同而相斥。
也就是说一个原子所能形成共价键的数目是一定的。
原子中未成对的电子数等于原子所能形成的共价键数目,这就是共键价的饱和性。
例如,H原子只有一个未成对电子,它和另一个H原子的未成对电子配对后,就不能再与第二个H原子的电子配对了,……。
3.成键电子的电子云重叠越多,核间电子子云密度就越大,形成的共价键就越牢固(共价健的方向性)。
共价键的生成是由于自旋相反的单电子相互配对,电子云重叠的结果。
因此,当两个原子形成分子时,电子云重叠的程度越大,则两原子间的电子云密度越大,生成的共价键就越牢固,所以,在形成共价键时,电子云总是尽可能达到最大程度的重叠。
因此,在形成共价键时,原子间总是尽可能沿着电子云最大重叠方向成键。
s电子云呈球形对称分布,p、d、f电子云在空间都有一定的伸展方向。
在形成共价键时,除了s 电子云和s电子云可以在任何方向上都能达到最大程度的重叠外,p、d电子云的重叠,只有在一定方向上才能使电子云有最大程度的重叠。

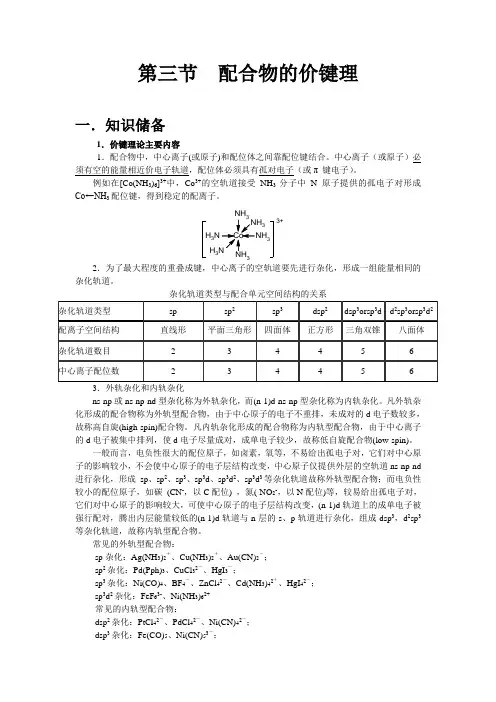


配合物的价键理论可以解释配合物的价键理论是一种重要的理论工具,用来解释物质的晶体结构并解释两个或多个原子间的化学键性质。
它主要关注的是解释原子间分子结构的物理系统诸如电荷分布和能量。
以下列出了价键理论可以用来解释配合物的内容:一、概念:1、原子价键:价键理论主要关注非金属原子之间的化学键,它们由两个原子的电荷之间的作用力形成。
2、亲异性等离子键:在等离子键中,一个原子通过电荷作用另一个原子,形成由两个原子间共享的化学键。
由于这些原子有着不同的化学性质,因此它们也被称为亲异性等离子键。
3、半价键:半价键具有半量电荷,其特征是一个电子被两个原子共同胁迫。
它们连接相同类型原子之间形成不可分割的物质,可以帮助解释某些化学反应方式以及物质结构。
二、连接性:1、化学键:可以根据原子之间的连接能够判断出它们的化学键的性质。
如果原子被强键连接在一起,则它们之间的化学键就会更加牢固,反之也是如此。
2、电荷分布:电荷分布可以解释一种原子价键或者半价键形式的形成原因,当一个原子具有负电荷而另一个具有正电荷时,它们之间就可以存在电荷的失衡。
这种失衡的电荷能促使两个原子形成化学键。
3、分子形状:分子形状是解释半价键性质的重要指标,它表示原子间电荷的分布形状。
如果原子的电荷较为均衡地分布于分子的两部分,就可以形成强的半价键。
三、配位:1、配应力:配应力提供一种有效的方法来理解其间的化学键排列。
如果一种化学物质包含偶合结构,则可以根据其中势能的配应能量和电荷分布来理解它。
2、配位数:配位数是指物质中原子之间结构所能够达到的最大配位数。
具体来讲,如果一种物质包含了六个原子,那么它就能够形成最多6个配位关系。
3、配位角:配位角表示的是原子之间的连接的角度,在配位关系形成之后,它将会保持一定的角度,即配位角。
由于这个角度的影响,它将会影响到其结构的形成。
总之,价键理论可以用来解释配合物的,它解释了物质晶体结构以及原子间的电荷分布和能量、由两个原子间共享的化学键,以及半价键以及其特征、配应力、配位数和配位角等方面。




1、价键理论:以原子轨道作为近似基函数描述分子中电子的运动规律,在阐述共价键本质时,根据Pauli原理的要求,认为一对自旋反平行的电子相互接近时,彼此呈现互相吸引的作用,使体系能量降低,形成化学键。
2、价键理论和分子理论的比较:(1)在数学处理上选用的变分函数不同价键法以原子轨道作为基函数,进行变分法处理,定变分参数;MO(分子理论)法中,每个分子轨道都涉及整个分子,具有离域键概念。
(2)由于选用的基函数不同,所得结果也不相同(3)VB法和MO法在其初级价段都是粗略的近似方法,各有其优缺点,而改进后,两者的结果就彼此接近了。
(4)两者的电子云都在核间密集。
在MO法中,把电子云过多的几种到核间,引起排斥能增大,算得的E偏高,因而求得H2分子的解离能偏低了。
(5)将VB法和MO法推广应用到其他多原子分子:VB法用定域轨道概念描述分子的结构,配合杂化轨道法,适合于处理基态分子的性质;MO法中每个分子轨道都遍及整个分子整体,而分子中各个分子轨道都具有一定的分布和能级,非常适合于描述分子的基态和激发态的性质。
3、价电子对互斥理论:原子周围各个价电子对之间由于相互排斥,在键长一定的条件下,互相间距离愈远愈稳定。
这就要求分布在中心原子周围的价电子对尽可能离得远些,由此说明许多简单分子的几何构型。
4、杂化轨道理论:原子在化合成分子的过程中,根据原子的成键要求,在周围原子影响下,将原有的原子轨道进一步线性组合成新的原子轨道。
这种在一个原子中不同原子轨道的线性组合,称为原子轨道的杂化。
杂化时,轨道的数目不变,轨道在空间的分布方向和分布情况发生改变,能级改变。
组合所得的杂化轨道一般均和其他原子形成较强的键或安排孤对电子,而不会以空的杂化轨道的形式存在。
5、离域分子轨道理论:用分子轨道理论处理多原子分子时,最一般的方法是用非杂化的原子轨道进行线性组合,构成分子轨道,它们是离域化的,即这些分子轨道中的电子并不定域在多原子分子中的两个原子之间,而是在几个原子间离域远动。
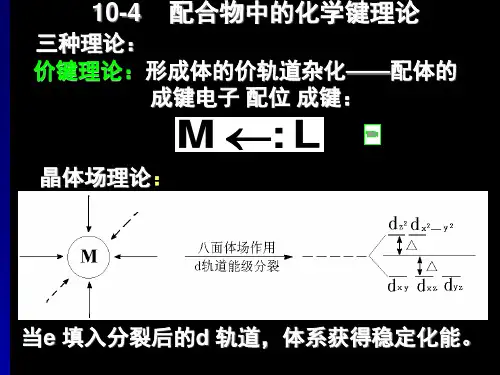
第六章 价键理论价键理论,顾名思义:就是有关分子间化学键的理论。
其核心思想是电子两两配对形成定域的化学键,因而价键理论又称为电子配对理论。
价键理论是在Heitler-London 处理2H 问题的基础上发展起来的。
因此,我们先来回顾一下Heitler-London 方法。
§6.1 Heitler-London 方法在讨论2H 时,H.L 从Pauli 原理出发,即电子轨道自旋波函数必须是反对称的,直接推出了2H 的单态和三态波函数,)()()()())1,31212ab ba ψαββα=± ab ba +:对称的 αββα-:反称 ab ba -:反称 αββα+:对称∴两两组合,只能有+→-⎛⎫⎪-→+⎝⎭a ,b 为归一化的实函数,为氢原子的原子轨道,a 表示在A 核的b 表示在B 核的 |a b S =体系能量(相应于单态和三态):1,31,31,3ˆE Hψψ=∵ˆH不含自旋,∴ψ中自旋可积去,为1,剩下E 只是空间轨道在ˆH 下的作用结果。
∴()1,321ˆ21E ab ba H ab ba S =±±+ ()121ˆ21E ab ba Hab ba S =++⨯+()()21ˆˆˆˆ21ab Hab ab H ba ba H ab ba H ba S =++++ ∵ˆˆab H ab ba H ba =;ˆˆab H ba H ab = ()()21ˆˆ1ab H ab ab H ba S =++ 同理:()()21ˆˆ1ab H ab ab H ba S =-- 写在一起:()()1,321ˆˆ1E ab H ab ab H ba S =±± 定义ˆQ a b H a b = 库仑作用能ˆK ab Hba = 交换作用能 2H 分子在Hamiltonian 在定核近似下,(只与电子坐标有关)可写为: ()()121ˆˆˆ12Hh h r =++ ∴()1,3211E Q K S=±± 其中 Q ab H ab a h a b h b ab g ab ==++ ∵a ,b 对称(a 为A 核1s ,b 为B 核1s ,A ,B 核一样), ∴ 2Q a h a a b g a b=+()()()()()11122K a b H b a a h b b a b h a Sa b g a b==++ S 2S a h b ab g ab =+∵两归一化在函数内积总是小于等于1,即|1a b s =≤"1"=只有 a b = 时∴在我们这种情况下,21S <作为一种近似我们可以把21S +的2S 省去,则能量表示变为,1,3E Q K =± <0 >0∵0K < (2K S a h b ab g ab =+)这一项积分总很小 ∴13E E <即单态为基态,较稳定,符合事实,另外,我们不能省去K 中的S ,如果省去,则K>0,从而31E E <,就不对了。
第三章配合物的化学键理论内容:研究中心原子和配体之间结合力的本性。
目标:解释性质,如配位数、几何结构、磁学性质、光谱、热力学稳定性、动力学反应性等。
四种理论:①价键理论、②晶体场理论、③分子轨道理论、④角重叠模型第一节价键理论(Valence bond theory)由L.Pauling提出要点:①配体的孤对电子可以进入中心原子的空轨道;②中心原子用于成键的轨道是杂化轨道(用于说明构型)。
一、轨道杂化及对配合物构型的解释能量相差不大的原子轨道可通过线性组合构成相同数目的杂化轨道。
对构型的解释(依据电子云最大重叠原理:杂化轨道极大值应指向配体)指向实例sp3、sd3杂化四面体顶点Ni(CO)4sp2、sd2、dp2、d3杂化三角形顶点[AgCl3]2-dsp2、d2p2 杂化正方形顶点[PtCl4]2-d2sp3杂化八面体顶点[ Fe(CN)6]4-sp杂化直线型[AgCl2]-二、AB n型分子的杂化轨道1、原子轨道的变换性质考虑原子轨道波函数,在AB n分子所属点群的各种对称操作下的变换性质。
类型轨道多项式sp x xp p y yp z zd xy xyd xz xzd d yz yzd x2-y2x2-y2d z22z2-x2-y2(简记为z2)轨道波函数是与轨道符号下标多项式按相同的方式变换的。
*在注意到特征标表右边某列中轨道的多项式标记后,即可确定轨道的变换性质。
*s轨道总是按全对称表示变换的。
例:[HgI3]- (D3h群)平面三角形A1′:d z2、sE′:(p x、p y )、(d x2-y2、d xy)A2″:p zE″:(d xz、d yz)2、σ轨道杂化方案(如何确定某一组杂化轨道由哪些原子轨道组成)1)四面体分子AB4(Td)[CoCl4]2-原子A以哪些原子轨道组成在原子A上四个σ轨道的集合,其中每个轨道的瓣指向B原子。
以四个杂化轨道的集合(或四个B原子上指向A 原子的σ轨道的集合)作为分子点群(Td)表示的基,确定该表示的特征标:①不变(1)对杂化轨道波函数的操作有三种情况:②改变符号(-1)③与其他函数变换(0)r1r2r3r4恒等操作,χ(E)=4 C3操作,χ(C3)=1对C2、S4和σd用同样方法处理,得T d E 8C3 3C26S46σdΓ 4 1 0 0 2约化:T d E 8C3 3C2 6S46σdA1 1 1 1 1 1A2 1 1 1 -1 - 1E 2 -1 2 0 0 (z2, x2-y2)T1 3 0 -1 1 -1T2 3 0 -1 -1 1 (xy,xz,yz) (x,y,z)a(A1)=1/24(1×4+8×1×1+3×1×0+6×1×0+6×1×2)=1a(A2)=1/24 [1×4+8×1×1+3×1×0+6×(-1)×0+6×(-1)×2]=0a(E)= 1/24 [2×4+8×(-1)×1+3×2×0+6×0×0+6×0×2]=0 a(T1)=1/24 [3×4+8×0×1+3×(-1)×0+6×1×0+6×(-1)×2]=0a(T2)=1/24[3×4+8×0×1+3×(-1)×0+6×(-1)×0+6×1×2]=1约化结果Γ=A1+T2这说明组成杂化轨道的四个原子轨道中,必有一个是属于A1表示的原子轨道,另三个为属于T2表示的三个原子轨道。