当前位置：文档之家 › 稳态误差的计算_图文(精)

稳态误差的计算_图文(精)

  • 格式：ppt
  • 大小：740.50 KB
  • 文档页数：47

下载文档原格式

  / 47

合集下载

3-6线性系统的稳态误差计算ppt2010

3-6线性系统的稳态误差计算ppt2010

典型输入下的稳态误差与 静态误差系数(P110-111) r(t)=R· 1(t) R(s)=R/s R(s) E(s) C(s) G(s)H(s) R ess= kp 1+ lim k s→0 sν 1 E(s)=R(s) r(t)=V· R(s)=V/s2 t 1+G(s)H(s) V ess= kv k 若系统稳定, lim s· ν s s→0 则可用终值定理求ess r(t)=At2/2 R(s)=A/s3 R(s) ess= lim s A s→0 k GH 1+ ν 0 0 ess= s 2· k ka lim s ν s s→0
封面
3-6目录
1.误差与稳态误差 2.系统类型 3.阶跃输入作用下的稳态误差与静态位置误差 系数 4.斜坡输入作用下的稳态误差与静态速度误差 系数 5.加速度输入作用下的稳态误差与静态加速度 误差系数 6.扰动作用下的稳态误差 7.减小或消除稳态误差的措施
误差定义(P107-109)
R(s) E(s)
不同的型别(表3-6)
稳态误差
静态误差系数
R· 1(t) V· t At2/2
R· 1(t)
R
0型
V· t
At2/2
kp
kv
ka
1+ k
∞
V
∞
k
0
k
0
Ⅰ型
Ⅱ型
0 0
k
∞
A
∞
∞
0
k
0
k
∞
r(t)=At2/2 r(t)=R· 1(t) 小结： A R 1 e与k的关系 s ess= s→0 e2ss= 与ν的关系 k e 1+ lim 表中误差为无穷时系统还稳定吗? 2· k lim s r(t)=V·2 t sν ν s→0 s→0 3 e与r的关系 s (t ) 1(t ) 2t 3t 时如何快速求出 ss ? r e

稳态误差的计算_图文(精)

稳态误差的计算_图文(精)

ess 与输入和开环传递函数有关。 显然， 假设开环传递函数 Gk (s) 的形式如下：
K Gk ( s ) s
2 ( s 1 ) ( s i k 2 k k s 1) 2 ( T s 1 ) ( T s j l 2 lTl s 1) j 1 l 1 i 1 n1 k 1 n2 m1 m2
R(s)
E ' (s) E (s) H (s)
E’(s) 1/H(s)
N(s)
C(s)
e(t)
E(s)
+
B(s)
式中： r(t)为给定输入； 图 典型反馈系统结构图 b(t)为系统主反馈信号。 H （ s ）是测量装置的传递函数（通常我们认为是理想的）， 故此时误差就是给定输入与测量装置的输出量之差。 误差的定义
s 0
当 0时，K v lim sKG0 ( s ) 0 ,
s 0
当 1时，K v lim KG0 ( s ) K , s 0 K 当 2时，K v lim G0 ( s) , s 0 s 结论：
0型系统稳态时不能跟踪斜坡输入
ess 1 ess K ess 0
单位阶跃函数输入时的稳态误差
1 当输入为 R ( s ) 时（单位阶跃函数） s sR(s) 1 1 1 ess lim s 0 1 G ( s) 1 lim Gk (s) 1 lim K G (s) 1 K p k s 0 0 s 0 s 式中：K p lim Gk ( s ) 称为位置误差系数； s 0 1 当 0时，K p lim KG0 ( s ) K , ess s 0 1 K K 当 1时，K p lim G0 ( s ) , ess 0 s 0 s K p 的大小反映了系统在阶跃输入下的稳态精度。 K p 越大，ess 越 小。所以说 K p 反映了系统跟踪阶跃输入的能力。

3-5稳态误差的分析与计算

3-5稳态误差的分析与计算

0型 系统
m
K (TjS 1) G(s) j1
n
(TiS 1)
i 1
抛物线输入 Ⅱ型系统
系统开环传递函数中 不含积分环节
KPlim G(s)K
s0
ess
1 1 K
阶跃输入时，误差系数=K
输出始终不会等于输入，存在稳态误差
Klim SG (s)0 斜坡输入时，误差系数=0
e s 0 ss 稳态误差无穷大（输出不能跟随输入）
三种典型输入下对应于“0”“I”“Ⅱ”型三 种系统
有九种情况，误差的计算公式列表如下：
给定输入
给定稳态误差的终值 0型系统 I型系统 Ⅱ型系统
1(t)
1/(1+K)
0
0
t
∞1/K0源自t2/2∞∞1/K
注意: (1) 尽管将阶跃输入、速度输入及加速度输入下 系统的误差分别称之为位置误差、速度误差和加 速度误差，但对速度误差、加速度误差而言并不 是指输出与输入的速度、加速度不同，而是指输 出与输入之间存在一确定的稳态位置偏差。
i1 n1
(is1) (k2s2 2kks1)
k1 n2
(Tjs1) (Tl2s2 2lls1)
j1
l1
稳态误差系数仅与系统参数K、(积分环节个数—系统 型号)有关，对应＝0、1、2 称 0、I、Ⅱ型系统
0、I、Ⅱ型三种系统 分别三种典型输入 稳态误差有九种情况
阶跃输入 斜坡输入
0型系统 I型系统
3. 稳态误差与系统传递系数有关
4. 稳态误差与扰动有关
本章结束
给定输入下的稳态误差与稳态误差系数
阶跃输入下:
e ssr
1
1 K
P
KPlimG(s) s0

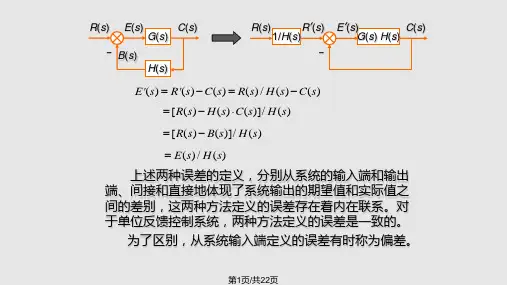
线性系统的稳态误差PPT课件

线性系统的稳态误差PPT课件

N (s)
I型系统：ν=1
1 1, 2 0 1 0, 2 1
➢对参考输入，都是I型系统。 ➢抗扰动的能力却完全不同。
1 1, 2 0
阶跃信号 N(s) R / s 斜坡信号 N (s) R / s2
essn
lim s0
s2K2 s K1K2 K3
R s
0
essn
lim s2K2 s0 s K1K2 K3
所求开环传递函数为
G(s)
s(s2
2 3s
4)
第11页/共22页
五、扰动作用下的稳态误差
扰动不可避免
扰动稳态误差
负载力矩的变化、放大器的零点漂移、电网电压波动 和环境温度的变化等，这些都会引起稳态误差。
扰动稳态误差的大小反映了系统抗干扰能力的强弱。
R(s)
-
E(s) G1(s)
N(s) C(s)
斜坡稳态误差只与G1(s)、H(s)中的增益K1 K3成反比。 至于扰动作用点后的G2(s) ，其增益的大小K2和是否有 积分环节，它们均对减小或消除扰动引起的稳态误差没
有什么作用。
第16页/共22页
II型系统：ν=2
1 2, 2 0
三种可能的组合 1 1, 2 1
1 0, 2 2
➢第一种组合的系统具有II型系统的功能，即对于阶跃和
1]
N
(s)
系统的输出量完全不受扰动的影响 Cn (s) 0
G2 (s)[Gn (s)G1(s) 1] 0
Gn (s)
1 G1 (s)
(对于扰动实现 全补偿的条件)
➢引入前馈后，系统的闭环特征多项式没有发生任何
变化，即不会影响系统的稳定性
➢由于G1(s)分母的s阶次一般比分子的s阶次高，故

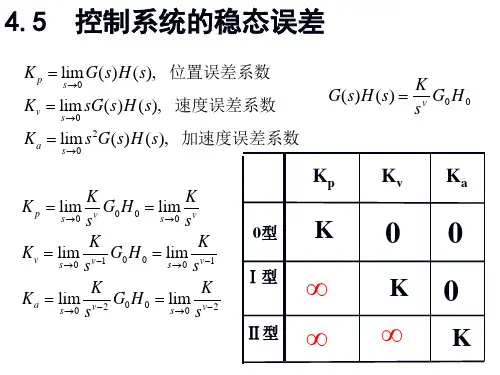
第8讲控制系统的稳态误差ppt课件

第8讲控制系统的稳态误差ppt课件

1 2
1 essa Ka
例：某控制系统的结构图为
r(t) 51(t)
10
C(s)
- s2 2s 1
H (s)
试分别求出H(s)=1和H(s)=0.5时，系统的稳态误 差(定义在输出端)。
解:当H(s)=1时，系统的开环传递函数为
G(s)
s2
10 , k 2s 1
10,
0
则系统稳态误差 当H(s)=0.5时,
G(s)H (s)
K1
P(s) Q(s)
1
Q(s) K1P(s) 0
K1
Q(s) P(s)
由于根轨迹上的分离点与特征方程式的重根相对应，
即满足： D(s) Q(s) K1P(s) 0
D(s) Q(s) K1P(s) 0
利用上两式消去K1，可得
P(s)Q(s) P(s)Q(s) 0 以上分析没有考虑K10(且
2、0＜K1＜0.25 时，两个互异负实根 3、K1=0.25时，s1=s2=－0.5 4、0.25＜K1＜∞时，s1，2=－0.5±0.5j√4k－1
K1
j
K1=0 -1
K1=0.25 K1=0 -0.5 0
K1
所谓根轨迹图，即以系统根轨 迹0→增∞益时K，1为系参统变闭量环，极当点K在1s由平 面上变化的轨迹。
如果实轴上相邻的开环极点、零点之间存在 根轨迹，则或者无分离点，或者存在成对的分 离点。
m
G(s)H (s)
K1
n
(s
i 1
(s
p
zi ) j)
K1
P(s) Q(s)
,
其中P(s)
m
(s zi )，Q(s)
i 1

《自动控制原理》第三章 35 稳态误差计算

《自动控制原理》第三章 35 稳态误差计算

两种定义的联系： E ' ( s ) E ( s ) H (s)
H ( s ) 1时， E ( s ) E ' ( s )
能源与动力学院 第三章 线性系统的时域分析法
3
1. 误差与稳态误差的定义…
e(t ) L1[ E (s)] L1[e (s) R (s)] L1[ R (s) ] 1 G(s)H (s)
3-6 线性系统的稳态误差计算 （Steady-state error）
稳定性 系统性能 动态性能
稳态性能 稳态误差
稳态性能
原理性误差 结构性误差 (附加稳态误差）
系统结构 输入类型、形式 摩擦，间隙 死区等非线性
能源与动力学院
第三章 线性系统的时域分析法
1
3-6 线性系统稳态误差计算
本节内容：
N(s)
C(s)
G2 (s)
H (s)
输出端误差定义
E'n
(s)
Cn(s)
G2(s)
1G1(s)G2(s)H(s)
N(s)
输入端误差定义
En(s)
Cn(s)H(s)
G2(s)H(S) 1G1(s)G2(s)H(s)
ets (t ) ess (t ) 稳态误差
ess ( )
Lim
s0
sE (s)
Lim
s0
1
sR (s) G(s)H
(s)
ess():终值误差 条件s： E(s)在右半平面及析 虚（ 轴原 上点 解除外）
能源与动力学院 第三章 线性系统的时域分析法
4
1. 误差与稳态误差的定义…
例1
R(s) E(S)
误差与稳态误差的定义 系统的类型 输入作用下稳态误差计算 扰动作用下稳态误差 减小或消除稳态误差的措施

稳态误差分析.ppt


sGK
(s)
令：Kv

lim
s0
sGK
(s)
Kv 称为为系统的静态速度误差系数，于是系统在单位斜坡函数作用 下的稳态误差为：
1 ess Kv


0，即0型系统，Kv

lim
s0
sGK
(s)

lim
s0
s

K s
G0 (s) 0 ess

1 Kv




1,
即1型系统，K v
(s)

lim
s0
s2

K s
G0 (s) K
ess

1 Ka

1 K
（4）输入信号为单位阶跃、斜坡、加速度信号时的稳态误差
设输入信号为
r(t) 1 t 1 t 2 2

R(s)

1 s

1 s2

1 s3
利用线性系统的叠加原理，可得系统的稳态误差为
ess
1 1 Kp

1 Kv
lim s0
sE(s)
4．稳态误差分析
设系统开环传递函数如下，并表示为归一化（时间常数）形式
G(s)

b0sm a0sn
b1sm-1 a1sn-1

bm-1s bm an-1s an

K
(1s

1)(
2 2
s2

2
2
2s

1)
s (T1s 1)(T22s2 2T22s 1)

lim
s0
sGK
(s)

稳态误差计算(普通解法)

6.6 稳态误差计算连续系统中计算稳态误差的一般方法和静态误差系数法，在一定的条件下可以推广到离散系统中。

与连续系统不同的是，离散系统的稳态误差只对采样点而言。

6.6.1 一般方法（利用终值定理）设单位反馈的误差采样系统如图6-20所示，系统误差脉冲传递函数为图6-20 离散系统结构图)(11)()()(z G z R z E z e +==Φ )()(11)()()(z R z G z R z z E e +=Φ=如果系统稳定，则可用z 变换的终值定理求出采样瞬时的稳态误差*11(1)()()lim ()lim(1)()lim1()t z z z R z e e t z E z G z →∞→→−∞==−=+ (6-59)式(6-59)表明，线性定常离散系统的稳态误差，与系统本身的结构和参数有关，与输入序列的形式及幅值有关，而且与采样周期的选取也有关。

例6-21 设离散系统如图6-20所示，其中，()1(1)G s s s =+，采样周期，输入连续信号分别为和，试求离散系统的稳态误差。

1s T =)(t r )(1t t 解 系统开环脉冲传递函数[]))(1()1()()(11−−−−−==e z z e z s G Z z G 系统的误差脉冲传递函数368.0736.0)368.0)(1()(11)(2+−−−=+=Φz z z z z G z e闭环极点全部位于平面的单位圆内，可以应用终值定理求稳态误差。

1,20.3680.482z j =±z 当，相应时，)(1)(t t r =)(1)(nT nT r =)1)(−=z z z R ，由式(6-59)求得0368.0736.0)368.0)(1(lim)(21=+−−−=∞→z z z z e z 当，相应时，t t r =)(nT nT r =)(2)1()(−=z z T z R ，于是由式(6-59)求得1368.0736.0)368.0(lim)(21==+−−=∞→T z z z T e z 6.6.2 静态误差系数法由变换算子关系式可知,如果开环传递函数有个的极点，即个积分环节，则与相应的必有个z sTez =)(s G v 0=s v)(s G )(z G v 1=z 的极点。

电气及其自动化专业之静态误差系数与稳态误差计算(共 31张PPT)


知识点三：静态速度误差系数Kv
结论：
（1）Kv的大小反映了系统在斜坡输入下消除误差的 1 Kv越大，稳态误差越小； e ss es K
v
（2）0型系统在稳态时，无法跟踪斜坡输入信号；
（3）I型系统在稳态时，输出与输入速度相等，但有 1 1 的常值位置误差； ess Kv K （4）II型或II型以上系统在稳态时，可完全跟踪斜坡
结论：
（1）Kp的大小反映了系统在阶跃输入下消除误差的 1 Kp越大，稳态误差越小； e ss e ss 1 K p 1 （2）0型系统对阶跃输入引起的稳态误差为常值，大 K越大，稳态误差越小，但总有差，所以把0型系统
（3）在阶跃输入下，若要求系统稳态误差为零，则 或高于I型系统。
问题：如果输入信号不是阶跃信号，那么系统稳态误
后的传递函数无关。
函数的结构及参数有关 ，但与干扰作用
改善系统稳态精度的途径
从上面稳态误差分析可知，采用以下途径来 系统的稳态精度：
＊1. 提高系统的型号或增大系统的开环增益， 定性变差，甚至导致系统不稳定。
＊ 2. 增大误差信号与扰动作用点之间前向通 的稳态误差。但同样也有稳定性问题。 ＊ 3. 采用复合控制，即将反馈控制与扰动信 馈或与给定信号的顺馈相结合。
1 ess R Kv
例2： 已知某单位负反馈系统的开环传递函数为
5 G (s) s(s1 )(s2)
试求系统输入为1(t),10t,3t2时系统的稳态误差。
解题步骤：
（1）判断系统稳定（省略）
例3： 已知两个系统如图(a)(b)所示。输入 试分别计算两个系统的稳态误差。
R () s
第9讲 静态误差系数与 误差计算
知识点一：系统的类型

《自动控制原理》第三章稳态误差计算(共28张PPT)优秀

kp
K
位置误差
ess
R 1 kp
R
1 K
I
0
II
0
III
0
7
第七页，共28页。
3. 输入作用下稳态误差计算…
（2）斜坡作用下的稳态误差
R
r(t)R,tR(s)s 非过主阻导 尼极点>1：响除应主直导接极收点敛外，的系其统他有闭两环个极不点等2的负实根
速度误差不是速度上存在稳态误差 误差与稳态误差的定义
)
1
R Lims R 输入作用下稳态误差计算…
s0
第二十三页，共28页。 LimsG(s)H(s) K Lims 临界稳定：若系统的响应随时间的推移而趋于常值或等幅正弦振荡
开环系统的静态误差s系0数Kp,Kv,Ka；
s0
输入作用下稳态误差计算…
kvL s 0ism G (s)H(s), essk R v
（1）阶跃作用下的稳态误差
r(t)R1(t),R(s)R s
ess
Lim sR(s) s0 1G(s)H(s)
Lims1R(s)
s0
K Lims
s0
1
R LimG(s)H(s)
Lims R
s0
K Lims
s0
s0
kpL s 0iG m (s)H (s), ess1 R kp
系统 型别
0
静态位置 误差系数
18
第十八页，共28页。
19
第十九页，共28页。
主导极点: 如果在所有的闭环极点中，距虚轴
最近的极点周围没有闭环零点，而其他闭环极点 又远离虚轴，那么距虚轴最近的极点在系统响应 过程中起主导作用，这样的闭环极点称为主导极 点 非主导极点：除主导极点外的其他闭环极点
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
如果要求对于阶跃作用下不存在稳态误差，则必须选用Ⅰ型及Ⅰ 型以上的系统。习惯上，阶跃输入作用下的稳态误差称为静差
>> step(feedback(tf(10*[0.0,1],conv([1,0],[1.67,1])),1),0:.01:35)
>> step(feedback(tf(10*[0.0,1],conv([1,1],[1.67,1])),1),0:.01:35) Step Response
K=0.3
阶跃响应
ห้องสมุดไป่ตู้
0
2
4
6
8
10 Time (sec)
12
14
16
18
20
单位加速度函数输入时的稳态误差 1 当输入为R ( s ) 3 时（单位加速度函数） s sR(s) 1 1 1 ess lim 2 s 0 1 G ( s) lim s Gk (s) lim K G (s) K a k s 0 0 s 0 s 2 式中： K a lim s 2Gk ( s ) 称为加速度误差系数；
单位阶跃函数输入时的稳态误差
1 当输入为 R ( s ) 时（单位阶跃函数） s sR(s) 1 1 1 ess lim s 0 1 G ( s) 1 lim Gk (s) 1 lim K G (s) 1 K p k s 0 0 s 0 s 式中：K p lim Gk ( s ) 称为位置误差系数； s 0 1 当 0时，K p lim KG0 ( s ) K , ess s 0 1 K K 当 1时，K p lim G0 ( s ) , ess 0 s 0 s K p 的大小反映了系统在阶跃输入下的稳态精度。 K p 越大，ess 越 小。所以说 K p 反映了系统跟踪阶跃输入的能力。
Time (sec)
从图形中体会误差和稳态误差
单位斜坡函数输入时的稳态误差 1 当输入为R ( s ) 2 时（单位斜坡函数） s sR(s) 1 1 1 ess lim s 0 1 G ( s) lim s Gk (s) lim K G (s) Kv k s 0 0 s 0 s 1 K v lim s Gk ( s ) 称为速度误差系数； 式中：
ess 与输入和开环传递函数有关。 显然， 假设开环传递函数 Gk (s) 的形式如下：
K Gk ( s ) s
2 ( s 1 ) ( s i k 2 k k s 1) 2 ( T s 1 ) ( T s j l 2 lTl s 1) j 1 l 1 i 1 n1 k 1 n2 m1 m2
B(s)
Amplitude
System: untitled2 Final Value: 1
1 0.8 0.6 0.4 0.2 0
r t Cr (t ) 1 t
50 G G1G2 s 1.67s 1
t t
b t C (t )
e t 1 t C (t )
R(s)
E ' (s) E (s) H (s)
E’(s) 1/H(s)
N(s)
C(s)
e(t)
E(s)
+
B(s)
式中： r(t)为给定输入； 图 典型反馈系统结构图 b(t)为系统主反馈信号。 H （ s ）是测量装置的传递函数（通常我们认为是理想的）， 故此时误差就是给定输入与测量装置的输出量之差。 误差的定义
注意：误差、误差响应、稳态分量、瞬态分量、动态误差、稳态误差等概念
从图形和公式中体会误差和稳态误差
2 1.8 1.6 1.4 1.2 Step Response
R(t)
E(s)
N(s)
+
H(s)=1
C(s)
C(t)=b(t)
System: untitled1 Settling Time (sec): 7.54
System: untitled1 Final Value: 0.909 System: untitled4 Final Value: 0.5
G G1G2
1 s 11.67s 1
35
0
>> step(feedback(tf(1*[0.0,1],conv([1,1],[1.67,1])),1),0:.01:35) 5 10 15 20 25 30
讲授技巧及注 表达式推导、图形显示和表格总结相辅相成。 意事项
3-6 控制系统的稳态误差
系统响应的稳态分量(例如t>ts的输出分量）反映了 系统跟踪给定控制信号或希望输出信号的准确度或抑制 扰动信号的恢复能力。通常用稳态误差来衡量。它与系 统本身的结构、参数及外作用的形式有关，也与元件的 不灵敏、零点漂移、老化及各种传动机械的间隙、摩擦 等因素有关。本书只讨论由于系统结构、参数及外作用 等因素所引起的稳态误差，即原理性误差。 给定稳态误差（由给定输入引起的稳态误差） 扰动稳态误差（由扰动输入引起的稳态误差） 给定输入量变化时，要求系统输出量以一定的精度 跟随输入量的变化，因而用给定稳态误差来衡量系统的 稳态性能。给定输入量不变时，需要分析输出量在扰动 作用下所受到的影响，因而用扰动稳态误差来衡量系统 的稳态性能。
K G0 ( s ) s
K Gk ( s ) s
2 ( s 1 ) ( s i k 2 k k s 1) 2 ( T s 1 ) ( T s j l 2 lTl s 1) j 1 l 1 i 1 n1 k 1 n2
一
从图形和公式中体会误差和稳态误差
Step Response
ess lim e(t ) lim[Cr (t ) C (t )] 0.5 0.5
t t
1
r(t)=1(t)
R(t) E(s)
0.8
N(s)
+
H(s)=2
C(s)
C(t)
B(s)
Amplitude
0.6
System: untitled1 Final Value: 0.5
Ⅰ型系统稳态时能跟踪斜坡输入，但存在一个稳态位置误差 Ⅱ型及Ⅱ型以上系统，稳态时能准确跟踪斜坡输入信号，不存 在位置误差
阶跃响应：零稳态误差
Linear Simulation Results 20 18 16 14 12
斜坡响应：稳态误差为常数
指令：t=0:.01:20; u=t; lsim(feedback(tf(5*[0,1],conv([1,0],[1.67,1])),1),u,t)
s 0
当 0,1时，K a lim s (1, 2) KG0 ( s) 0 ,
s 0
当 2时，K a lim KG0 ( s) K , s 0 K 当 3时，K a lim G0 ( s ) , s 0 s K a 反映了系统跟踪抛物线输入的能力。
第三章 线性系统的时域分析法
3-6 线性系统的稳态误差分析 项目 内容
教 学 目 的 理解稳态及稳态误差的概念，掌握其计算方法和
计算结果，进而熟悉减小或消除稳态误差的措施。
教 学 重 点 稳态误差系数定义和典型输入信号作用下的稳态
误差，即表3－5 ；减小或消除稳态误差的措施。
教学难点
广义（动态）误差的概念和广义（动态）误差系 数的计算方法，各种补偿措施。
二、给定输入作用下系统的误差分析
这时，不考虑扰动的影响。 可以写出随动系统的误差 ： 1 1 E ( s) R( s ) R( s ) 1 G1G2 H 1 Gk
R( s )
E (s)
H
G2
G1
sR( s) ess lim e(t ) lim sE ( s) lim t s 0 s 0 1 G ( s ) k
ess lim e(t ) lim[ r (t ) b(t )] 1 1
>> step(feedback(tf(50*[0.0,1],conv([1,0],[1.67,1])),1),0:.01:35)
0 5 10 15 Time (sec) 20 25 30 35
单位反馈情况：
ess 1 ess K ess 0
0型与Ⅰ型系统稳态时不能跟踪加速度输入
Ⅱ型系统稳态时能跟踪加速度输入，但存在一个稳态位置误差 Ⅱ型以上系统，稳态时能准确跟踪加速度输入信号，不存在位 置误差
1.8 1.6 1.4 1.2 System: untitled2 Settling Time (sec): 6.81
G G1G2
10 s 1.67s 1
R(t) E(s)
N(s)
-
G1 ( s)
+ G ( s) 2
C(s)
B(s)
H ( s)
System: untitled2 Final Value: 1
注意：两种误差定义的统一性其关键在于反馈 传递函数H(s)的确定性、可靠性、准确性。
基本公式
ess lim e (t ) lim[r (t ) b (t )]
t t
稳态误差的定义：对于稳定的系统，误差信号 的稳态分量称为系统的稳态误差，以 ess 表示。
一
稳态误差的定义
给定输入时的稳态误差
Amplitude
1 0.8 0.6 0.4 0.2 0
10 G G G System: untitled1 1 2 s 11.67s 1 Settling Time (sec): 2.86
System: untitled4 Settling Time (sec): 2.49
0.4