当前位置：文档之家 › 线性系统的稳态误差计算

线性系统的稳态误差计算

  • 格式：ppt
  • 大小：1.57 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

线性系统的稳态误差(精)

线性系统的稳态误差(精)

3.6线性系统的稳态误差一个稳定的系统在典型外作用下经过一段时间后就会进入稳态，控制系统的稳态精度是其重要的技术指标。

稳态误差必须在允许范围之内，控制系统才有使用价值。

例如，工业加热炉的炉温误差超过限度就会影响产品质量，轧钢机的辊距误差超过限度就轧不出合格的钢材，导弹的跟踪误差若超过允许的限度就不能用于实战，等等。

控制系统的稳态误差是系统控制精度的一种度量，是系统的稳态性能指标。

由于系统自身的结构参数、外作用的类型（控制量或扰动量）以及外作用的形式（阶跃、斜坡或加速度等）不同，控制系统的稳态输出不可能在任意情况下都与输入量（希望的输出）一致，因而会产生原理性稳态误差。

此外，系统中存在的不灵敏区、间隙、零漂等非线性因素也会造成附加的稳态误差。

控制系统设计的任务之一，就是尽量减小系统的稳态误差。

对稳定的系统研究稳态误差才有意义，所以计算稳态误差应以系统稳定为前提。

通常把在阶跃输入作用下没有原理性稳态误差的系统称为无差系统；而把有原理性稳态误差的系统称为有差系统。

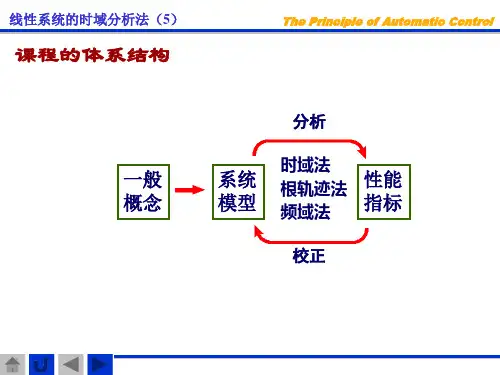
本节主要讨论线性系统原理性稳态误差的计算方法，包括计算稳态误差的一般方法，静态误差系数法和动态误差系数法。

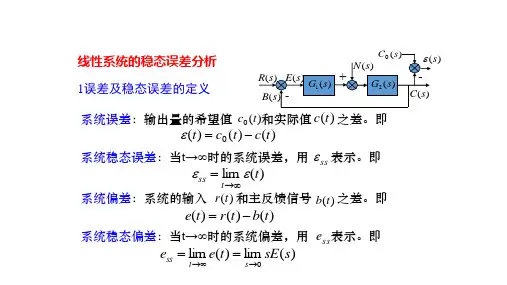
3.6.1 误差与稳态误差控制系统结构图一般可用图3-29（a）的形式表示，经过等效变换可以化成图3-29（b）的形式。

系统的误差通常有两种定义方法：按输入端定义和按输出端定义。

⑴按输入端定义的误差，即把偏差定义为误差，Hsss=（3-25）E-RC)()(s())(⑵按输出端定义的误差5758)()()()(s C s H s R s E -=' （3-26）按输入端定义的误差)(s E （即偏差）通常是可测量的，有一定的物理意义，但其误差的理论含义不十分明显；按输出端定义的误差)(s E '是“希望输出”)(s R '与实际输出)(s C 之差，比较接近误差的理论意义，但它通常不可测量，只有数学意义。

两种误差定义之间存在如下关系：)()()(s H s E s E =' (3-27) 对单位反馈系统而言，上述两种定义是一致的。

稳态误差的计算_图文(精)

稳态误差的计算_图文(精)

ess 与输入和开环传递函数有关。 显然， 假设开环传递函数 Gk (s) 的形式如下：
K Gk ( s ) s
2 ( s 1 ) ( s i k 2 k k s 1) 2 ( T s 1 ) ( T s j l 2 lTl s 1) j 1 l 1 i 1 n1 k 1 n2 m1 m2
R(s)
E ' (s) E (s) H (s)
E’(s) 1/H(s)
N(s)
C(s)
e(t)
E(s)
+
B(s)
式中： r(t)为给定输入； 图 典型反馈系统结构图 b(t)为系统主反馈信号。 H （ s ）是测量装置的传递函数（通常我们认为是理想的）， 故此时误差就是给定输入与测量装置的输出量之差。 误差的定义
s 0
当 0时，K v lim sKG0 ( s ) 0 ,
s 0
当 1时，K v lim KG0 ( s ) K , s 0 K 当 2时，K v lim G0 ( s) , s 0 s 结论：
0型系统稳态时不能跟踪斜坡输入
ess 1 ess K ess 0
单位阶跃函数输入时的稳态误差
1 当输入为 R ( s ) 时（单位阶跃函数） s sR(s) 1 1 1 ess lim s 0 1 G ( s) 1 lim Gk (s) 1 lim K G (s) 1 K p k s 0 0 s 0 s 式中：K p lim Gk ( s ) 称为位置误差系数； s 0 1 当 0时，K p lim KG0 ( s ) K , ess s 0 1 K K 当 1时，K p lim G0 ( s ) , ess 0 s 0 s K p 的大小反映了系统在阶跃输入下的稳态精度。 K p 越大，ess 越 小。所以说 K p 反映了系统跟踪阶跃输入的能力。

3.6稳态误差分析

3.6稳态误差分析





s 0
s 0
s 0
系统的型别ν
ess
开环增益K 输入信号R(s)
线性系统的时域分析法（5）
The Principle of Automatic Control
1.阶跃输入
r (t ) R 1(t )
R lim s
s 0 ν s 0 ν
ess
ess
R 1 K
ν=0
ess
Rv K
0 0
∞
Ra K
0
线性系统的时域分析法（5）
The Principle of Automatic Control
R1 R2 R3 1 2 r (t ) R1 R2t R3t 叠加原理 ess 1 K p Kv Ka 2
例 2：系统结构图如图所示，已知输入r (t ) 2t 4t , 求系统的稳态误差。
称为零型系统 称为I型系统 称为II型系统 的系统不易稳定，也不多见。
当s→0时，G0(s)H0(s)→1
线性系统的时域分析法（5）
The Principle of Automatic Control
ess lim SEs lim sΦ e s Rs lim
s 0 s 0 s 0
系 统 型 别
静态误差系数 阶跃输入 r (t ) R p 1(t ) 斜坡输入r (t ) Rv t 位置误差essp
Kp
Kv
Ka
Rp 1 K p
速度误差 e ssv
Rv Kv
Ra Ka
0 I II III
K ∞ ∞ ∞
0 K ∞ ∞
0 0 K ∞
Rp 1 K

3-6线性系统的稳态误差计算

3-6线性系统的稳态误差计算
i=1 n 1 i k =1 n2 k j =1 j l =1 l
m 1
m2
2
+ 2ζ kτk s +1) + 2ζlTs +1) l
∏(T s +1)∏(Ts
=
2
K ⋅ G0 (s) sν
sR(s) 1 essr = lim = = s→0 1+ G (s) 1+ limGk (s) k
s→0
1 1 = K 1+ Kp 1+ lim ν ⋅ G0 (s) s→0 s
三、扰动作用下的稳态误差(3) 扰动作用下的稳态误差(3) [例]系统结构图如图所示。当 r(t) = n(t) = 1(t) 系统结构图如图所示。 时，求系统的稳态误差 ess；若要求稳态误差 为零，如何改变系统结构。 为零，如何改变系统结构。 解：该系统对给定输入而言属于Ⅰ型系统。 该系统对给定输入而言属于Ⅰ型系统。 所以当给定输入为单位阶跃函数时的稳态误差 essr = 0
3、单位抛物线输入时的稳态误差
R(s) =
1 s3
sR(s) 1 essr = lim = = 2 s→0 1+ G (s) lims ⋅ Gk (s) k
s→0
1 1 = K Ka lim ν −2 ⋅ G0 (s) s→0 s
∞ 1 = K 0
Ka
根据
ν =0,1 ν =2 ν ≥3
m2
=
K ⋅ G0 (s) ν s
K－开环增益
系统型别（即积分环节的个数） ν − 系统型别（即积分环节的个数）
当ν =0，无积分环节，称为0型系统 无积分环节，称为0
当 = ，有一个积分环节，称为Ⅰ型系统 ν 1 有一个积分环节，称为Ⅰ

《自动控制原理》第三第讲

《自动控制原理》第三第讲

误差系数 Kp Kv Ka
单位阶跃 输入
r(t) = u(t)
单位速度 输入
r(t) = t
单位加速 度输入
r(t) = 1 t 2 2
0
K0 0
1 1+K
I
∞ K0
0
II
∞ ∞K
0
∞
∞
1
∞
K
1
0
K
1. 稳态误差与输入信号有关；与开环增益有关；与积分环节的个 数有关。
2. 减小或消除稳态误差的方法： a、增加开环放大系数K； b、提高系统的型号数;
R(s)
E(s) -
G1 ( s)
+ G2 (s) C(s)
H (s) (b)
通常，给定输入作用产生的误差为系统的给定误差
(E=R-HC)，扰动作用产生的误差为扰动误差。认为扰动输入时 系统的理想输出为零，故从输出端的误差信号为：
En
= C理想
− C实际
=
−C实际
=
−Cn
= − G2 1+ G1G2 H
=
lim sv+1R(s)
s→0
lim sv + K
s→0
由上式可见, ess 与系统的型号v﹑开环增益K及输入信号
的形式及大小有关，由于工程实际上的输入信号多为阶跃信号
﹑斜坡信号(即等速度信号) ﹑抛物线信号(即等加速度信号) 或者为这三种信号的组合, 所以下面只讨论这三种信号作用 下的稳态误差问题.
Ka
m
G(s)H (s)
=
K sv
∏ (τ is +1)
i =1
n−v
∏ (Tjs +1)

第六章1(2)线性系统的稳态误差

第六章1(2)线性系统的稳态误差

（2）计算误差方法
（3）适用条件
1）系统稳定 2）按输入端定义误差 3）r(t)作用,且r(t)无其他前馈通道
4.6、线性系统的稳态误差
例4 系统结构图如图所示，当r(t)=t 时，要求ess<0.1，求K的范围。
解 . D(s) s(s 1)(2s 1) K(0.6s 1)
2s3 3s2 (1 0.6K)s K 0
例3 r(t) Asinwt
cs(t)
A sin(wt-arctanwT) 1 w 2T2
cs (t)
1
r(t) 1 w2T2
幅频特性
G( jw) 1 w 2T 2 1
稳态输出幅值 输入量的幅值
幅频特性
cs (t) r(t) arctan wT
G( jw) arctanwT 相频特性
G(s) Uc (s)
1
T CR
1
Ur (s) CRs 1 Ts 1
Uc
(s)
1 Ts
1
s2
Aw w
2
uc (t )
AwT 1 w 2T2
t
eT
A sin(w t-arctanw T) 1 w 2T2
频率响应：线性控制系统在输入正弦信号时， 其稳态输出随频率变化的规律。
6、2 频率特性的概念及几何表示
lim s
s0
A s2
s1s2
K2K3 s1(Ts 1) K1K2K3Ts K1K2K3
A K1
在主反馈口到干扰作用点之间的前向通道中提高增益、设置积分环节， 可以减小或消除干扰作用下产生的稳态误差。
§6. 线性系统的频域分析
§6.2 频率特性的概念及几何表示 §6.3 幅相频率特性曲线（Nyquist图） §6.4 对数频率特性曲线（Bode图） §6.5 频域稳定判据 §6.6 稳定裕度 §6.7 利用开环对数频率特性分析系统的性能 §6.8 利用闭环频率特性分析系统的性能

《自动控制原理》第三章 35 稳态误差计算

《自动控制原理》第三章 35 稳态误差计算

两种定义的联系： E ' ( s ) E ( s ) H (s)
H ( s ) 1时， E ( s ) E ' ( s )
能源与动力学院 第三章 线性系统的时域分析法
3
1. 误差与稳态误差的定义…
e(t ) L1[ E (s)] L1[e (s) R (s)] L1[ R (s) ] 1 G(s)H (s)
3-6 线性系统的稳态误差计算 （Steady-state error）
稳定性 系统性能 动态性能
稳态性能 稳态误差
稳态性能
原理性误差 结构性误差 (附加稳态误差）
系统结构 输入类型、形式 摩擦，间隙 死区等非线性
能源与动力学院
第三章 线性系统的时域分析法
1
3-6 线性系统稳态误差计算
本节内容：
N(s)
C(s)
G2 (s)
H (s)
输出端误差定义
E'n
(s)
Cn(s)
G2(s)
1G1(s)G2(s)H(s)
N(s)
输入端误差定义
En(s)
Cn(s)H(s)
G2(s)H(S) 1G1(s)G2(s)H(s)
ets (t ) ess (t ) 稳态误差
ess ( )
Lim
s0
sE (s)
Lim
s0
1
sR (s) G(s)H
(s)
ess():终值误差 条件s： E(s)在右半平面及析 虚（ 轴原 上点 解除外）
能源与动力学院 第三章 线性系统的时域分析法
4
1. 误差与稳态误差的定义…
例1
R(s) E(S)
误差与稳态误差的定义 系统的类型 输入作用下稳态误差计算 扰动作用下稳态误差 减小或消除稳态误差的措施

线性系统的稳态误差分析

线性系统的稳态误差分析

（阶跃输入） r(t)=1(t)
（斜坡输入） r(t)=t
（加速度输入） r(t)=t2/2
0型系统 1
1 KP
Ⅰ型系统
0 1 Kv
Ⅱ型系统
0
0 1 Ka
• 误差系数Kp、Kv和Ka描述了系统减少或消除稳态误差的能力， 系数值愈大，则给定稳态误差终值愈小。一般来说，在保持瞬态 响应在一个允许的范围内时，希望增加误差系数，如果在静态速 度误差系数和加速度误差系数之间有任何矛盾时，主要考虑前者。
线性系统的稳态误差分析 1误差及稳态误差的定义
C0 (s) (s)
N (s)
R(s) E(s) G1(s) + B(s) -
-
G2 (s) C(s)
系统误差：输出量的希望值 c0 (t)和实际值 c(t) 之差。即
(t) c0 (t) c(t)
系统稳态误差：当t→∞时的系统误差，用 ss 表示。即
ss
lim (t)
t
系统偏差：系统的输入 r(t) 和主反馈信号 b(t) 之差。即
e(t) r(t) b(t)
系统稳态偏差：当t→∞时的系统偏差，用 ess表示。即
ess
lim
t
e(t)
lim
s0
sE(s)
线性系统的时域分析法>>线性系统的稳态误差计算
偏差和误差之间存在一定的关系：
E(s) R(s) B(s) H (s)C0 (s) H (s)C(s) H (s) (s)
ss s0 sG(s)H (s) K lim sG(s)H (s)
v
s0
1 ess Kv
3、输入为单位加速度函数R(s) 1 时
s3
其稳态误差为：

《自动控制原理》第三章-3-5-稳态误差计算

《自动控制原理》第三章-3-5-稳态误差计算

伺服电动机
R(s)
E(s)
1
C(s)
-
s(s 1)
K 1, 1
r(t) 1(t),k p , ess 0
r(t) t, kv 1, ess 1
r(t)
1 2
t2, ka
0, ess
位置随动系统
能源与动力学院 第三章 线性系统的时域分析法
14
4.扰动作用下稳态误差
R(s)
-
E(s)
R(s) E(s) 20
s4
N (s)
+
2
C(s)
s(s 2)
能源与动力学院 第三章 线性系统的时域分析法
28
3-20
R
-
K1
U
K2 S(T1S 1)
C
G(s)
K1K 2
B
s(T1s 1)(T2s 1)
1 T2S 1
(s)
C(s) R(s)
T1T2 s 3
K1K2 (T2s 1) (T1 T2 )s2 s
1
能源与动力学院 第三章 线性系统的时域分析法
7
3.输入作用下稳态误差计算
（1）阶跃作用下的稳态误差
r(t) R 1(t), R(s) R s
ess
Lim sR(s) s0 1 G(s)H (s)
Lim s1R(s)
s0
K Lim s
s0
1
R LimG(s)H (s)
Lim s R
s0
K Lim s
27
参考答案: Kp= ,kv=5,ka=0,essr=0.4，essn=-0.2
四、控制系统如图, r(t) 1 2t, n(t) 1(t), 试计算

3-4 线性系统的稳态误差计算

3-4 线性系统的稳态误差计算

ess 3 lim s
s 0
s(Ts 1) A 3 s(Ts 1) K s
Tips: 系统的稳态误差与系统自身的结构参数、 外作用的类型（控制量，扰动量及其作用点）以 及外作用的形式（阶跃、斜坡或加速度）有关
21:08
2.系统类型



控制系统的稳态误差与开环传递函数的结构和输入信 号的形式密切相关 对于一个给定的稳定系统，当输入信号形式一定时， 系统是否存在稳态误差取决于开环传递函数描述的系 统结构 系统开环传递函数在s平面坐标原点的极点数（开环 传函中串联积分环节的数目）与不同输入信号形式下 系统的稳态误差具有规律性的关系
21:08
依据开环传函中串联积分环节的数目：
B( s) G( s) H (s) R( s)
K ( i s 1) s (T j s 1)
j 1 i 1 n
m
0,0型系统
2, 2型系统
1,1型系统
注意： 尾1形式
3, 使系统稳定相当困难，一般很少采用。
1 K 1 s(Ts 1) s(Ts 1) s(Ts 1) K
e ( s)
E ( s) R( s )
若 r (t ) n(t ) t
s0
e ssr lim s e ( s ) R( s ) lim s
s 0
21:08
s(Ts 1) 1 1 2 s(Ts 1) K s K
若 r (t ) A 1(t )
则
ess1 lim s
s 0
s(Ts 1) A 0 s(Ts 1) K s
s(Ts 1) A A 2 s(Ts 1) K s K

8.3线性离散系统的稳态误差

8.3线性离散系统的稳态误差

T2 0

稳态加速度 误差系数
II型系统： es*s
()

T2 Ka
Ka

lim z
z 1
12
G(z)
8
单位反馈离散系统的稳态误差终值
输入信号
r(t) R0 1(t)
系统型别
r(t) R1t
r(t) R2 t2 2
0型 系统
R0 1 Kp


I型
系统
0
II型 系统
0
R1T
G(
z
)
z 1
0型系统：
es*s
()

1
1 K
p
Kp

lim G( z)
z1
I型系统：
es*s
()

1 1

0
稳态位置 误差系数
II型系统：
es*s
()

1 1

0
6
2 单位斜坡响应的稳态误差终值
es*s
()

lim
z
T
1 G( z)
z 1
0型系统：es*s ()
kT ts
11
[例6-24] 单位负反馈离散系统的开环脉冲传递函数
G(z)

eT (z
z (1 2eT ) 1)(z eT )
采样周期 T 1 s，闭环系统的输入信号为 r(t) 1 t2
2
用稳态误差系数法求稳态误差终值 es*s () ；
用动态误差系数法求 t 20 s时的稳态误差。

T 0


I型系统：
es*s ()

线性系统的稳态误差

线性系统的稳态误差
控制系统的稳态误差是系统控制精度的一种度量，是系统的稳态性能指标。由于系统自 身的结构参数、外作用的类型（控制量或扰动量）以及外作用的形式（阶跃、斜坡或加速度 等）不同，控制系统的稳态输出不可能在任意情况下都与输入量（希望的输出）一致，因而 会产生原理性稳态误差。此外，系统中存在的不灵敏区、间隙、零漂等非线性因素也会造成 附加的稳态误差。控制系统设计的任务之一，就是尽量减小系统的稳态误差。
=
1+
1
K sv
G0
(s)
⑴ 位置输入时， r(t) = A×1(t)
essp
=
lim
s→0
s
Φ
e
(s)
R(s)
= lim s s→0
A1 s 1+ G(s)H (s)
=
A
1+ limG(s)H (s)
s→0
定义静态位置误差系数
Kp
=
lim G(s)H (s)
s→0
=
lim
s→0
K sv
（3-31）
1 s2
=
1 K
图 3-31 控制系统结构图
干扰 n(t) 作用下的误差传递函数为
− Kn
Φ en (s)
=
E(s) N (s)
=
1+
Tn s + 1 K
=
(Tn s
− K n s(Ts + 1)
+ 1)[s(Ts + 1) +
K]
s(Ts + 1)
干扰 n(t) 作用下的稳态误差为
essn
=
lim
=
lim
s→0
K s v−2

第07讲 线性定常系统的稳态误差

第07讲 线性定常系统的稳态误差

第07讲 线性定常系统的稳态
2020/7/28
误差
16
3）静态速度误差系数Kv 当系统的输入为单位斜坡信号时r(t)=t·1(t)，R(s)
1 s2
ess
lim
1
1
s0 1 G(s)H (s) s 2
1 lim sG(s)H (s)
s0
1 K
其差中系K数。lsim0 sG(s)H (s) ，定义为系统静态速度误
误差
9
由拉普拉斯变换的终值定理计算稳态误差，则
ess 代入E(s)表达式得
lim
t
e(t
)
lim
s0
sE
(s)
ess
lim
s0
s
1
1 G(s)H(s)
R(s)
从上式得出两点结论： 1）稳态误差与系统输入信号r(t)的形式有关； 2）稳态误差与系统的结构及参数有关。
第07讲 线性定常系统的稳态
2020/7/28
essr
lim
s0
sEr (s)
lim
s0
s
1
1 G1(s)G2 (s)H (s)
R(s)
第07讲 线性定常系统的稳态
2020/7/28
误差
6
2）扰动信号单独作用下，误差ess (t) b(t)
稳态误差
En (s) B(s) H (s)C(s)
H (s)
G2 (s)
N (s)
1 G1 (s)G2 (s)H (s)
第07讲 线性定常系统的稳态
2020/7/28
误差
17
对于0型系统
K
lim s s0
K (1s 1)( 2s 1)( ms 1)

自动控制原理

自动控制原理

3-6 线性系统的稳态误差计算把在阶跃函数作用下没有原理性稳态误差的系统，称为无差系统；把具有原理性稳态误差的系统称为有差系统。

非线性因素引起的系统稳态误差称为附加稳态误差，或结构性稳态误差。

习惯上常把系统在阶跃输入作用下的稳态误差称为静差。

因而，0型系统可称为有（静）差系统或零阶无差度系统，一型系统可称为一阶无差度系统，二型系统可称为二阶无差度系统。

4-3 广义根轨迹2、附加开环零点的作用增加开环零点也就是增加了闭环零点，闭环零点对系统性能的影响，相当于减小闭环系统的阻尼，从而使系统的过渡过程有出现超调的趋势，并且这种作用将随闭环零点接近坐标原点的强度而加强。

4-4 系统性能的分析1、 闭环零极点与时间响应经验指出，如果闭环零、极点之间的距离比它们本身的模值小一个数量级，则这一对闭环零、极点就构成了偶极子。

在略去偶极子和非主导零、极点的情况下，闭环系统的根轨迹增益常会发生改变，必须注意核算，否则将导致性能的估算错误。

闭环系统零、极点位置对时间响应性能的影响，可以归纳为以下几点：（1） 稳定性。

如果闭环极点全部位于s 左半平面，则系统一定是稳定的，即稳定性只与闭环极点位置有关，而与闭环零点位置无关。

（2） 运动形式。

如果闭环系统无零点，且闭环极点均为实数极点，则时间响应一定是单调的；果闭环极点均为复数极点，则时间响应一般是振荡的。

（3） 超调量。

超调量主要取决于闭环复数主导极点的衰减率1//d σωξ=，并与其他闭环零、极点接近坐标原点的程度有关。

（4） 调节时间。

调节时间主要取决于最靠近虚轴的闭环复数极点的实部绝对值1n σξω= ；如果实数极点距虚轴最近，并且它附近没有实数零点，则调节时间主要取决于该实数极点的模值。

（5） 实数零、极点影响。

零点减小系统阻尼，使峰值时间提前，超调量增大；极点增大系统阻尼，使峰值时间滞后，超调量减小。

它们的作用，随着其本身接近坐标原点的程度而加强。

（6） 偶极子及其处理。

3-5线性系统的稳态误差计算

3-5线性系统的稳态误差计算
er (t ) L1 ER ( s)
en (t ) EN (s) EN ( s) N (s)
1 ER ( s) 1 G1 ( s)G2 ( s) H ( s)
EN ( s)
G2 ( s) H ( s) 1 G1 ( s)G2 ( s) H ( s)
1
ess essr essn 3
（2）r(t ) 1(t ), n(t ) sin 4t，求ess
es (t ) essr
1 s 1 1 1 = lim s s 0 1 1 2 1 s 3 s 1
1 1 3 essn (t ) sin(4t 1800 cos 1 ) 3 5 5
则：essnຫໍສະໝຸດ 1 s N 1 lim s N ( s ) lim N (s) s 0 s 0 K KN N N s
注意：当系统开环传递 函数G1 ( s)G2 ( s) H (s)含有积分环节 (1型及以上系统 )时， 上述计算式成立。
四、改善系统稳态性能的措施
• 增加开环传函Gk(s)的型别：有利于消除ess，增加G1(s)的 型别； • 增加开环传函Gk(s)的增益：有利于减小ess，增加G1(s)的 增益； • 为了减小扰动误差，可以增加偏差点到扰动作用点之间积 分环节个数或放大系数 • 放大系数不能任意放大，积分环节也不能太多（一般2个 ），否则系统将会不稳定。
s0
1 ER ( s) 1 G1 ( s)G2 ( s) H ( s)
essn lim en (t ) lim sEN ( s) lim s EN ( s) N ( s)
t s0 s0
G2 ( s) H ( s) EN ( s) 1 G1 ( s)G2 ( s) H ( s)

西工大、西交大自动控制原理 第六节 线性系统的稳态误差计算11-12

西工大、西交大自动控制原理 第六节 线性系统的稳态误差计算11-12

G2 s Cs
e
s
BERsss
1
1
GH1 ssG2
s
H
s
ef
s
Es F s
1
G2 sH s G1sG2 sH
s
1. 误差与稳态误差
稳态误差的计算
第六节 线性系统的稳态误差计算
Es Er s E f s e sRs ef sF s
1
G1
s
1
G2
s
H
s
Rs
1
G2 sH s G1sG2 sH
；e() R / K
▪ 对Ⅲ型以上系统v 3 ，K a ；e() 0
第六节 线性系统的稳态误差计算
2.用静态误差系数法求稳态误差
系 静态误差 阶跃输入 斜坡输入
统 系数 型 别
R 1t Rt
位置误差 速度误差
K
p
Kv
Ka
ess
R
(1 K p )
ess
R Kv
0K 00 R
1 K
Ⅰ K0 0
2.用静态误差系数法求稳态误差
静态加速度误差系数 K a
定义： Ka
lim
s0
s
2GK
s
lim
s0
s
2Gk
0
s
lim
s0
K sv2
e R R
lim
s0
K s 2
Ka
“加速度误差”
▪ ▪ ▪
对0型系统 对Ⅰ型系统 对Ⅱ型系统
v0
v 1 v2
，，K, KKaaa
0
0 K
；e() ；e()
第六节 线性系统的稳态误差计算

实验四线性定常系统地稳态误差

实验四线性定常系统地稳态误差

实验四 线性定常系统的稳态误差一、实验目的1．通过本实验，理解系统的跟踪误差与其结构、参数与输入信号的形式、幅值大小之间的关系；2．研究系统的开环增益K 对稳态误差的影响。

二、实验原理控制系统的方框图如图4-1所示。

其中G(S)为系统前向通道的传递函数，H(S)为其反馈通道的传递函数。

图4-1 控制系统的方框图由图4-1求得)()()(11)(S R S H S G S E +=（4-1）由上式可知，系统的误差E(S)不仅与其结构和参数有关，而且也与输入信号R(S)的形式和大小有关。

如果系统稳定，且误差的终值存在，则可用下列的终值定理求取系统的稳态误差：)(lim 0S SE e s ss →=（4-2）本实验就是研究系统的稳态误差与上述因素间的关系。

下面叙述0型、I 型、II 型系统对三种不同输入信号所产生的稳态误差ss e 。

1．0型二阶系统设0型二阶系统的方框图如图4-2所示。

根据式（4-2），可以计算出该系统对阶跃和斜坡输入时的稳态误差：图4-2 0型二阶系统的方框图● 单位阶跃输入（sS R 1)(=） 3112)1.01)(2.01()1.01)(2.01(lim 0=⨯+++++⨯=→S S S S S S e S ss （4-3） 输入输出响应曲线如图4-1所示，仿真图如图4-2所示。

图4-3 0型系统阶跃响应稳态误差响应曲线 图4-4 Matlab 仿真曲线由 Matlab 仿真结果来看，输入为单位阶跃信号时，输出稳态误差近似为0.33，符合 4-3式计算的理论值。

● 单位斜坡输入（21)(sS R =） ∞=⨯+++++⨯=→2012)1.01)(2.01()1.01)(2.01(lim SS S S S S e S ss （4-4）输入输出响应曲线如图4-3所示，仿真图如图4-4所示。

图4-5 0型系统斜坡响应稳态误差响应曲线 图4-6 Matlab 仿真曲线由 Matlab 仿真结果来看，输入为单位阶跃信号时，输出稳态误差趋于无穷大，符合4-5式理论计算值。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
函数为
G( s) K S ( S 2 bS C )
p 1 p 2 b C 4 2 p 2 C 2 p K 0.5C K 2 b 3
因为 ess 按定义
1 2 Kr
s 0
Kv
K 0.5, K 0.5C C
令r (t ) Rt 2 / 2，R 常量，R(s) R / s3。
sR(s) sR / s3 R R R ess lim lim lim 2 2 lim 2 s 0 1 G( s) H ( s ) s 0 1 G( s ) H ( s ) s 0 s s G ( s ) H (s ) s 0 s G (s ) H (s ) Ka
系统稳态误差计算通式则可表示为
ess
1 lim s R ( s )
s 0
sR( s) ess lim sE ( s) lim s 0 s 0 1 G ( s ) H ( s )
K lim s
s 0
系统型别 e ss 与 K 开环增益有关 R ( s ) 输入信号
def
E ( s) 1 R(s) 1 H ( s)G( s)
E ( s ) e ( s ) R( s ) R( s ) 1 H ( s)G( s)
e(t ) L1[e (s)R(s)] ets (t ) ess (t )
瞬态分量
稳态分量
E ( s ) e ( s ) R( s )
要求对于阶跃作用下不存 在稳态误差，则必须选用 Ⅰ型及Ⅰ型以上的系统
4.斜坡输入作用下的稳态误差和静态速度误差系数
r (t ) Rt，R 常量，R(s) R / s 2。
sR(s) sR / s 2 R R R ess lim lim lim lim s 0 1 G( s) H ( s) s 0 1 G( s) H ( s) s 0 s sG( s) H ( s) s 0 sG( s) H ( s ) Kv
' e
在s=0的邻域t的邻域
' e
1 '' E(s) e (s)R (s) e (0)R (s) (0)sR (s) e (0)s 2 R (s) 2!
1 '' e ss lim e( t ) e (0)r ( t ) (0)r ' ( t ) e (0)r ' ' ( t ) t 2! 1 1 1 r(t) r' (t) r' ' (t) k0 k1 k2
令K a lim s 2G ( s ) H ( s ) lim
s 0 s 0
K s v2
K a 静态加速度误差系数
Static acceleration error constant
v 0， 1 R ess＝ =const v 2 K 0 v3
0 K a K
分别讨论阶跃、斜坡和加 速度函数的稳态误差情况
3.阶跃输入作用下的稳态误差和静态位置误差系数
r (t ) R 1(t )，R 常量，R(s) R / s。
G( s) H ( s) K K G ( s ) H ( s ) 0 0 s s
ess lim sE (s) 系统在稳态时都不能跟踪加速度输入；
Ⅱ型单位反馈系统，稳态输出的加速度与输入加速度函数相同， 但存在一定的稳态位置误差；
Ⅲ型及Ⅲ型以上的系统，只要系统稳定，其稳态输出能准确跟 踪加速度输入信号，不存在位置误差。
图3-33Ⅱ型单位反馈
系统（的加速度误差）
§3-6线性系统的稳态误差计算
1.误差和稳态误差 2.系统类型
3.阶跃输入作用下的稳态误差和静态位置误差系数
4.斜坡输入作用下的稳态误差和静态位置误差系数 5.加速度输入作用下的稳态误差和静态位置误差系数 6.动态误差系数 7.扰动作用下的稳态误差 8.减小或消除稳态误差的措施
1.误差和稳态误差
系统稳定是前提 控制系统的性能 动态性能 稳态性能 稳态误差 附加稳态误差的计算方法
动态位置 误差系数
动态速度 误差系数
动态加速度 误差系数
动态误差系数的长除法求取
ess 1 1 1 r (t ) r ' (t ) r ' ' (t ) k0 k1 k2
1 1 1 2 s s k 0 k1 k2
e (s)
动态误差系数的简便求法
K 1 b1s b 2 s 2 b m s m G(s)H(s) v s 1 a 1s a 2 s 2 a n v s n v
s 0
s 0
R0 sR(s) s 0 1 G( s) H ( s) 1 K p
令K p lim G ( s) H ( s)
K p : 静态位置误差系数
Static position error constant
K，v 0 可得：K p＝ 0，v 1
R =const，v 0 ess＝1 K 0 v 1
系统的开环增益
1 1 K Kv 200s 1 ess 0.005
例：一单位反馈控制系统，若要求：⑴跟踪单位斜坡输 入时系统的稳态误差为2。⑵设该系统为三阶，其中 一对复数闭环极点为－1＋j和－1－j。。求满足上 述要求的开环传递函数。 解：根据⑴和⑵的要求，可知系统是Ⅰ型三阶系统，因而令其开环传递
K : 系统的开环增益。
0型系统 0 : 为系统中含有的积分环 节数 1 型系统 2 型系统 2时， 型以上的系统，实际上 很难使之稳定，所以这 种类型的 系统在控制工程中一般 不会碰到。 (复合系统)
系统类型(type)与系统的阶数(order)的区别 ！
系统的稳态误差为
1 1 ess max 24 0.04 Kv 600
例：阀控油缸伺服工作台要求定位精度为0.05cm, 该工作台最大移动速度vmax =10cm/s，若系统 为I型，试求系统开环增益。
单位速度输入下的稳态误差为
0.05 e ss 0.005 s 10
令K v lim sG ( s) H ( s) lim
s 0 s 0
K s v 1
K v 静态速度误差系数
Static velocity error constant
v0 R ess＝ =const v 1 K 0 v2
0 K v K
1 r (t ) R0 1(t ) R1t R2t 2 2
R0 R1 R2 ess 1 K p K v Ra
例：I型单位反馈系统的开环增益K=600s-1，系统 最大跟踪速度max =24/s，求系统在最大跟踪 速度下的稳态误差。
1 解：单位速度输入下的稳态误差 ess Kv I型系统 Kv K
ess
本 书 第 8 章 介 绍
稳态误差的不可避免性
摩擦，不灵敏区，零位输出等非线性因素
输入函数的形式不同 (阶跃、斜坡、或加速度)
无差系统： 在阶跃函数作用下没有原理性稳态误差的系统。 有差系统： 在阶跃函数作用下具有原理性稳态误差的系统。
本节主要讨论
系统结构--系统类型 输入作用方式
原理性稳态误差的计算方法
R( s ) 1 H ( s)G( s)
终值定理，求稳态误差。
ess () ess lim sE ( s) lim
s 0
sR( s) s 0 1 H ( s )G ( s )
输入形 式
结构形式
开环传递函数
公式条件：
sE (s)的极点均位于S左半平面（包括坐标原点）
给定的稳定系统，当输入信号形式一定时，系统是否存 在稳态误差，就取决于开环传递函数所描述的系统结构 按照控制系统跟踪不同输入信号的能力来进行系统分类是必要的
K v lim SH ( s )G ( s )
K C
相应闭环传递函数
( s)
K K K S 3 bS 2 CS K (S 2 2S 2)(S p) S 3 ( p 2) S 2 (2 p 2) S 2 p
所求开环传递函数为
G( s)
令G0 (s) H 0 (s) ( i s 1) / (T j s 1)
i 1 j 1
m
n
G( s) H ( s)
K ( i s 1) s (T j s 1) j 1
i 1 n
m
, nm
s 0，G0 (s) H0 (s) 1
G( s) H ( s) K G (s) H 0 (s) 0 s
0型 Ⅰ型 Ⅱ型
ess
类型
输入
r (t ) R0
R0 1 K
r (t ) v0t r (t ) 1 a t 2 0
2
0型 Ⅰ型 Ⅱ型
∞
∞ ∞
0 0
v0 K
0
a0 K
静态误差系数 系统稳态误差 就越小（与 K有关、开环传递函数有 关）
注意:
(1) 尽管将阶跃输入、速度输入及加速度输入下系统的误 差分别称之为位置误差、速度误差和加速度误差，但对速 度误差、加速度误差而言并不是指输出与输入的速度、加 速度不同，而是指输出与输入之间存在一确定的稳态位置 偏差。 (2) 如果输入量非单位量时，其稳态偏差（误差）按比例 增加。 (3) 系统在多个信号共同作用下总的稳态偏差误差等于多 个信号单独作用下的稳态偏差（误差）之和。
4 3.5 3 2.5 2
0.4
n 2