稳态误差计算
- 格式:ppt
- 大小:1.38 MB
- 文档页数:21




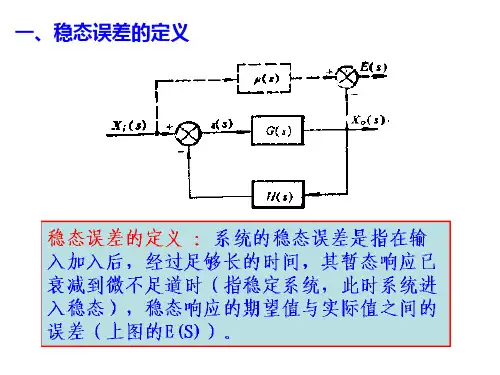






电气及其自动化专业之静态误差系数与稳态误差计算首先,我们需要明确什么是静态误差系数与稳态误差。
静态误差系数是指系统对于稳定输入信号的响应的误差与输入信号的比值。
而稳态误差则是指系统在稳定状态下输出信号与输入信号之间的差异。
对于一个控制系统,如果输入信号为单位阶跃函数(即从0瞬时跃变为1),则系统的静态误差系数为系统的稳态误差。
静态误差系数可以用于评估系统的稳定性和精度,因此在控制系统设计和分析中,静态误差系数的计算是非常重要的任务。
静态误差系数可以分为三个主要类型:零误差系数、恒定误差系数和恒定值误差系数。
零误差系数是指系统对于单位阶跃输入信号的响应是无误差的,即在稳态下,系统的输出完全等于输入信号。
恒定误差系数是指系统的静态误差是一个常数,不受输入信号的幅值大小的影响。
恒定值误差系数是指系统的静态误差与输入信号的幅值大小成线性关系。
计算电气及其自动化专业中的静态误差系数和稳态误差可以通过以下步骤进行:1.建立系统的传递函数模型。
传递函数模型描述了输入与输出之间的关系,是进行稳态误差计算的基础。
2.将传递函数模型转换为控制系统的闭环传递函数模型。
闭环传递函数模型考虑了系统的反馈回路,可以更准确地描述系统的动态响应和稳态误差。
3.根据闭环传递函数模型,计算系统的静态误差系数。
静态误差系数可以通过将输入信号设置为单位阶跃函数,然后计算系统的稳态误差得到。
4.根据系统的静态误差系数,判断系统的稳定性和精确度。
根据系统的静态误差系数,可以判断系统的性能是否满足要求,如果不满足要求,则需要进行控制器的设计和调整。
在实际应用中,静态误差系数和稳态误差计算在控制系统的设计和优化中起着重要的作用。
通过准确计算静态误差系数和稳态误差,可以评估系统的性能和稳定性,并进行控制器的设计和调整,以达到所需的控制精度和稳定性。
总结起来,电气及其自动化专业中的静态误差系数与稳态误差计算是控制系统中一个重要的内容。
通过计算静态误差系数和稳态误差,可以评估系统的性能和稳定性,并进行控制器的设计和调整。