随机信号分析基础第五章习题王永德-答案.

1第一次作业：练习一之1、2、3题1.1 离散随机变量X 由0，1，2，3四个样本组成，相当于四元通信中的四个电平，四个样本的取值概率顺序为1/2，1/4，1/8，和1/8。

求随机变量的数学期望和方差。

解：875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=i i i x X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F求（1）系数A ；（2）X 取值在（0.5，1）内的概率)15.0(<<x P 。

解：⎪⎩⎪⎨⎧<≤-π==其他0201)](2π[cos 2)()(x x A dx x dF x f 由1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P1.3 试确定下列各式是否为连续随机变量的概率分布函数，如果是概率分布函数，求其概率密度。

（1）⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x （2）⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x x x x F （3）0)]()([)(>--=a a x u x u a xx F （4）0)()()(>---=a a x u axa x u a x x F2解：（1）⎪⎩⎪⎨⎧<≥-=-000e 1)(2x x x F x 当0≥x 时，对于12x x ≥，有)()(12x F x F ≥，)(x F 是单调非减函数； 1)(0≤≤x F 成立；)()(x F x F =+也成立。

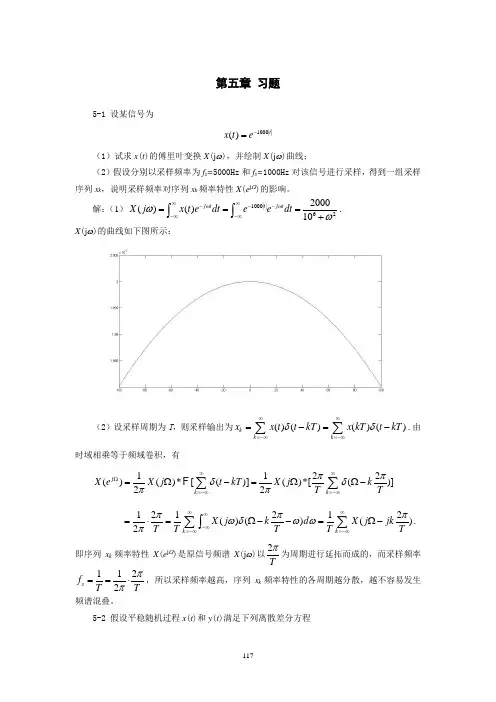
第五章 习题5-1 设某信号为1000||()t x t e -=（1）试求x (t )的傅里叶变换X (j ω)，并绘制X (j ω)曲线；（2）假设分别以采样频率为f s =5000Hz 和f s =1000Hz 对该信号进行采样，得到一组采样序列x k ，说明采样频率对序列x k 频率特性X (e j Ω)的影响。

解：（1）1000||622000()()10j t t j t X j x t e dt e e dt ωωωω∞∞----∞-∞===+⎰⎰. X (j ω)的曲线如下图所示：（2）设采样周期为T ，则采样输出为()()()()k k k x x t t kT x kT t kT δδ∞∞=-∞=-∞=-=-∑∑.由时域相乘等于频域卷积，有1122()()*[()]()*[()]22j k k X e X j t kT X j kT Tππδδππ∞∞Ω=-∞=-∞=Ω-=ΩΩ-∑∑F 121212()()()2k k X j k d X j jk T T T T Tπππωδωωπ∞∞∞-∞=-∞=-∞=⋅=Ω--=Ω-∑∑⎰. 即序列x k 频率特性X (e j Ω)是原信号频谱X (j ω)以2Tπ为周期进行延拓而成的，而采样频率1122s f T Tππ==⋅，所以采样频率越高，序列x k 频率特性的各周期越分散，越不容易发生频谱混叠。

5-2 假设平稳随机过程x (t )和y (t )满足下列离散差分方程11;k k k k k k k x ax e y ay x v ---=-=+式中，|a|<1；e k ，v k ～N (0，σ 2)分布，且二者互不相关。

试求随机序列y k 的功率谱。

解：对1k k k x ax e --=进行离散时间傅里叶变换（DTFT ），且记DTFT(x k )=X (e j Ω)，DTFT(e k )=E (e j Ω)，则有j j j ()(1)()X e ae E e ΩΩΩ--=式中，Ω=ωT s ，称为数字频率（rad ），ω为实际频率（rad/s ），T s 为采样周期（s ）。

第5章习题参考答案1．请在括号内填入适当答案。

在CPU中：(1)保存当前正在执行的指令的寄存器是（IR ）；(2)保存当前正在执行的指令地址的寄存器是（AR ）(3)算术逻辑运算结果通常放在（DR ）和（通用寄存器）。

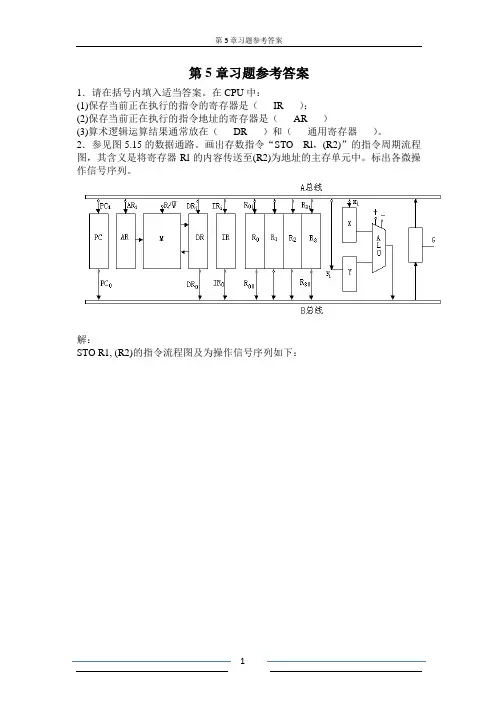
2．参见图5.15的数据通路。

画出存数指令“STO Rl，(R2)”的指令周期流程图，其含义是将寄存器Rl的内容传送至(R2)为地址的主存单元中。

标出各微操作信号序列。

解：STO R1, (R2)的指令流程图及为操作信号序列如下：STO R1, (R2)R/W=RDR O, G, IR iR2O, G, AR iR1O, G, DR iR/W=W3．参见图5.15的数据通路，画出取数指令“LAD (R3)，R0”的指令周期流程图，其含义是将(R3)为地址主存单元的内容取至寄存器R2中，标出各微操作控制信号序列。

解：LAD R3, (R0)的指令流程图及为操作信号序列如下：PC O , G, AR i R/W=R DR O , G, IR iR 3O , G, AR i DR O , G, R 0iR/W=R LAD (R3), R04．假设主脉冲源频率为10MHz ，要求产生5个等间隔的节拍脉冲，试画出时序产生器的逻辑图。

解：5．如果在一个CPU 周期中要产生3个节拍脉冲；T l ＝200ns ，T 2=400ns ，T 3=200ns ，试画出时序产生器逻辑图。

解：取节拍脉冲T l 、T 2、T 3的宽度为时钟周期或者是时钟周期的倍数即可。

所以取时钟源提供的时钟周期为200ns ，即，其频率为5MHz.；由于要输出3个节拍脉冲信号，而T 3的宽度为2个时钟周期，也就是一个节拍电位的时间是4个时钟周期，所以除了C 4外，还需要3个触发器——C l 、C 2、C 3；并令211C C T *=；321C C T *=；313C C T =，由此可画出逻辑电路图如下：6．假设某机器有80条指令，平均每条指令由4条微指令组成，其中有一条取指微指令是所有指令公用的。

1-9 已知随机变量X 的分布函数为20,0(),011,1X x F x kx x x <⎧⎪=≤≤⎨⎪>⎩求：①系数k ； ②X 落在区间(0.3,0.7)内的概率； ③随机变量X 的概率密度。

解：第①问 利用()X F x 右连续的性质 k ＝1第②问{}{}{}()()0.30.70.30.70.70.30.7P X P X F P X F =<<=<≤-=-第③问 201()()0X X xx d F x f x elsedx ≤<⎧==⎨⎩1-10已知随机变量X 的概率密度为()()xX f x kex -=-∞<<+∞（拉普拉斯分布），求：①系数k ②X 落在区间(0,1)内的概率 ③随机变量X 的分布函数 解： 第①问 ()112f xd x k ∞-∞==⎰ 第②问{}()()()211221x x P x X x F x F xfx d x<≤=-=⎰ 随机变量X 落在区间12(,]x x 的概率12{}P x X x <≤就是曲线()y f x =下的曲边梯形的面积。

{}{}()()1010101112P X P X f x dxe -<<=<≤==-⎰第③问()102102xx e x f x e x -⎧≤⎪⎪=⎨⎪>⎪⎩()00()110022111010222xx xxx x x x F x f x dxe dx x ex e dx e dxx e x -∞-∞---∞=⎧⎧≤≤⎪⎪⎪⎪==⎨⎨⎪⎪+>->⎪⎪⎩⎩⎰⎰⎰⎰1-11 某繁忙的汽车站，每天有大量的汽车进出。

设每辆汽车在一天内出事故的概率为0.0001，若每天有1000辆汽车进出汽车站，问汽车站出事故的次数不小于2的概率是多少？,(01)p q λ→∞→→∞→−−−−−−−−→−−−−−−−−→−−−−−−−−→n=1n ,p 0,np=n 成立，0不成立-分布二项分布泊松分布高斯分布汽车站出事故的次数不小于2的概率()()P(2)101k P k P k ≥=-=-= 答案0.1P(2)1 1.1k e -≥=-100.1n p ≥≤实际计算中，只需满足，二项分布就趋近于泊松分布()np!k e P X k k λλλ-=＝＝1-12 已知随机变量(,)X Y 的概率密度为(34)0,0(,)0x y XY kex y f x y -+⎧>>⎪=⎨⎪⎩,,其它求：①系数k ？②(,)X Y 的分布函数？③{01,02}P X X <≤<≤？第③问 方法一：联合分布函数(,)XY F x y 性质：若任意四个实数1212,,,a a b b ，满足1212,a a b b ≤≤，则121222111221{,}(,)(,)(,)(,)XY XY XY XY P a X a b Y b F a b F a b F a b F a b <≤<≤=+--{01,02}(1,2)(0,0)(1,0)(0,2)XY XY XY XY P X Y F F F F ⇒<≤<≤=+--方法二：利用(){(,)},XY DP x y D f u v dudv∈∈⎰⎰)(210{01,02},XY P X Y f x y dxdy <≤<≤=⎰⎰1-13 已知随机变量(,)X Y 的概率密度为101,(,)0x y xf x y ⎧<<<=⎨⎩,,其它 ①求条件概率密度(|)X f x y 和(|)Y f y x ？②判断X 和Y 是否独立？给出理由。

5.1 求题图5.1中三个电路的传输函数（不考虑输出负载）。

RRC1C 2C 1C 2C 1R 2R题图5.1解根据电路分析、信号与系统的知识， 第一个图中系统的传输函数 1/1()1/1j C H j R j C j RCωωωω==++ 第二个图中系统地传输函数 ()21112211/1()/11/1/j C j RC H j R j C j R C C j C R j C ωωωωωωω+==++++ 第三个图中系统地传输函数()2222212111221212121122/1/()//1/1/R j C R j C R j R R C H j R j C R j C R R j R R C C R j C R j C ωωωωωωωωω++==++++++5.2若平稳随机信号)(t X 的自相关函数||2)(ττ-+=BeA R X ，其中，A 和B 都是正常数。

又若某系统冲击响应为()()wth t u t te -=。

当)(t X 输入时，求该系统输出的均值。

解： 因为[]()22X EX R A =∞=所以[]E X A A =±=±。

()()()()()20wt A E Y t E h X t d E X t h d A te dt wξξξξξ∞∞∞--∞-∞±⎡⎤=-==±=⎡⎤⎡⎤⎣⎦⎣⎦⎢⎥⎣⎦⎰⎰⎰ 5.35.4 若输入信号00()cos()X t X t ω=++Φ作用于正文图5.2所示RC 电路，其中0X 为[0,1]上均匀分布的随机变量，Φ为[0,2π]上均匀分布的随机变量，并且0X 与Φ彼此独立。

求输出信号Y(t)的功率谱与相关函数。

解：首先我们求系统的频率响应()H j ω。

根据电路分析、信号与系统的知识，/1/11()()()1/1t RCj C H j h t e u t R j C j RCRCωωωω-==↔=++ 然后，计算)(t X 的均值与自相关函数，[]()1/2X m E X t ==[]{}(){}{}0000(,)cos cos X R t t EXt X t τωωτ+=++Φ+++Φ=⎡⎤⎣⎦()01/31/2cos ωτ+可见)(t X 是广义平稳的。

随机信号分析习题一1. 设函数⎩⎨⎧≤>-=-0 ,0 ,1)(x x e x F x ，试证明)(x F 是某个随机变量ξ的分布函数.并求下列概率：)1(<ξP ，)21(≤≤ξP 。

2. 设),(Y X 的联合密度函数为(), 0, 0(,)0 , otherx y XY e x y f x y -+⎧≥≥=⎨⎩, 求{}10,10<<<<Y X P 。

3. 设二维随机变量),(Y X 的联合密度函数为⎥⎦⎤⎢⎣⎡++-=)52(21exp 1),(22y xy x y x f XY π 求:（1）边沿密度)(x f X ,)(y f Y（2)条件概率密度|(|)Y X f y x ，|(|)X Y f x y4. 设离散型随机变量X 的可能取值为{}2,1,0,1-，取每个值的概率都为4/1，又设随机变量3()Y g X X X ==-。

(1）求Y 的可能取值 （2）确定Y 的分布. （3）求][Y E 。

5. 设两个离散随机变量X ，Y 的联合概率密度为:)()(31)1()3(31)1()2(31),(A y A x y x y x y x f XY --+--+--=δδδδδδ试求：（1)X 与Y 不相关时的所有A 值。

（2）X 与Y 统计独立时所有A 值。

6. 二维随机变量（X ，Y )满足:ϕϕsin cos ==Y Xϕ为在[0，2π]上均匀分布的随机变量，讨论X ,Y 的独立性与相关性。

7. 已知随机变量X 的概率密度为)(x f ,求2bX Y =的概率密度)(y f .8. 两个随机变量1X ，2X ,已知其联合概率密度为12(,)f x x ,求12X X +的概率密度？9. 设X 是零均值，单位方差的高斯随机变量，()y g x =如图，求()y g x =的概率密度()Y f y\10. 设随机变量W 和Z 是另两个随机变量X 和Y 的函数222W X Y Z X⎧=+⎨=⎩ 设X ，Y 是相互独立的高斯变量。

随机信号分析习题一,试证明F(x)是某个随机变的分布函数。

并求卜列概率:< 1), P(1 < ^ < 2) o2. 设的联合密度w 数为求 p{o<x<i ，o<y<i}、3. 设二维随机变g(x ，y)的联合密度函数为fxY^ y) = —exp --(A ：2+2xy + 5y 2) 71 2求：(l)边沿密度八0), f Y (y)(2)条件概率密度人|x (y|x)，A,r (x|y)4. 设离散型随机变的可能取值为1，0，1，，取每个值的概率都为1/4,又设随机变(1) 求r 的可能取值 (2) 确定Y 的分布。

(3)E[Y] o5. 设两个离散随机变量y 的联合概率密度为：fxY J )=2)^(y-l)+|^(x-3)5()’-l) + |<y (x-A)6(y-A)试求：(1) X 与y 不相关吋的所有A 值。

(2)x 与y 统计独立时所有A 值。

6. 二维随机变量(x, y)满足：X =cos (p Y = sin (p识为在[(),上均匀分布的随机变量，讨论X, r 的独立性与相关性。

7. 已知随机变fix 的概率密度为/(X)，求y=/?X 2的概率密度/(y)。

fxY (^y) =，x>0, y>0 ,other8.两个随机变量12，己知其联合概率密度为/(久七)，求1 + 的概率密度？9.设X足零均值，单位方差的高斯随机变量，：v = 如图，求y二以X)的概率密度人(夕)10.设随机变sw和z是w两个随机变s x和r的函数fw = x2 +r2 [z = x2设x，y是相互独立的高斯变景。

求随机变景w和z的联合概率密度函数。

11.设随# L变量w和z是另两个随# L变量x和r的函数J W = X + Y^z = 2(x+ r)己知，求联合概率密度函数人“耿幻。

12.设随机变量X为均匀分布，其概率密度厶=0, 其它(1)求X的特征函数，外(幼。

《随机信号分析》练习题一、 概念题1．叙述随机试验的三个条件。

2．写出事件A 的概率P(A)所满足的三个条件。

3．何谓古典概型？其概率是如何计算的？ 4．两个事件独立的充要条件。

5．两个随机变量独立的充要条件。

6．两个随机过程的独立是如何定义的？7．随机变量X 服从正态分布，写出其概率密度函数表达式，并说明其中各个参数的意义。

8．简述一维随机变量分布函数F （x ）的性质。

9．已知连续型随机变量X 的分布特性，分别用分布函数)(x F X 和概率密度函数)(x f X 表示概率}{21x X x P ≤<。

10． 随机变量X 的特征函数)(μX C 是如何定义的？写出由)(μX C 计算k阶矩)(k X E 的公式。

11．设X 1,X 2,…,Xn 为相互独立的随机变量，其特征函数分别为C 1(μ),C 2(μ),…,Cn(μ)，设∑==n i i X Y 1，则C Y (μ)=？12． 对于一般的复随机变量，其数学期望、方差、协方差各是实数还是复数？13． 写出随机过程X(t)的n 维分布函数定义式。

14． 简述随机过程宽平稳性与严平稳性的区别。

15． 平稳过程与各态历经过程有何关系？16． 设平稳随机过程X(t)的自相关函数为R X (τ)，X(t)依均方意义连续的条件是？17． 已知平稳随机过程X(t)、Y(t)的相关时间分别为X τ和Y τ，若X τ>Y τ，说明X(t) 与Y(t)的起伏程度那个较大？18． 两个随机过程广义联合平稳的条件是什么？19． 平稳随机过程)(t X 的功率谱密度)(ωX G 的物理意义是什么？)(ωX G 与物理谱密度有何关系？20． 白噪声的功率谱密度和自相关函数有何特点？ 21． 简述维纳-辛钦定理并写出其表达式。

22． 何为线性系统？23． 写出希尔伯特变换器的频率响应、幅频响应和相频响应表达式。

24． 写出窄带过程的准正弦表达式和莱斯表达式。

5.5 离散信号()f n 的波形如习题图5-3所示，试画出下列信号的波形。

(2)(1)(4)(2)(6)(1)(1)(8)(1)()(10)(1)(1)f n f n f n f n f n U n f n U n - +×- -- ---+习题图5-3(2)(1)f n -(4)(2)f n32211()10(2)102100n n n f n n f n n n =-ìï =- 3 =-ìïïï= = Þ = =ííïï = îïï î其他其他+×-(6)(1)(1)f n f n--(8)(1)()f n U n---+f n U n(10)(1)(1)5.17 求下列差分方程所描述的系统的单位样值响应。

1(1)()(2)()9y n y n f n --=解：单位样值响应是指当激励信号为()n d 时系统的零状态响应。

要求单位样值响应，输入()()f n n d =，代入差分方程得：1()(2)()(1)9h n h n n d --= LLL在0n >时，()0n d =，有1()(2)09h n h n --= 特征方程为：2121110,933l l l -= Þ =- =1211()()((2)33n nh n C C \ =-+ LLL0()0(())n h n h n < = Q 时，；因为单位样值响应是零状态响应1()(2)()91(0)(2)(0)191(1)(1)(1)09h n h n n h h h h d d d =-+ \ = -+== -+=由(1)式得： 121122(0)(1)1(0)12111(1)(0332h h h C C C h C C C ì =+==üïïïÞ ýí = -+=ïï=þïî将、代入（2）式得：1111()[((]()2323n nh n U n \ =-+5.18 求习题图5-5所示系统的单位样值响应。

第一次作业：练习一之1、2、3题1.1离散随机变量X 由0，1，2，3四个样本组成，相当于四元通信中的四个电平，四个样本的取值概率顺序为1/2，1/4，1/8，和1/8。

求随机变量的数学期望和方差。

解：875.087813812411210)(][41==⨯+⨯+⨯+⨯===∑=ii ix X P x X E81)873(81)872(41)871(21)870(])[(][2224122⨯-+⨯-+⨯-+⨯-=-=∑=i i i P X E x X D109.16471==1.2 设连续随机变量X 的概率分布函数为⎪⎩⎪⎨⎧≥<≤-+<=21201)](2πΑsin[0.500)(x x x x x F 求（1）系数A ；（2）X 取值在（0.5，1）内的概率)15.0(<<x P 。

解：⎪⎩⎪⎨⎧<≤-π==其他201)](2π[cos 2)()(x x A dx x dF x f由 1)(=⎰∞∞-dx x f得 2A 021)](2πAsin[1)]d (2π[cos 2=-=-π⎰∞∞-x x x A21A =35.042)]15.0(2[sin 21)]11(2[sin 21)5.0(F )1(F )15.0(==-π--π=-=<<x P 1.3试确定下列各式是否为连续随机变量的概率分布函数，如果是概率分布函数，求其概率密度。

（1）⎪⎩⎪⎨⎧<≥-=-000e1)(2x x x F x （2）⎪⎩⎪⎨⎧≥<≤<=1110Α00)(2x x xx x F（3）0)]()([)(>--=a a x u x u ax x F （4）0)()()(>---=a a x u ax a x u a x x F解：（1）⎪⎩⎪⎨⎧<≥-=-00e1)(2x x x F x当0≥x 时，对于12x x ≥，有)()(12x F x F ≥，)(x F 是单调非减函数；1)(0≤≤x F 成立； )()(x F x F =+也成立。

第五章习题参考答案与提示第五章数理统计初步习题参考答案与提示.在总体中随机抽取一长度为地样本，求样本均值)(落到之间地概率.答案与提示：由于),(σμ，所以{}<<..在总体中随机抽取一长度为地样本，问样本均值与总体均值地差地绝对值大地概率是多少？)(答案与提示：由于(μσ)，所以{}−>．设为来自总体)(λ地一个样本，、分别为样本均值和样本方差.求及.答案与提示：此题旨在考察样本均值地期望、方差以及样本方差地期望与总体期望、总体方差地关系，显然应由定理来解决这一问题.λλ.．设是来自正态总体地随机样本，.试确定、使统计量，，，)(，)()(−−服从分布，并指出其自由度.χ答案与提示：依题意，要使统计量服从分布，则必需使及服从标准正态分布.解得χ)(−)(−；.．设和独立同分布和分别是来自()，，，，，，，，和地简单抽样，试确定统计量所服从地分布.答案与提示：应用分布地定义，得 ()．设随机变量()(> )，试确定统计量所服从地分布.答案与提示：先由分布地定义知，再利用分布地定义即可.——第五章习题参考答案与提示),(..设总体服从正态分布，而是来自总体)(地简单随机样本，试确定随机变量)( 所服从地分布.答案与提示：由于，)()(χ)()(χ，故)()(．设为来自正态总体地一个样本，),(σμμ已知，求地极大似然估计.σ答案与提示：设为样本地一组观察值.则似然函数为，，，Π−−)()σμσπσμ，（()Σ−−()πσσμ，得地极大似然估计为σΣ−)(ˆμσ.．设),(μ，为来自正态总体地一个样本，试求μ地极大似然估计及矩估计.答案与提示：矩估计法和极大似然估计法是点估计地两种常用方法，所谓矩估计法就是用样本地某种矩作为总体地相应矩地估计，因此需要首先计算（或已知）总体地某（几）种矩，由于本题只涉及一个未知参数，故只要知道总体地某一种矩即可.极大似然估计可依据四个步骤来完成，其关键是正确构造似然函数.μ地极大似然估计为ˆμΣ.μ地矩估计为ˆμΣ.．设为来自正态总体地一个样本，求下述各总体地密度函数中地未知参数地矩估计及极大似然估计.（）⎩⎨⎧<<,)(),(其它θθθ其中−>θ为未知参数.——第五章习题参考答案与提示（）⎪⎩⎪⎨⎧≤>−−,),(λλλ其中λ为未知参数，为常数.>（）⎪⎩⎪⎨⎧>−,)(其它θθ其中,θθ>为未知参数.答案与提示：矩估计法和极大似然估计法是点估计地两种常用方法，所谓矩估计法就是用样本地某种矩作为总体地相应矩地估计，因此需要首先计算（或已知）总体地某（几）种矩，由于本例只涉及一个未知参数，故只要知道总体地某一种矩即可.极大似然估计可依据内容提要中地四个步骤来完成，其关键是正确构造似然函数.（）矩估计：θ−−.极大似然估计：θ−−Σ.（）矩估计：()ˆλ⎡⎤Γ⎢⎥⎣⎦.极大似然估计：Σˆλ.（）矩估计：πθˆ.极大似然估计: Σˆθ．设为总体，，，地一个样本，且服从几何分布，即,)(}{−−，求地极大似然估计量.答案与提示：极大似然估计为．设为总体，，，地一个样本，且服从参数为地二项分布，求地极大似然估计量.答案与提示：地极大似然估计量为.．设为来自总体，，，地一个样本，且μ存在，问统计量（）、——第五章习题参考答案与提示（）是否为μ地无偏估计.（）；−（）()−.答案与提示：依据无偏估计定义，−不是μ地无偏估计；()−是μ地无偏估计. ．设总体服从，为来自总体地一个样本，试问统计量（）、（）、（）是否为),(σμ，，μ地无偏估计，并从无偏估计中找出较好地一个.（）；（）；（）.答案与提示：依据无偏估计定义，统计量（）、（）、（）均为μ地无偏估计.由有效估计定义可判断较好.．设某种元件地使用寿命地概率密度为⎩⎨⎧≤>−−θθθθ，，);()(，其中>θ为未知参数.又设是，，，地一组样本观察值，求θ地极大似然估计值. 答案与提示: 构造似然函数)()(θθ−−ΠΣ−−)(θΣ−−)( θθ(与参数θ无关)由条件，当θ>时， ()()(θ−−θ>)，所以当)(θ时，似然函数取得最大值，从而知.)(ˆθ．设总体地概率分布为θ)(θθ−θθ−其中)(<<θθ是未知参数，利用总体地如下样本值，，，，，，，——第五章习题参考答案与提示，求θ地矩估计值和极大似然估计值.答案与提示：θ地矩估计值为.ˆθ对于给定地样本值，似然函数为，解得)()()(θθθθ−−±θ因>不合题意，所以θ地极大似然估计值为ˆ−θ.．随机地从一批钉子中抽取枚，测得其长度（单位）为，，，，，，，，，，，，，，，，设钉长服从正态分布，试就以下两种情况求总体均值μ地置信度为地置信区间：（）若已知σ；（）若σ未知.答案与提示:() μ地置信度为地置信区间是 (；()，()μ地置信度为地置信区间是.)(，．为了估计灯泡使用时数地均值μ及标准差σ，测试只灯泡，得小时，.如果已知灯泡使用时数服从正态分布，求总体均值μ、标准差σ地置信区间（置信度为）.答案与提示: () μ地置信度为地置信区间是；)(() 地置信度为地置信区间是（）；σσ地置信度为地置信区间是().．随机地取某种炮弹枚做试验，得炮口速度地样本标准差（米秒）.设炮口速度服从正态分布，求这种炮弹炮口速度地标准差σ地地置信区间.答案与提示：σ地置信度地置信区间为().．随机地从批导线中抽取根，从批导线中抽取根，测得电阻()为Ω批导线：，，，，批导线：，，，，，设测定数据分别来自正态总体、，且两样本相互独立.又),(σμ),(σμμ、μ、均为未知，试求σμμ−地置信度为地置信区间.答案与提示: μμ−地地置信区间为（，）.．设两位化验员、独立地对某种聚合物含氯量用同样地方法各作次测定，其测定地样本方差依次为，，设、分别为σσ、——第五章习题参考答案与提示所测定地测定值总体地方差，两总体均服从正态分布.试求方差比地置信度为地置信区间.σσ答案与提示：方差比σσ地置信度为地置信区间是（）.．由经验知某零件重量.技术革新后，抽了六个样品，测得重量为（单位：），，，，，，已知方差不变，问平均重量是否仍为？（)(α）答案与提示：依题意需检验假设μ：，经计算知应接受，即认为平均重量仍是.．原铸造成品率地平均值为，今换用便宜地原料，成品率抽样数据（）如下：，，，，，，，，，，问原料代用后，成品率是否发生了变化？（α）答案与提示：依题意，可认为成品率这样地计量值数据服从正态分布，因此该问题即为方差未知地情况下，检验成品率地平均值是否仍为.检验结果：原料代用后，成品率无显著变化.．设某产品地生产工艺发生了改变，在改变前后分别独立测了若干件产品地某项指标，其结果如下：改变前：，，，，，，；改变后：，，，，，，，.且假定产品地该项指标服从正态分布，求工艺改变前后该产品地此项指标稳定状况有无明显改变（α）？答案与提示：依题意，设工艺改变后地总体为～，工艺改变前地总体为～，从而问题化为检验假设.)(σμ，)(σμ，σ：σ检验结果：认为工艺改变前后该产品地此项指标稳定状况无明显改变.．机床厂某日从两台机器生产地同一零件中，分别抽取若干个样品测量地长度如下第一台机器：，，，，，，，，，，；第一台机器：，，，，，，，，.问这两台机器地加工精度有无显著差异（α）？答案与提示：依题意，可认为样品测量这样地计量值数据服从正态分布，因此比较两台机器地加工精度有无显著差异，即为检验假设σσ成立与否.检验结果：认为两台机器地加工精度无显著差异.．测得两批电子元件地样本地电阻（Ω）为第一批：，，，，，，——第五章习题参考答案与提示第二批：，，，，，.设两批电子元件地电阻分别服从正态总体、，且两样本相互独立.问这两批电子元件地电阻有无显著差异？（),(σμ),(σμα）答案与提示：显然该问题为在方差相等但未知地情况下，对两个正态总体均值是否相等地假设检验既要检验假设. μμμμ≠检验结果：认为两批电子元件电阻均值相等，无显著差异.．假设，，，是来自总体地简单随机样本值.已知服从正态分布),(μ.（）求地数学期望（记为）；（）求μ地置信度为地置信区间；（）利用上述结果求地置信度为地置信区间.答案与提示：（）μ（）由：，，，得：，，，.从而得μ地置信度为地置信区间为()−.（）由上述结果知}{<<−μ即}{<<−μ亦即}{}{<<<<−故地置信度为地置信区间为.)(．设总体服从正态分布),(σμ)(>σ，从总体中抽取简单随机样本，其样本均值为,,,)(>Σ，求统计量)(−Σ地数学期望.解法：考虑)(,),(),(，将其视为取自总体地简单随机样本，则其样本均值、样本方差分别为)(σμΣ)(Σ，()−−Σ−，由于)(σ−，所以.)())((σσ−−解法：记Σ′，Σ′′，显然有′′′.因此——第五章习题参考答案与提示])([−Σ})]()[({′′−′−Σ]})())(()[({′′−′′−′−′−ΣΣ′−])[([[[()] ′′−Σ)()()(σσσ−−−．设随机变量地分布函数为()⎩⎨⎧≤>−，，，αααβαβ),,( 其中参数>>βα.设为来自总体地简单随机样本，求:（）当α时, 求未知参数β地矩估计量；（）当α时,求未知参数β地最大似然估计量；（）当β时, 求未知参数α地最大似然估计量.答案与提示：本题是一个常规题型, 只要注意求连续型总体未知参数地矩估计和最大似然估计都须已知密度函数, 从而先由分布函数求导得密度函数.（）当α时,参数地矩估计量为βˆβ−.（）当α时,求未知参数β地最大似然估计量Σβˆ.（）当β时, 求未知参数α地最大似然估计量，地概率密度为⎪⎩⎪⎨⎧≤>，，，αααβ),(对于总体地样本值, 似然函数为Π⎪⎩⎪⎨⎧>)(,)();()(其他 αααα当时, α越大，越大, 即α地最大似然估计值为)(α>)(α}{ˆα,于是地最大似然估计量为α}{ˆα.——。