随机信号分析基础第三章习题

随机信号分析（第3版）课后习题解答《随机信号分析》课程（32学时）—— 2007年教学内容建议1 概率论基础 1.12 随机信号2.1 两条样本函数为：0)(0=t X 、wt t X cos 21)(1=；1)0,(=x f X 、2)4,(=w x f X π；）（0-)2,(x wx f X δπ= 2.2 3103532)2,(=++=X E 、）（）（）（5-313-312-31)2,(x x x x F X εεε++= 2.3 ）（）（1-2121)21,(x x x F X εε+=、）（）（2-21121)1,(x x x F X εε++=；）（）（）（）（2-,1411,1412-,411,41)1,21,,(21x x x x x x x x x x F X -++-+++=εεεε2.4 略2.5 ）（）（1-1.09.0)5,(x x x F X εε+=；）（）（y x y x y x F ,11.0,9.0)0025.0,0,,(-+=εε；0因为其概率为0.9；1的概率为1（样本函数），它是可预测的，就是样本函数。

2.6 略 2.7 略 2.8 ）（）（121121),(-++=x x n x f X δδ、0121)1(21)(=?+-?=n X E 、{})()]()([)]()()][()([),(2121221121n n n X n X E n m n X n m n X En n Cov X X -==--=δ；不可预测2.9 （2.19）10103523)()(),(2111=?==t t t t Cov σσρ、所以（X,Y ）满足10103;5,2;2,2的高斯分布。

其概率密度函数为：-+--?--?-=-+--?----=5)2(5)2)(2(32)2(5exp215)2(10)2)(2(1010322)2()10/91(21exp 21),(2222y y x x y y x x y x f XY ππ；特征函数为：++-+=)6)(5)(2(21)22(exp ),(21222121v v v v v v j y x XY φ3 平稳性与功率谱密度3.1 kk k u t t u u f-=)4exp(2*21),,;,,(211π ；因为k 阶概率密度函数与绝对时间无关，所以为严格平稳过程。

、随机过程 X(t)=A+cos(t+B)，其中A 是均值为2，方差为1的高斯变量，B 是（0，2π）上均匀分布的随机变量，且A 和B 独立。

求（1）证明X(t)是平稳过程。

（2）X(t)是各态历经过程吗？给出理由。

（3）画出该随机过程的一个样本函数。

（1）（2）3-1 已知平稳过程()X t 的功率谱密度为232()(16)X G ωω=+，求：①该过程的平均功率？ ②ω取值在(4,4)-范围内的平均功率？解[][]()[]2()cos 211,cos 5cos 22X E X t E A E t B A B R t t EA τττ=++=⎡⎤⎣⎦+=+=+与相互独立()()()21521()lim2TT T E X t X t X t X t dt AT-→∞⎡⎤=<∞⇒⎣⎦==⎰是平稳过程()()[]()()4112211222222242'4(1)24()()444(0)41132(1)224414414(2)121tan 13224X X XE X t G d RFG F e R G d d d arc x x ττωωωωωππωωπωωπωπωω∞----∞∞-∞-∞∞--∞∞⎡⎤⨯⎡⎤==⋅=⋅⎢⎥+⎣⎦====+==⎛⎫+ ⎪==⎣⎦=++⎝⎭=⎰⎰⎰⎰⎰P P P P 方法一()方：时域法取值范围为法二-4,4内(频域的平均率法功)2d ω=3-7如图3.10所示，系统的输入()X t 为平稳过程，系统的输出为()()()Y t X t X t T =--。

证明：输出()Y t 的功率谱密度为()2()(1cos )Y X G G T ωωω=-[][]:()[()()]{()()}{()(}2()()()()()()()()2(()[)()(()()]()())Y X X X Y X X Y Y Y X X X Y Y j T j T R E Y t Y t E X t X t T X t X t T R R R R E Y t Y t G F R T T e e G R G R G G G G ωωτττττωτωττωττττωωωω-⇒⇒=+=--+-+-=--=+=-⇔⇔∴=-+-=已知平稳过程的表达式利用定义求利用傅解系统输入输出立叶平变稳换的延时特性2()2()22()(1cos )j T j T X X X e e G G G T ωωωωωω-⎡⎤+-⎢⎥⎣⎦=-3-9 已知平稳过程()X t 和()Y t 相互独立，它们的均值至少有一个为零，功率谱密度分别为216()16X G ωω=+22()16Y G ωωω=+令新的随机过程()()()()()()Z t X t Y t V t X t Y t =+⎧⎨=-⎩ ①证明()X t 和()Y t 联合平稳； ②求()Z t 的功率谱密度()Z G ω？ ③求()X t 和()Y t 的互谱密度()XY G ω？ ④求()X t 和()Z t 的互相关函数()XZ R τ？ ⑤求()V t 和()Z t 的互相关函数()VZ R τ 解:()()4124(1)()()()2[()]()0[()]0()2[()]0()()(,)[()][()]0()()(2)()()()()[()()][()()][()X X X Y XY Z X t Y t R F G e E X t R E X t R eE Y t X t Y t R t t E X t E Y t X t Y t Z t X t Y t R E Z t Z t E X t Y t X t τττωτδττττττ---==∞=⇒=⎡⎤⎣⎦=-⇒=∴+=⋅+=⇒=+=+=++、都平稳＝与与联合独平立稳[][]{}2214||()]()()()()()0()()()16()()()116(3)()0()0(4)()[()()]()()()()()()[()]2(5)(X YX XY Y XY Z X Y Z X Y XY XY XZ X XY X X VZ Y t R R R R R R R R G G G R G R E X t Z t E X t X t Y t R R R F G e R ττττττττττωωωωωτωτττττττωτ--++=+++=∴=++∴=+==+=→==+=+++=+==={}4||)[()()][()()][()()]()()()4X Y E V t Z t E X t Y t X t Y t R R e ττττττδτ-=+=-+++=-=+-3-11 已知可微平稳过程()X t 的自相关函数为2()2exp[]X R ττ=-，其导数为()()Y t X t '=。

第三章，平稳随机过程的n 维概率密度不随时间平移而变化的特性，反映在统计特征上就是其均值不随时间的变化而变化，mx 不是t 的函数。

同样均方值也应是常数。

（2）二维概率密度只与t1,t2的时间间隔有关，而与时间起点t1无关。

因此平稳过程的自相关函数仅是单变量tao 的函数。

则称他们是联合宽平稳的。

第三章Chapter 3 ==========================================3.2 随机过程()t X 为()()ΦωX +=t cos A t 0式中，A 具有瑞利分布，其概率密度为()02222>=-a eaa P a A ，σσ，()πΦ20，在上均匀分布，A Φ与是两个相互独立的随机变量，0ω为常数，试问X(t)是否为平稳过程。

解：由题意可得:()[]()()002121020222220002222=⇒+=*+=⎰⎰⎰⎰∞--∞φφωπσφπσφωX E πσσπd t cos da e a a dad eat cos a t a a ()()()[]()()()()()()[]()()()()()120212021202021202022212020220210120220222020100222222002010212121221122102122121212212122222222222222t t cos t t cos t t cos det t cos da e e a t t cos dea d t t cos t t cos a d ea d t cos t cos da eaadad e at cos a t cos a t t t t R a a a a a a a -=-⨯=-⨯-=-⨯⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫-∞+-=-⨯-=⎩⎨⎧⎭⎬⎫+++---=++=++==-∞∞---∞∞-∞--∞⎰⎰⎰⎰⎰⎰⎰⎰⎰ωσωσωσωωφφωωπσφπφωφωσφσπφωφωX X E σσσσπσπσσπXX ）（，可见()[]t X E 与t 无关，()21t t R ，XX 与t 无关，只与()12t t -有关。

随机信号分析基础作业题第⼀章1、有朋⾃远⽅来，她乘⽕车、轮船、汽车或飞机的概率分别是0.3，0.2，0.1和0.4。

如果她乘⽕车、轮船或者汽车来，迟到的概率分别是0.25，0.4和0.1，但她乘飞机来则不会迟到。

如果她迟到了，问她最可能搭乘的是哪种交通⼯具？解：()0.3P A =()0.2P B =()0.1P C =()0.4P D =E －迟到，由已知可得(|)0.25(|)0.4(|)0.1(|)0P E A P E B P E C P E D ====全概率公式： ()()()()(P E P E AP E B P E C P E D=+++ 贝叶斯公式：()(|)()0.075(|)0.455()()0.165(|)()0.08(|)0.485()0.165(|)()0.01(|)0.06()0.165(|)()(|)0()P EA P E A P A P A E P E P E P E B P B P B E P E P E C P C P C E P E P E D P D P D E P E ?====?===?===?==综上：坐轮船3、设随机变量X 服从瑞利分布，其概率密度函数为2222,0()0,0X x x X x e x f x x σσ-??>=??式中，常数0X σ>，求期望()E X 和⽅差()D X 。

考察：已知()x f x ，如何求()E X 和()D X ？222222()()()[()]()()()()()()()x x E X x f x dxD XE X m X m f x dxD XE X E X E X x f x dx∞-∞∞-∞∞-∞=?=-=-=-?=6、已知随机变量X 与Y ，有1,3,()4,()16,0XYEX EY D X D Y ρ=====，令3,2,U X Y V X Y =+=-试求EU 、EV 、()D U 、()D V 和(,)Cov U V 。

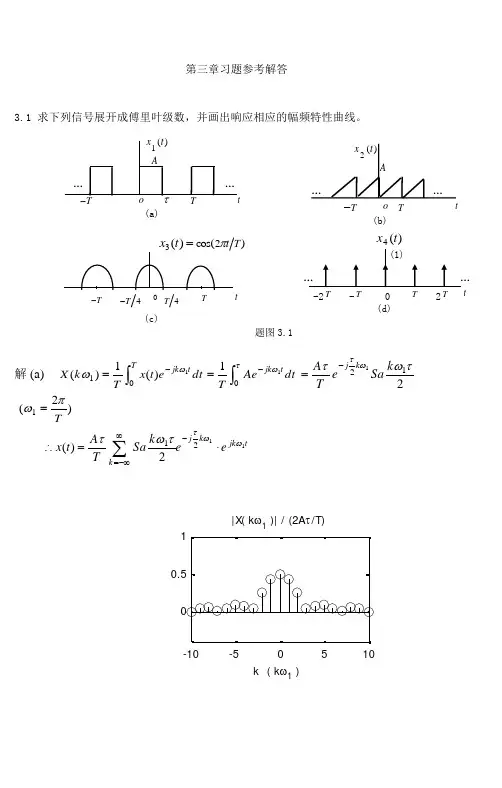
第三章习题参考解答3.1 求下列信号展开成傅里叶级数，并画出响应相应的幅频特性曲线。

解 (a) ⎰-=Ttjk dt et x Tk X 011)(1)(ωω⎰-=τω011dt AeTtjk 2121τωτωτk Sae T A k j -= )2(1Tπω=t jk k j k e e k Sa TA t x 11212)(ωωττωτ⋅=∴-∞-∞=∑3.1解 (b) ⎰-=Tt jk dt e t x Tk X 011)(1)(ωω⎰-=Tt jk dt te T A T011ω⎰--⋅=T t jk e td jk T A 012][11ωω ⎰-+-=T t jk dt e T jk Ak j A 02112ωωπkjA π2= )2(1T πω= ⎰=Tdt t x TX 0)(1)0(2A =∑∞≠-∞=+=∴)0(122)(k k t jk e kjA At x ωπ解 (c) ⎰-=Ttjk dt et x Tk X 011)(1)(ωωdt e TTtjk T T ωπ--⋅=⎰442cos1dt e e Tt k j t k j T T ][21111)1()1(44ωω+---+=⎰][)1(121][)1(1214)1(4)1(14)1(4)1(11111Tk j Tk j Tk j Tk j e ek j T e e k j T ωωωωωω++-----⋅+-⋅+--⋅=2)1sin()1(212)1sin()1(21ππππ--+++=k k k k π2)1(412)1(41-++=k Sa k Sa t jk k e k Sa k Sat x 1)2)1(2)1((41)(ωππ-++=∴∑∞-∞= )2(1T πω=解 (d) ⎰--=221)(1TT t jk n dt e t TF ωδT1=∑∞-∞==∴k tjk eTt x 11)(4ω3.2 求题图3.2所示信号的傅里叶变换。

随机信号分析习题一,试证明F(x)是某个随机变的分布函数。

并求卜列概率:< 1), P(1 < ^ < 2) o2. 设的联合密度w 数为求 p{o<x<i ，o<y<i}、3. 设二维随机变g(x ，y)的联合密度函数为fxY^ y) = —exp --(A ：2+2xy + 5y 2) 71 2求：(l)边沿密度八0), f Y (y)(2)条件概率密度人|x (y|x)，A,r (x|y)4. 设离散型随机变的可能取值为1，0，1，，取每个值的概率都为1/4,又设随机变(1) 求r 的可能取值 (2) 确定Y 的分布。

(3)E[Y] o5. 设两个离散随机变量y 的联合概率密度为：fxY J )=2)^(y-l)+|^(x-3)5()’-l) + |<y (x-A)6(y-A)试求：(1) X 与y 不相关吋的所有A 值。

(2)x 与y 统计独立时所有A 值。

6. 二维随机变量(x, y)满足：X =cos (p Y = sin (p识为在[(),上均匀分布的随机变量，讨论X, r 的独立性与相关性。

7. 已知随机变fix 的概率密度为/(X)，求y=/?X 2的概率密度/(y)。

fxY (^y) =，x>0, y>0 ,other8.两个随机变量12，己知其联合概率密度为/(久七)，求1 + 的概率密度？9.设X足零均值，单位方差的高斯随机变量，：v = 如图，求y二以X)的概率密度人(夕)10.设随机变sw和z是w两个随机变s x和r的函数fw = x2 +r2 [z = x2设x，y是相互独立的高斯变景。

求随机变景w和z的联合概率密度函数。

11.设随# L变量w和z是另两个随# L变量x和r的函数J W = X + Y^z = 2(x+ r)己知，求联合概率密度函数人“耿幻。

12.设随机变量X为均匀分布，其概率密度厶=0, 其它(1)求X的特征函数，外(幼。

《随机信号分析》练习题一、 概念题1．叙述随机试验的三个条件。

2．写出事件A 的概率P(A)所满足的三个条件。

3．何谓古典概型？其概率是如何计算的？ 4．两个事件独立的充要条件。

5．两个随机变量独立的充要条件。

6．两个随机过程的独立是如何定义的？7．随机变量X 服从正态分布，写出其概率密度函数表达式，并说明其中各个参数的意义。

8．简述一维随机变量分布函数F （x ）的性质。

9．已知连续型随机变量X 的分布特性，分别用分布函数)(x F X 和概率密度函数)(x f X 表示概率}{21x X x P ≤<。

10． 随机变量X 的特征函数)(μX C 是如何定义的？写出由)(μX C 计算k阶矩)(k X E 的公式。

11．设X 1,X 2,…,Xn 为相互独立的随机变量，其特征函数分别为C 1(μ),C 2(μ),…,Cn(μ)，设∑==n i i X Y 1，则C Y (μ)=？12． 对于一般的复随机变量，其数学期望、方差、协方差各是实数还是复数？13． 写出随机过程X(t)的n 维分布函数定义式。

14． 简述随机过程宽平稳性与严平稳性的区别。

15． 平稳过程与各态历经过程有何关系？16． 设平稳随机过程X(t)的自相关函数为R X (τ)，X(t)依均方意义连续的条件是？17． 已知平稳随机过程X(t)、Y(t)的相关时间分别为X τ和Y τ，若X τ>Y τ，说明X(t) 与Y(t)的起伏程度那个较大？18． 两个随机过程广义联合平稳的条件是什么？19． 平稳随机过程)(t X 的功率谱密度)(ωX G 的物理意义是什么？)(ωX G 与物理谱密度有何关系？20． 白噪声的功率谱密度和自相关函数有何特点？ 21． 简述维纳-辛钦定理并写出其表达式。

22． 何为线性系统？23． 写出希尔伯特变换器的频率响应、幅频响应和相频响应表达式。

24． 写出窄带过程的准正弦表达式和莱斯表达式。

第三章 习题3-1 设某一随机过程的样本为{x 1，x 2，…，x k }，设k 时刻的样本均值和方差分别为21111(),(1)1kkk ik i k i i x x s x x k k k ====-≠-∑∑和 假定新的观测值为x k+1，试推导样本均值x k+1和样本方差s k+1的更新公式。

解：111k k k kx x x k +++=+. ∵ 121111()k k i k i s x x k +++==-∑，而211()1k k i k i s x x k ==--∑，所以 112211111222111111122112211()()111211 ()()()()11111 0()()(1)(1) k k k k k k k i i k i i k k k k k k k k k i k i k k i i i k k k k kkx x x x s x x x k k k k x x x x kx x x x x x x k k k k k k k k k s x x x x k k k +++++==++++===+++-=-=--++--+=---++-+++-=-+-+-++∑∑∑∑∑2111 ().1k k k k s x x k k +-=+-+∴ 更新公式为11111k k k k x x x k k ++=+++, 21111()1k k k k k s s x x k k ++-=+-+.3-2 设某一随机过程样本由x k =a+bk+v k 描述，其中，v k ～N （0，σ2）；a 和b 是待定的未知参数。

试求估计量a ˆ，b ˆ的CR 下界。

解：未知参数向量为θ=[a ，b ]T 。

首先计算Fisher 信息矩阵，即222222ln (|)ln (|)[][]()ln (|)ln (|)[][]p x p x E E a a b p x p x E E b a b ⎡⎤∂∂--⎢⎥∂∂∂⎢⎥=⎢⎥∂∂⎢⎥--⎢⎥∂∂∂⎣⎦θθI θθθ （3.1.31） 依题意，似然函数可写成22/22111(|)exp[()](2π)2NkN k p x xa bk σσ==---∑θ对上式等号两边取自然对数，并分别对A 和B 求偏导，得到21ln (|)1()Nkk p x xa bk a σ=∂=--∂∑θ21ln (|)1()Nkk p x xa bk kb σ=∂=--∂∑θ容易验证，以上二式的数学期望为零，满足正则条件（3.1.25）。

随机信号分析基础课后练习题含答案第一部分随机变量和概率分布练习题1设离散随机变量X的概率分布函数为：X0 1 2 3 4P X0.05 0.15 0.35 0.30 0.15求E(X)和D(X)。

答案1根据概率分布函数的公式有：$$E(X)=\\sum_{i=1}^n x_i P_X(x_i) = 0 \\times 0.05 + 1\\times 0.15 + 2 \\times 0.35 + 3 \\times 0.30 + 4 \\times 0.15 = 2.25$$$$D(X)=\\sum_{i=1}^n (x_i-E(X))^2P_X(x_i) = 0.710625$$ 练习题2已知随机变量X的概率密度函数为：$$f_X(x) = \\begin{cases} \\frac{1}{3}e^{-\\frac{x}{3}} & x \\geq 0 \\\\ 0 & x < 0 \\end{cases}$$求E(X)和D(X)。

答案2根据概率分布函数的公式有：$$E(X)=\\int_{-\\infty}^{+\\infty}xf_X(x)dx =\\int_{0}^{+\\infty}x\\frac{1}{3}e^{-\\frac{x}{3}}dx=3$$ $$D(X)=E(X^2)-(E(X))^2=\\int_{-\\infty}^{+\\infty}x^2f_X(x)dx-(E(X))^2=\\int_{0}^{+\\infty}x^2\\frac{1}{3}e^{-\\frac{x}{3}}dx-9=\\frac{27}{4}$$第二部分随机过程练习题3设二阶矩有限的离散时间随机过程X n的均值序列为m n，自相关函数为R n(i,j)=E(X i−m i)(X j−m j)，其中 $0 \\leq i,j \\leq N$。

若m n=n2,R n(i,j)=ij(i+j)，求 $E(\\sum_{n=0}^N X_n)$。

3.1 随机电压信号()U t 在各不同时刻上是统计独立的，而且，一阶概率密度函数是高斯的、均值为0，方差为2，试求：（1）密度函数();f u t 、()1212,;,f u u t t 和()1212,,...,;,,...,k k f u u u t t t ，k 为任意整数；（2）()U t 的平稳性。

3.1解：(1)2(;)}4x f u t =-22121,2121,12,21(;,)()()exp{}44u u f u u t t f u t f u t π+==-211,212,1(,,;,,)()}4kiki k k i i i uf u u u t t t f u t ====-∑∏(2)由于任意k 阶概率密度函数与t 无关，因此它是严平稳的。

3.23.33.4 已知随机信号()X t 和()Y t 相互独立且各自平稳，证明新的随机信号()()()Z t X t Y t =也是平稳的。

3.4解：()X t 与()Y t 各自平稳，设X m =[()]E X t ，Y m =[()]E Y t ，()[X()X()]X R E t t ττ=+，()[Y()Y()]Y R E t t ττ=+Z ()[Z()][()Y()][()][()]X Y m t E t E X t t E X t E Y t m m ===⨯=，为常数(,)[Z()Z()][()Y()()Y()][X()()][Y()()]()()()Z X Y Z R t t E t t E X t t X t t E t X t E t Y t R R R τττττττττ+=+=++=+⨯+=⨯=∴()Z R τ仅与τ有关，故Z()t =()Y()X t t 也是平稳过程。

3.5 随机信号()()010sin X t t ω=+Θ，0ω为确定常数，Θ在[],ππ-上均匀分布的随机变量。

若()X t 通过平方律器件，得到2()()Y t X t =，试求：（1）()Y t 的均值； （2）()Y t 的相关函数；（3）()Y t 的广义平稳性。