运动量曲线预计图(直角坐标)

必修二知识点第一章曲线运动（一）曲线运动的位移研究物体的运动时，坐标系的选取十分重要.在这里选择平面直角坐标系．以抛出点为坐标原点，以抛出时物体的初速度v0方向为x轴的正方向，以竖直方向向下为y轴的正方向，如下图所示．当物体运动到A点时，它相对于抛出点O的位移是OA，用l表示.由于这类问题中位移矢量的方向在不断变化，运算起来很不方便，因此要尽量用它在坐标轴方向的分矢量来表示它.由于两个分矢量的方向是确定的，所以只用A点的坐标(x A、y A)就能表示它，于是使问题简化.（二）曲线运动的速度1、曲线运动速度方向：做曲线运动的物体，在某点的速度方向，沿曲线在这一点的切线方向．2．对曲线运动速度方向的理解如图所示，AB割线的长度跟质点由A运动到B的时间之比，即＝，等于AB过程中平均速度的大小，其平均速度的方向由A指向B.当B非常非常接近A时，AB割线变成了过A点的切线，同时Δt变为极短的时间，故AB间的平均速度近似等于A点的瞬时速度，因此质点在A点的瞬时速度方向与过A点的切线方向一致．（三）曲线运动的特点1、曲线运动是变速运动：做曲线运动的物体速度方向时刻在发生变化，所以曲线运动是变速运动．（曲线运动是变速运动，但变速运动不一定是曲线运动）2、做曲线运动的物体一定具有加速度曲线运动中速度的方向(轨迹上各点的切线方向)时刻在发生变化，即物体的运动状态时刻在发生变化，而力是改变物体运动状态的原因，因此，做曲线运动的物体所受合力一定不为零，也就一定具有加速度．（说明：曲线运动是变速运动，只是说明物体具有加速度，但加速度不一定是变化的，例如，抛物运动都是匀变速曲线运动．）（四）物体做曲线运动的条件：物体所受的合外力的方向与速度方向不在同一直线上，也就是加速度方向与速度方向不在同一直线上．（只要物体的合外力是恒力，它一定做匀变速运动，可能是直线运动，也可能是曲线运动）当物体受到的合外力方向与速度方向的夹角为锐角时，物体做曲线运动的速率将增大；当物体受到的合外力方向与速度方向的夹角为钝角时，物体做曲线运动的速率将减小；当物体受到的合外力方向与速度的方向垂直时，该力只改变速度方向，不改变速度的大小．（五）曲线运动的轨迹做曲线运动的物体，其轨迹向合外力所指一方弯曲，若已知物体的运动轨迹，可判断出物体所受合力的大致方向．速度和加速度在轨迹两侧，轨迹向力的方向弯曲，但不会达到力的方向．（六）运动的合成与分解的方法1、合运动与分运动的定义如果物体同时参与了几个运动，那么物体实际发生的运动就是合运动，那几个运动就是分运动．物体的实际运动一定是合运动，实际运动的位移、速度、加速度就是它的合位移、合速度、合加速度，而分运动的位移、速度、加速度是它的分位移、分速度、分加速度．2、合运动与分运动的关系3、合运动与分运动的求法运动的合成与分解的方法：运动的合成与分解是指描述运动的各物理量，即位移、速度、加速度的合成与分解，由于它们都是矢量，遵循平行四边形定则（或进行正交分解）．(1)如果两个分运动都在同一条直线上，需选取正方向，与正方向同向的量取“＋”，与正方向反向的量取“－”，则矢量运算简化为代数运算．(2)如果两个分运动互成角度，则遵循平行四边形定则(如图所示)．(3)两个相互垂直的分运动的合成：如果两个分运动都是直线运动，且互成角度为90°，其分位移为s 1、s 2，分速度为v 1、v 2，分加速度为a 1、a 2，则其合位移s 、合速度v 和合加速度a ，可以运用解直角三角形的方法求得，如图所示．合位移大小和方向为s ＝，tan θ＝. 合速度大小和方向为v ＝，tan φ＝. 合加速度的大小和方向为：a ＝，tan α＝.(4)运动的分解方法：理论上讲一个合运动可以分解成无数组分运动，但在解决实际问题时不可以随心所欲地随便分解．实际进行运动的分解时，需注意以下几个问题：①确认合运动，就是物体实际表现出来的运动．②明确实际运动是同时参与了哪两个分运动的结果，找到两个参与的分运动．③正交分解法是运动分解最常用的方法，选择哪两个互相垂直的方向进行分解是求解问题的关键． 特别提醒a 合运动一定是物体的实际运动(一般是相对于地面的)．b 不是同一时间内发生的运动、不是同一物体参与的运动不能进行合成．c 对速度进行分解时，不能随意分解，应该建立在对物体的运动效果进行分析的基础上．d 合速度与分速度的关系当两个分速度v 1、v 2大小一定时，合速度的大小可能为：|v 1－v 2|≤v ≤v 1＋v 2，故合速度可能比分速度大，也可能比分速度小，还有可能跟分速度大小相等．4、运动的合成与分解是研究曲线运动规律最基本的方法，它的指导思想就是化曲为直，化变化为不变，化复杂为简单的等效处理观点．在实际问题中应注意对合运动与分运动的判断．合运动就是物体相对于观察者所做的实际运动，只有深刻挖掘物体运动的实际效果，才能正确分解物体的运动．（七）如图所示，用v 1表示船速，v 2表示水速．我们讨论几个关于渡河的问题． θsin d s =。

一． 运动图象1.位移—时间图象（s —t 图）：在平面直角坐标系中用纵轴表示位移，横轴表示时间所作的图像，简称位移图像①物理意义：表示做直线运动的物体，位移随时间的变化规律。

而不是物体的运动轨迹。

②斜率k 表示物体的运动速度，即k=tan α=v 。

交点表示某时刻物体在相同的位置。

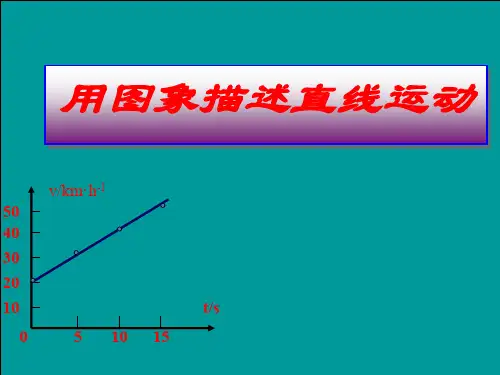
2.速度—时间图像（v —t 图）：在平面直角坐标系中用纵轴表示速度，横轴表示时间所作的图像，简称速度图像。

物理意义：表示作直线运动的物体，速度随时间的变化规律。

①速直线运动的v —t 图像；是一条平行于时间轴的直线。

速度的大小可以直接从图像中看出，位移由s= v 0 t 求出，也可由图像求。

在图像中，图线和坐标轴包围的“面积”在数值上等于位移的大小。

②匀变速直线运动的v —t 图像：是一条倾斜的直线。

斜率k 表示物体运动的加速度。

即k= tan α=a 。

由图像可直接读出初速度v 0的大小，位移由s= v 0t+12 at 2求出，也可由图像求，在图像中图线和坐标轴包围的“面积”在数值上等于位移的大小。

3.形状一样的图线，在不同图象中所表示的物理规律不同，因此在应用时要注意图象的纵、横轴所描述的是什么物理量，图1是形状一样的图线在s-t 图象及v-t 图象中的比较：例１ 如图2，是一质点的位移时间图象，下列说法正确的是：（ ）Ａ.质点做匀减速直线运动 Ｂ.质点做匀速直线运动Ｃ.0—1秒内向正向运动，1—2秒内向负向运动 Ｄ.质点在2秒内的位移为零Ｅ.质点在2秒时的位移为-5米例２ 如图3所示，为一物体作匀变速直线运动的速度图线，根据图线作出的以下几个图1图2判断中，正确的是：（ ）Ａ.物体始终沿正方向运动Ｂ.物体先沿负方向运动，在t=2秒后开始沿正方向运动 Ｃ.在t=2秒前物体位于出发点负方向上，在t=2秒后位于出发点正方向上Ｄ.在t=2秒时，物体距出发点最远 例３ 如图4，一个以初速v ０的沿直线运动的物体的速度图象，末速度为v t ，关于物体在这段时间内的平均速度和加速度a 说法正确的是：（ ）Ａ.2v v v t 0+>B. 2v v v t0+< Ｃ.a 随时间增加 Ｄ.a 随时间减小【练习题】1．图5为直线运动质点的v-t 图象，设开始时在坐标原点，则有：（ ） Ａ.t=t １时，质点离开原点的位移最大 Ｂ.t=t ３时，质点离开原点的位移为负Ｃ.０到t １和t ３到t ４这两段时间里，质点所受合外力的方向相同 Ｄ.t １至t ２和t ２至t ３这两段时间里，质点所受合外力的方向相同2．某物体运动的位移—时间图象如图6所示，则物体：（ ） Ａ.往复运动Ｂ.匀变速直线运动Ｃ.朝某一方向直线运动 Ｄ.不能确定物体的运动情况3．某物体运动的v-t 图象如图7所示，则物体：（ ） Ａ.往复运动Ｂ.匀变速直线运动 Ｃ.朝某一方向直线运动 Ｄ.不能确定图3 图5图 6图7图44．物体在粗糙的水平面上运动，其位移—时间图线如图8所示，已知在沿运动方向上的作用力为Ｆ，物体在运动过程中受的滑动摩擦力为f ，由图线可知：（ ）Ａ.F ＞f Ｂ.F=f Ｃ.F ＜f Ｄ.不能确定5．图9中能正确反映竖直上抛运动的图线是：（ ）6．甲、乙、丙三物体同时从同一地点出发做直线运动，运动情况如图10所示，在20s 时间内，做匀速直线运动的是_______,甲物体运动的路程是_______m,丙物体的平均速度大小是_______m/s.7．一个物体向上竖直抛出，如果在上升阶段和下降阶段所受的空气阻力数值相等，那么在图10中哪一个能够正确反映它的速度变化（以向上方向为正方向）？：（ ）8．在上题中，它的速率—时间图象是图11中的：（ ）9．在同一地，甲、乙两物体沿同一方向作直线运动的速度——时间图象如图12所示，则：（ ）Ａ.两物体两次相遇的时间是１秒和４秒 Ｂ.４秒后甲在乙的前面Ｃ.乙物体先向前运动２秒，再向后运动４秒 Ｄ.两物体相遇两次，相遇的时间为２秒和６秒10．如图13，两光滑斜面的总长度相等，高度也相等，两球由静止从顶端下滑，若球在图上转折点无能量损失，则有：（ ）Ａ.两球同时落地图12图9图11图10 图8Ｂ.b 球先落地Ｃ.两球落地时速率相等 Ｄ.a 球先落地11．一质点由Ａ从静止出发沿直线ＡＢ运动，先作加速度大小为a １的匀加速运动，后以大小为a ２的加速度作匀减速运动，至Ｂ点时速度恰好为零，已知Ａ、Ｂ相距为s ，求证全程所需的时间为：2121a a /s 2)a a (t +=（提示：此题有两种简捷解法，①图象法，在v-t 图上分析计算；②利用平均速度公式2v v v t0+=对前后两段及全程分析。