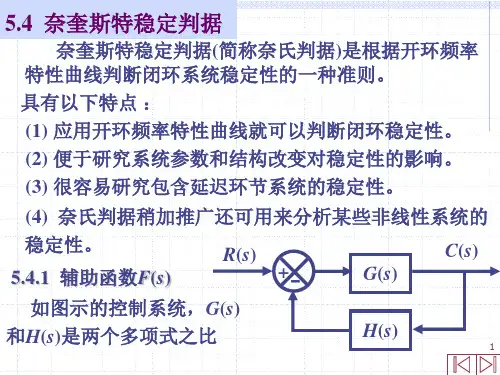
5.4 频域稳定判据5.4.1 奈奎斯特稳定判据闭环控制系统稳定的充要条件是：闭环特征方程的根均具有负的实部，或者说，全部闭环极点都位于左半s 平面。
第3章中介绍的劳斯稳定判据，是利用闭环特征方程的系数来判断闭环系统的稳定性。
这里要介绍的频域稳定判据则是利用系统的开环频率特性)(ωj G 来判断闭环系统的稳定性。
频域稳定判据是奈奎斯特于1932年提出的，它是频率分析法的重要内容。
利用奈奎斯特稳定判据，不但可以判断系统是否稳定（绝对稳定性），也可以确定系统的稳定程度（相对稳定性），还可以用于分析系统的动态性能以及指出改善系统性能指标的途径。
因此，奈奎斯特稳定判据是一种重要而实用的稳定性判据，工程上应用十分广泛。
1．辅助函数对于图5-33所示的控制系统结构图，其开环传递函数为)()()()()(0s N s M s H s G s G == （5-59）相应的闭环传递函数为 )()()()()(1)()(1)()(000s M s N s G s N s N s G s G s G s +=+=+=Φ （5-60） 式中，为开环传递函数的分子多项式，阶；为开环传递函数的分母多项式，阶，。
由式(5-59)、式(5-60)可见，)(s M m )(s N n m n ≥)()(s M s N +和分别为闭环和开环特征多项式。
现以两者之比构成辅助函数)(s N ()()()1()()M s N s F s G s N s +==+ （5-61） 实际系统传递函数分母阶数n 总是大于或等于分子阶数，因此辅助函数的分子、分母同阶，即其零点数与极点数相等。
设)(s G m 1z −，2z −，…，n z −和1p −，，…，分别为其零、极点，则辅助函数可表示为2p −n p −)(F s )())(()())(()(2121n n p s p s p s z s z s z s s F ++++++=L L（5-62）综上所述可知，辅助函数具有以下特点：)(s F （1）辅助函数是闭环特征多项式与开环特征多项式之比，其零点和极点分别为闭环极点和开环极点。
)(s F （2）的零点和极点的个数相同，均为个。
)(s F n （3）与开环传递函数之间只差常量1。
)(s F )(s G )(1)(s G s F +=的几何意义为：F 平面上的坐标原点就是G 平面上的（0,1j −）点，如图5-34所示。
2．幅角定理辅助函数是复变量的单值有理复变函数。
由复变函数理论可知，如果函数在平面上指定域内是非奇异的，那么对于此区域内的任一点d ，都可通过的映射关系在平面上找到一个相应的点 (称为d 的像)；对于平面上的任意一条不通过任何奇异点的封闭曲线)(s F s )(s F s )(s F )(s F 'd 'd s )(s F Γ，也可通过映射关系在平面(以下称)(s F Γ平面)找到一条与它相对应的封闭曲线 (称为的像)，如图5-35所示。
'Γ'ΓΓ图5-35 平面与平面的映射关系s F 设平面上不通过任何奇异点的某条封闭曲线s )(s F Γ，它包围了在平面上的)(s F s Z 个零点和P 个极点。
当以顺时针方向沿封闭曲线s Γ移动一周时，则在平面上相对应于封闭曲线的像将以顺时针的方向围绕原点旋转F Γ'ΓR 圈。
R 与Z 、的关系为P P Z R −= （5-63）3．奈奎斯特稳定判据为了确定辅助函数位于右半平面内的所有零、极点数，现将封闭曲线扩展为整个右半平面。
为此，设计)(s F s Γs Γ曲线由以下3段所组成：ⅰ– 正虚轴ωj s =：频率ω由0变到∞；ⅱ–半径为无限大的右半圆：θj e R s =∞→R ，θ由2π变化到2π−；ⅲ– 负虚轴ωj s =：频率ω由∞−变化到0。
这样，3段组成的封闭曲线（称为奈奎斯特路径，简称奈氏路径）就包含了整个右半平面，如图5-36所示。
Γs 图5-36 奈奎斯特路径在平面上绘制与F Γ相对应的像'Γ：当沿虚轴变化时，由式（5-61）则有s )(1)(ωωj G j F += （5-64）式中，)(ωj G 为系统的开环频率特性。
因而将由下面几段组成：'Γ ⅰ– 和正虚轴对应的是辅助函数的频率特性)(ωj F ，相当于把)(ωj G 右移一个单位；ⅱ–和半径为无穷大的右半圆相对应的辅助函数。
由于开环传递函数的分母阶数高于分子阶数，当时，，故有1)(→s F ∞→s 0)(→s G 1)(1)(→+=s G s F ；ⅲ–和负虚轴相对应的是辅助函数频率特性)(ωj F 对称于实轴的镜像。
图5-37绘出了系统开环频率特性曲线)(ωj G 。
将曲线右移一个单位，并取镜像，则成为平面上的封闭曲线F 'Γ如图5-38所示。
图中用虚线表示镜像。
对于包含了整个右半平面的奈氏路径来说，式（5-63）中的s Z 和P 分别为闭环传递函数和开环传递函数在右半平面上的极点数，而s R 则是平面上F 'Γ曲线顺时针包围原点的圈数，也就是平面上系统开环幅相特性曲线及其镜像顺时针包围（G 0,1j −）点的圈数。
在实际系统分析过程中，我们一般只绘制开环幅相特性曲线不绘制其镜像曲线，考虑到角度定义的方向性，有N R 2−= （5-65） 其中，是开环幅相特性曲线N )(ωj G （不包括其镜像）包围G 平面（0,1j −）点的圈数（逆时针为正，顺时针为负）。
将式（5-65）代入式（5-63），可得奈奎斯特判据（简称奈氏判据）：N P Z 2−= （5-66）式中，Z 是右半平面中闭环极点的个数，是右半平面中开环极点的个数，是G 平面上s P s N )(ωj G 包围（0,1j −）点的圈数（逆时针为正）。
显然，只有当时，闭环系统才是稳定的。
2=−=N P Z .图5-37 )(ωj G 特性曲线 图5-38 平面上的封闭曲线F 例5-9 设系统开环传递函数为)52)(2(52)(2+++=s s s s G试用奈氏判据判定闭环系统的稳定性。
图5-39幅相特性曲线及其镜像解 绘出系统的开环幅相特性曲线如图5-39所示。
当0=ω时，曲线起点在实轴上2.5)0(=j G 。
当∞→ω时，终点在原点。
当5.2=ω时曲线和负虚轴相交，交点为。
当06.5j −3=ω时，曲线和负实轴相交，交点为0.2−。
见图5-39中实线部分。
在右半平面上，系统的开环极点数为0。
开环频率特性s )(ωj G 随着ω从变化到0∞+时，顺时针方向围绕点（）一圈，即0,1j −1−=N 。
用式（5-66）可求得闭环系统在右半平面的极点数为 s 2)1(202=−×−=−=N P Z所以闭环系统不稳定。
利用奈氏判据还可以讨论开环增益K 对闭环系统稳定性的影响。
当K 值变化时，幅频特性成比例变化，而相频特性不受影响。
因此，就图5-39而论，当频率3=ω时，曲线与负实轴正好相交在（0,2j −）点，若K 缩小一半，取6.2=K 时，曲线恰好通过点（），这是临界稳定状态；当时，幅相特性曲线0,1j −6.2<K )(ωj G 将从点（0,1j −）的右方穿过负实轴，不再包围点（），这时闭环系统是稳定的。
0,1j −例5-10 系统结构图如图5-40所示，试判断系统的稳定性并讨论K 值对系统稳定性的影响。
图5-40 例5-10系统结构图 图5-41 1>K和1<K 时的幅相特性曲线 解 系统是一个非最小相角系统，开环不稳定。
开环传递函数在右半平面上有一个极点， s 1=P 。
幅相特性曲线如图5-41所示。
当0=ω时，曲线从负实轴点（）出发；当0,j K −∞→ω时，曲线以趋于坐标原点；幅相特性包围点（o 90−0,1j −）的圈数与N K 值有关。
图5-41绘出了1>K 和1<K 的两条曲线，可见：当1>K 时，曲线逆时针包围了点（0,1j −）的21圈，即21=N ，此时0)21(212=×−=−=N P Z ，故闭环系统稳定；当1<K 时，曲线不包围点（），即，此时0,1j −0=N 10212=×−=−=N P Z ，有一个闭环极点在右半平面，故系统不稳定。
s 5.4.2 奈奎斯特稳定判据的应用如果开环传递函数在虚轴上有极点，则不能直接应用图5-36所示的奈氏路径，因为幅角定理要求奈氏轨线不能经过的奇点，为了在这种情况下应用奈氏判据，可以对奈氏路径略作修改。
使其沿着半径为无穷小（）的右半圆绕过虚轴上的极点。
例如，当开环传递函数中有纯积分环节时，s平面原点有极点，相应的奈氏路径可以修改如图5-42所示。
图中的小半圆绕过了位于坐标原点的极点，使奈氏路径避开了极点，又包围了整个右半平面，前述的奈氏判据结论仍然适用，只是在画幅相特性曲线时，s 取值需要先从绕半径无限小的圆弧逆时针转到，然后再沿虚轴到)(s G )(s F 0→r s 0j o 90+0j ∞j 。
这样需要补充小圆弧所对应的+→=00j j s )(ωj G 特性曲线。
图5-42 开环含有积分 环节时的奈氏路径设系统开环传递函数为 11(1()(1m i i n v v j j K s G s s T s τ=−=))+=+∏∏ 式中，v 为系统型别。
当沿着无穷小半圆逆时针方向移动时，有0lim jv r s re θ→=，映射到G 平面的曲线可以按下式求得001lim 01lim (1)()lim (1)j r j r m i jv jv i n v vs re r v j j s re K s K G s e e r s T s θθθθτ→→−=−=→==+==+∏∏−=∞ （5-67） 由上述分析可见，当沿小半圆从s 0=ω变化到时，+=0ωθ角沿逆时针方向从0变化到2π，这时G 平面上的映射曲线将从)0(j G ∠位置沿半径无穷大的圆弧按顺时针方向转过2v π−角度。
在确定)(ωj G 绕点)01(j ，−圈数的值时，要考虑大圆弧的影响。
N 例5-11 已知开环传递函数为)1()(+=Ts s K s G 其中，T ，绘制奈氏图并判别系统的稳定性。
0>K 0>解 该系统在坐标原点处有一个极点，为Ⅰ型系统。
取奈氏路径如图5-42所示。
当沿小半圆移动从)(s G s 0=ω变化到时，在平面上映射曲线为半径的+=0ωG ∞→R 2π圆弧。
幅相特性曲线（包括大圆弧）如图5-43所示。
此系统开环传递函数在右半平面无极点，；的奈氏曲线又不包围点（s 0=P )(s G 0,1j −），0=N ；因此02=−=N P Z ，闭环系统是稳定的。
图5-43 例5-11的奈氏图 图5-44 例5-12的奈氏图例5-12 已知系统开环传递函数为)1()3()()(−+=s s s K s H s G 试绘制奈氏图，并分析闭环系统的稳定性。
