九年级数学上册 201 二次函数课后零失误训练 北京课改版

反比例函数的图象和性质课后作业1. 姜教师给出一个函数表达式，甲. 乙. 丙三位同窗别离正确指出了那个函数的一个性质. 甲：函数图象通过第一象限；乙：函数图象通过第三象限；丙：在每一个象限内，y 值随x 值的增大而减小. 依照他们的描述，姜教师给出的那个函数表达式可能是（ ）A. y=3xB. y ＝x 3C. y ＝−x 4D. y=x 22. 已知反比例函数y=-x 2，以下结论不正确的选项是（ ）A. 图象必通过点（-1，2）B. y 随x 的增大而增大C. 图象在第二、四象限内D. 假设x ＞1，那么0＞y ＞-23. 在同一坐标系中，函数y=ax 2+bx 与y=x b的图象大致是图中的（ ）A. B. C. D.4. 对反比例函数y ＝x 4，以下说法不正确的选项是（ ）A. 它的图象在第一、三象限B. 点（-1，-4）在它的图象上C. 当x ＜0时，y 随x 的增大而减小D. 当x ＞0时，y 随x 的增大而增大5. 在反比例函数y ＝x k-1的每一条曲线上，y 都随着x 的增大而减小，那么k 的值能够是（）A. -1B. 1C. 2D. 36. 反比例函数y=x k 12+（k 为常数）的图象位于（ ）A. 第一、二象限B. 第一、三象限C. 第二、四象限D. 第三、四象限7. 表示关系式①|y|=x 1，②y=x 1，③y=-x 1；④|y|=x 1的图象依次是8. 假设y 是x 的反比例函数，而且当x ＜0时，y 随x 的增大而增大，那么它的解析式可能是 （写出一个符合条件的解析式即可） 9. 已知反比例函数y=xk （k 是常数，k≠0），当x ＜0时，y 随着x 的增大而增大，那么那个反比例函数的解析式是 （写出一个即可）.10. 已知反比例函数y=（m-2）x m 2−m −7.（1）当反比例函数的图象位于第一、三象限时，求m 的值？（2）当反比例函数的图象位于第二、四象限时，求m 的值？11. 已知反比例函数y=xn 8-（m 为常数） （1）假设函数图象通过点A （-1，6），求m 的值；（2）假设函数图象在二、四象限，求m 的取值范围；（3）假设x ＞0时，y 随x 的增大而减小，求m 的取值范围.12. 已知常数a （a 是整数）知足下面两个要求：①关于x 的一元二次方程ax 2+3x-1=0有两个不相等的实数根；②反比例函数y ＝x a 22+的图象在二、四象限. （1）求a 的值；（2）在所给直角坐标系顶用描点法画出y ＝xa 22+的图象，并依照图象写出： 当x ＞4时，y 的取值范围是 ；当y ＜1时，x 的取值范围是 .反比例函数的图象和性质课后作业参考答案1. 解析：能够别离写出选项中各个函数图象的特点，与题目描述相符的即为正确的，不符的确实是错误的，此题得以解决.解：y=3x 的图象通过一、三象限过原点的直线，y 随x 的增大而增大，应选项A 错误；y ＝x 3的图象在一、三象限，在每一个象限内y 随x 的增大而减小，应选项B 正确； y ＝−x 1的图象在二、四象限，应选项C 错误； y=x 2的图象是极点在原点开口向上的抛物线，在一、二象限，应选项D 错误；应选B.2. 解析：依照反比例函数的性质：当k ＜0，双曲线的两支别离位于第二、第四象限，在每一象限内y 随x 的增大而增大进行分析即可.解：A. 图象必通过点（-1，2），说法正确，不合题意；B. k=-2＜0，每一个象限内，y 随x 的增大而增大，说法错误，符合题意；C. k=-2＜0，图象在第二、四象限内，说法正确，不合题意；D. 假设x ＞1，那么-2＜y ＜0，说法正确，不符合题意；应选：B3.解析：依照反比例函数和二次函数的图象得出b 的范围，看看是不是相同即可.解：A. 依照反比例函数得出b ＞0，依照二次函数得出a ＞0，b ＜0，因此b 的范围不同，故本选项错误；B. 依照反比例函数得出b ＞0，依照二次函数得出a ＜0，b ＜0，因此b 的范围不同，故本选项错误；C. 依照反比例函数得出b ＜0，依照二次函数得出a ＞0，b ＞0，因此b 的范围不同，故本选项错误；D. 依照反比例函数得出b ＞0，依照二次函数得出a ＜0，b ＞0，因此b 的范围相同，故本选项正确；应选D4. 解析：依照反比例函数的性质用排除法解答.解：A. ∵k=4＞0，∴图象在第一、三象限，正确，故本选项不符合题意；B. 当x=-1时，y ＝x4=-4，正确，故本选项不符合题意；C. ∵k=4＞0，∴当x ＜0时，y 随x 的增大而减小，正确，故本选项不符合题意；D. ∵k=4＞0，∴当x ＞0时，y 随x 的增大而减小，错误，故本选项符合题意.应选D.5. 解析：利用反比例函数的增减性，y 随x 的增大而减小，那么求解不等式1-k ＞0即可.6解：∵反比例函数y ＝x k -1图象的每一条曲线上，y 随x 的增大而减小， ∴1-k ＞0，解得k ＜1.应选A.6. 解析：先依照一个数的平方为非负数的特点确信比例系数，再利用反比例函数的性质求解.解：∵k 2+1≥1＞0， ∴反比例函数y=x k 12+（k 为常数）的图象位于第一、三象限. 应选B.7. 解析：一一对照函数的图象和解析式，利用函数的性质即可解答.解：①|y|=x1对应C ，②y=x 1对应B ，③y=-x 1对应D ；④|y|=x 1对应A. 故答案为C ，B ，D ，A.8. 解析：反比例函数的图象在每一个象限内，函数值y 随自变量x 的增大而增大，那么反比例函数的反比例系数k ＜0；反之，只要k ＜0，那么反比例函数在每一个象限内，函数值y 随自变量x 的增大而增大. 解：只要使反比例系数小于0即可. 如y=-x 1（x ＜0），答案不唯一. 答案可为：y=-x1（x ＜0）. 9. 解析：依照“当x ＜0时，y 随着x 的增大而增大”，可得出反比例函数在x ＜0时，是增函数，由此得出k ＜0，随意写出一个k 值即可得出结论.解：∵当x ＜0时，y 随着x 的增大而增大，∴反比例函数y=x k （k 是常数，k≠0）在x ＜0时，是增函数， ∴k ＜0.故答案为：y=-x1 10. 解析：（1）依照反比例函数的概念和性质列出方程求解即可.（2）依照反比例函数的概念和性质列出方程求解即可解：（1）依照题意得：m −2＞0 ，m 2−m −7＝−1 解得：m=3；（2）依照题意得：m −2＜0，m 2−m −7＝0 解得：m=-211. 解析：（1）将点A 的坐标代入即可求得m 的值；（2）依照图象所处的象限确信m 的取值范围即可；（3）依照增减性确信m-8的符号，从而确信m 的取值范围.解：（1）∵函数图象通过点A （-1，6），∴m-8=xy=-1×6=-6，解得：m=2，∴m 的值是2；（2）∵函数图象在二、四象限，∴m-8＜0，解得：m ＜8，∴m 的取值范围是m ＜8；（3）∵假设x ＞0时，y 随x 的增大而减小，∴m-8＞0，解得：m ＞8，∴m 的取值范围是m ＞8；12. 解析：1）先依照关于x 的一元二次方程ax 2+3x-1=0有两个不相等的实数根求出a 的取值范围，再由反比例函数y ＝x a 22 的图象在二，四象限得出a 的取值范围，由a 为整数即可得出a 的值； （2）依照a 的值得出反比例函数解析式，画出函数图象，由函数图象即可得出结论.解：（1）∵方程有两个不相等的实数根，∴△=9+4a ＞0，得a ＞-49且a≠0； ∵反比例函数图象在二，四象限，∴2a+2＜0，得a ＜-1，∴-49＜a ＜-1. ∵a 是整数，∴a=-2；（2）∵a=-2，∴反比例函数的解析式为y=-x2， 其函数图象如下图；当x ＞4时，y 的取值范围-21＜y ＜0；当y ＜1时，x 的取值范围是 x ＜-2或x ＞0. 故答案为：-21＜y ＜0，x ＜-2或x ＞0。

20.2二次函数y=ax2+bx+c(a ≠0)的图象零失误训练基础能力训练★回归教材 注重基础 ◆二次函数y =ax 2+bx +c (a ≠0)的图象1.已知函数y =mx m 2+m ，当m =_____时，它的图象是开口向上的抛物线.2.已知抛物线221x y =的图象经过点(a ，4.5)和(－a ，y 1)，则y 1的值是_____.3.函数6)3(212++-=x y 的开口方向是______，对称轴是______，顶点坐标是_______.4.抛物线y =x 2－2x －3的对称轴是______，顶点坐标是______.5.二次函数253212++=x x y 的图象由函数221x y =的图象先向_____平移_____个单位长度，再向_____平移_____个单位长度得到的. 6.二次函数y =ax 2+bx +c 中，a >0，b <0，c =0，则其图象的顶点应在第_____象限.7.抛物线y =x 2－2mx +m +2的顶点坐标在第三象限，则m 的取值范围为_____.8.已知二次函数y =x 2－2x －3的图象与x 轴交于A .B 两点，在x 轴上方，抛物线上有一点C ，且△ABC 的面积等于10，则C 点的坐标为______.9.已知二次函数y =ax 2与一次函数y =3x －4的图象都经过(b ，2)，则a =_____，b =_____；试写出一个经过(a ，b )点的抛物线的表达式_______.10.函数y =ax 2+bx +c 的图象与y =2x 2－3x －1的图象形状.大小相同，开口方向相反，则下面结论正确的是( )A.a=2，6=3，c=1B.a=－2，b.c为任意实数C.b=3，a.c为任意实数D.c=1，a.b为不等于0的实数11.(2008·长春)二次函数y=kx2－6x+3的图象与x轴有交点，则k 的取值范围是( )A.k>3B.k>3且k≠0C.k≤3D.k≤3且k≠012.已知y=ax2+bx+c的图象如图20－2－4所示，则a.b.c的值满足( )A.a<0，b>0，c>0B.a<0，b>0，c<0C.a<0，b<0，c>0D.a<0，b<0，c<013.如图20－2－5，一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象大致是( )14.已知二次函数y =a (x +h )2+k 的图象如图20－2－6所示，则一次函数y =ax +hk 的图象不经过哪个象限?15.用配方法求二次函数45351252+-=x x y 图象的顶点坐标和对称轴.16.巳知点A (－2，－c )向右平移8个单位得到点A ′，A 与A ′两点均在抛物线y =ax 2+bx +c 上，且这条抛物线与y 轴交点的纵坐标为－6，求这条抛物线的顶点坐标.17.画出函数y =x 2+x －2的图象，并根据图象回答下列问题: (1)求抛物线与坐标轴交点的坐标；(2)当x 取何值时，y >0?当x 取何值时，y <0?(3)当x 取何值时，y 随x 的增大而增大?x 取何值时，y 随x 的增大而减小?(4)求抛物线y=x2+x－2的对称轴；(5)该函数有最大值还是有最小值?x取何值时，y有最大值(或最小值)?最大值(或最小值)是多少?综合创新训练★登高望远课外拓展◆创新应用18.某市场经营一批进价为2元一件的商品，在市场调查中发现此商品的销售单价x(元)与日销售量y(件)之间有如下关系:销售单价x(元) 3 5 9 11 销售量y(件) 18 14 6 2描出实数对(x，y)的对应点；②猜测并确定日销售量y(件)与日销售单价x(元)之间的函数关系式，画出图象.(2)设经营此商品的日销售利润(不考虑其他因素)为P元，根据日销售量规律:①试求出日销售利润P元与日销售单价x元之间的函数关系式，并求出日销售利润的最大值，试问日销售利润P是否存在最小值?若有，请求出；若无，请说明理由.②在给定的直角坐标系中，画出日销售利润P元与日销售单价x元之间的函数图象简图，观察图象，写出x.P的取值范围.◆开放探索19.阅读材料，解答问题. 阅读材料:当抛物线的函数关系式中含有字母系数时，随着系数中的字母的取值不同，抛物线的顶点坐标也将发生变化.例如:由抛物线y =x 2－2mx +m 2+2x －1， ① 有y =(x －m )2+2m －1， ② ∴抛物线的顶点坐标为(m ，2m －1).即⎩⎨⎧-==.12,m y m x ④③ 当m 的值变化时，x .y 的值也随之变化，因而y 的值随x 值的变化而变化，将③代人④得，y =2x －1. ⑤可见，不论m 取任何实数，抛物线的顶点的纵坐标y 与横坐标x 都满足关系式:y =2x －1. 解答问题:(1)在上述过程中，由①到②所用的数学方法是_______，其中运用了_______公式，由③④得到⑤所用的数学方法是______.(2)根据阅读材料提供的方法，确定抛物线y =x 2－2mx +2m 2－3m +1顶点的纵坐标y 与横坐标x 之间的关系式.参考答案1答案:1 解析:由题意知，该函数为二次函数，所以m 2+m =2，解得m 1=－2，m 2=1，又因为图象开口向上，所以m =－2舍去，只取m =1.2答案:4.5 解析:由题意知2215.4a =，a 2=9，a =±3，将(－a ，y 1)代入221x y =，进一步求得y 1=4.5. 3答案:向下 x =－3 (－3，6)4答案:x =1 (1，－4) 解析:利用配方法可以得到结论，也可直接用对称轴和顶点坐标公式来求出结果.5答案:左 3 下2 解析:由2)3(2125)6(2125321222-+=++=++=x x x x x y 及221x y =可知平移情况. 6答案:四 解析:由02>-=abx ，044422<-=-a b a b ac 可知抛物线的顶点必须在第四象限.7答案:m <－1 解析:易得顶点坐标为(m ，－m 2+m +2).∵顶点在第三象限，∴⎩⎨⎧<++-<,02,02m m m解不等式组得:m <－1. 8答案:(4，5)或(－2，5)解析:因为二次函数与x 轴相交，所以令x 2－2x －3=0，解得x 1=－1，x 2=3，所以AB 之间的距离为4，S △ABC =21×4×h =10，得h =5，即点C的纵坐标为5，所以有5=x 2－2x －3，解得:x 1=－2，x 2=4，所以C 点坐标为(4，5)或(－2，5).9答案:212 y =8x 2(答案不唯一) 解析:直接代入，先求b ，再进一步求a ，符合条件的表达式可以由y =8x 2，21102-=x y 等(答案不唯一). 10答案:B11答案:D 解析:由题意知:⎩⎨⎧≠≥-0042k ac b 即⎩⎨⎧≠≥⨯⨯--0034)6(2k k 解得k ≤3且k ≠0.注意:这里与x 轴也可能只有一个交点，因此勿忘b 2－4ac =0的情况. 12答案:A 解析:因为图象开口向下，所以a <0.又因为抛物线与y 轴的交点在正半轴上，所以c >0.又因为02>-ab，所以b >0，故选A 13答案:D14答案:解析:由二次函数y =a (x +h )2+k 的图象可知，因为抛物线的开口向上，所以a >0，因为抛物线的对称轴在y 轴的左侧，所以h >0，又因为抛物线与y 轴的交点在x 轴下方，所以k <0，所以hk <0，由此可知，直线y =ax +hk 经过第一.三.四象限，则一次函数y =ax +hk 的图象不经过第二象限. 15答案:解析:)34(125453512522+-=+-=x x x x y 125)2(125]1)2[(12522--=--=x x ， ∴该函数图象的顶点坐标是(2，125-)，对称轴是x =2. 16答案:解析:抛物线的解析式是y =x 2－4x －6，顶点坐标为(2，－10). 17答案:解析:(1)与x 轴交点坐标是(－2，0)和(1，0)，与y 轴交点的坐标是(0，－2).(2)当x <－2或x >1时，y >0，－2<x <1时，y <0.(3)当x >21-时，y 随x 的增大而增大，当x <21-时，y 随x 的增大而减小.(4)对称轴为直线21-=x .(5)有最小值，当21-=x 时，49－最小值=y . 18答案:解析:(1)①如图所示.②函数关系式为y =－2x +24(0≤x ≤12)，函数图象如图a 所示. (2)①因为销售利润=售价－进货价，所以P =xy －2y .又因为y =－2x +24，所以P =y (x －2)=(－2x +24)(x －2)=－2(x －7)2+50.所以当x =7时，P最大=50，又当x >12时，即销售单价大于12元时，此时无人购买，所以此时利润为P =0(x ≥12)，由实际意义知，当销售单价x =0时，此时利润P =－48，即为最小值.②根据实际意义，当0≤x <2时，亏本卖出；当x =－2或x =12时利润P =0；当x >12时，即高价卖，无人购买，此时利润P =0，如图b ，由图象可知x ≥0，－48≤P ≤50.19答案:解析:(1)配方法 完全平方 代入法(2)由m ma b x =⨯--=-=1222，1344)132(4442222+-=-+-=-=m m m m m a b ac y ，把x =m 代入y =m 2－3m +1得y =x 2－3x +1，即为抛物钱y =x 2－2mx +2m 2－3m +1的顶点纵坐标y 与横坐标x 之间的关系式.。

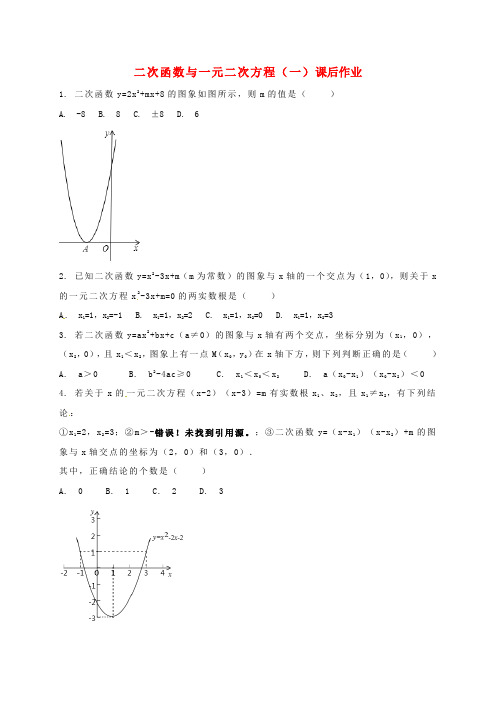
二次函数与一元二次方程（一）课后作业1. 二次函数y=2x2+mx+8的图象如图所示，则m的值是（）A. -8B. 8C. ±8D. 62. 已知二次函数y=x2-3x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x 的一元二次方程x2-3x+m=0的两实数根是（）A. x1=1，x2=-1B. x1=1，x2=2C. x1=1，x2=0D. x1=1，x2=33. 若二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点，坐标分别为（x1，0），（x2，0），且x1＜x2，图象上有一点M（x0，y0）在x轴下方，则下列判断正确的是（）A. a＞0B. b2-4ac≥0C. x1＜x0＜x2D. a（x0-x1）（x0-x2）＜04. 若关于x的一元二次方程（x-2）（x-3）=m有实数根x1、x2，且x1≠x2，有下列结论：①x1=2，x2=3；②m＞-错误！未找到引用源。

；③二次函数y=（x-x1）（x-x2）+m的图象与x轴交点的坐标为（2，0）和（3，0）．其中，正确结论的个数是（）A. 0B. 1C. 2D. 35. 已知函数y=x2-2x-2的图象如图所示，则关于x的一元二次方程x2-2x-2-m=0的两个根为x1和x2且x1＜0，x2＞0．则m的取值范围是（）A. -3≤m≤-2B. -3＜m＜0C. -3＜mD. -2＜m6. 对于抛物线y=-mx2-4mx-n（m≠0）与x轴的交点为A（-1，0），B（x2，0），则下列说法：①一元二次方程mx2+4mx+n=0的两根为x1=-1，x2=-3；②原抛物线与y轴交于C点，CE∥x轴交抛物线于E点，则CE=4；③点D（2，y1），点F（-6，y2）在原抛物线上，则y2≤y1；④抛物线y=mx2+4mx+n与原抛物线关于x轴对称．其中正确的说法有（）A. ①②③④B. ①③④C. ②③D. ①②④7. 二次函数y=ax2+bx+c的图象如图所示，且方程ax2+bx+c=k有两个不相等的实数根，则k的取值范围是（）A. k＜2B. k≤2C.k＜3D. 1＜k＜38. 如图，一次函数y1=kx+n（k≠0）与二次函数y2=ax2+bx+c（a≠0）的图象相交于A （-1，5）、B（9，2）两点，则关于x的不等式kx+n≥ax2+bx+c的解集为（）A. -1≤x≤9 B.-1≤x＜9 C. -1＜x≤9 D.x≤-1或x≥99. 如图是二次函数y=ax2+bx+c的部分图象，由图象可知当y＞0时，x的范围是（）A. x＜-1且x＞5B. x＞5C. -1＜x＜5D. x＜-1或x＞510. 有一次函数y1=kx+m和二次函数y2=ax2+bx+c的大致图象如图，请根据图中信息回答问题（在横线上直接写上答案）（1）不等式ax2+bx+c＜0的解集是_______；kx+m＞ax2+bx+c的解集是_____．（2）当x=_________时，y1=y2．（3）要使y2随x的增大而增大，x的取值范围应是_________．11. 如图，二次函数y=（x-2）2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点．已知一次函数y=kx+b的图象经过该二次函数图象上点A（1，0）及点B．（1）求二次函数与一次函数的解析式；（2）根据图象，写出满足kx+b≥（x-2）2+m的x的取值范围．12. 二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象解答下列问题：（1）写出方程ax2+bx+c=0的两个根；（2）写出不等式ax2+bx+c＞0的解集；（3）写出y随x的增大而减小的自变量x的取值范围；（4）若方程ax2+bx+c=k有两个不相等的实数根，求k的取值范围．二次函数与一元二次方程（一）课后作业参考答案1. B2. B3. D4. C5. D6. D7. A8. A9. C10. 2＜x ＜6 1＜x ＜8 1或8 x ＞411. 解：（1）将点A （1，0）代入y=（x-2）2+m 得（1-2）2+m=0，解得m=-1， 所以二次函数解析式为y=（x-2）2-1；当x=0时，y=4-1=3，所以C 点坐标为（0，3），由于C 和B 关于对称轴对称，而抛物线的对称轴为直线x=2，所以B 点坐标为（4，3），将A （1，0）、B （4，3）代入y =kx+b 得{k+b=04k+b=3所以一次函数解析式为y=x-1； （2）当kx+b≥（x-2）2+m 时，1≤x≤4．12. 解：（1）由图可知，抛物线y=ax 2+bx+c （a≠0）与x 轴交于（1，0）、（3，0）两点．∴x 1=1，x 2=3；（2）依题意因为ax 2+bx+c ＞0，得出x 的取值范围为1＜x ＜3；（3）如图可知，当y 随x 的增大而减小，自变量x 的取值范围为x ＞2； { k=1 b=-1（4）由顶点（2，2）设方程为a（x-2）2+2=0，∵二次函数与x轴的2个交点为（1，0），（3，0），代入a（x-2）2+2=0得：a（1-2）2+2=0，∴a=-2，∴抛物线方程为y=-2（x-2）2+2，y=-2（x-2）2+2-k实际上是原抛物线下移或上移|k|个单位．由图象知，当2-k＞0时，抛物线与x轴有两个交点．故k＜2．。

反比例函数与几何图形的综合性问题（答题时间：30分钟）1. （江苏苏州）如图，菱形OABC 的顶点C 的坐标为（3，4），顶点A 在x 轴的正半轴上。

反比例函数y ＝k x（x ＞0）的图象经过顶点B ，则k 的值为（ ）A. 12B. 20C. 24D. 322. 如图，在平面直角坐标系中，直线y=－3x+3与x 轴、y 轴分别交于A 、B 两点，以AB 为边在第一象限作正方形ABCD ，点D 在双曲线ky x=（k≠0）上。

将正方形沿x 轴负方向平移a 个单位长度后，点C 恰好落在该双曲线上，则a 的值是（ ）A. 1B. 2C. 3D. 4 3. （贵州省黔东南州）如图，直线y=2x 与双曲线y=2x在第一象限的交点为A ，过点A 作AB⊥x 轴于B ，将△ABO 绕点O 旋转90°，得到△A′B′O，则点A′的坐标为（ ）A. （1.0）B. （1.0）或（－1.0）C. （2.0）或（0，－2）D. （－2.1）或（2，－1） 4. 如图，等边三角形OAB 的一边OA 在x 轴上，双曲线y ＝3x在第一象限内的图象经过OB 边的中点C ，则点B 的坐标是（ ）A. （1，3）B. （3，1）C. （2，23）D. （23，2）5. （四川宜宾）如图，直线x y 34=与双曲线)0(>=x x k y 交于点A ，将直线x y 34=向右平移29个单位后，与双曲线)0(>=x x k y 交于点B ，与x 轴交于点C ，若2=BCAO，则k = 。

6. （重庆市（A ））如图，菱形OABC 的顶点O 是坐标原点，顶点A 在x 轴的正半轴上，顶点B 、C 均在第一象限，OA ＝2，∠AOC ＝60°，点D 在边AB 上，将四边形ODBC 沿直线OD 翻折，使点B 和点C 分别落在这个坐标平面内的点B ′和点C ′处，且∠C ′DB ′＝60°。

若某反比例函数的图象经过点B ′，则这个反比例函数的解析式为 。

20.1 二次函数基础能力训练★回归教材 注重基础 ◆二次函数的概念1.已知y=(m 2－1)x m2－m是二次函数,则m=_______. 2.下列函数表达式中不是二次函数的是( )A.y=3(x －1)2－1 B.22x y = C.52-=x y D.y=(x+1)(x －2)◆列二次函数的表达式3.(2008·福州)已知抛物线y=x 2－x －1与x 轴的一个交点为(m,0),则代数式m 2－m+2 008的值为( )A.2 006B.2 007C.2 008D.2 0094.某品牌的空调原价6 000元,如果每年的降价率为x,则两年后这种空调的价位为y 元,那么y 与x 之间的函数关系表达式为( )A.y=6000(1－x)2B.y=6 000(1－x)C.y=6000－x 2D.y=6 000(1+x)25.一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察到小球滚动的距离s(米)与滚则s(米)与t(秒)之间的关系表达式为( )A.y=2tB.y=2t 2+2C.y=2t 2D.y=2(t －1)26.有一个长方体木块,其长和宽相等,高比长多2米.(1)若长方体的长和宽用x(米)表示,则长方体的表面积S(米2)如何表示?(2)如果将长方体的表面涂上油漆,每平方米所需要的费用是5元,那么给每个长方体涂漆的费用用y 元表示,则y 的表达式是什么?(3)如果长方体的长是1米,那么给10个这样的长方体涂漆需要多少费用?7.已知函数k kx x k k y -+++=2)(22.(1)当k 取何值时是二次函数? (2)当k 取何值时是一次函数?综合创新训练★登高望远 课外拓展 ◆创新应用8.银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是中国人民银行根据国民经济发展的情况而决定的,设人民币一年定期储蓄的年利率是x,一年到期后.银行将本金和利息自动按一年定期储蓄转存,如果存款额是l 000元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税).若考虑利息税(利息税是利息的20％)呢?9.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多的利润,商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件,按每件25元销售时,每月能卖210件,假定每月销售的数量y(件)是价格x(元/件)的一次函数. (1)试求y 与x 的函数关系式；(2)如果以每件x 元销售时,每月可获利润为w 元,试写出w 与x 之间的关系式.它是x 的二次函数吗?◆开放探索10.如图20－1－1所示,等腰Rt△ABC 以2米/秒的速度沿直线l 向正方形移动,直到AB 与CD 重合.设x 秒时,三角形与正方形重叠部分的面积为y 米2. (1)写出y 与x 的函数关系表达式.(2)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?11.(2008·湖州)对于二次函数y=ax 2+bx+c,如果当x 取任意整数时,函数值y 都是整数,那么我们把该函数的图象叫做整点抛物线(例如：y=x 2+x+2).(1)请你写出一个二次项系数的绝对值小于1的整点抛物线的解析式(不必证明)； (2)请探索：是否存在二次项系数的绝对值小于21的整点抛物线?若存在,请写出其中一条抛物线的解析式；若不存在,请说明理由.参考答案1答案：2 解析：因为是二次函数，所以m 2－m=2，解得m 1=－1，m 2=2.但当m=－1时，二次项系数m 2－1=0，故舍去，只取m=2. 2答案：C3答案：D 解析：把(m ，0)代人y=x 2－x －1得：m 2－m －1=0，所以m 2－m=1，所以m 2－m+2008=1+2008=2009.4答案：A 解析：因为y=6000(1－x)×(1－x)=6000(1－x)25答案：C 解析：可将表格中数据代人四个选择支试试，也可从表格t 与s 的数量关系中总结出其所具有的特征.6答案：(1)S=6x 2+8x (2)y=30x 2+40x (3)700元解析：对于(1)S=x 2+x 2+x(x+2)×4=6x 2+8x ；对于(2)y=(6x 2+8x)×5=30x 2+40x ； 对于(3)(30×1+40×1)×10=700(元).7答案：解析：(1)由二次函数的定义可知k 2+k ≠0，解得k ≠0且k ≠－1.(2)若为一次函数，则k 2+k=0，解得k 1=0,k 2=－1，但当k=0时，原式变为2y 显然不是一次函数，所以舍去，只取k=－1.8答案：y=1 000x 2+2 000x+1 000(不考虑利息税)y=640x 2+1 600x+1 000(考虑利息税)解析：对于第一种情况：y=1 000(1+x)×(1+x)=1 000(1+x)2整理即得答案； 对于第二种情况，y=1 000x ·(1－20％)+1 000+[1 000x ·(1－20％)+1 000]·x ·(1－20％)，整理得y=640x 2+1 600x+1 000.9答案：解析：(1)设y 与x 的关系式为y=kx+b.由题意知，x=20，y=360和x=25，y=210符合上述关系式，故⎩⎨⎧+=+=,25210,20360b k b k 有解得k=－30，b=960， ∴y 与x 的函数关系式为y=－30x+960. (2)设每月的销售利润为w ，则w=y·(x－16)=(－30x+960)(x －16)w=－30x 2+1440x －15 360. 显然，w 是x 的二次函数.10答案：解析：对于(1)设经过x 秒后的图形如图所示：则CC ′=2x ，△C'CE ∽△C'BA ，所以B C''CC AB CE =,即424x CE =，解得CE=2x ， 所以，y=21CC ′·CE=21·2x ·2x=2x 2. (2)由题意知84421=⨯⨯=y ，即8=2x 2，解得x=±2 (舍负)，取x=2(秒).11答案：解析：(1)如：x x y 21212+=，x x y 21212-=－等等(只要写出一个符合条件的函数解析式即可)(2)假设存在符合条件的抛物线，则对于抛物线y=ax 2+bx+c ，当x=0时，y=c ；当x=1时，y=a+b+c.由整点抛物线定义可知：c 为整数，a+b+c 为整数，所以a+b 必为整数，又当x=2时，y=4a+2b+c=2a+2(a+b)+c 是整数，所以2a 必为整数，从而a 应为21的整数倍，因为a ≠0，所以21||≥a ,所以不存在二次项系数的绝对值小于21的整点抛物线.。

零失误训练基础能力训练★回归教材 注重基础 ◆二次函数的性质1.(2008·兰州)在同一坐标平面内,下列4个函数: ①y =2(x +1)2；②y =2x 2+3；③y =－2x －1；④1212-=x y 的图象不可能由函数y =2x 2+1的图象通过平移变换,轴对称变换得到的函数是_______.(填序号)2.结合函数y =(x －2)2－1的图象,确定当时,y =0；当______时,y >0；当____时,y <0.3.已知二次函数y =x 2－6x +m 的最小值为1,则m =_______.4.抛物线23212-+=x x y 的最低点坐标是______；当______时,y 随x 的增大而增大. 5.若抛物线y =－x 2+bx +c 的最高点为(－1,－3),则b =_____,c =_____. 6.若二次函数y =mx m 2+1的图象有最高点,则m 的值为______. 7.已知函数206212++=x x y . (1)当自变量x 在什么范围内取值时,y 随x 的增大而增大?x 在什么范围内取值时,y 随x 的增大而减小?(2)这个二次函数有最大值或最小值吗?如果有,当x 为何值时,函数取得最大值或最小值?求出最大值或最小值.8.若二次函数y =(1－2m )x 2的图象经过点A (x 1,y 1)和点B (x 2,y 2),当x l <x 2<0时,y 1>y 2,求m 的取值范围.9.(2008·南京)已知二次函数y =x 2+bx +c 中,函数y 与自变量x 的部分对应值如下表:(1)求该二次函数的解析式；(2)当x 为何值时,y 有最小值,最小值是多少?(3)若A (m ,y 1)、B (m +1,y 2)两点都在该函数图象上,试比较y 1与y 2的大小. 综合创新训练★登高望远 课外拓展 ◆创新应用10.二次函数y =x 2+bx +c 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,3),若△ABC 的面积为9,求此二次函数的最小值.11.已知矩形的周长是20,对角线长x .(1)试把矩形的面积S 用关于x 的代数式表示； (2)确定对角线x 的取值范围； (3)当x 何值时,矩形的面积最大? ◆开放探索12.心理学家发现,学生对概念的接受能力随提出概念所用的时间变化而变化.讲课开始时,学生的注意力逐步增加；中问一段时间学生的注意力保持较为理想的状态；随后学生的注意力开始分散,经过实验分析可知,学生的注意力y 随时间t 的变化规律有如下关系式:⎪⎩⎪⎨⎧≤<+-≤<≤<++-=).4020(3807),2010(240),100(100242t t t t t t y (1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中? (2)讲课开始后什么时刻学生的注意力最集中?能持续多少分钟?(3)一道数学难题,需要讲解24分钟,为了使学生的理解效果好,要求学生的注意力最低达到180,那么老师能否经过适当安排,在学生注意力达到所需状态下讲解完这道题目?参考答案1答案:④2答案:x =1或x =3 x >3或x <1 1<x <3 3答案:10 解析:由题意知:1143614=⨯-⨯⨯m ，解得m =10.4答案:(－1，－2) x >－1 解析:求最低点坐标实质上是求顶点坐标. 5答案:－2 －4 解析:利用顶点坐标公式代人分别求解.6答案:－1 解析:由已知条件得，m 2+1=2，故m =±1.又抛物线有最高点，∴m <0，故m 的值为－1.7答案:解析:(1)因为21=a ，b =6，c =20，所以621262-=⨯-=-a b ,2242146202144422==⨯-⨯⨯=-a b ac ,则图象的顶点坐标为(－6，2).因为抛物线开口向上，所以，当x >－6时，y 随x 的增大而增大；当x <－6时，y 随x 的增大而减小.(2)因为抛物线开口向上，顶点坐标为(－6，2)，所以当x =－6时，这个二次函数有最小值2.8答案:解析:显然，该抛物线的对称轴是y 轴，即x =0，由题意知，在对称轴左侧，y 随x 的增大而减小，说明抛物线开口向上，即1－2m >0，解得m <21. 9答案:解析:(1)二次函数的解析式为y =ax 2－4x +5. (2)当x =2时，y 有最小值为1.(3)y 2－y 1=(m +1)2－4(m +1)+5－(m 2－4m +5)=2m －3，当2m －3<0，即m <23时，y 1>y 2；当2m －3=0，即m =23时，y 1=y 2；当2m －3>0，即m >23时，y 1<y 2. 10答案:解析:设A (x 1，0)、B (x 2，0)，则x 1、x 2是方程x 2+bx +c =0的两根.因为y =x 2+bx +c 过点C (0，3)，所以c =3，S △ABC =93||21||||21=∙=∙AB OC AB ,∴6||=AB ，∴|x 1－x 2|=6，即(x 1+x 2)2－4x 1x 2=36，而⎩⎨⎧==∙-=+,3,2121c x x b x x∴b 2－12=36.∴b =±34.则9)32(33422-±=+±=x x x y ，∴所求最小值为－9. 11答案:解析:(1)设矩形两邻边长分别为a 、b ,则 a +b =10，a 2+b 2=x 2，∵(a +b )2=a 2+b 2+2ab ， ∴100=x 2+2S ，∴S =221x -+50. (2)∵x 2=a 2+b 2=a 2+(10－a )2=2a 2－20a +100 ∴当a =5时，x 最小，最小值为25.又由三角形三边关系，得10=+<b a x ,∴对角线x 的取值范围是1025<≤x . (3)由(1)(2)知，当25=x 时，矩形的面积最大，最大面积为25. 12答案:解析:(1)当x =5时，y =195；当x =25时，y =205.∴讲课开始后第25分钟时学生的注意力比讲课开始后第5分钟时更集中.(2)当0<t ≤10时，y =－t 2+24t +100=－(t －12)2+244，该图象的对称轴为t =12，在对称轴左侧，y 随t 的增大而增大，∴当t =10时,y 有最大值240.当20<t ≤40时,y =－7t +380.y 随t 的增大而减小, ∴当t =20时,y 有最大值240.∴讲课开始后10分钟时,学生的注意力最集中,能持续10分钟. (3)当0<t ≤10时，令y =－t 2+24t +100=180 ∴t =4；当20<t ≤40时,令y =－7t +380=180, ∴t ≈28.57. ∴学生注意力在180以上的时间可持续为28.57－4=24.57(分钟).∴老师可以经过适当安排,在学生注意力达到所需的状态下讲解完这道题目.。

20.1 二次函数基础能力训练★回归教材 注重基础 ◆二次函数的概念1.已知y=(m 2－1)x m2－m是二次函数,则m=_______. 2.下列函数表达式中不是二次函数的是( )A.y=3(x －1)2－1 B.22x y = C.52-=x y D.y=(x+1)(x －2)◆列二次函数的表达式3.(·福州)已知抛物线y=x 2－x －1与x 轴的一个交点为(m,0),则代数式m 2－m+2 008的值为( )A.2 006B.2 007C.2 008D.2 0094.某品牌的空调原价6 000元,如果每年的降价率为x,则两年后这种空调的价位为y 元,那么y 与x 之间的函数关系表达式为( )A.y=6000(1－x)2B.y=6 000(1－x)C.y=6000－x 2D.y=6 000(1+x)25.一个小球由静止开始在一个斜坡上向下滚动,通过仪器观察到小球滚动的距离s(米)与滚则s(米)与t(秒)之间的关系表达式为( )A.y=2tB.y=2t 2+2C.y=2t 2D.y=2(t －1)26.有一个长方体木块,其长和宽相等,高比长多2米.(1)若长方体的长和宽用x(米)表示,则长方体的表面积S(米2)如何表示?(2)如果将长方体的表面涂上油漆,每平方米所需要的费用是5元,那么给每个长方体涂漆的费用用y 元表示,则y 的表达式是什么?(3)如果长方体的长是1米,那么给10个这样的长方体涂漆需要多少费用?7.已知函数k kx x k k y -+++=2)(22.(1)当k 取何值时是二次函数? (2)当k 取何值时是一次函数?综合创新训练★登高望远 课外拓展 ◆创新应用8.银行的储蓄利率是随时间的变化而变化的,也就是说,利率是一个变量.在我国,利率的调整是中国人民银行根据国民经济发展的情况而决定的,设人民币一年定期储蓄的年利率是x,一年到期后.银行将本金和利息自动按一年定期储蓄转存,如果存款额是l 000元,那么请你写出两年后的本息和y(元)的表达式(不考虑利息税).若考虑利息税(利息税是利息的20％)呢?9.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多的利润,商店决定提高销售价格,经试验发现,若按每件20元的价格销售时,每月能卖360件,按每件25元销售时,每月能卖210件,假定每月销售的数量y(件)是价格x(元/件)的一次函数. (1)试求y 与x 的函数关系式；(2)如果以每件x 元销售时,每月可获利润为w 元,试写出w 与x 之间的关系式.它是x 的二次函数吗?◆开放探索10.如图20－1－1所示,等腰Rt△ABC 以2米/秒的速度沿直线l 向正方形移动,直到AB 与CD 重合.设x 秒时,三角形与正方形重叠部分的面积为y 米2. (1)写出y 与x 的函数关系表达式.(2)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?11.(·湖州)对于二次函数y=ax 2+bx+c,如果当x 取任意整数时,函数值y 都是整数,那么我们把该函数的图象叫做整点抛物线(例如：y=x 2+x+2).(1)请你写出一个二次项系数的绝对值小于1的整点抛物线的解析式(不必证明)； (2)请探索：是否存在二次项系数的绝对值小于21的整点抛物线?若存在,请写出其中一条抛物线的解析式；若不存在,请说明理由.参考答案1答案：2 解析：因为是二次函数，所以m 2－m=2，解得m 1=－1，m 2=2.但当m=－1时，二次项系数m 2－1=0，故舍去，只取m=2. 2答案：C3答案：D 解析：把(m ，0)代人y=x 2－x －1得：m 2－m －1=0，所以m 2－m=1，所以m 2－m+=1+=.4答案：A 解析：因为y=6000(1－x)×(1－x)=6000(1－x)25答案：C 解析：可将表格中数据代人四个选择支试试，也可从表格t 与s 的数量关系中总结出其所具有的特征.6答案：(1)S=6x 2+8x (2)y=30x 2+40x (3)700元解析：对于(1)S=x 2+x 2+x(x+2)×4=6x 2+8x ；对于(2)y=(6x 2+8x)×5=30x 2+40x ； 对于(3)(30×1+40×1)×10=700(元).7答案：解析：(1)由二次函数的定义可知k 2+k ≠0，解得k ≠0且k ≠－1.(2)若为一次函数，则k 2+k=0，解得k 1=0,k 2=－1，但当k=0时，原式变为2y 显然不是一次函数，所以舍去，只取k=－1.8答案：y=1 000x 2+2 000x+1 000(不考虑利息税)y=640x 2+1 600x+1 000(考虑利息税)解析：对于第一种情况：y=1 000(1+x)×(1+x)=1 000(1+x)2整理即得答案； 对于第二种情况，y=1 000x ·(1－20％)+1 000+[1 000x ·(1－20％)+1 000]·x ·(1－20％)，整理得y=640x 2+1 600x+1 000.9答案：解析：(1)设y 与x 的关系式为y=kx+b.由题意知，x=20，y=360和x=25，y=210符合上述关系式，故⎩⎨⎧+=+=,25210,20360b k b k 有解得k=－30，b=960， ∴y 与x 的函数关系式为y=－30x+960. (2)设每月的销售利润为w ，则w=y·(x－16)=(－30x+960)(x －16)w=－30x 2+1440x －15 360. 显然，w 是x 的二次函数.10答案：解析：对于(1)设经过x 秒后的图形如图所示：则CC ′=2x ，△C'CE ∽△C'BA ，所以B C''CC AB CE =,即424x CE =，解得CE=2x ， 所以，y=21CC ′·CE=21·2x ·2x=2x 2. (2)由题意知84421=⨯⨯=y ，即8=2x 2，解得x=±2 (舍负)，取x=2(秒).11答案：解析：(1)如：x x y 21212+=，x x y 21212-=－等等(只要写出一个符合条件的函数解析式即可)(2)假设存在符合条件的抛物线，则对于抛物线y=ax 2+bx+c ，当x=0时，y=c ；当x=1时，y=a+b+c.由整点抛物线定义可知：c 为整数，a+b+c 为整数，所以a+b 必为整数，又当x=2时，y=4a+2b+c=2a+2(a+b)+c 是整数，所以2a 必为整数，从而a 应为21的整数倍，因为a ≠0，所以21||≥a ,所以不存在二次项系数的绝对值小于21的整点抛物线.英语不规则动词归类记忆表原形 过去式 过去分词 汉语意思 read read read 读cut cut cut 切，割 let let let 让 put put put 放cost cost cost 花费，值 hit hit hit 撞，击 setsetset安排，安置三、ABC型四、ABB型不规则单词测试卷（1）微信添加“小魔方站”或“fifteen1617”免费获得更多中考资料与模拟试题不规则单词测试卷（2）不规则单词测试卷（3）不规则单词测试卷（4）。

反比例函数的概念课后作业1. 函数y=（m 2-m ）132+-m m x 是反比例函数，则（ ）A ．m≠0B ．m≠0且m≠1C ．m=2D ．m=1或22. 定义：[a ，b]为反比例函数y ＝bxa （ab≠0，a ，b 为实数）的“关联数”． 反比例函数y ＝x k 1的“关联数”为[m ，m+2]，反比例函数y ＝x k 2的“关联数”为[m+1，m+3]，若m ＞0，则（ ） A ．k 1=k 2 B ．k 1＞k 2 C ．k 1＜k 2 D ．无法比较3. 设某矩形的面积为S ，相邻的两条边长分别为x 和y ．那么当S 一定时，给出以下四个结论： ①x 是y 的正比例函数；②y 是x 的正比例函数；③x 是y 的反比例函数；④y 是x 的反比例函数其中正确的为（ ）A ．①，②B ．②，③C ．③，④D ．①，④4. 计划修建铁路lkm ，铺轨天数为t （d ），每日铺轨量s （km/d ），则在下列三个结论中，正确的是（ ）①当l 一定时，t 是s 的反比例函数；②当l 一定时，l 是s 的反比例函数；③当s 一定时，l 是t 的反比例函数．A ．仅①B ．仅②C ．仅③D ．①，②，③5. 给出的六个关系式：①x （y+1）②y ＝22+x ③y ＝④y ＝−x 21⑤y ＝2x ⑥y ＝x 32；其中y 是x 的反比例函数是（ ）A ．①②③④⑥B ．③⑤⑥C ．①②④D ．④⑥6. 已知函数y ＝(k −2) 52-k x，当k= 时，y 是x 为反比例函数． 7. 函数y=m x m 1-是反比例函数，则m= ．8. 将x=32代入反比例函数y=-x1中，所得函数值记为y 1，又将x=y 1+1代入原反比例函数中，所得函数值记为y 2，再将x=y 2+1代入原反比例函数中，所得函数值记为y 3，…，如此继续下去，则y 2015= ．9. 如果函数y=（n-4）352+-n n x 是反比例函数，那么n 的值为 ．10. 已知函数y=（m+1）x|2m|-1，①当m何值时，y是x的正比例函数？②当m何值时，y是x的反比例函数？（上述两个问均要求写出解析式）11. 已知函数y=2y1-y2，y1与x+1成正比例，y2与x成反比例，当x=1时，y=4，当x=2时，y=3，求y与x的函数关系式．12. 写出下列函数关系式，并指出其中的反比例函数及正比例函数．（1）当圆柱的体积是50cm3时，他的高h（cm）与底面圆的面积S（cm2）的关系；（2）玲玲用200元钱全部用来买营养品送给她妈妈，那么她所能购买营养品的数量y（kg）与单价x（元/kg）的关系．反比例函数的概念课后作业参考答案1. 解析：依据反比例函数的定义求解即可．解：由题意知：m 2-3m+1=-1，整理得 m 2-3m+2=0，解得m 1=1，m 2=2．当m=l 时，m 2-m=0，不合题意，应舍去．∴m 的值为2．故选C2. 解析：利用题中的新定义表示出k 1与k 2，利用作差法比较即可．解：根据题意得：k 1＝2+m m ，k 2＝31++m m ， ∵m ＞0，∴k 1-k 2=2+m m -31++m m =)3)(2(23322++---+m m m m m m =-)3)(2(2++m m ＜0， 则k 1＜k3. 解析：此题可先根据题意列出函数关系式，再根据反比例函数的定义进行判断．解：设某矩形的面积为S ，相邻的两条边长分别为x 和y ．那么当S 一定时，x 与y 的函数关系式是y=xs ， 由于S≠0，且是常数，因而这个函数是一y 是x 的反比例函数．同理x 是y 的反比例函数．正确的是：③，④．故选C4. 解析：根据工作总量=工作效率×时间，整理为反比例函数的一般形式：y ＝x k （k≠0），根据k 是常数，y 是x 的反比例函数判断正确选项即可．解：∵l=ts ，∴t=s I 或s=tI ， ∵反比例函数解析式的一般形式y ＝x k （k≠0，k 为常数）， ∴当l 一定时，t 是s 的反比例函数；只有①正确，故选A ．5. 解析：根据反比例函数的一般形式是y ＝xk （k≠0），可得答案． 解：①x （y+1）是整式的乘法，②不是反比例函数；③不是反比例函数，④是反比例函数，⑤是正比例函数，⑥是反比例函数，故选：D ．6. 解析：根据y=kx -1（k≠0）是反比例函数，可得答案．解：由函数y ＝(k −2)xk 2−5是反比例函数， k 2-5=-1，且k-2≠0，解得k=-2．故答案为：-27. 解析：由反比例函数的定义可知|m|=1，且m-1≠0，从而可求得m 的值解：∵y=m x m 1-是反比例函数，∴|m|=1，且m-1≠0．解得：m=-1．故答案为：-1．8. 解析：根据数量关系分别求出y 1，y 2，y 3，y 4，…，不难发现，每3次计算为一个循环组依次循环，用2014除以3，根据商和余数的情况确定y 2015的值即可．解：∵y 1=-23，y 2=-1231+=2，y 3=-211+=-31，y 4=-1311+-=-23，…， ∴每3次计算为一个循环组依次循环，∵2015÷3=671余2，∴y 2015为第672循环组的第2次计算，与y 2的值相同，故答案为：29. 解析：根据反比例函数的一般形式，即可得到n 2-5n+3=-1且n-4≠0，即可求得n 的值． 解：根据题意得：n 2-5n+3=-1且n-4≠0，解得：n=1，故答案是：110. 解析：①根据正比例函数的定义得到|2m|-1=1，且m+1≠0；②根据正比例函数的定义得到|2m|-1=-1，且m+1≠0；解：①∵函数y=（m+1）x |2m|-1是正比例函数，∴|2m|-1=1，且m+1≠0，解得，m=1；即当m=1时，y 是x 的正比例函数；②∵函数y=（m+1）x |2m|-1是反比例函数，∴|2m|-1=-1，且m+1≠0，解得，m=0；即当m=0时，y 是x 的反比例函数11. 解析：根据正比例函数和反比例函数的定义得到y 1，y 2的关系式，进而得到y 的关系式，把所给两组解代入即可得到相应的比例系数，也就求得了所求的关系式． 解：由题意得：y 1=k 1（x+1），y 2=xk 2 ∵y=2y 1-y 2， ∴y=2k 1（x+1）-xk 2 ∴4＝4k 1−k 2，3＝6k 1−22k ， 解得：k 1＝41 ，k 2＝−3， ∴y=21（x+1）-x3 ， 即y=21x+x 3+21 12. 解析：（1）根据圆柱体积公式列出函数式，根据函数式判定函数类型；（2）根据总价=数量×单价列出函数式，根据函数式确定函数类型． 解：（1）依题意得 50=Sh ．S=h50该函数是S 关于h 的反比例函数； （2）依题意得 y=x 200该函数是y 关于x 的反比例函数。