下载文档原格式
插补原理：在实际加工中，被加工工件轮廓形状千差万别，严格说来，为了满足几何尺寸精度要求，刀具中心轨迹应该准确地依照工件轮廓形状来生成，对于简单曲线数控系统可以比较容易实现，但对于较复杂形状，若直接生成会使算法变得很复杂，计算机工作量也相应地大大增加，因此，实际应用中，常采用一小段直线或圆弧去进行拟合就可满足精度要求(也有需要抛物线和高次曲线拟合情况)，这种拟合方法就是“插补”，实质上插补就是数据密化过程。
插补任务是根据进给速度要求，在轮廓起点和终点之间计算出若干个中间点坐标值，每个中间点计算所需时间直接影响系统控制速度，而插补中间点坐标值计算精度又影响到数控系统控制精度，因此，插补算法是整个数控系统控制核心。
插补算法经过几十年发展，不断成熟，种类很多。
一般说来，从产生数学模型来分，主要有直线插补、二次曲线插补等；从插补计算输出数值形式来分，主要有脉冲增量插补(也称为基准脉冲插补)和数据采样插补[26]。
脉冲增量插补和数据采样插补都有个自特点，本文根据应用场合不同分别开发出了脉冲增量插补和数据采样插补。
1数字积分插补是脉冲增量插补一种。
下面将首先阐述一下脉冲增量插补工作原理。
2.脉冲增量插补是行程标量插补，每次插补结束产生一个行程增量，以脉冲方式输出。
这种插补算法主要应用在开环数控系统中，在插补计算过程中不断向各坐标轴发出互相协调进给脉冲，驱动电机运动。
一个脉冲所产生坐标轴移动量叫做脉冲当量。
脉冲当量是脉冲分配基本单位，按机床设计加工精度选定，普通精度机床一般取脉冲当量为：0.01mm，较精密机床取1或0.5 。
采用脉冲增量插补算法数控系统，其坐标轴进给速度主要受插补程序运行时间限制，一般为1~3m/min。
脉冲增量插补主要有逐点比较法、数据积分插补法等。
逐点比较法最初称为区域判别法，或代数运算法，或醉步式近似法。
这种方法原理是：计算机在控制加工过程中，能逐点地计算和判别加工偏差，以控制坐标进给，按规定图形加工出所需要工件，用步进电机或电液脉冲马达拖动机床，其进给方式是步进式，插补器控制机床。
数据采样插补一、概述数据采样插补多用于进给速度要求较高的闭环掌握系统。
它与前面我们介绍的插补方法的最大不同就是前者计算机一般不包含在伺服掌握环内，计算机插补的结果是输出进给脉冲，伺服系统依据进给脉冲进给。
每进给一步（一个脉冲当量），计算机都要进行一次插补运算。
进给速度受计算机插补速度的限制，很难满意现代数控机床高速度的要求。
而后者计算机一般包含在伺服掌握环内。
数据采样插补用小段直线来靠近给定轨迹，插补输出的是下一个插补周期内各轴要运动的距离，不需要每走一个脉冲当量就插补一次，可达到很高的进给速度。
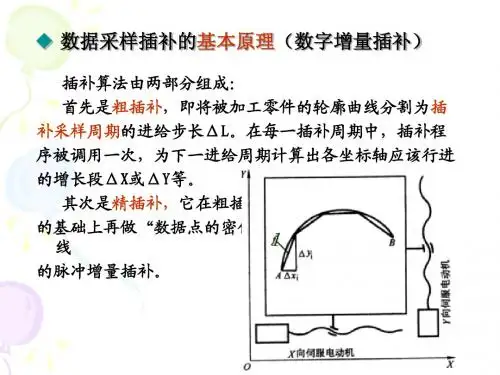
1. 数据采样插补的基本原理粗插补：采纳时间分割思想，依据进给速度F和插补周期T，将廓型曲线分割成一段段的轮廓步长L，L=FT，然后计算出每个插补周期的坐标增量。
精插补：依据位置反馈采样周期的大小，由伺服系统的硬件完成。
2. 插补周期和检测采样周期插补周期大于插补运算时间与完成其它实时任务时间之和，现代数控系统一般为2~4ms，有的已达到零点几毫秒。
插补周期应是位置反馈检测采样周期的整数倍。
3.插补精度分析直线插补时，轮廓步长L与被加工直线重合，没有插补误差。
圆弧插补时，轮廓步长L作为弦线或割线对圆弧进行靠近，存在半径误差。
二、数据采样法直线插补1.插补计算过程（1）插补预备主要是计算轮廓步长l＝FT及其相应的坐标增量。
（2）插补计算实时计算出各插补周期中的插补点（动点）坐标值。
2.有用的插补算法（1）直线函数法插补预备：插补计算：2）进给速率数法（扩展DDA法）插补预备: 引入步长系数K则插补计算：三、数据采样法圆弧插补1. 直线函数法（弦线法）如图5-13所示，要加工圆心在原点O（0，0）、半径为R的第一象限顺圆弧，在顺圆弧上的B点是继A点之后的插补瞬时点，两点的坐标分别为A（Xi，Yi）、B（Xi＋1，Yi＋1），现求在一个插补周期T内X 轴和Y轴的进给量△X、△Y。
图中的弦AB是圆弧插补时每个插补周期内的进给步长l，AP是A点的圆弧切线，M是弦的中点。
运动控制插补原理及实现数控系统加工的零件轮廓或运动轨迹一般由直线、圆弧组成，对于一些非圆曲线轮廓则用直线或圆弧去逼近。
插补计算就是数控系统根据输入的基本数据，通过计算，将工件的轮廓或运动轨迹描述出来，边计算边根据计算结果向各坐标发出进给指令。
数控系统常用的插补计算方法有：逐点比较法、数字积分法、时间分割法、样条插补法等。
逐点比较法，即每一步都要和给定轨迹上的坐标值进行比较，视该点在给定规矩的上方或下方，或在给定轨迹的里面或外面，从而决定下一步的进给方向，使之趋近给定轨迹。
直线插补原理图3—1是逐点比较法直线插补程序框图。
图中n是插补循环数，L是第n个插补循环中偏差函数的值，Xe，Y。
是直线的终点坐标，m是完成直线插补加工刀具沿X，y轴应走的总步数。
插补前，刀具位于直线的起点，即坐标原点，偏差为零，循环数也为零。
在每一个插补循环的开始，插补器先进入“等待”状态。
插补时钟发出一个脉冲后，插补器结束等待状态，向下运动。
这时每发一个脉冲，触发插补器进行一个插补循环。
所以可用插补时钟控制插补速度，同时也可以控制刀具的进给速度。
插补器结束“等待”状态后，先进行偏差判别。
若偏差值大于等于零，刀具的进给方向应为+x，进给后偏差值成为Fm-ye；若偏差值小于零，刀具的进给方向应为+y，进给后的插补值为Fm+xe。
进行了一个插补循环后，插补循环数n应增加l。
最终进行终点判别，若n<m，说明直线插补没有完毕，应继续进行插补；否则，表明直线加工完毕，应结束插补工作。
由上面的插补计算可知，每走一步，都要进行一下4个步骤(也称节拍)的算术运算或逻辑判断，其工作循环为：方向判定：根据插补值判定进给方向。
坐标进给：由判定方向向该坐标方向发一个进给脉冲。
偏差计算：每走一步到达新坐标点，按偏差公式计算新的偏差。
终点判别：若到达终点就结束插补计算；若未到达就重复上述循环步骤。
数控加工中两种插补原理及对应算法数控机床上进行加工的各种工件，大部分由直线和圆弧构成。
因此，大多数数控装置都具有直线和圆弧的插补功能。
对于非圆弧曲线轮廓轨迹，可以用微小的直线段或圆弧段来拟合。
插补的任务就是要按照进给速度的要求，在轮廓起点和终点之间计算出若干中间控制点的坐标值。
由于每个中间点计算的时间直接影响数控装置的控制速度，而插补中间点的计算精度又影响整个数控系统的精度，所以插补算法对整个数控系统的性能至关重要，也就是说数控装置控制软件的核心是插补。
插补的方法和原理很多，根据数控系统输出到伺服驱动装置的信号的不同，插补方法可归纳为脉冲增量插补和数据采样插补两种类型。
一、脉冲增量插补这类插补算法是以脉冲形式输出，每次插补运算一次，最多给每一轴一个进给脉冲。
把每次插补运算产生的指令脉冲输出到伺服系统，以驱动工作台运动。
一个脉冲产生的进给轴移动量叫脉冲当量，用δ表示。
脉冲当量是脉冲分配计算的基本单位，根据加工的精度选择，普通机床取δ＝0.01mm，较为精密的机床取δ＝1μm或0.1μm。
插补误差不得大于一个脉冲当量。
这种方法控制精度和进给速度低，主要运用于以步进电动机为驱动装置的开环控制系统中。
二、数据采样插补数据采样插补又称时间标量插补或数字增量插补。
这类插补算法的特点是数控装置产生的不是单个脉冲，而是数字量。
插补运算分两步完成。
第一步为粗插补，它是在给定起点和终点的曲线之间插入若干个点，即用若干条微小直线段来拟合给定曲线，每一微小直线段的长度△L都相等，且与给定进给速度有关。
粗插补时每一微小直线段的长度△L与进给速度F和插补T周期有关，即△L＝FT。
