当前位置：文档之家 › 5-线弹性断裂力学3-小范围屈服

5-线弹性断裂力学3-小范围屈服

  • 格式：ppt
  • 大小：415.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

断裂力学-线弹性理论(共53张PPT)

断裂力学-线弹性理论(共53张PPT)

断裂动力学
● 1948年N．F．Mott(莫特), 进行了裂纹快速扩展速度的定量计算并将动能引入Griffith能量准 那么;
● 1951年，E．H．Yoffe(约飞) ,提出了恒长度裂纹的匀速扩展模型，计及惯性力，对 裂纹分叉作定量分析;
1960年，J．W．Craggs(克拉格斯) ,提出了裂纹面受载而加载点随裂纹前进的匀速扩展半 无限长裂纹模型；
K反映了裂尖应力场的强弱；足标1表示是1型。
sij越大，K越大；裂纹尺寸a越大，K越大。 K的量纲为[应力][长度]1/2，常用MPa m。
(5-1)式是中心穿透裂纹无穷大板的解。 断裂力学研究表明，K1可以更一般地写为：
K1 s a f (a,W,...)
f(a,W,...)为几何修正函数，可查手册。 特别地，当a<<w或a/w0时，即
这种连续介质模型仍是一种理想的模型，在远离 裂纹尖端的区域是适宜的，而在裂纹尖端附近的 小区域(原子或晶体结构的尺度范围)是否适宜， 还需深入到微观领域，弄清微观的断裂机理，才 能更好地了解力学因素在裂纹尖端的断裂过程中 是如何发挥作用的，才能深入了解宏观断裂的现
二、断裂力学中的几个根本概念
● Griffth(格里菲斯)裂纹
●1960年，D．S.Dugdale (达格代尔) 研究裂纹尖端的塑性区。
●1961年，A．A．Wells(威尔斯)提出的裂纹张开位移(COD)准那么。
●1968年,J.R．Rice(赖斯)提出用围绕裂纹尖端的与路径无关的线积分来研究裂纹尖 端的变形及J积分准那么。
●1968年，J．W．Hutchinson(哈钦森)及J．R．Rice与G．R．Rosengren
● 1977 Comninou(康尼诺)，和1988Delale(迪拉尔)和Erdogan，1989 Hutchinson ,和 Sun(锁志刚)提出的能量释放率扩展准那么；

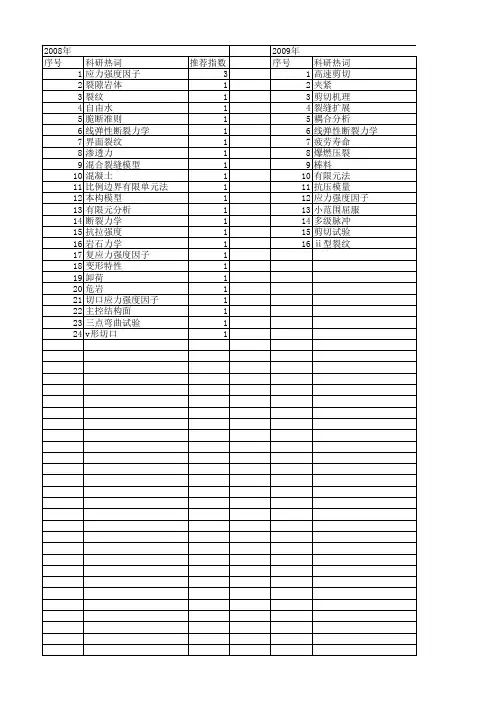
【国家自然科学基金】_线弹性断裂力学_基金支持热词逐年推荐_【万方软件创新助手】_20140802

【国家自然科学基金】_线弹性断裂力学_基金支持热词逐年推荐_【万方软件创新助手】_20140802

推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词 裂纹 隧道工程 陶瓷 锈胀力 钢筋混凝土 过程分析 裂缝扩展 裂纹张开位移 网格敏感性 结构分析 细观脆断模型 等效断裂准则 渗流-损伤-应力耦合 无砟轨道 断裂韧度 断裂力学 数值计算 损伤演化 损伤 复合材料 功能梯度材料 列车荷载 内水外渗
推荐指数 4 3 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3
2014年 科研热词 环境致裂 小裂纹 304不锈钢 推荐指数 1 1 1
推荐指数 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 高速剪切 夹紧 剪切机理 裂缝扩展 耦合分析 线弹性断裂力学 疲劳寿命 爆燃压裂 棒料 有限元法 抗压模量 应力强度因子 小范围屈服 多级脉冲 剪切试验 ⅱ型裂纹

07--小范围屈服与平面应变断裂韧度@@@@

07--小范围屈服与平面应变断裂韧度@@@@

在外加载荷作用下裂纹尖端的应力有限 有两种原因。其一是裂尖的材料会发生 不同程度的塑性变形，其二是裂纹尖端 并不是理想的曲率无穷大的形状，而总 是有钝化的。 如果裂纹尖端的塑性区（或者说偏离K场 的区域）很小，从而对裂纹尖端场的总 体影响不大，我们仍然可以认为是K场主 导着裂纹的行为。K仍然是裂纹扩展的主 导参数，只是对其进行适当的修正，这 种情况我们称为小范围屈服。
以上的分析是一种非常简化的分析，实际上裂纹尖端 的塑性区尺寸和形状与上面的结果都有所偏差。在平 面应力情况下，还有其他的塑性区形状，如窄条屈服 区。 在三维情况下，例如核电站的压力容器和管道中的一 个穿透裂纹，塑性区是一个三维的复杂形状。
考虑塑性修正后的K
在考虑塑性区修正后，裂纹前方的应力场变成了的 ABC 分布，也就是说在塑性区以外的应力场相等于向前移 动了（ R0 r0）的距离。因为 R0 2r0 ，所以Irwin建议将 裂纹尺寸进行如下的修正:
x2
A
22或 eff
A B B
ys
C
r0 R0
C
x1
a
如图所示，虚线 AC表示线弹性裂纹尖端 场即K场，曲线 ABC 表示考虑塑性区引 起应力松驰后的应力分布，其中近似认 为 BC 是 BC 段的简单平衡。在小范围屈 服条件下，认为 BC 下方的面积等于 BC 下方的面积。因此，要使裂纹前方延长 线上的应力与外载相平衡，就要求应力 22 松驰后的曲线 ABC 与线弹性的K场下面 AB 的面积相等，即：
K I KC
K与 之间的关系
根据能量释放率得到 了无限大板中的临界 应力 C 和临界裂纹长 度：
aC 2E
•根据K准则，也可以得 到(由 K a KIC ):

第七章弹塑性断裂力学简介详解

第七章弹塑性断裂力学简介详解

； xy =0
5
sx =s y =s
a 2r
=
K1
2p r
； xy =0
对于平面问题，还有： yz=zx=0；
sz=0 sz=(sx+sy)
则裂纹线上任一点的主应力为：
平面应力 平面应变
s1 =s 2 =
K1
2p r
；
s3=20 K1/
2p r
平面应力 平面应变
塑性力学中，von Mises屈服条件为：
sys
B A
假定材料为弹性-理想塑性，
D K
屈服区内应力恒为sys，应力分
o rp
x
布应由实线AB与虚线BK表示。 a
与原线弹性解(虚线HK) 相比较，少了HB部分大 于sys的应力。
8
TAhBeHs区im域pl表e a示na弹ly性sis材as料ab中o存ve在is
sy H
n的ot力st，ric但tl因y c为or应re力ct 不be能cau超se过it屈was
(s1 -s 2 )2 + (s 2 - s 3 )2 + (s 3- s1)2=2 sy2s
6
将各主应力代入Mises屈服条件，得到：
K1 / 2p rp = s ys (1- 2)K1/ 2prp = s ys
(平面应力) (平面应变)
故塑性屈服区尺寸rp为：
rp=
1 2p
(
sKy1s)2
rp = 21p(sKy1s)2(1-2)2
线弹性断裂力学给出的裂纹尖端附近的应力趋于 无穷大。然而，事实上任何实际工程材料，都不 可能承受无穷大的应力作用。因此，裂尖附近的 材料必然要进入塑性，发生屈服。
2

断裂力学知识点概要

断裂力学知识点概要
2 2 2θ 2θ r=（K I/2дσ S）cos 2 (1+3sin 2 )
7、 为保证线弹性断裂力学的精确性和有效性，裂纹尖部的区域应限制在如下的范围之内： Ry≤r≤a/10. 通常把应力水平（σ/σs）≤0.3~0.5 作为线弹性断裂力学的适用范围。 （σ/σs）≤0.53. 8、 裂纹失稳扩展的条件是裂纹体在裂纹扩展过程中所释放的应变能大于等于裂纹扩展时 形成新的裂纹表面所需要的表面能。这就是能量平衡理论建立的断裂判据，习惯上称为 能量判据。 9、 三大理论：最大周向应力理论、应变能密度因子理论、最大应变能释放率理论。 10、 压力容器中裂纹的应力强度银子 KI 的计算：KI=MK/I M——膨胀效应系数（下述中 C2 为 C2， ） C2 1/2 对球星容器中的穿透裂纹膨胀效应系数计算式：M=(1+1.93* ) Rt C2 1/2 对圆筒形容器中的轴向裂纹，膨胀效应系数计算式：M=(1+1.61* ) Rt C2 1/2 对圆筒形容器中的环向裂纹，膨胀效应系数计算式：M=(1+0.32* ) Rt C——穿透裂纹或当量穿透裂纹的半长 R——容器的半径 T——容器的壁厚 11、一圆筒形压力容器，设计压力 P=2.0MPa，内径 D=7500mm，壁厚 t=40mm，焊接系数 Ψ=1，材料为 16MnR, σs=350MPa，KIC=3250N/mm1.5，在筒体的膜应力区有两条穿透裂纹，
σө≈ σψ≈
pD 2*7500 = =187.5（MPa） 2t 2*40
pD 2*7500 = =93.75（MPa） 4t 4*40
轴向裂纹的鼓胀效应系数为：M=(1+1.61* 环向裂纹的鼓胀效应系数为：M=(1+0.321/2=1.0002 Rt C2 1/2 10*10 ) （1+0.32* ）1/2=1.0001 Rt 3600*40

线弹性断裂力学PPT教案

线弹性断裂力学PPT教案
取单位厚度的无限大平板，中央有长 为2a的 穿透裂 纹，承 受与裂 纹垂直 的均匀 拉伸应 力，如 图所示 。
对于薄板，为平面应力状态
三个应力分量为：
x
a 2r
cos 2
(1 sin
2
sin
3 2
)
y
a 2r
cos 2
(1 sin 2
sin
3 2
)
xy
a 2r
sin
2
cos 2
co s 3 2
G G (或 )
C
GC
脆性断裂准则
K KC
K C (或 )
平面应变断裂韧性
平面应力断裂韧性。
通常把K准则作为断裂准则的常用形 式，为 什么？
应用K准则，应力强度因子的数值一般由计算得出，断裂韧性 的数值由试验测定。
第25页/共65页
2.3.4 K断裂准则
2. K准则与G准则的关系
对于Ⅱ型裂纹 ，按照与Ⅰ型裂纹问题同样的思路， 有
第1页/共65页
2.3.1 裂纹体的三种断裂类型
裂纹体中的裂纹，由于外加作用力的 不同， 可以分 为三种 不同的 类型， 如图所 示，相 应地称 为Ⅰ、 Ⅱ、Ⅲ 型断裂 问题
由于Ⅰ型裂纹是最常见和最危险的，容 易引起 超低应 力脆断 ；近年 来对I型 裂纹的 研究也 最多， 实际裂 纹即使 是复合 型裂纹 ，也往 往把它 作为Ⅰ 型裂纹 来处理 ，这样 更安全 。
G GC
K KC
G
1 E
K
2
(平面应力)
GC
1 2 E
K2 C
(平面应变)
对于Ⅲ型裂纹，有
G GC
K KC
G
1 E

断裂力学试卷2010(可编辑修改word版)

断裂力学试卷2010(可编辑修改word版)

华中科技大学土木工程与力学学院《断裂力学》考试卷（半开卷）2010～2011 学年度第一学期成绩学号专业班级姓名一二三四五六合计分数一、填空题（每空 2 分，共16 分）1. 在断裂力学中，小范围屈服是指（），当（）时，可以采用线弹性断裂力学，且能保证其精确度和有效性；而当塑性区尺寸与裂纹尺寸同数量级时称为（），只能采用（）来处理。

2. 复合型裂纹扩展与单纯张开型裂纹扩展的主要不同之处是（）。

因此，复合型裂纹的研究，除了需要确定临界状态，建立断裂判据外，还要确定（）。

常用的复合型裂纹脆性断裂理论有（）和（）等。

二、简答题（24 分）1. 设有两条Ⅰ型裂纹，其中一条长为4a，另一条长为a。

如前者加载到，后者加载到2。

问它们裂纹尖端附近的应力场是否相同？应力强度因子是否相同？2. 设有无限大平板 I 型裂纹，受轴向拉应力作用，裂纹顶端附近的应力为：=a3cos (1+ sin sin yy2r 2 2 ) ，其中a 为裂纹尺寸。

2（1）求应力强度因子KI；（2）当=0 时，在裂纹顶端和距裂纹顶端很远处，yy各为多少？与题设条件有无矛盾？如何解释？三、试用叠加法求图示无穷大板裂纹尖端应力强度因子。

（15 分）mP2at2aD p 题五图б2б1题三图四、圆拄形容器有一纵向穿透裂纹。

容器的内径D=100㎜，壁厚t=5㎜，最大工作压力p max =48MPa，材料的断裂韧性KⅠC=37MPa ，试求临界裂纹长度ac。

（15 分）题四图五、如图所示的杆件，若b a ，而且在杆端的位移为，试求恒载荷及恒位移情形下的应变能释放率GI 及应力强度因子KI。

（15 分）六、物体内部有一圆盘状深埋裂纹，直径为2.5cm，这一直径比物体的其它尺寸小得多，若垂直于裂纹面的方向作用拉应力700MPa，材料的屈服极限为930MPa，试计算等效应力强度因子。

（15 分）。

《线弹性断裂力学》课件

《线弹性断裂力学》课件
02
它涉及到材料或结构的强度、韧 性和耐久性等方面的评估，对于 工程结构的安全性和可靠性至关 重要。
断裂力学的重要性
在工程领域中，许多结构如桥梁、高 层建筑、压力容器等都需要承受较大 的外力，因此断裂力学对于这些结构 的可靠性评估具有重要意义。
通过断裂力学的应用，可以预测结构 在各种载荷下的行为，从而采取相应 的措施来提高结构的强度、韧性和耐 久性。
意义。
裂纹扩展的驱动力
总结词
裂纹扩展的驱动力是指促使裂纹扩展的力或能量来源，是线弹性断裂力学中的重要研究内容。
详细描述
裂纹扩展的驱动力可以来自外部载荷、温度梯度、化学腐蚀等多种因素。这些驱动力会导致裂纹面上 的应力分布发生变化，从而促使裂纹扩展。研究裂纹扩展的驱动力有助于深入了解材料的断裂机制和 行为，为结构的安全性和可靠性设计提供理论支持。
总结词
弹性模量是描述材料抵抗弹性变形能力的物理量，是线弹性断裂力学中的重要参数。
详细描述
弹性模量是指材料在弹性范围内，抵抗变形的能力。它是衡量材料刚度的指标，表示材料在单位应变下所需的应 力。弹性模量越大，材料抵抗变形的能力越强。在工程应用中，了解材料的弹性模量对于预测结构的强度和稳定 性至关重要。
未来研究展望
发展更为精确的数值模拟方法
利用高性能计算机和先进的数值方法，模拟更为复杂的断裂行为，提 高预测精度。
深入研究复杂环境和服役条件下的断裂问题
针对高温、高压、腐蚀等复杂环境和服役条件下的材料和结构，深入 研究其断裂行为和失效机理。
跨学科合作与交流
加强与其他学科领域的合作与交流，如物理学、化学、生物学等，以 促进对材料断裂行为的深入理解。
有限元分析方法可以处理复杂 的几何形状、材料非均匀性和 多种物理场耦合等问题，具有 广泛的应用前景。

线弹性断裂力学..

线弹性断裂力学..

载荷
形状系数
a ij＝ Y f（ ij ） 2 r
几何因素 当r=0，出现 奇异性
裂纹尖端附近的应力应变场
a ij＝ Y f（ ij ） 2 r
即：r趋于0时，应力
σij
无穷大
裂纹尖端部位的 应力 无穷大
似乎说明，只要结构有裂纹，将不能承受载荷
裂纹尖端附近的应力应变场---典型的拉伸曲线
的表面裂纹。现有两个钢种可供选择，其中，
甲钢种的σ s=2100MPa，KIC=50MPa m ；
乙钢种的σ s=1700MPa，KIC=84MPa m 。
试分析应该选用哪一种钢种合适。
按常规强度理论，两个钢种的强度安全系数分别为： 甲钢：
按常规强度理论，显然甲钢种的强度储备大于乙钢种
从断裂力学角度分析 由应力强度因子可以推导出材料断裂时的临界应力
KI Y a
a ij＝ Y f（ ij ） 2 r
应力强度因子 －KI
• 描述裂纹尖端应力应变场参量 • 可以认为是描述裂纹扩展的推动力的量
强度理论 • 应力（推动力）

• 许用应力的确定 • 建立强度条件
应力强度因子－KI • 描述裂纹尖端应力应变场参量 • 可以认为是描述裂纹扩展的推动力的量
II型(滑移型)
III型(撕开型)
I型裂纹尖端附近的应力应变场 模型
• 弹性体
• 无限大平板
• 中心穿透裂纹 • 四周均匀拉伸
I型裂纹尖端附近的应力应变场
• 初始边界条件： （1）当y=0,-a<x<a时， y=0。 （2）当y=0,|x|>a时， y> 。 （3）当y=0,x时， y= 。
材料屈服准则

线弹性断裂力学概述

线弹性断裂力学概述

K IC Y c a
不难看出，在线弹性条件下
GIC K IC E
必须指出，K I 与 K IC 是两个不同的概念， 应力强度因子 K I 是由载荷及裂纹体的形状和 尺寸决定的量，是表示裂纹尖端应力场强度的一个参量，可以用弹性理论的方法进行计算； 而断裂韧度 K IC 是材料具有的一种机械性能，表示材料抵抗脆性断裂的能力，由试验测定。 材料的断裂韧度随试件厚度的增加而下降，如图 5-4 所示。这是因为薄板的裂纹尖端处 于平面应力状态，裂纹不易扩展，其断裂韧度值较高，一般用 K C 表示平面应力断裂韧度。 随着板厚的增加，裂纹尖端处于平面应变状态的部分增加，裂纹较易扩展，因而断裂韧度下 降。 当板的厚度增加到某一定值以后， 裂纹韧度降至最低值， 称为平面应变断裂韧度， 用 K IC 表示。图 5-5 反映了加载速度对 KⅠC 影响。
三、裂纹类型
在断裂力学中，按裂纹受力情况，将裂纹分为三种基本类型，如图 5-2 所示。分别称为 张开型（Ⅰ型） 、滑开型（Ⅱ型）和撕开型（Ⅲ型） 。各种裂纹的受力情况如下：Ⅰ型裂纹受 垂直于裂纹面的拉应力的作用；Ⅱ型裂纹受平行于裂纹面而垂直于裂纹前缘的剪应力的作 用；Ⅲ型裂纹受既平行于裂纹面又平行于裂纹前缘的剪应力的作用。 Ⅰ型裂纹上下表面相对张开；Ⅱ型裂纹上下表面沿 X 轴相对滑开；Ⅲ型裂纹上下表面沿 Z 轴相对滑开。
图 5-4
板厚对应力强度因子的影响
图 5-5 加载速度对 KⅠC 影响
三、 线弹性力学在小范围屈服时的应用
线弹性断裂力学是以理想的线弹性体为对象的，然而对于一般的金属材料来说，其裂纹 端部将不可避免地出现一个或大或小的塑性区， 由于塑性区引起应力松弛， 使得该处的应力 场发生变化，对于小范围屈服，将线弹性断裂力学的公式加以修正。 裂纹平面内的法向应力，先不考虑塑性区的影响，当 0 时

线弹性断裂力学资料

线弹性断裂力学资料

线弹性断裂力学1、概念：断裂力学：断裂力学是以变形体力学为基础，研究含缺陷（或者裂纹）材料和结构的抗断裂性能，以及在各种工作环境下裂纹的平衡、扩展、失稳及止裂规律的一门学科。

线弹性断裂力学：应用线弹性理论研究物体裂纹扩展规律和断裂准则。

2、材料缺陷实际构件存在的缺陷是多种多样的，可能是冶炼中产生的夹渣、气孔，加工中引起的刀痕、刻槽，焊接时产生的裂缝、未焊透、气孔、咬边、过烧、夹杂物，铸件中的缩孔、疏松，以及结构在不同环境中使用时产生的腐蚀裂纹和疲劳裂纹。

在断裂力学中，常把这些缺陷都简化为裂纹，并统称为“裂纹”。

3、裂纹的类型（1）、按照裂纹的几何特征分类(a)穿透裂纹：厚度方向贯穿的裂纹。

(b)表面裂纹：深度和长度皆在构件的表面，常简化为半椭圆裂纹。

(c)深埋裂纹：裂纹的三维尺寸都在构件内部，常简化为椭园裂纹。

（2）按照裂纹的受力和断裂特征分类(a)张开型：（Ⅰ型，opening mode，or tensile mode）特征：外加拉应力垂直于裂纹面，也垂直于裂纹扩展的前沿线。

在外力的作用下，裂纹沿原裂纹开裂方向扩展。

(b)滑开型：（Ⅱ型, sliding mode, or in-plane shear mode）特征：外加剪应力平行于裂纹面，但垂直于裂纹扩展的前沿线。

在外力的作用下，裂纹沿原裂纹开裂方向成一定角度扩展。

(c)撕开型：（Ⅲ型, tearing mode, or anti-plane shear mode）特征：外加剪应力平行于裂纹面，也平行于裂纹扩展的前沿线。

使裂纹面错开。

在外力的作用下，裂纹基本上沿原裂纹开裂方向扩展。

Ⅲ型是最简单的一种受力方式，分析起来较容易，又称反平面问题。

(d)混合型：( 或复合型，mixed mode )经常是拉应力与剪应力同时存在，实际问题多半是Ⅰ＋Ⅱ，Ⅰ＋Ⅲ，Ⅰ＋Ⅱ＋Ⅲ等，从安全的角度和方便出发，将混合型问题常做简化看成Ⅰ型处理。

（3）按裂纹形状分类根据裂纹的真实形状，一般可以分为圆型、椭圆型、表面半圆型、表面半椭圆型，以及贯穿直裂纹等。

第一章 线弹性断裂力学

第一章 线弹性断裂力学

第一章 线弹性断裂力学线弹性断裂力学认为，材料和构件在断裂以前基本上处于弹性范围内，可以把物体视为带有裂纹的弹性体。

研究裂纹扩展有两种观点：一种是能量平衡的观点，认为裂纹扩展的动力是构件在裂纹扩展中所释放出的弹性应变能，它补偿了产生新裂纹表面所消耗的能量，如Griffith 理论；一种是应力场强度的观点，认为裂纹扩展的临界状态是裂纹尖端的应力场强度达到材料的临界值，如Irwin 理论。

（李灏）§1.1 线弹性断裂力学的基本理论线弹性断裂力学的基本理论包括：Griffith 理论，即能量释放率理论；Irwin 理论，即应力强度因子理论。

一、Griffith 理论1913年，Inglis 研究了无限大板中含有一个穿透板厚的椭圆孔的问题，得到了弹性力学精确分析解，称之为Inglis 解。

1920年，Griffith 研究玻璃与陶瓷材料脆性断裂问题时，将Inglis 解中的短半轴趋于0，得到Griffith 裂纹。

Griffith 研究了如图1-1所示厚度为B 的薄平板。

上、下端受到均匀拉应力σ作用，将板拉长后，固定两端。

由Inglis 解得到由于裂纹存在而释放的弹性应变能为2222211U a BE U a BEνπσπσ-==平面应变平面应力图1-1其中：ν为泊松比。

另一方面，Griffith 认为，裂纹扩展形成新的表面，需要吸收的能量为4S a B γ=其中：γ为单位面积上的表面能。

如果应变能释放率d d U A ，等于形成新表面所需要吸收的能量率d d SA，则裂纹达到临界状态；如果应变能释放率d d U A 小于吸收的能量率d d SA，则裂纹稳定；如果应变能释放率d d U A 大于吸收的能量率d d SA，则裂纹不稳定。

因此可以得到如下表达式d()0d U S A -= 临界状态 d()0d U S A -< 裂纹稳定 d()0d U S A-> 裂纹不稳定 能量关系为()d dW U S dA dA-= (其中W 为外力功)板中初始的应变能20122U V V E σσε==,形成裂纹后系统的总能量012C U U U =-+.以平面应力为例：22242a U V a EE σπσγ=-+⇒2240U a a Eπσγ∂=-+=∂可得22c E a γπσ=，又22220U a E πσ∂=-<∂ 当22c E a γπσ=时，系统有极大内能。

断裂力学 弹塑性断裂力学

断裂力学 弹塑性断裂力学

和塑性区周围仍为广大的弹性区所包围。塑性区与弹性区 交界面上作用有均匀分布的屈服应力 s .
假想：挖去塑性区 在弹性区与塑性区的界面上加上均 匀拉应力 s 线弹性问题 裂纹尖端的应力强度因子
K Ic K I(1) K I( 2) c 2 s a c

c arccos
又
K I2 1 GI ' ' ( K IP K IF ) 2 E E
虚力Ｆ在裂纹尖端产生的应力强度因子
外力Ｐ在裂纹尖端产生的应力强度因子
10
U 0 1 U 2 lim lim[ ( K K ) ]da IP IF F F F E ' F 0 F 0 0 U K 2 lim( 0 ) lim ( K IP K IF ) IF da F F F 0 F 0 0 E '
4 K I ry v E 2 1 KI 2 ry ( ) 2 s
4 K I2 4GI 2v E s s
—小范围屈服时的COD计算公式
5
§4.2
D－B带状塑性区模型的COD
D－B模型假设：裂纹尖端的塑性区沿裂纹尖端两端延 伸呈尖劈带状。塑性区的材料为理想塑性状态，整个裂纹
弹塑性断裂力学
1
线弹性断裂力学 脆性材料或高强度钢所发生的脆性断裂 小范围屈服：塑性区的尺寸远小于裂纹尺寸 弹塑性断裂力学 大范围屈服:端部的塑性区尺寸接近或超过裂纹尺寸，
如：中低强度钢制成的构件． 全面屈服：材料处于全面屈服阶段，如：压力容器的 接管部位.
2
弹塑性断裂力学的任务：在大范围屈服下，确定能定 量描述裂纹尖端区域弹塑性应力，应变场强度的参量．以

第二章_线弹性断裂力学20100929

第二章_线弹性断裂力学20100929

dZ Z ( z + Δz ) − Z ( z ) 导数定义: Z ′( z ) = = lim dz Δz →0 Δz z = x + iy → Δz = Δx + iΔy
考虑路径： (1)Δx → 0, Δy = 0, Δz = Δx Re Z ( x + Δx, y) + i Im Z ( x+Δx, y) Re Z ( x, y) + i Im Z ( x, y) ′( z )= lim Z − lim Δy =0 Δy =0 Δx Δx Δx →0 Δx →0 Re Z ( x + Δx, y) − Re Z ( x, y) Im Z ( x+Δx, y) − Im Z ( x, y) = lim +i lim Δy =0 Δy =0 Δx Δx Δx →0 Δx →0
(z − a )
2 2 3 2
σ dZ dZ a 1 −3 Z ′( z ) = = =σ (− ξ 2 ) = − dz d ξ 2 2 2
Z ( z ) = ∫ Z ( z )dz = ∫
a − 3 − i 3θ r 2e 2 2
2 −i
σz
z 2 − a2
dξ = σ z − a → σ 2aξ = σ 2are
2
θ
2
KI θ θ 3θ cos (1 − sin sin ) 2 2 2 2π r KI θ θ 3θ σ y = Re Z + y Im Z ′ = cos (1 + sin sin ) 2 2 2 2π r KI θ θ 3θ τ xy = − y Re Z ′ = cos sin cos 2 2 2 2π r
积分 Z = ∫ ZdZ = Re Z + i Im Z Z = ∫ ZdZ = Re Z + i Im Z 它们都是解析函数，都满足柯西-黎曼条件

5-线弹性断裂力学3-小范围屈服(共19张)

5-线弹性断裂力学3-小范围屈服(共19张)
Irwin 研究了小范围屈服的情况，指出在该情况下
应力强度因子K 仍有意义。
第1页，共19页。
Irwin 小范围(fànwéi)屈服理论
第2页，共19页。
Irwin 小范围屈服(qūfú)理论
I 型裂纹尖端应力场为：
前面已指出，裂纹尖端应力场是渐进解，仅仅适合于裂纹尖端附近：
小范围屈服是指：
r rK 0.02a
Irwin 小范围屈服(qūfú)理论
将之代入Mises屈服方程中可得裂纹尖端塑性区边界线方程（平面应力）：
第5页，共19页。
Irwin 小范围(fànwéi)屈服理论
第6页，共19页。
Irwin 小范围(fànwéi)屈服理论
第7页，共19页。
Irwin 小范围屈服(qūfú)理论
为了揭示应力状态对裂纹尖端塑性尺寸的影响，Irwin引入了有效屈服应力和塑性约 束系数的概念。
第8页，共19页。
Irwin 小范围屈服(qūfú)理 论
将之代入Tresca屈服准则可得
第9页，共19页。
Irwin 小范围屈服(qūfú)理论
第10页，共19页。
理论
Irwin 小范围(fànwéi)屈服
第11页，共19页。
Irwin 小范围(fànwéi)屈服理论
• 现在，我们进一步考虑裂纹尖端塑性的影响。
但从物理学的角度来看真正奇异的应力是不可能的在裂纹尖端附近的材料必定发生屈irwin研究了小范围屈服的情况指出在该情况下应力强度因子k仍有意义
Irwin 小范围屈服(qūfú)理论
线弹性裂纹尖端场，其应力场具有 r -1/2 的奇异性， 该奇异性的幅值大小可用应力强度因子来表征。但从物
理学的角度来看，真正奇异的应力是不可能的，在裂纹 尖端附近的材料必定发生屈服。

6-线弹性断裂力学4-适用范围

6-线弹性断裂力学4-适用范围

a / W 0.45 ~ 0.55
平面应变断裂韧性KIC实验
• 试件加工中预验试件尺寸有何要求 （指裂纹长度a、韧带尺寸W-a及厚度B）？ 平面应变断裂韧性KIC实验试件加工时预制裂纹 长度满足什么要求？为什么？
平面应变断裂韧性KIC实验
• 根据平面应变断裂韧性KIC实验对试件尺寸的要求，国家已经制定了 标准：
平面应变断裂韧性KIC实验
平面应变断裂韧性KIC实验
平面应变断裂韧性KIC实验
平面应变断裂韧性KIC实验
• 可以看出，宽度W和厚度B有着一定的比例，裂纹长度a与W的比值限 制在一定的范围内：
(r a)
(r / a 0.02)
• 于是，K主导区域可表示为：
R r RK 0.02a
由于（考虑应力松弛影响后的经验公式）
可得
（保证裂尖有足够大的K主导区 和 “小范围屈服”条件 ）
为了保证“小范围屈服”和平面应变条件，还必须：
B 2.5(
K Ic
s
)2
式中B式试件厚度，W－a称为韧带尺寸。 • 平面应变断裂韧性KIC实验对试件尺寸的要求
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

KI = 2πr
KI = σ ys 2π ( R ry )
Irwin 小范围屈服理论
可得
ry = r0 =
1 R 2
Irwin 小范围屈服理论
Irwin 小范围屈服理论
思考题
Irwin 小范围屈服理论
以主应力表示的Mises屈服准则为
I 型裂纹尖端应力场为：
Irwin 小范围屈服理论
将之代入Mises屈服方程中可得裂纹尖端塑性区边界线方程（平面应力）： Mises
Irwin 小范围屈服理论
Irwin 小范围屈服理尖端塑性尺寸的影响，Irwin引入了有效屈 有效屈 服应力和塑性约束系数 塑性约束系数的概念。 服应力 塑性约束系数
Irwin 小范围屈服理论
将之代入Tresca屈服准则可得
Irwin 小范围屈服理论
Irwin 小范围屈服理论
Irwin 小范围屈服理论
现在，我们进一步考虑裂纹尖端塑性的影响。
Irwin 小范围屈服理论
Irwin 小范围屈服理论
Irwin 小范围屈服理论
σ y (r ) θ =0 =
Irwin 小范围屈服理论
线弹性裂纹尖端场，其应力场具有 r -1/2 的奇 异性， 该奇异性的幅值大小可用应力强度因子 应力强度因子来 应力强度因子 表征。但从物理学 物理学的角度来看，真正奇异的应力 物理学 是不可能的，在裂纹尖端附近的材料必定发生屈 服。 Irwin 研究了小范围屈服的情况，指出在该情 况下应力强度因子K 仍有意义。
Irwin 小范围屈服理论
Irwin 小范围屈服理论
I 型裂纹尖端应力场为：
前面已指出，裂纹尖端应力场是渐进解 渐进解，仅仅适合于裂纹尖端附近： 渐进解 小范围屈服是指：
r rK = 0.02 a
rp rK
塑性区形状的估算： 作下列假定： （1）忽略裂纹尖端材料屈服后对塑性区外K场的影响； （2）材料为理想塑性，且遵循 Von-Mises 屈服条件。