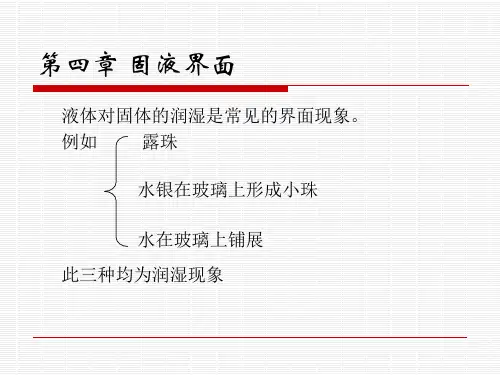
A 2 r r , A( s l g l g s ) 2 r r ( s l g l g s )
Vg h
2
Vg h
2
V 0, Ahm Ah 2 r rhm r 2 h 2 r r
粗糙因子(粗糙度):是固体的 真实表面积与相同体积固体假想 的平滑表面积之比。显然,r大 于等于1. r越大,表面越粗糙。
Wenzel方程的重要性是说明了表面粗糙化对接触角的 影响: • < 90°, ’< ,表面粗糙化使接触角变小,润湿性 更好。 • > 90°, ’> , 表面粗糙化会使润湿的体系更不 润湿。 • 揭示了均相粗糙表面的表观接触角与本征接触角之间 的关系 • 注意:Wenzel方程只适用于热力学稳定的平衡状态, 但由于表面不均匀,液体在表面上展开时需要克服一 系列由于起伏不平而造成的势垒。当液滴振动能小于 这种势垒时,液滴不能达到Wenzel方程所要求的平 衡状态而可能处于某种亚稳平衡状态。
180 ,Wa 0
90 , A 0
沾湿自发进行 浸湿自发进行 铺展自发进行
0 ,S 0
实用时,以90°为界:
若接触角大于90°,说明液体不能润湿固体, 如汞在玻璃表面; 若接触角小于90°,液体能润湿固体,如水 在洁净的玻璃表面。 若接触角等于0°或不存在平衡接触角时,说 明液体能铺展 渗透过程???
当固体表面由不同种类的化学物质组成时,如污染或多晶?? (2)Cassie模型 Cassie和Baxter进一步拓展了Wenzel的处理,提出 可以将粗糙不均匀的固体表面设想为一个复合表面,即认 为液滴在粗糙表面上的接触是一种复合接触。 设固体表面有物质1和2组成,这两种不同成分的表面是 以极小块的形式均匀分布在表面上的(每一小块的面积远 小于液滴的尺寸)。它们的本征接触角分别用1和 2表示, 在单位面积上所占的表面积分数分别为f1和f2(f1+f2=1)。 又设当液滴在表面展开时两种表面所占的分数不变。这时 可得到: