流体力学讲义——上海交通大学
- 格式:ppt
- 大小:3.58 MB
- 文档页数:41



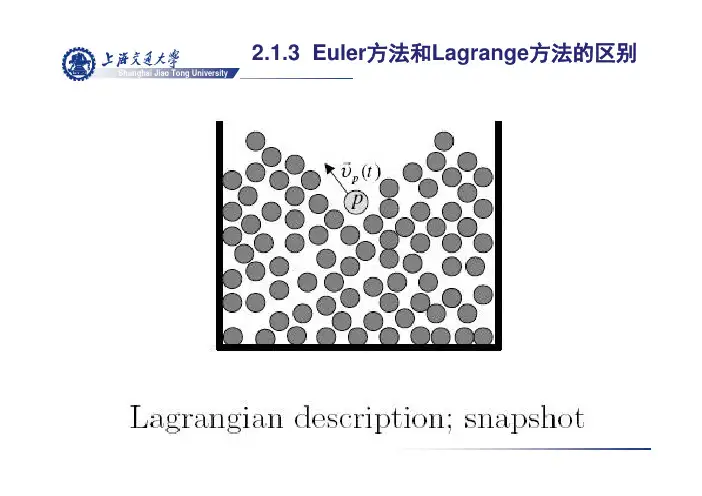
Shanghai Jiao Tong UniversityShanghai Jiao Tong UniversityShanghai Jiao Tong University 加速度:当地加速度(局部加速度)变位加速度(迁移加速度)'(, y ,,)(,,,)lim t ()x x y z z t t x y z t t u v w t x y zt +∆+∆+∆+∆-=∆→∆∂∂∂∂=+⋅+⋅+⋅∂∂∂∂∂=+⋅∇∂V V a V V V V V V V2.1.3Euler Shanghai Jiao Tong University2.1.3Euler方法和Lagrange方法的区别Shanghai Jiao Tong University注意:Euler方法中的空间点(x, y, z)与Lagrange方法中质点位置x, y, z有区别,Euler方法中的空间点(x, y, z)是t 的独立变量即与t无关,而Lagrange方法中质点位置x, y, z是t 的函数。
2.1.3Euler Shanghai Jiao Tong University2.2迹线和流线Shanghai Jiao Tong University上一节主要从数学上描述流体运动。
在本节,将讲述流体运动的几何表示。
Shanghai Jiao Tong University 2.2.1迹线定义:流体质点在连续时间内描绘出来的曲线,就是迹线(pathline)。
由于迹线是流体质点运动过程的路径,在Lagrange 法中,就是流体质点的位置函数:(,,,)(,,,)(,,,)x x a b c t y y a b c t z z a b c t =⎧⎪=⎨⎪=⎩2.2.1迹线Shanghai Jiao Tong University2.2.1迹线Shanghai Jiao Tong University2.2.1迹线Shanghai Jiao Tong UniversityShanghai Jiao Tong University一般情况给出的是u v wShanghai Jiao Tong University定义为参变量,积分时作常数处理。






Shanghai Jiao Tong University课程名称:船舶流体力学(NA235) Introduction to Marine Hydrodynamics 主讲人:万德成dcwan@辅导老师:林志良linzhiliang@张驰zhangchi0309@课程安排Shanghai Jiao Tong University课程性质:专业基础课学时数:68 =58 (理论课) +4 (实验实践)+ 6 (三次课程设计)成绩:作业和课程设计30%,期末考试70%Shanghai Jiao Tong University《水动力学基础》,刘岳元、冯铁城、刘应中编,上海交通大学出版社,1990《流体力学》,许维德,国防工业出版社,1989《流体力学》(上、下册),吴望一,北京大学出版社,1982《流体力学》(上、中、下册),丁祖荣,高等教育出版社,2003《流体力学基础》(上、下册),潘文全等,机械工业出版社,1982《流体力学》,易家训著(章克本、张涤明等),高等教育出版社,1983Shanghai Jiao Tong UniversityHydrodynamics, H. Lamb, 6th edition, CambridgeUniversity Press, 1932Marine Hydrodynamics, J.N. Newman, MIT Press, 1977An Introduction to Fluid Dynamics, G.R. Batchelor,Cambridge University Press, 1967Introduction to Fluid Mechanics,James A. Fay,MITPress, 1994Fundamentals of Fluid Mechanics,B.R. Munson, D.F.Young & T.H. Okiishi, Wiley Asia Student Edition, 2005 Fluid Mechanics: Fundamentals and Applications, Y.A.Cengel& J.M. Cimbala, McGraw-Hill, 2006Fluid Mechanics,5th Ed., F.M.White, McGraw-Hill.Shanghai Jiao Tong University第0章序论第0章序论Shanghai Jiao Tong University•流体力学与现实生活•流体力学的发展过程•流体力学的研究方法•流体力学的研究内容流体力学与现实生活Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 船舶工程船舶工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 船舶工程Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong University 船舶工程Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong University 船舶工程Shanghai Jiao Tong University螺旋浆船舶工程船舶工程Shanghai Jiao Tong University船舶工程Shanghai Jiao Tong University海洋工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 海洋工程航空航天Shanghai Jiao Tong University航空航天Shanghai Jiao Tong University航空航天Shanghai Jiao Tong University航空航天Shanghai Jiao Tong UniversityShanghai Jiao Tong University航空航天水利工程Shanghai Jiao Tong University水利工程Shanghai Jiao Tong UniversityShanghai Jiao Tong University 汽车阻力来自前部还是后部?汽车发明于19世纪末,当时人们认为汽车的阻力主要来自前部对空气的撞击,因此早期的汽车后部是陡峭的,称为箱型车,阻力系数C D 很大,约为0.8。