高一数学 暑假练习 正弦函数、余弦函数的图像与性质(3)
- 格式:doc
- 大小:229.00 KB
- 文档页数:2

2021年沪教版高一数学暑假作业:余弦函数的图像与性质【含答案】一、单选题1.下列命题中正确的是( ) A .cos y x =在第二象限是减函数 B .tan y x =在定义域内是增函数 C .|cos(2)|3y x π=+的周期是2π D .sin ||y x =是周期为2π的偶函数【答案】C【分析】根据函数的图象与图象变换进行判断.【详解】解:由余弦函数图象可知cos y x =在[]()2,2k k k Z πππ+∈上单调递减,故单调递减,但是在第二象限内不具有单调性,故A 错误;由正切函数的图象可知tan y x =在每一个周期内都是增函数,故tan y x =在定义域内不是增函数,故B 错误.cos(2)3y x π=+的周期为π,则|cos(2)|3y x π=+的图象是由cos(2)3y x π=+的图象将x 轴下方的部分翻折到x 轴上方得到的,故周期减半, |cos(2)|3y x π∴=+的周期是2π,故C 正确. sin ||y x =是偶函数,其图象是将sin y x =在y 轴右侧的函数图象翻折到y 轴左侧,所以函数sin ||y x =不是周期函数,故D 错误. 故选:C .2.若()y f x =的图像与cos y x =的图象关于x 轴对称,则()y f x =的解析式为( ) A .()cos y x =- B .cos y x =- C .cos y x = D .cos y x =【答案】B【分析】根据()f x -、()f x -、()fx 与()f x 的图象特征依次判断即可得到结果.【详解】对于A ,()cos cos y x x =-=,图象与cos y x =重合,A 错误; 对于B ,()y f x =与()y f x =-图象关于x 轴对称,cos y x ∴=-与cos y x =图象关于x 轴对称,B正确;对于C ,当0x ≥时,cos cos y x x ==,可知其图象不可能与cos y x =关于x 轴对称,C 错误; 对于D ,将cos y x =位于x 轴下方的图象翻折到x 轴上方,就可以得到cos y x =的图象,可知其图象与cos y x =的图象不关于x 轴对称,D 错误.故选:B.3.函数cos y x =在区间(),3ππ上的图像的对称轴是( ) A .3x π= B .52x π=C .2x π=D .x π=【答案】C【分析】根据余弦函数的性质即可求出对称轴.【详解】由余弦函数的性质可得函数cos y x =关于,x k k Z π=∈对称, 又(),3x ππ∈,则2x π=,故函数cos y x =在区间(),3ππ上的图像的对称轴是2x π=. 故选:C.4.若函数()3sin 12f x x ππ⎛⎫=-- ⎪⎝⎭,则()f x 是( ) A .周期为1的奇函数 B .周期为2的偶函数C .周期为1的非奇非偶函数D .周期为2的非奇非偶函数.【答案】B【分析】先化简()f x 的解析式可得()3cos 1f x x π=-,由正弦函数的周期公式和奇偶性的定义法可得答案.【详解】()3sin 13cos 12f x x x πππ⎛⎫=--=-⎪⎝⎭所以()f x 的最小正周期为22T ππ==又()()()3cos 13cos 1f x x x f x ππ-=--=-=,所以()f x 为偶函数. 故选:B二、填空题5.已知余弦函数过点,6m π⎛⎫-⎪⎝⎭,则m 的值为__________. 3【分析】将,6m π⎛⎫-⎪⎝⎭代入余弦函数即可求解. 【详解】设余弦函数为cos y x =, 由函数过点,6m π⎛⎫-⎪⎝⎭可得3cos 6m π⎛⎫=-= ⎪⎝⎭. 36.方程2cos 303⎛⎫++= ⎪⎝⎭x π的解集是____________. 【答案】22x x k ππ⎧=+⎨⎩或72,6x k k Z ππ⎫=-∈⎬⎭【分析】由题意可得出3cos 3x π⎛⎫+= ⎪⎝⎭,可得出3x π+的等式,由此可求得原方程的解集. 【详解】2cos 303x π⎛⎫+= ⎪⎝⎭,3cos 3x π⎛⎫∴+= ⎪⎝⎭ ()5236x k k Z πππ∴+=±∈,解得22x k ππ=+或()726x k k Z ππ=-∈,因此,方程2cos 303⎛⎫+= ⎪⎝⎭x π的解集是22x x k ππ⎧=+⎨⎩或72,6x k k Z ππ⎫=-∈⎬⎭. 故答案为:22x x k ππ⎧=+⎨⎩或72,6x k k Z ππ⎫=-∈⎬⎭. 【点睛】本题考查余弦方程的求解,考查计算能力,属于基础题. 7.函数2sin 3cos =+y x x 的值域为_____________. 【答案】[3,3]-【分析】设cos x t =,[]1,1t ∈-,得到231324y t ⎛⎫=--+⎪⎝⎭,根据二次函数性质得到值域.【详解】22sin 3cos 1cos 3cos y x x x x =+=-+,设cos x t =,[]1,1t ∈-,则223133124y t t t ⎛⎫=-++=--+ ⎪⎝⎭,函数在[]1,1t ∈-上单调递增,故1t =时,max 1313y =-++=,1t =-时,min 1313y =--+=-,故值域为[3,3]-. 故答案为:[3,3]-.【点睛】本题考查了三角函数的值域,意在考查学生的计算能力和转化能力,换元是解题的关键. 8.函数()lg cos f x x x =-在(,)-∞+∞内的零点个数为__________. 【答案】4【分析】在同一平面直角坐标系中作出函数|lg |y x =和cos y x =的图像如图, 结合图像的对称性可以看出两函数|lg |y x =和cos y x =的图像应有4个交点, 即函数()lg cos f x x x =-在(),-∞+∞内有4个零点, 故答案为:4.点睛:本题旨在考查化归转化的数学思想、函数方程思想、数形结合思想等数学思想的综合运用,求解时依据函数的对称性,先画出y 轴右边的函数的图像相交的情形,再根据对称性确定y 轴左边的函数的图像相交的情形,最终使得问题获解. 9.当3,44x ππ⎡⎤∈-⎢⎥⎣⎦时,函数()arcsin cos y x =的值域是______. 【答案】,42ππ⎡⎤-⎢⎥⎣⎦ 【分析】令cos t x =,3,44x ππ⎡⎤∈-⎢⎥⎣⎦,再利用反正弦函数的性质求解. 【详解】令cos t x =,3,44x ππ⎡⎤∈-⎢⎥⎣⎦,所以212t -≤≤, 因为arcsin y t =在2⎡⎤⎢⎥⎣⎦上递增, 所以arcsin 42t ππ-≤≤,所以函数()arcsin cos y x =的值域是,42ππ⎡⎤-⎢⎥⎣⎦. 故答案为:,42ππ⎡⎤-⎢⎥⎣⎦【点睛】本题主要考查反正弦函数的图象和性质,还考查了转化化归的思想和运算求解的能力,属于中档题.10.函数2()sin cos 2f x x x =+-的值域是________ 【答案】3[3,]4--【分析】化简得到2()cos cos 1f x x x =-+-,设cos x t =,得到21324y t ⎛⎫=--- ⎪⎝⎭,根据二次函数性质得到值域.【详解】22()sin cos 2cos cos 1f x x x x x =+-=-+-,设cos x t =,[]1,1t ∈-,则2213124y t t t ⎛⎫=-+-=--- ⎪⎝⎭, 当12t =时,函数有最大值为34-;当1t =-时,函数有最小值为3-.故函数值域为3[3,]4--. 故答案为:3[3,]4--.【点睛】本题考查了三角函数的值域,意在考查学生的计算能力和转化能力,换元转化为二次函数是解题的关键.11.方程2cos 210x -=的解集是___________. 【答案】{|6x x k ππ=+或,}6x k k Z ππ=-∈【分析】根据余弦函数的图象与性质解三角方程即可. 【详解】由2cos 210x -=可得:1cos 22x =, 所以223x k ππ=+或223x k ππ=-,()k ∈Z即6x k ππ=+或6x k ππ=-故答案为:{|6x x k ππ=+或,}6x k k Z ππ=-∈【点睛】本题主要考查了余弦函数的图象与性质,三角方程的解法,属于中档题. 三、解答题12.作出函数[]32cos ,,y x x ππ=-∈-的大致图象,并分别写出使0y >和0y <的x 的取值范围. 【答案】图象见解析;当,,66⎡⎫⎛⎤∈--⋃⎪ ⎢⎥⎣⎭⎝⎦x ππππ时,0y >;当,66x ππ⎛⎫∈- ⎪⎝⎭时,0y <. 【分析】利用五点作图法可得函数大致图象,令0y =,确定函数零点,数形结合得到所求x 的取值范围. 【详解】由五点作图法可知:x π-2π-2ππcos x1-0 11-y32+ 3 32- 3 32+由此可得函数大致图象如下图所示:令0y =32cos 0x =,3cos 2x ∴=,又[],x ππ∈-,6x π∴=-或6π,结合图象可知:当,,66⎡⎫⎛⎤∈--⋃⎪ ⎢⎥⎣⎭⎝⎦x ππππ时,0y >;当,66x ππ⎛⎫∈- ⎪⎝⎭时,0y <. 【点睛】本题考查五点作图法的应用、与余弦函数有关的不等式的求解;求解不等式可确定函数零点后,通过数形结合的方式来求解.13.利用“五点法”作出函数1cos y x =-,[]0,2x π∈的图像. 【分析】根据“五点法”的步骤先描点,再画出图象. 【详解】先找出五个关键点,列表如下:x2ππ32π 2π1cos y x =-0 121描点作出函数图象如下:14.求下列函数的单调递增区间: (1)3sin 24y x π⎛⎫=-⎪⎝⎭; (2)2cos 24y x π⎛⎫=+ ⎪⎝⎭; (3)sin y x =;(4)()22sin 2sin cos 3cos ,f x x x x x x R =++∈.【答案】(1)37,88k k ππππ⎡⎤++⎢⎥⎣⎦;(2)5,88k k ππππ⎡⎤-+-+⎢⎥⎣⎦;(3),2k k πππ⎡⎤+⎢⎥⎣⎦;(4)3,88k k ππππ⎡⎤-++⎢⎥⎣⎦.【分析】(1)利用诱导公式变形,由正弦型复合函数的单调性求解; (2)余弦型复合函数的单调性求解; (3)画出函数图象,结合函数图象即可判断;(4)首先利用二倍角公式及辅助角公式将函数化简,再根据正弦函数的性质计算可得.【详解】解:(1)2sin 22sin 244y x x ππ⎛⎫⎛⎫=-=-- ⎪ ⎪⎝⎭⎝⎭.由3222242k x k πππππ+-+,得3878k x k ππππ++,k Z ∈. 3sin 24y x π⎛⎫∴=- ⎪⎝⎭的单调增区间为37,88k k ππππ⎡⎤++⎢⎥⎣⎦,k Z ∈, (2)因为2cos 24y x π⎛⎫=+ ⎪⎝⎭由2224k x k ππππ-++,k Z ∈,得588k x k ππππ-+≤≤-+,k Z ∈. 2cos 24y x π⎛⎫∴=+ ⎪⎝⎭的单调增区间为5,88k k ππππ⎡⎤-+-+⎢⎥⎣⎦,k Z ∈, (3)sin y x =的图象是由sin y x =位于x 轴下方的图象关于x 轴翻折上去,函数图象如下所示:由函数图象可得函数的单调递增区间为,2k k πππ⎡⎤+⎢⎥⎣⎦,k Z ∈ (4)因为()22sin 2sin cos 3cos ,f x x x x x x R =++∈所以()sin 2cos 222224f x x x x π⎛⎫=++=++ ⎪⎝⎭令222,242k x k k Z πππππ-+≤+≤+∈,解得3,88k x k k Z ππππ-+≤≤+∈,故函数的单调递增区间为3,,88k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦15.如图,设A 、B 是半径为1的圆O 上的动点,且A 、B 分别在第一、二象限,C 是圆O 与x 轴正半轴的交点,△AOB 为等边三角形,记以Ox 轴正半轴为始边、射线OA 为终边的角为θ.(1)若点A 的坐标为34(,)55,求5sin()5cos()3cot()2πθπθθ--++-值;(2)设2()||f BC θ=,求函数()f θ的解析式和值域. 【答案】(1)3;(2)()22cos()3f πθθ=-+,值域为(2,23).【分析】(1)根据A 的坐标,利用三角函数的定义,求出sin θ,cos θ,再利用诱导公式,即可得到结论; (2)由题意,cos cos()3COB πθ∠=+,利用余弦定理,可得函数()f θ的解析式,从而可求函数的值域.【详解】解:(1)A 的坐标为34,55⎛⎫ ⎪⎝⎭,以Ox 轴正半轴为始边,射线OA 为终边的角为θ∴根据三角函数的定义可知,4sin 5θ=,3cos 5θ=,4tan 3θ=∴5sin()5cos()3cot()2πθπθθ--++-5sin 5cos 3tan θθθ=-++4345533553=-⨯+⨯+⨯=;(2))AOB 为正三角形,3AOB π∴∠=.cos cos()3COB πθ∴∠=+222()||||||2||||cos 22cos 3f BC OC OB OC OB COB πθθ⎛⎫∴==+-∠=-+ ⎪⎝⎭62ππθ<<, 5236πππθ∴<+<, 3cos 03πθ⎛⎫<+< ⎪⎝⎭,所以222cos 233πθ⎛⎫<-+< ⎪⎝⎭(2()2,3f θ∴+∈.【点睛】本题考查任意角的三角函数的定义,考查余弦定理求边长的平方,考查学生的计算能力,属于中档题.。


高一数学(必修一)《第五章 正弦函数、余弦函数的图象》练习题及答案解析-人教版班级:___________姓名:___________考号:___________一、单选题1.已知函数()sin(2)f x x ϕ=+(其中02πϕ<<)的图象经过1(,)42P π,则ϕ的值为( ) A .512π B .3πC .4π D .6π2.已知函数()cos f x x x =和()()g x f x '=,则( ). A .()g x 的图像关于点π,06⎛⎫⎪⎝⎭对称B .()g x 图像的一条对称轴是π6x =C .()g x 在5π5π,66⎛⎫- ⎪⎝⎭上递减D .()g x 在ππ,33⎛⎫- ⎪⎝⎭的值域为(0,1)3.设函数()2121log 2x a x f x x x ⎧-+<⎪⎪=⎨⎪≥⎪⎩,,的最小值为1-,则实数a 的取值范围是( ) A .12⎡⎫-+∞⎪⎢⎣⎭, B .12⎛⎫-+∞ ⎪⎝⎭, C .12⎛⎫-∞- ⎪⎝⎭, D .[)1-+∞, 4.已知函数()22πcos sin 2f x x x ⎛⎫=+- ⎪⎝⎭,将函数()f x 的图象先向右平移π12个单位长度,再向下平移1个单位长度得到函数()g x 的图象,则函数()g x 图象的对称轴方程为( ) A .()ππ+Z 12x k k =∈ B .()ππZ 6x k k =-∈ C .()ππZ 212k x k =-∈ D .()ππ+Z 212k x k =∈ 5.已知函数()f x 是定义在R 上的奇函数,当0x <时,则()()e 1xf x x =+,则下列结论中错误的是( )A .当0x >时,则()()e 1xf x x -=--B .函数()f x 有3个零点C .()0f x <的解集为()(),10,1-∞-⋃D .12,R x x ∀∈,都有()()122f x f x -<6.设集合{}{}2log 2,P x x Q y y x P =<=∈∣∣,则P Q =( ) A .{34}xx <<∣ B .{34}xx <∣ C .{04}xx <<∣ D .{05}xx <∣ 7.已知函数()f x 是定义域为(,)-∞+∞的奇函数,满足(2)(2)f x f x -=+,若(1)2f =,则(1)(2)(3)(2022)f f f f ++++=( ) A .2- B .0C .2D .48.函数()cos xf x xπ=在区间[]4,4-上的图象大致是( ) A . B .C .D .二、解答题9.已知函数2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭.(1)用五点法画出函数()f x 的大致图像,并写出()f x 的最小正周期; (2)写出函数()f x 在R x ∈上的单调递减区间; (3)将()y f x =图像上所有的点向右平移3π个单位长度,纵坐标不变,横坐标变为原来的12倍,得到()y g x =的图像,求()y g x =在区间0,2π⎡⎤⎢⎥⎣⎦上的最值.10.已知函数()22sin sin 363f x x x x πππ⎛⎫⎛⎫⎛⎫=-++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(1)求函数()f x 的单调递增区间;(2)若函数()()2g x f x a =-在区间70,12π⎡⎤⎢⎥⎣⎦上恰有3个零点()123123,,x x x x x x <<(i )求实数a 的取值范围; (ii )求()123sin 2x x x +-的值.11.某实验室某一天的温度(℃)随时间()t h 的变化近似地满足函数关系:()sin1212f t k t t ππ=-[)0,24t ∈ R k ∈ 已知早上6时,则实验室温度为9℃.(1)求函数()f t 的解析式; (2)求实验室这一天中的最大温差;(3)若要求实验室温度不高于11℃,则在哪个时间段实验室需要降温? 12.已知函数222()log log (4),()log ()f x x x g x x a =--=+. (1)求()f x 的定义域,并证明()f x 的图象关于点(2,0)对称;(2)若关于x 的方程()()f x g x =有两个不同的实数解,求实数a 的取值范围. 13.已知函数32()1f x x ax bx =+++在点(1,(1))P f 处的切线方程为420x y --=. (1)求函数()f x 的单调区间(2)若函数()()g x f x m =-有三个零点,求实数m 的取值范围.三、填空题14.函数()2log 2cos 1y x =+的定义域是______.15.已知函数()22sin sin 2f x x x =的最大值为3,则实数a 的值为______.16.若函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭在[]0,π上有且仅有3个零点和2个极小值点,则ω的取值范围为______.四、多选题17.已知函数()()()2sin 0,f x x ωϕωϕπ=+><的部分图象如图所示,则( )A .2ω=B .3πϕ=C .()f x 在区间5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递增D .若123x x π+=,则()()12f x f x =参考答案与解析1.【答案】B【分析】根据给定条件,结合特殊角的三角函数值求解作答.【详解】依题意,1()sin()cos 422f ππϕϕ=+==,而02πϕ<<,所以3πϕ=.故选:B 2.【答案】B【分析】利用导数求得()g x ,然后根据三角函数的对称性、单调性、特殊值等知识求得正确答案.【详解】()()'1sin 2sin 2g x f x x x x x ⎛⎫==-=- ⎪ ⎪⎝⎭4π2sin 3x ⎛⎫=+ ⎪⎝⎭. ππ4π3π2sin 2sin 26632g ⎛⎫⎛⎫=+==- ⎪ ⎪⎝⎭⎝⎭所以()g x 图像的一条对称轴是π6x =,B 选项正确,A 选项错误. ()g x 的最小正周期2πT =,半周期π2T= 5π5π5ππ663⎛⎫--=> ⎪⎝⎭,所以区间5π5π,66⎛⎫- ⎪⎝⎭不是()g x 的单调区间,C 选项错误. ()()4πππ02sin 2sin π2sin 0,1333g ⎛⎫==+=-= ⎪⎝⎭,D 选项错误.故选:B3.【答案】A【分析】分段讨论最小值即可.【详解】由于函数()2121log 2x a x f x x x ⎧-+<⎪⎪=⎨⎪≥⎪⎩,,的最小值为1- 当12x ≥时,则()211log 122f x f ⎛⎫≥==- ⎪⎝⎭当12x ≤时,则()112f x a >-+≥-,解得12a ≥-故选: A . 4.【答案】D【分析】整理可得()1cos2f x x =+,根据平移整理得()πcos 26g x x ⎛⎫=- ⎪⎝⎭,结合余弦函数得对称轴()ππZ 62k k x -=∈求解.【详解】()222πcos sin 2cos 1cos 22f x x x x x ⎛⎫=+-==+ ⎪⎝⎭由题意可得()cos 2cos 2ππ126g x x x ⎛⎫=-=- ⎪⎝⎭⎛⎫ ⎪⎝⎭则()ππZ 62k k x -=∈,解得()ππ+Z 212k x k =∈故选:D . 5.【答案】A【分析】由奇函数求出0x >的解析式即可判断A 选项;解方程求出零点即可判断B 选项;解分段函数不等式即可判断C 选项;求导确定单调性得出函数图象,即可判断D 选项.【详解】对于A ,已知函数()f x 是定义在R 上的奇函数,当0x >时,则0x -< ()()()e 1xf x x f x --=-+=-则()()()e 1e 1x xf x x x --=--+=-,A 错误;对于B ,易得()00f =,当0x <时,则()()e 10x f x x =+=,可得1x =-;当0x >时,则()()e 10xf x x -=-=可得1x =,则函数()f x 有3个零点,B 正确;对于C ,由()()()e 1,00,0e 1,0x x x x f x x x x -⎧+<⎪==⎨⎪->⎩,当0x <时,则由()()e 10xf x x =+<得1x <-;当0x >时,则由()()e 10xf x x -=-<得01x <<,则()0f x <的解集为()(),10,1-∞-⋃,C 正确;对于D ,当0x <时,则()()e 1x f x x =+,()()e 2xf x x '=+当2x <-时,则()0f x '<,()f x 单减,此时()0f x <;当20x -<<时,则()0f x '>,()f x 单增()10f -=,0x →时,则()1f x →;2x =-时,则()f x 有极小值()212e f -=-; 结合函数()f x 是定义在R 上的奇函数,可得()f x 的图象结合图象知,()f x 的值域为()1,1-,则12,R x x ∀∈,都有()()122f x f x -<,D 正确. 故选:A. 6.【答案】A【分析】由集合交集的定义计算即可.【详解】由2log 2x <解得04x <<,所以{|04}P x x =<<所以2(0,16)x ∈(3,5)和{|35}Q y y =<< 所以{|34}P Q x x =<<. 故选:A. 7.【答案】C【分析】结合函数的奇偶性、对称性和周期性求得正确答案. 【详解】()f x 是奇函数()()22f x f x -=+,即()f x 关于2x =对称()()()()()()42222f x f x f x f x f x +=++=-+=-=- ()()()()()()8444f x f x f x f x f x +=++=-+=--=所以()f x 是周期为8的周期函数.()()()()()()00,12,3212112f f f f f f ===+=-==()()()()4222200f f f f =+=-== ()()()()()52323112f f f f f =+=-=-=-=- ()()()()()6242422f f f f f =+=-=-=- ()()()74332f f f =+=-=- ()()800f f ==所以()()()()()()()()123456780f f f f f f f f +++++++= 由于202225286=⨯+ 所以(1)(2)(3)(2022)f f f f ++++=()()()()()()1234562f f f f f f +++++=.故选:C 8.【答案】C【分析】先判断函数奇偶性排除A ,再结合特殊值法和零点个数可选出正确答案. 【详解】易知函数cos ()xf x x π=是奇函数,图象关于原点对称,可以排除A ;在原点右侧附近,函数()f x 值大于0,排除D ;函数cos ()x f x x π=在区间[4,4]-上有零点1357,,,2222±±±±,共计8个,排除B.仅有C 符合上述要求. 故选:C.9.【答案】(1)图象见解析 T π=;(2)5,,1212k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦(3)()max 2g x = ()min 2g x =-; 【分析】(1)根据“五点法”列表,即可做出函数图象,再根据周期公式求出周期; (2)根据正弦函数的性质计算可得;(3)根据三角函数的变换规则得到()g x 的解析式,再根据x 的取值范围,求出43x π-的取值范围,再根据正弦函数的性质计算可得;(1)解:因为2n 2)3(si f x x π⎛⎫=+ ⎪⎝⎭ 列表如下:函数图象如下:函数()f x 的最小正周期22T ππ==. (2)解:令222,Z232k x k k πππππ-+≤+≤+∈解得5,Z 1212k x k k ππππ-+≤≤+∈ 所以函数的单调递减区间为5,,Z 1212k k k ππππ⎡⎤-++∈⎢⎥⎣⎦(3)解:将()y f x =图像上所有的点向右平移3π个单位长度得到2sin 22sin 2333y x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 再2sin 23y x π⎛⎫=- ⎪⎝⎭将横坐标变为原来的12倍,纵坐标不变得到()2sin 43g x x π⎛⎫=- ⎪⎝⎭因为0,2x π⎡⎤∈⎢⎥⎣⎦,所以54,333x πππ⎡⎤-∈-⎢⎥⎣⎦,所以[]sin 41,13x π⎛⎫-∈- ⎪⎝⎭,所以()[]2,2g x ∈-当432x ππ-=,即524x π=时()max 2g x =,当3432x ππ-=,即1124x π=时()min 2g x =-;10.【答案】(1)()5,1212k k k ππππ-++⎡⎤∈⎢⎥⎣⎦Z (2)(i )⎡⎤⎣⎦;(ii 【分析】(1)利用诱导公式、二倍角公式和辅助角公式可化简得到()2sin 23f x x π⎛⎫=- ⎪⎝⎭;根据正弦型函数单调性的求法可求得单调递增区间; (2)(i )令43t x π=-,将问题转化为2sin y t =与y a =在,23ππ⎡⎤-⎢⎥⎣⎦上恰有3个不同的交点,利用数形结合的方式即可求得a 的取值范围;(ii )由(i )中图像可确定233t t π+=,312t t π-=由此可得1232t t t π+-=-,整理可得123212x x x π+-=-,由两角和差正弦公式可求得sin12π-的值,即为所求结果.(1)()22sin cos 2cos 13263f x x x x ππππ⎛⎫⎫⎛⎫⎛⎫⎛⎫=--++-- ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎭2222sin cos 2sin 2233333x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=--+-=-- ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭22sin 22sin 2333x x πππ⎛⎫⎛⎫=-+=- ⎪ ⎪⎝⎭⎝⎭; ∴令()222232k x k k πππππ-+≤-≤+∈Z ,解得:()51212k x k k ππππ-+≤≤+∈Z ()f x ∴的单调递增区间为()5,1212k k k ππππ-++⎡⎤∈⎢⎥⎣⎦Z .(2)(i )由(1)得:()2sin 43g x x aπ⎛⎫=-- ⎪⎝⎭当70,12x π⎡⎤∈⎢⎥⎣⎦时,则4,233x πππ⎡⎤-∈-⎢⎥⎣⎦设43t x π=-,则()g x 在区间70,12π⎡⎤⎢⎥⎣⎦上恰有3个零点等价于2sin y t =与y a =在,23ππ⎡⎤-⎢⎥⎣⎦上恰有3个不同的交点;作出2sin y t =在,23ππ⎡⎤-⎢⎥⎣⎦上的图像如下图所示由图像可知:当0a ≤≤时,则2sin y t =与y a =恰有3个不同的交点∴实数a 的取值范围为⎡⎤⎣⎦;(ii )设2sin y t =与y a =的3个不同的交点分别为()123123,,t t t t t t << 则233t t π+= 312t t π-= ()123323232224t t t t t t t t πππ∴+-=-+-=+-=-即1232444333x x x ππππ⎛⎫⎛⎫⎛⎫-+---=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭整理可得:1238443x x x π+-=-123212x x x π∴+-=-()123sin 2sin sin sin cos cos sin 12464646x x x πππππππ⎛⎫⎛⎫∴+-=-=--=-+ ⎪ ⎪⎝⎭⎝⎭12==.11.【答案】(1)()102sin 123f t t ππ⎛⎫=-+ ⎪⎝⎭ (2)最大温差为4℃ (3)10时至18时【分析】(1)将6t =代入求出k 值即可得解.(2)在[)0,24t ∈时,则求出函数()f t 的最大值与最小值即可得解. (3)解关于t 的三角不等式()11f t >即可作答.(1)因1()sin )2sin()12212123f t k t t k t ππππ=-+=-+则当6t =时,则()2sin(6)9123f t k ππ=-⨯+=,解得10k =所以()f t 的解析式为()102sin()123f t t ππ=-+.(2)因024t ≤<,则731233t ππππ≤+<,得1sin()1123ππ-≤+≤t ,当1232t πππ+=,即2t =时,则()f t 取最小值8当31232t πππ+=,即14t =时,则()f t 取最大值12,即实验室这一天中的最高温度为12℃,最低温度8℃所以最大温差为4℃. (3)依题意,当()11f t >时,则实验室需要降温由()102sin 11123f t t ππ⎛⎫=-+> ⎪⎝⎭,得1sin 1232t ππ⎛⎫+<-⎪⎝⎭ 而当024t ≤<,即731233t ππππ≤+<时,则则有71161236t ππππ<+<,解得1018t <<所以在10时至18时实验室需要降温.12.【答案】(1)定义域为()0,4,证明见解析;(2)10a -<<.【分析】(1)根据解析式有意义可求函数的定义域,可证()()40f x f x +-=,从而得到()f x 的图象关于点(2,0)对称.(2)根据根分布可求参数的取值范围.(1)由题设可得040x x >⎧⎨-<⎩,故04x <<,故()f x 的定义域为()0,4而()()2222()4log log (4)log 4log 0f x f x x x x x +-=--+--=故()f x 的图象关于点(2,0)对称.(2)因为()()f x g x =有两个不同的实数解 故4x x a x=+-在()0,4上有两个不同的实数解 整理得到:2(3)40x a x a +--=在()0,4上有两个不同的实数解设()2(3)4h x x a x a =+--,则()()()2004030423160h h a a a >⎧⎪>⎪⎪-⎨<<⎪⎪⎪-+>⎩ 故240164(3)4030421090a a a a a a ->⎧⎪+-->⎪⎪-⎨<<⎪⎪++>⎪⎩,解得10a -<<. 13.【答案】(1)单调递减区间是11,3⎛⎫- ⎪⎝⎭,单调递增区间是1(,1),,3⎛⎫-∞-+∞ ⎪⎝⎭ (2)22,227⎛⎫ ⎪⎝⎭【分析】(1)根据题意,列出方程组求得()321f x x x x =+-+,得到()2321f x x x '=+-,进而求得函数的单调区间;(2)由题意得到()321g x x x x m =+-+-,结合条件列出不等式组,即得.(1)由题可得2()32f x x ax b '=++ 由题意得(1)22(1)324f a b f a b =++=⎧⎨=++='⎩解得1,1a b ==-所以322()1,()321f x x x x f x x x =+-+=+-'由()0f x '>得1x <-或13x > 由()0f x '<得113x -<< 所以()f x 的单调递减区间是11,3⎛⎫- ⎪⎝⎭,单调递增区间是1(,1),,3⎛⎫-∞-+∞ ⎪⎝⎭; (2)因为322()()1,()()321g x f x m x x x m g x f x x x =-=+-+='-=+-'由(1)可知,()g x 在1x =-处取得极大值,在13x =处取得极小值 ()g x 的单调递减区间是11,3⎛⎫- ⎪⎝⎭,单调递增区间是1(,1),,3⎛⎫-∞-+∞ ⎪⎝⎭ 依题意,要使()g x 有三个零点,则(1)0103g g ->⎧⎪⎨⎛⎫< ⎪⎪⎝⎭⎩ 即()1201220327g m g m ⎧-=->⎪⎨⎛⎫=-< ⎪⎪⎝⎭⎩ 解得22227m <<,经检验,(2)10,(2)110g m g m -=-<=+> 根据零点存在定理,可以确定函数有三个零点所以m 的取值范围为22,227⎛⎫ ⎪⎝⎭. 14.【答案】222,233ππk πk π⎛⎫-+ ⎪⎝⎭(k ∈Z ) 【分析】根据对数函数的性质可得2cos 10x +>,再由余弦函数的图象与性质即可求解.【详解】由题意可得2cos 10x +>,解得1cos 2x >- 作出cos y x =的图象,如下:由图象可得2222,33k x k k Z ππππ-<<+∈ 所以函数的定义域为222,233ππk πk π⎛⎫-+ ⎪⎝⎭(k ∈Z ). 故答案为: 222,233ππk πk π⎛⎫-+ ⎪⎝⎭(k ∈Z ) 15.【答案】±1【分析】先化简函数的解析式得()()21f x x ϕ++13=即得解.【详解】由题得()()22sin sin 21cos 2sin 221f x x x x x x ϕ==-++,其中tan ϕ=所以()f x 13=解得1a =±.故答案为:±1.16.【答案】1023,36⎡⎫⎪⎢⎣⎭ 【分析】找到临界位置,再根据条件建立不等式求解即可.【详解】如下图,作出简图,由题意知,[)45,x x π∈,设函数()f x 的最小正周期为T因为06x πω=-,则40077210443T x x x ππωω+=+⋅== 500223226x x T x ππωω=+=+⋅= 结合[)45,x x π∈有103ππω≥且236ππω<,解得1023,36ω⎡⎫∈⎪⎢⎣⎭.故答案为:1023,36⎡⎫⎪⎢⎣⎭17.【答案】AD 【分析】由图知22T π=即可求ω;根据()012f π-=且(0)0f >求ϕ;代入验证并结合正弦函数的单调性判断在5,1212ππ⎡⎤-⎢⎥⎣⎦上单调性;由213x x π=-代入解析式,利用诱导公式转化函数式判断()()12f x f x =是否成立. 【详解】由图知:5()212122T πππ=--=,而2T πω=,可得2ω=,A 正确; ∴()()2sin 2f x x ϕ=+,又()2sin()0126f ππϕ-=-+=且(0)2sin 0f ϕ=>,有6k πϕπ=+ k Z ∈ 又ϕπ< ∴0k =,即6π=ϕ,B 错误; 综上,()2sin 26f x x π⎛⎫=+ ⎪⎝⎭ ∴5,1212x ππ⎡⎤∈-⎢⎥⎣⎦,则22[,]633x πππ+∈-,显然()f x 在5,1212ππ⎡⎤-⎢⎥⎣⎦上不单调,C 错误; 若123x x π+=,则213x x π=-,故2115()()2sin(62)3f x f x x ππ=-=-12sin(2)56x ππ=+-112sin()()26x f x π=+= D 正确.故选:AD。

6.1 正弦函数和余弦函数的图像与性质一、复习引入1 、复习( 1 )函数的观点在某个变化过程中有两个变量x 、y ,若对于x 在某个实数会合 D 内的每一个确立的值,依据某个对应法例f, y 都有独一确立的实数值与它对应,则y 就是x 的函数,记作y f x ,x D 。
( 2 )三角函数线设随意角的极点在原点O ,始边与x 轴的非负半轴重合,终边与单位圆订交于点P( x, y),过P 作x轴的垂线,垂足为M;过点A(1,0) 作单位圆的切线,设它与角的终边(当在第一、四象限角时)或其反向延伸线(当为第二、三象限角时)订交于T .规定:当OM与x 轴同向时为正当,当OM与 x 轴反向时为负值;当MP与y 轴同向时为正当,当MP 与y 轴反向时为负值;当 AT与y 轴同向时为正当,当AT 与y 轴反向时为负值;依据上边规定,则OM x , MP y ,由正弦、余弦、正切三角比的定义有:sin y yMP ;ry1cos x xOM ;rx1tany MP ATAT ;x OM OA这几条与单位圆相关的有向线段MP ,OM , AT 叫做角的正弦线、余弦线、正切线。
二、讲解新课【问题驱动 1 】——联合我们刚学过的三角比,就以正弦(或余弦 )为例,对于每一个给定的角和它的正弦值(或余弦值 )之间能否也存在一种函数关系?若存在,请对这类函数关系下一个定义;若不存在,请说明原因.1、正弦函数、余弦函数的定义( 1)正弦函数:y sin x, x R ;( 2)余弦函数: y cos x, x R【问题驱动 2 】——怎样作出正弦函数y sin x, x R 、余弦函数 y cos x, x R 的函数图象?2 、正弦函数y sin x, x R 的图像( 1) y sin x, x0,2的图像【方案 1 】——几何描点法步骤 1 :平分、作正弦线——将单位圆平分,作三角函数线(正弦线)得三角函数值;步骤 2 :描点——平移定点,即描点x,sin x ;步骤 3 :连线——用圆滑的曲线按序连接各个点小结:几何描点法作图精准,但过程比较繁。


1.以下对正弦函数y=sin x 的图象描述不正确的是( )A .在x ∈[2k π,2k π+2π](k ∈Z )上的图象形状相同,只是位置不同B .介于直线y=1与直线y=-1之间C .关于x 轴对称D .与y 轴仅有一个交点2.用五点法作y=2sin2x 的图象时,首先应描出的五点的横坐标可以是( )A .0,2π,π,32π,2πB .0,4π,2π,34π,πC .0,π,2π,3π,4πD .0,6π,3π,2π,23π3.函数sin(2)3y x π=-在区间,2ππ⎡⎤-⎢⎥⎣⎦的简图是( )4.y =cos x ,x ∈[0,2π]的图象与直线12y =的交点的个数为( ) A .0 B .1 C .2 D .3 5.方程|x|=cos x 在(-∞,+∞)内( )A .没有根B .有且仅有一个根C .有且仅有两个根D .有无穷多个根6.要得到函数sin y x =的图象,只需将函数cos()y x π=-3的图象( ).A. 向右平移6π个单位 B. 向右平移3π个单位 C. 向左平移3π个单位D. 向左平移6π个单位7.设函数()sin f x x =,x ∈R ,对于以下三个结论:①函数()f x 的值域是[-1,1] ②当且仅当2x kx π=+(k ∈Z )时,()f x 取得最大值1 ③当且仅当2k π+π<x <2k π+32π(k ∈Z )时,()0f x <. 根据函数的图象判断其中正确结论的个数是( ) A .0 B .1 C .2 D .38.已知k <―4,则函数y=cos 2x+k (cos x ―1)的最小值是( )A .1B .―1C .2k+1D .―2k+1 9.下列函数图象相同的序号是________.①y=cos x 与y=cos (π+x); ②sin 2y x π⎛⎫=-⎪⎝⎭与sin 2y x π⎛⎫=-⎪⎝⎭; ③y=sin x 与y=sin (-x); ④y=sin (2π+x)与y=sin x .10.若2sin x +3=a ,则实数a 的取值范围是________.【要点梳理】要点一:周期函数的定义函数)(x f y =,定义域为I ,当I x ∈时,都有)()(x f T x f =+,其中T 是一个非零的常数,则)(x f y =是周期函数,T 是它的一个周期. 要点诠释:1.定义是对I 中的每一个x 值来说的,只有个别的x 值满足)()(x f T x f =+或只差个别的x 值不满足)()(x f T x f =+都不能说T 是)(x f y =的一个周期.2.对于周期函数来说,如果所有的周期中存在一个最小的正数,就称它为最小正周期,三角函数中的要点二:正弦函数、余弦函数的图象和性质要点诠释:(1)正弦函数、余弦函数的值域为[]1,1-,是指整个正弦函数、余弦函数或一个周期内的正弦曲线、余弦曲线,如果定义域不是全体实数,那么正弦函数、余弦函数的值域就可能不是[]1,1-,因而求正弦函数、余弦函数的值域时,要特别注意其定义域.(2)求正弦函数的单调区间时,易错点有二:一是单调区间容易求反,要注意增减区间的求法,如求sin()y x =-的单调递增区间时,应先将sin()y x =-变换为sin y x =-再求解,相当于求sin y x =的单调递减区间;二是根据单调性的定义,所求的单调区间必须在函数的定义域内,因此求单调区间时,必须先求定义域.要点三:正弦型函数sin()y A x ωϕ=+和余弦型函数cos()(,0)y A x A ωϕω=+>的性质. 函数sin()y A x ωϕ=+与函数cos()y A x ωϕ=+可看作是由正弦函数sin y x =,余弦函数cos y x =复合而成的复合函数,因此它们的性质可由正弦函数sin y x =,余弦函数cos y x =类似地得到: (1)定义域:R (2)值域:[],A A -(3)单调区间:求形如sin()y A x ωϕ=+与函数cos()(,0)y A x A ωϕω=+>的函数的单调区间可以ωϕ的单调递增(减)区间对应解出x ,即为所求的单调递增(减)区间.比如:由)(2222Z k k x k ∈+≤+≤-ππϕωππ解出x 的范围所得区间即为增区间,由)(23222Z k k x k ∈+≤+≤+ππϕωππ解出x 的范围,所得区间即为减区间.(4)奇偶性:正弦型函数sin()y A x ωϕ=+和余弦型函数cos()(,0)y A x A ωϕω=+>不一定具备奇偶性.对于函数sin()y A x ωϕ=+,当()k k z ϕπ=∈时为奇函数,当()2k k z πϕπ=±∈时为偶函数;对于函数cos()y A x ωϕ=+,当()k k z ϕπ=∈时为偶函数,当()2k k z πϕπ=±∈时为奇函数.要点诠释:判断函数sin()y A x ωϕ=+,cos()y A x ωϕ=+的奇偶性除利用定义和有关结论外,也可以通过图象直观判断,但不能忽视“定义域关于原点对称”这一前提条件.(5)周期:函数sin()y A x ωϕ=+及函数cos()y A x ωϕ=+的周期与解析式中自变量x 的系数有关,其周期为2T πω=.(6)对称轴和对称中心与正弦函数sin y x =比较可知,当()2x k k z πωϕπ+=±∈时,函数sin()y A x ωϕ=+取得最大值(或最小值),因此函数sin()y A x ωϕ=+的对称轴由()2x k k z πωϕπ+=±∈解出,其对称中心的横坐标()x k k z ωϕπ+=∈,即对称中心为,0()k k z πϕω-⎛⎫∈⎪⎝⎭.同理,cos()y A x ωϕ=+的对称轴由()x k k z ωϕπ+=∈解出,对称中心的横坐标由()2x k k z πωϕπ+=±∈解出.要点诠释:若x R ∉,则函数sin()y A x ωϕ=+和函数cos()y A x ωϕ=+不一定有对称轴和对称中心.【典型例题】类型一:正弦函数、余弦函数的定义域与值域例1.求函数y =举一反三:【变式1】求函数lg(2sin 1)y x =-的定义域例2.求下列函数的值域: (1)y=3―2sin x (2)2sin 23y x π⎛⎫=+ ⎪⎝⎭,,66x ππ⎡⎤∈-⎢⎥⎣⎦; (3)cos 2cos 1x y x -=-.举一反三:【变式1】 求y=cos 2x+4sin x ―2的值域.类型二:正弦函数、余弦函数的单调性例3.(浙江温州期末)设函数()sin(2)3f x a x b π=++(1)若a >0,求f (x )的单调递增区间; (2)当[0,]4x π∈时,f (x )的值域为[1,3],求a ,b 的值.举一反三:【变式1】(河南期中)已知函数1sin()32y x π=- (1)求该函数的周期,并求函数在区间[0,π]上的值域; (2)求该函数在[-2π,2π]上的单调增区间.类型三:正弦函数、余弦函数的奇偶性 例4.判断下列函数的奇偶性:(1)5())2f x x π=+;(2)()f x =;举一反三:【变式】关于x 的函数)(x f =sin(x+ϕ)有以下命题: ①对任意的ϕ,)(x f 都是非奇非偶函数; ②不存在ϕ,使)(x f 既是奇函数,又是偶函数; ③存在ϕ,使)(x f 是奇函数; ④对任意的ϕ,)(x f 都不是偶函数.其中一个假命题的序号是_____.因为当ϕ=_____时,该命题的结论不成立.类型四:正弦函数、余弦函数的对称性例5.(湖南益阳月考)已知函数()2sin(2)4f x x π=-.(1)求函数的最值及相应的x 值集合; (2)求函数的单调区间;(3)求函数f (x )的图象的对称轴与对称中心.举一反三:【变式1】指出下列函数的对称轴与对称中心 (1)sin()4y x =+π;(2)cos(2)3y x =-π.类型五:正弦函数、余弦函数的周期 例6.求下列函数的周期: (1)sin 3y x π⎛⎫=+⎪⎝⎭; (2)cos 2y x =;(3)3sin 23x y π⎛⎫=+⎪⎝⎭; (4)112sin cos 2326y x x ππ⎛⎫⎛⎫=+-- ⎪ ⎪⎝⎭⎝⎭举一反三:【变式1】判断下列函数是否是周期函数.若是周期函数,求其最小正周期. (1)|sin |y x =; (2)sin ||y x =; (3)sin(2)3y x =-π.类型六:正弦函数、余弦函数性质的综合应用 例7.已知函数12()log |sin |f x x =.(1)求其定义域和值域; (2)判断奇偶性;(3)判断周期性,若是周期函数,求周期; (4)写出单调区间.举一反三: 【变式】已知函数11cos |cos |22y x x =+. (1)画出函数的简图;(2)这个函数是周期函数吗?如果是,求出它的最小正周期; (3)指出这个函数的单调增区间.【巩固练习】1.下列函数是以π为周期的函数的是( )A .1sin2y x = B .y=cos2x C .y=1+sin3x D .y=cos3x 2.下列函数中是偶函数的是( )A .y=sin2xB .y=-sin xC .y=sin |x|D .y=sin x+1 3.已知函数()sin(2)f x x ϕ=+的图象关于直线8x π=对称,则ϕ可能是( )A .2π B .4π- C .4πD .34π4.设函数()sin 22f x x π⎛⎫=-⎪⎝⎭,x ∈R ,则()f x 是( ) A .最小正周期为π的奇函数 B .最小正周期为π的偶函数 C .最小正周期为2π的奇函数 D .最小正周期为2π的偶函数 5.下列区间中,使函数y=sin x 为增函数的是( )A .[0,π]B .3,22ππ⎡⎤⎢⎥⎣⎦ C .,22ππ⎡⎤-⎢⎥⎣⎦D .[π,2π] 6.为得到函数sin(3)3y x =-π的图象,可以将函数sin3y x =的图象( ).A . 向左平移π个单位 B . 向右平移π个单位C . 向左平移9π个单位D . 向右平移9π个单位 7.已知a ∈R ,函数()sin ||f x x a =-,x ∈R ,为奇函数,则a 的值为( )A .0B .1C .-1D .±18.(广东揭阳月考)函数y =2sin x 在区间4[,)63ππ的值域是( )A .1[)2B .(2]C .1[2D .[2) 9.函数()cos 6f x x πω⎛⎫=- ⎪⎝⎭的最小正周期为5π,其中0ω>,则ω=________.10.(湖南娄底期末)函数y =________. 11.(黑龙江期末)已知函数cos(2)3,[0,]32y a x x ππ=++∈的最大值为4,则实数a 的值为________.12.(宁夏金凤区月考)求函数y =13.求函数2cos sin y x x =-,[]0,x π∈上的值域.14.(湖南株洲月考)已知定义在[,]62x ππ∈-上的函数()sin(2)f x x π=-. (1)求()f x 的单调递增区间;(2)若方程()f x a =只有一个解,求实数a 的取值范围.15.设关于x 的函数22cos 2cos (21)y x a x a =--+的最小值为()f a ,试确定满足1()2f a =的a 的值,并对此时的a 值求y 的最大值.。

第3课时 正弦函数、余弦函数的单调性与最值教材要点要点 正、余弦函数的图象与性质正弦函数余弦函数图象值域________________单调性在________________(k ∈Z )上递增,在________________(k ∈Z )上递减在________________(k ∈Z )上递增,在________________(k ∈Z )上递减最值x =________(k ∈Z )时,y max =1;x =________(k ∈Z )时,y min =-1x =________(k ∈Z )时,y max =1;x =________(k ∈Z )时,y min =-1状元随笔 (1)正、余弦函数的单调性:①求解或判断正弦函数、余弦函数的单调区间(或单调性)是求与之相关的复合函数值域(最值)关键的一步;②单调区间要在定义域内求解;③确定含有正弦函数或余弦函数的复合函数的单调性时,要注意用复合函数法来判断.(2)正、余弦函数的最值①明确正、余弦函数的有界性,即|sin x|≤1, |cos x|≤1;②对有些函数,其最值不一定就是1或-1,要依赖函数的定义域来决定;③形如y =A sin (ωx +φ)(A >0,ω>0)的函数求最值时,通常利用“整体代换”,即令ωx +φ=z ,将函数转化为y =A sin z 的形式求最值.基础自测1.思考辨析(正确的画“√”,错误的画“×”)(1)在区间[0,3π]上,函数y =cos x 仅在x =0时取得最大值1.( )(2)正弦函数在第一象限是增函数.( )(3)存在实数x,使得cos x=√2.( )(4)余弦函数y=cos x在[0,π]上是减函数.( )2.下列函数中,既为偶函数又在(0,π)上单调递增的是( ) A.y=cos|x| B.y=cos|-x|C.y=sin (x-π2) D.y=-sinx23.函数y=1-2cos π2x的最小值,最大值分别是( )A.-1,3B.-1,1 C.0,3D.0,14.比较大小:sin 3π5________cosπ5.题型1 正弦、余弦函数的单调性例1 求函数y=√2sin (π4−2x)的单调区间.方法归纳求与正、余弦函数有关的单调区间的策略(1)结合正、余弦函数的图象,熟记它们的单调区间.(2)在求形如y=A sin (ωx+φ)(A>0,ω>0)的函数的单调区间时,应采用“换元法”整体代换,将“ωx+φ”看作一个整体“z”,即通过求y=A sin z的单调区间而求出原函数的单调区间.求形如y=A cos (ωx+φ)(A>0,ω>0)的函数的单调区间同上.(3)①ω<0时,一般用诱导公式转化为-ω>0后求解;②若A<0,则单调性相反.跟踪训练1 (1)函数f(x)=2sin (x-〖(π)/(3)〗),x∈[-π,0]的单调递增区间是( )A.B.C.D.(2)函数y=cosπx的单调减区间为________.题型2 单调性在三角函数中的应用角度1 比较大小例2 比较下列各组数的大小.(1)sin 21π5与sin42π5.(2)cos 17π8与cos37π9方法归纳比较三角函数值大小的方法(1)利用诱导公式转化为求锐角三角函数值.(2)不同名的函数化为同名函数.(3)自变量不在同一单调区间化至同一单调区间.角度2 利用正弦、余弦函数的单调性求参数例3 已知ω>0,函数f(x)=sin (ωx+π4)在(π2,π)上单调递减,则ω的取值范围是( )A.B.C.D.(0,2)方法归纳对于已知形如y=A sin (ωx+φ)或y=A cos (ωx+φ)(A>0,ω>0)的函数的单调区间的某一部分确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子区间;其次,要确定已知函数的单调区间,从而利用它们之间的关系求解.跟踪训练2 (1)sin1,sin2,sin3的大小关系是( )A.sin1<sin2<sin3B.sin3<sin2<sin1C.sin2<sin3<sin1D.sin3<sin1<sin2(2)若函数f(x)=cos2ωx(ω>0)在区间上为减函数,在区间上为增函数,则ω等于( )A.3B.2C.32D.23 三角函数的值域(或最值)问题角度1 正弦、余弦函数的值域(或最值)问题例4 求函数y=2sin (2x−π3),x∈[π3,3π4]的值域方法归纳形如y=A sin (ωx+φ)或y=A cos (ωx+φ)的三角函数值域(或最值)问题,要注意x的取值范围.一般情况下先利用x的取值范围,求出ωx+φ的范围,再求三角函数的值域(或最值).角度2 形如y=A sin2x+B sin x+C或y=A cos2x+B cos x+C型的最值(或值域)问题例5 求函数y=cos2x-sin x,x∈[−π3,π6]的最大值和最小值及相应的x值.方法归纳求形如y=A sin2x+B sin x+C,A≠0,x∈R的函数的值域或最值时,可以通过换元,令t=sin x,将原函数转化为关于t的二次函数,利用配方法求值域或最值,求解过程中要注意正弦函数的有界性(有时也用t来替换cos x).跟踪训练3 (1)函数y=2cos(2x+π6)-1的最小值是________,此时x=________.(2)函数y=y=2sin2x+2sin x-12,x∈[π6,5π6]的值域是________.易错辨析 忽视参数的分类致误例6 已知函数y=2a sin (2x−π3)+b的定义域为[0,π2],函数的最大值为1,最小值为-5,求a和b的值.解析:∵0≤x≤π2,∴-π3≤2x-π3≤2π3.∴-√32≤sin(2x−π3)≤1.若a>0,则{2a+b=1,−√3a+b=−5,解得{a=12−6√3,b=−23+12√3.若a<0,则{2a+b=−5,−√3a+b=1,解得{a=−12+6√3,b=19−12√3.易错警示易错原因纠错心得只考虑a>0的情况,漏掉了a<0的情况,导致丢解.形如y=A sin (ωx+φ)+B或y=A cos (ωx +φ)+B的函数,其最值与参数A的正负有关,因此在解决这类问题时,要注意对A分A>0和A<0两种情况进行分类讨论.课堂十分钟1.下列不等式中成立的是( ) A.sin (−π8)>sin (−π10)B.sin 3>sin 2C.sin 75π>sin (−25π)D.sin 2>cos 12.函数y=sin (−2x+π3)在区间[0,π]上的单调递增区间为( ) A.[5π12,11π12]B.[0,5π12]C.[π6,2π3]D.[2π3,π]3.已知函数f(x)=2sin (2x+π6)-1(x∈R),则f(x)在区间[0,π2]上的最大值与最小值分别是( )A.1,-2B.2,-1C.1,-1D.2,-24.已知函数f(x)=sinωx(ω>0),若f(x)在[0,π2]上单调递增,则实数ω的取值范围是________.5.求函数y=cos2x-4cos x+1,x∈[π3,2π3]的值域.第3课时 正弦函数、余弦函数的单调性与最值新知初探·课前预习要点[-1,1] [-1,1] [2kπ−π2,2kπ+π2][2kπ+π2,2kπ+3π2] [2kπ-π,2kπ] [2kπ,2kπ+π] 2kπ+π2 2kπ-π2 2kπ 2kπ+π[基础自测]1.答案:(1)× (2)× (3)× (4)√2.解析:y=cos |x|在(0,π2)上是减函数,排除A;y=cos |-x|=cos |x|,排除B;y=sin (x−π2)=-sin (π2−x)=-cos x是偶函数,且在(0,π)上单调递增,符合题意;y=-sin x2在(0,π)上是单调递减的,排除D.故选C.答案:C3.解析:∵-1≤cos π2x≤1,∴-1≤y≤3.故选A.答案:A 4.解析:sin 3π5=sin (π2+π10)=cos π10.∵0<π10<π5<π,y =cos x 在[0,π]上递减,∴cosπ10>cos π5,即sin 3π5>cos π5.答案:>题型探究·课堂解透例1 解析:∵y =√2sin (π4−2x )=-√2sin (2x−π4),∴由π2+2k π≤2x -π4≤3π2+2k π(k ∈Z ),得3π8+k π≤x ≤7π8+k π,k ∈Z .所以函数y =√2sin (π4−2x )的单调增区间为[kπ+3π8,kπ+7π8](k ∈Z ),由2k π-π2≤2x -π4≤π2+2k π,(k ∈Z ),得k π-π8≤x ≤k π+3π8(k ∈Z ).所以函数y =√2sin(π4−2x )的单调减区间为[kπ−π8,kπ+3π8](k ∈Z ).跟踪训练1 解析:(1)令2k π-π2≤x -π3≤2k π+π2,k ∈Z ,解得2k π-π6≤x ≤2k π+5π6,k ∈Z ,又∵-π≤x ≤0,∴-π6≤x ≤0.故选D.(2)由2k π≤πx ≤π+2k π,k ∈Z 得2k ≤x ≤1+2k ,k ∈Z ,即函数y =cos πx 的单调减区间为[2k ,2k +1](k ∈Z ).答案:(1)D (2)[2k ,2k +1](k ∈Z )例2 解析:(1)∵sin 21π5=sin (4π+π5)=sin π5,sin42π5=sin (8π+2π5)=sin 2π5,又∵y =sin x 在[0,π2]上单调递增,且0<π5<2π5<π2,∴sin π5<sin2π5,∴sin 21π5<sin 42π5.(2)∵cos 17π8=cos (2π+π8)=cos π8,cos37π9=cos (4π+π9)=cos π9.又∵y =cos x 在[0,π]上单调递减,∴cos π9>cos π8,∴cos37π9>cos 17π8.例3 解析:方法一 由π2<x <π,ω>0,得ωπ2+π4<ωx +π4<ωπ+π4.又因为y =sin x 在(π2,3π2)上单调递减,所以{ωπ2+π4≥π2,ωπ+π4≤3π2.解得12≤ω≤54,故选A.方法二 由π2+2k π≤ωx +π4≤3π2+2k π,k ∈Z ,ω>0,得π4ω+2kπω≤x ≤5π4ω+2kπω,k ∈Z .因此函数f (x )的单调递减区间为[π4ω+2kπω,5π4ω+2kπω],k ∈Z .由题意知(π2,π) [π4ω,5π4ω],所以{π2≥π4ω,π≤5π4ω.解得12≤ω≤54,故选A.答案:A跟踪训练2 解析:(1)sin 2=sin (π-2),sin 3=sin (π-3).∵0<π-3<1<π-2<π2,y=sin x在[0,π2]上为增函数,∴sin (π-3)<sin 1<sin (π-2),故sin 3<sin1<sin 2.故选D.(2)因为y=cos x在[0,π]上为减函数,在[π,2π]上为增函数,所以当0≤2ωx≤π,即0≤x≤π2ω时,f(x)=cos 2ωx(ω>0)为减函数,当π≤2ωx≤2π,即π2ω≤x≤πω时,f(x)=cos 2ωx(ω>0)为增函数,由题意知π2ω=π3,∴ω=32.故选C.答案:(1)D (2)C例4 解析:∵x∈[π3,3π4],∴2x∈[2π3,3π2],∴(2x−π3)∈[π3,7π6],∴sin (2x−π3)∈[−12,1].∴2sin (2x−π3)∈[-1,2],故f(x)=2sin (2x−π3)在[π3,3π4]上的值域为[-1,2].例5 解析:y=cos2x-sin x=1-sin2x-sin x=-sin2x-sin x+1,令sin x=t,∵x∈[−π3,π6],∴t∈[−√32,12],∴y =-t 2-t +1=-(t +12)2+54,∴当t =-12,即x =-π6时,f (x )有最大值,f (x )max =54;当t =12,即x =π6时,f (x )有最小值,f (x )min =14.跟踪训练3 解析:(1)当2x +π6=π+2k π,k ∈Z ,x =5π12+k π,k ∈Z ,y min =-2-1=-3.(2)令t =sin x ,∵x ∈[π6,5π6],∴t ∈[12,1],∴y =2t 2+2t -12=2(t +12)2-1,∴y ∈[1,72],故函数f (x )的值域为[1,72].答案:(1)-3 5π12+k π,k ∈Z (2)[1,72][课堂十分钟]1.解析:因为sin 2=cos (π2−2)=cos (2−π2),且0<2-π2<1<π,所以cos (2−π2)>cos 1,即sin 2>cos 1.故选D.答案:D2.解析:y =sin (−2x +π3)=-sin (2x−π3),当2k π+π2≤2x -π3≤2k π+3π2,即k π+5π12≤x ≤k π+11π12时,k ∈Z ,函数单调递增,∴函数在区间[0,π]上的单调递增区间为[5π12,11π12].故选A.答案:A3.解析:∵0≤x≤π2,∴π6≤2x+π6≤7π6,∴当2x+π6=π2时,即sin (2x+π6)=1时,函数取得最大值为2-1=1,当2x+π6=7π6时,即sin (2x+π6)=-12时,函数取得最小值为(−12)×2-1=-2.故选A.答案:A4.解析:由题意知:ω×π2≤π2,即0<ω≤1.答案:(0,1]5.解析:∵x∈[π3,2π3],∴-12≤cos x≤12.∵y=cos2x-4cos x+1=(cos x-2)2-3,∴当cos x=-12时,y max=134;当cos x=12时,y min=-34,∴y=cos2x-4cos x+1的值域为[−34,134].。


一、选择题1.函数3sin()26y x ππ=+的最小正周期是 ( ) A .4π B .2π C .4 D .22.下列函数中,周期2π为的偶函数是( ) A .cos y x = B .cos 2y x = C .sin 4x D .22cos 2sin 2x x -3.若函数1cos()2y x ϕ=+是奇函数,则ϕ的一个值可以是 ( )A .π-B .2π-C .4π-D .8π- 4.给出下列四个不等式,其中正确的是( ) ○1sin1cos1>; ○2sin 2cos2<;○3sin190cos250︒<︒;○433sin(cos )sin(sin )88ππ<。
A .○1和○2 B .○1和○3 C .○1和○4 D .○3和○4 二、填空题5.函数cos(2)3y x π=-的单调递减区间是 。
6.设3()sin 1f x ax b x =++(,a b 为常数),且(5)7f -=,则(5)f -= 。
7.若函数()f x 是周期为π的偶函数,且当[0,]2x π∈时,()sin f x x =,则5()3f π的值为 。
8.若()2sin (01)f x wx w =<<在区间[0,]3π,则w = 。
三、解答题9.已知θ是三角形的一个内角,且关于x 的函数()sin()cos()f x x x θθ=++-是偶函数,求θ的值。
10.函数2cos()23x y π=-+在区间28(,]5a π上是单调函数,求实数a 的最大值。
11.已知()log cos(2)3a f x x π=-(其中0a >且1a ≠)。
(1)求()f x 的单调区间;(2)试确定()f x 的奇偶性和周期性。
参考答案一、选择题1.C2.D3.B4.C二、填空题5.2[,],63k k k Z ππππ++∈ 6.5-7.28.34三、解答题9.34θπ=10.max 223a π= 11.(1)当1a >时,函数()f x 的增区间为:(,],126k k k Z ππππ-+∈ 函数()f x 的增区间为;5[,),612k k k Z ππππ++∈ 当01a <<时,函数()f x 的增区间为:5[,),612k k k Z ππππ++∈ 函数()f x 的增区间为;(,],126k k k Z ππππ-+∈ (2)函数()f x 的定义域不关于原点对称,函数()f x 既不是奇函数,也不是偶函数。
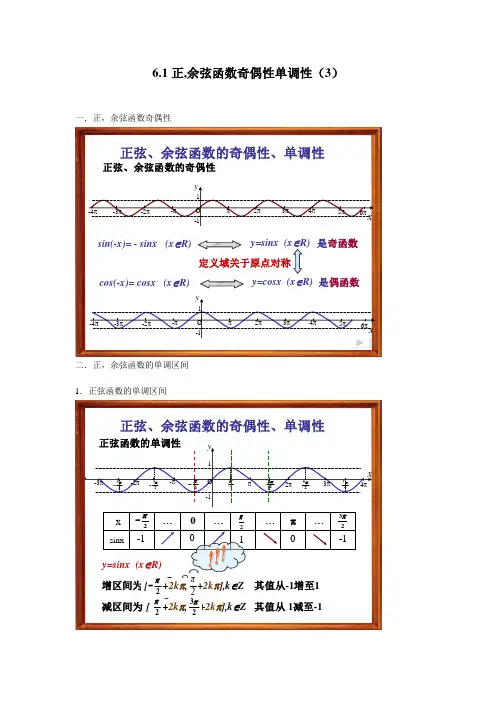
6.1正,余弦函数奇偶性单调性(3)一.正,余弦函数奇偶性正弦、余弦函数的奇偶性、单调性sin(-x)= -sinx (x ∈R)y=sinx (x ∈R)x6πyo-π-12π3π4π5π-2π-3π-4π1π是奇函数x6πo-π-12π3π4π5π-2π-3π-4π1πycos(-x)= cosx (x ∈R)y=cosx (x ∈R)是偶函数定义域关于原点对称正弦、余弦函数的奇偶性二.正,余弦函数的单调区间1.正弦函数的单调区间正弦、余弦函数的奇偶性、单调性正弦函数的单调性y=sinx (x ∈R)增区间为[ ,] 其值从-1增至12π-2πxyo-π-12π3π4π-2π-3π1π2π23π-25π27π2π-23π25π-sinxx2π-2π23π…0 ……π…-11-1减区间为[ ,] 其值从1减至-12π3π[+2k π,+2kπ],k ∈Z 2π23π[+2k π,+2k π],k ∈Z 2π-2π正弦、余弦函数的奇偶性、单调性余弦函数的单调性y=cosx (x ∈R)cosxx2π-2π-π……0 ……π-101-1增区间为其值从-1增至1[+2k π,2k π],k ∈Z π-减区间为,其值从1减至-1[2k π,2k π+ π], k ∈Zyxo-π-12π3π4π-2π-3π1π2π23π-25π27π2π-23π25π-正弦函数的对称性xyo-π-12π3π4π-2π-3π1π2π23π-25π27π2π-23π25π-)0,πk 对称中心(2ππ+=k x 对称轴:余弦函数的对称性yxo-π-12π3π4π-2π-3π1π2π23π-25π27π2π-23π25π-)0,2ππ+k 对称中心(πk x =对称轴:4.推广①)0,0)(sin(>>+=ωϕωA x A y 的单调区间Z k k x k ∈+≤+≤-,2222ππϕωππ x ⇒的范围为)sin(ϕω+=x A y 单调递增区间Z k k x k ∈+≤+≤+,23222ππϕωππx ⇒的范围为)sin(ϕω+=x A y 单调递减区间②)0,0)(cos(>>+=ωϕωA x A y 的单调区间Z k k x k ∈≤+≤-,22πϕωππ x ⇒的范围为)cos(ϕω+=x A y 单调递增区间 Z k k x k ∈+≤+≤,22ππϕωπ x ⇒的范围为)cos(ϕω+=x A y 单调递减区间二. 例题解析:例1.求下列函数的单调区间解: ()Z k ∈增区间 ()Z k ∈减区间(2))4sin(2π+-=x y 的单调递减区间解:)4sin(2π+-=x y )4sin(2)]4(sin[2ππ--=--=x xZ k k x k ∈+≤-≤-,22422πππππZ k k x k ∈+≤≤-⇒,43242ππππ单调减区间 Z k k x k ∈+≤≤+⇒,472432ππππ单调增区间例2. (1)求函数)12cos(π-=x y 的单调递增区间;解:Z k k x k ∈≤-≤-,2122ππππZ k k x k ∈+≤≤-⇒,12212112ππππ(2)求函数]0,(),62sin(2ππ-∈+=x x y 的单调递减区间.解:Z k k x k ∈+≤+≤+,2326222πππππZ k k x k ∈+≤≤+⇒,326ππππ(1) y=3sin(2x-)4π224222πππππ+≤-≤-k x k 388k x k ππππ∴-≤≤+2324222πππππ+≤-≤+k x k 3788k x k ππππ∴+≤≤+]0,(365,1πππ--≤≤--= x k ]3,65[ππ--⇒单调减区间(3))cos (sin log 31x x y -=的单调递增区间.解:0)4sin(2cos sin >-=-πx x x Z k k x k ∈+<-<+⇒,2422πππππ)4sin(2cos sin π-=-x x x 的单调递减区间Z k k x k ∈+<<+⇒,452432ππππ单调递增区间(4))(2sin 3cos 22R a a x x y ∈++=的单调递增区间. 解: )(2sin 3)22cos 1(2R a a x xy ∈+++=)(2sin 32cos 1R a a x x y ∈+++=⇒ )(1)62sin(2R a a x y ∈+++=π)](6,3[Z k k k x ∈+-∈⇒ππππ例3. 判断下列函数的奇偶性 1)x x y sin 2= 2))225sin(x y -=π3)x x x y 2cos cos sin 44+-= 4)x x y tan cot -= 5))sin 1lg()sin 1lg(x x y +--= 解:1)奇 2)偶 3)y=0既奇又偶 4)x xy 2sin 212cos =奇5)解:)(22221sin 1Z k k x k x ∈+<<-⇒<<-ππππ关于原点对称xxx x y sin 1sin 1lg )sin 1lg()sin 1lg(+-=+--=)(sin 1sin 1lg )sin 1sin 1lg(sin 1sin 1lg )sin(1)sin(1lg)(1x f xxx x x x x x x f -=+--=+-=-+=-+--=--奇函数例4. )2sin(3)(ϕ+=x x f 是偶函数的充要条件为_____________. 解:)2sin(3)(ϕ+=x x f ϕϕsin 2cos 3cos 2sin 3x x += 所以0cos =ϕZ k k ∈+=⇒,2ππϕ例5. )2cos(3)2sin(ϕϕ+++=x x y 为奇函数且在]4,0[π上是减函数的ϕ的一个解:)2c o3)2s i ϕϕ+++=x x y x x 2c )c 3(2s )s 3(ϕϕϕϕ++-= 则0cos 3sin =+ϕϕ3tan -=⇒ϕ3,32ππϕ-=⇒ ]2,0[2,2sin )sin 3(cos πϕϕ∈-=x x y 原式变为:,如果递减0sin 3cos <-⇒ϕϕ 所以32πϕ=。

完整版)正余弦函数图象与性质练习题正弦函数和余弦函数是初中数学中常见的三角函数,它们的图像和性质也是高中数学中必须掌握的内容。
一、选择题1.函数 $y=2\sin(2x+\frac{\pi}{3})$ 的图像关于点($-\frac{\pi}{6}$,0)对称。
2.函数 $y=2\sin(\frac{\pi}{6}-2x)$ 在区间$[\frac{\pi}{12},\frac{\pi}{2}]$ 上是增函数。
3.设 $a$ 为常数,且 $a>1$,$-\frac{\pi}{2}\leq x\leq 2\pi$,则函数 $f(x)=\cos 2x+2a\sin x-1$ 的最大值为 $2a+1$。
4.函数 $y=\sin(2x+\frac{5}{2}\pi)$ 的一个对称轴方程是$x=\frac{5}{4}\pi$。
5.方程 $\cos(x+\frac{5}{2}\pi)=\frac{1}{2}x$ 在区间$(0,100\pi)$ 中有 $102$ 个解。
6.函数 $y=\sin(2x+\pi)$ 是以 $\pi$ 为周期的偶函数。
7.如果函数 $y=\sin 2x+\alpha\cos 2x$ 的图像关于直线$x=-\frac{\pi}{8}$ 对称,则 $\alpha=-2$。
8.函数 $y=2\cos 2x+1$ 的最小正周期为 $\pi$。
9.已知函数 $f(x)=\sin(\pi x-\frac{\pi}{2})-1$,则命题“$f(x)$ 是周期为 $2$ 的偶函数”是正确的。
10.函数 $y=-\cos x+\frac{\cos x}{\sin x}$ 的定义域为$(2k\pi+\pi,2k\pi+\frac{3}{2}\pi]$。
11.定义在 $\mathbb{R}$ 上的函数 $f(x)$ 既是偶函数又是周期函数,且最小正周期为 $\pi$,当$x\in[\frac{\pi}{2},\pi]$ 时,$f(x)=\sin x$,则$f(\frac{5\pi}{3})=-\frac{1}{2}$。
高一数学正弦函数、余弦函数的图象和性质通用版【本讲主要内容】正弦函数、余弦函数的图象和性质【知识掌握】【知识点精析】(0, (2)7C(0, 1)( — , 0) ( n , -1) 3兀~20) (2 JI , 1)7T3兀减区间:[- + 2^ —+ 2^]伙G Z)2 2 减区间:[2k兀,兀 + 2k/rl(k G Z)最大(小)值x =—F 2上兀吋,最大值为12x = -- + 2^时,最小值为一1 (kez) 2x=2kn时,最大值为1xF+2kn时,最小值为一1 (kez)2.三角函数的周期性①周期函数的定义:一般地,对于函数/(X),若存在常数T(THO),使得当x取它定义域内的每一个值时,都有f(x + T) = f(x),则函数/(兀)就叫做周期函数,T叫做/(劝的周期。
②最小正周期:若/(力的所有周期中存在一个最小正数,则称这个最小正数为最小正周期。
③正弦函数,余弦函数都是周期函数,2k兀(k£Z且kHO)都是它们的周期,最小正周期是2 n o(注意:以后若不加说明,周期都是指函数的最小正周期)④一般地:函数y = Asin(0r + 0), xeR 及函数y = A COS(@Y +0), xeR(其中A, 3,0为常数,且AHO, 3〉0)的周期为7 =——CO3.用“五点法”作正弦函数和余弦函数的简图用儿何法做出图象比较精确,但画图较繁。
因此,在精度要求不太高时,我们常常采用“五点作图法”。
(1)正弦函数y = sinx, xw [0,2龙]的图象屮,五个关键点是:因此,在精度要求不太高时,我们常常先描出五个关键点,然后用光滑的曲线依次连接 起来,就分别得到T y=sinx, y=cosx, X e [0, 2兀]的简图,这种作图法称为“五点法”。
【解题方法指导】例1.求下列函数的定义域。
(1) y = Jcosx + J —兀2 + 7兀一 6 (2) y = lg(sinx ——)2分析:应先列出使函数有意义的几个不等式,然后利用数轴或者图象求出它们的公共 解集。
正弦函数的性质与图像、余弦函数的图像与性质和正切函数 正弦函数的性质与图像[要点]1.正弦函数的图像(1)掌握正弦函数的图像的画法;(2)会熟练运用五点法画有关正弦函数的简图. 2.对于正弦函数x y sin =要掌握: (1)定义域为R ; (2)值域[-1,1]; (3)最小正周期π2; (4)单调增区间],22,22[ππππ+-k k 单调减区间]232,22[ππππ++k k ,Z k ∈; (5)是奇函数,图像关于原点对称.同时要求会求有关正弦函数的一些简单组合的函数的定义域、值域与最值、单调性、周期与判断奇偶性问题. [随堂练习]1.sin y x =,[0,2]x π∈的图像与2y =-的交点个数为〔 〕 A .0B .1C .2D .32.()f x 为奇函数,且在[,0]2π-上为减函数,则()f x 可以为〔 〕A .()sin f x x =B .()sin f x x =-C .()1sin f x x =+D .()1sin f x x =-3.函数y =的值域是〔 〕A .1[0,]2B .C .D . 4.下列不等式正确的是〔 〕A .ππ74sin 75sin >B .9sin()sin 77ππ-> C .)6sin()75sin(ππ->-D .sin()sin 37ππ->5.函数11sin ,2y x x =-∈R 的最大值为,当取得这个最大值时自变量x 的取值的集合是.6.已知02θπ≤<,则满足1sin 2θ≤的θ的范围为__________. 7.构造一个周期为2π,最小值为32-,在[0,]2π上是减函数的奇函数()f x = __ .8.利用“五点法〞画出函数1sin 2y x =-在长度为一个周期的闭区间的简图.9.求函数2sin sin 1,[,]44y x x x ππ=-++∈-的值域.答案1.C 在同一坐标系内画出sin y x =,[0,2]x π∈的图像与2y =-的图像, 可以看出交点个数为2. 2.B 对于A ,在[,0]2π-上为增函数;C 、D 都既不是奇函数,也不是偶函数.3.D 知311sin 222x -≤-≤,又在根号下,则110sin 22x ≤-≤,则[0,2y ∈. 4.B 5243sin sin sin sin 7777ππππ=<=,92sin()sin sin()777πππ->=-,52sin()sin sin()sin 7766ππππ-=-<-=-,sin()0sin 37ππ-<<,则B 正确. 5.32{2,}2x x k k Z ππ=-∈当sin x 取到最小值1-时,y 取最大值32, 此时{2,}2x x k k Z ππ=-∈.6.5[0,][,2)66πππ⋃画出12y =与sin y x =在[0,2)x π∈上的图像,看图可得. 7.3sin 2x -可以判断()f x =3sin 2x -满足要求.8.解:列表:作图:9.解:由[,]44x ππ∈-222215sin sin 1(sin )24y x x x =-++=--+,当1sin 2x =,即6x π=时,y 取最大值,为54;当sin 2x =-,即4x π=-时,y 取最小值,为12.所以函数的值域为15[,]24.备选题1.函数412sin y x=-+-的最大值是〔 〕A .35B .25C .3D .5 1.C 12sin 3x ≤-≤,则44432sin x ≤≤-,则133y ≤≤,选C . 2.已知函数5sin ,[,]22y x x ππ=∈的图像与直线1y =围成一个封闭的平面图形,则该封闭图形的面积为〔 〕 A .2 B .4 C .2π D .π2.C 如图,由对称性知12S S =,34S S =, 则封闭图形的面积与长为2π,宽为1的矩形的面积相等,则封闭图形的面积为2π.余弦函数的图像与性质 [要点]1.余弦函数的图像(1)掌握余弦函数的图像的画法;(2)会熟练运用五点法画有关余弦函数的简图. 2.对于余弦函数x y cos =要掌握:(1)定义域为R ; (2)值域[-1,1]; (3)最小正周期π2;(4)单调增区间],2,)12[(ππk k -单调减区间])12(,2[ππ+k k Z k ∈; (5)是偶函数,图像关于y 轴对称.同时要求会求有关余弦函数的一些简单组合的函数的定义域、值域与最值、单调性、周期与判断奇偶性问题. [随堂练习]1.12cos y x =-的值域为〔 〕A .[1,3]-B .[1,3]C .[3,1]-D .[3,1]--2.函数sin()2y x π=+〔x ∈R 〕〔 〕A .是奇函数,且在[,]22ππ-上是增函数 B .是偶函数,且在[,0]π-上是减函数 C .是偶函数,且在[0,]π上是减函数D .是奇函数,且在[,]22ππ-上是减函数 3.函数cos y x =-的图像的一条对称轴方程是〔 〕A .2π-=xB .4π-=xC .8π=x D .x π=4.把函数sin y x =-的图像经过平移可以得到cos y x =的图像,这个平移可以为〔 〕A .向左平移2π个单位B .向右平移2π个单位C .向左平移π个单位D .向右平移π个单位5.函数y =的定义域为___________________.6.函数12cos y x=+的值域为_______________.7.函数x x y cos sin -+=的定义域是____________________. 8.判断下列函数的奇偶性:〔1〕()cos f x x x x =-; 〔2〕1()sin cos lg1xf x x x x-=⋅+. 9.用五点法作出函数2cos y x =-,[0,2]x π∈的图像,并说明它和函数cos y x =,[0,2]x π∈的图像的关系.答案1.A 因为cos [1,1]x ∈-,则2cos [2,2]x -∈-,则12cos [1,3]x -∈-. 2.C sin()cos 2y x x π=+=,则它是偶函数,且在[0,]π上是减函数.3.D 画出图像可知直线x π=是cos y x =-的图像的一条对称轴. 4.B ∵sin()cos 2y x x π=--=,则把函数sin y x =-的图像向右平移2π个单位 可以得到cos y x =的图像.5.3{2,}4x x k k Z ππ≠±∈ 10x +≠,那么cos 2x ≠-,而cos 2x =-在一个周期[,)ππ-内的x 值为34π±,则定义域为3{2,}4x x k k Z ππ≠±∈.6.1[,1]3 因为1cos 1x -≤≤,则12cos 3x ≤+≤,知值域为1[,1]3.7.])12(,22[πππ++k k ,Z k ∈ 可得sin 0x ≥,cos 0x ≤,由正弦线与余弦线知,22k x k πππ≤≤+且32222k x k ππππ+≤≤+,其中k Z ∈,那么两者的交集 即为定义域,为])12(,22[πππ++k k ,Z k ∈. 8.解:〔1〕()()()cos()cos ()f x x x x x x x f x -=----=-+=-, 所以()f x 是奇函数.〔2〕知函数的定义域为(1,1)-.1()1()sin()cos()lgsin cos lg 1()1x xf x x x x x x x--+-=--⋅=-⋅+--111sin cos lg()sin cos lg ()11x xx x x x f x x x---=-⋅=⋅=++,所以()f x 是偶函数.9.解:在同一坐标系中作出2cos y x =-与cos y x =的图像.可以看出,将函数cos y x =,[0,2]x π∈的图像关于x 轴对称可以得到函数cos y x =-,[0,2]x π∈的图像,再将函数cos y x =-,[0,2]x π∈ 的图像向上平移2个单位即可得到函数2cos y x =-,[0,2]x π∈的图像. 备选题1.若函数()f x 是周期为π的奇函数,且[0,]2x π∈时,()cos f x x =,则7()3f π-=______. 1.12-771()(2)()()cos 333332f f f f ππππππ-=-+=-=-=-=-.2.在△ABC 中,2C π>,若函数()y f x =在[0,1]上为单调递减函数,则下列命题正确的是〔 〕A .(cos )(cos )f A fB >B .(sin )(sin )f A f B >C .(sin )(cos )f A f B >D .(sin )(cos )f A f B < 2.C 2C π>,则2A B π+<,则022A B ππ<<-<,则0sin sin()cos 12A B B π<<-=<,则(sin )(cos )f A f B >.正切函数 [要点]1.正切函数的定义:αααcos sin tan =〔Z k k R ∈+≠∈,2,ππαα〕. 2.正切函数的图像:掌握正切函数的图像的画法.3.对于正切函数x y tan =要掌握: (1)定义域为},2,{Z k k x R x ∈+≠∈ππ;(2)值域R ;(3)周期是)0,(≠∈k Z k k π,最小正周期π; (4)在每一个开区间)2,2(ππππk k ++-)(Z k ∈是增加的Z k ∈;(5)是奇函数,图像关于原点对称.同时要求会求有关余弦函数的一些简单组合的函数的定义域、值域与最值、单调性、周期与判断奇偶性问题.4.正切函数的诱导公式,可结合正弦函数与余弦函数的诱导公式的记忆方法去记忆. [随堂练习]1.已知角α的终边经过点(1,2)P -,那么tan α等于〔 〕A .2B .2-C .12 D .12- 2.若点(tan sin ,sin )P ααα-在第三象限,则角α的终边必在( )A .第一象限B .第二象限C .第三象限D .第四象限3.已知1tan()2πα-=,则3tan()2πα+等于〔 〕 A .2 B .2-C .12 D .12-4.tan y x =图像的一个对称中心为〔 〕A .(,0)2πB .(,0)4πC .(1,0)D .(0,)π 5.00tan 300cot(405)+-=.6.比较13tan()4π-与17tan()5π-的大小为13tan()4π-17tan()5π-.7.函数y =的定义域为.8.求函数)32tan(π+=x y 的定义域和单调区间.9.求函数2tan 2tan 5y x a x =+⋅+在[,)42x ππ∈时的值域(其中a 为常数). 答案1.B 可得2tan 21y x α-===-. 2.D 知sin 0α<,且tan sin 0αα-<,则tan sin 0αα<<,则α为第四象限角.3.A 1tan()2πα-=,则1tan 2α=-,则3tan()tan()cot 22ππααα+=+=-12tan α=-=.4.A tan y x =的图像可看出,(,0)2π是tan y x =的图像的一个对称中心.5.1000000tan 300cot(405)tan(36060)cot(36045)+-=-+--0000tan(60)cot(45)tan 60cot 451=-+-=--=.6.>13tan()tan()44ππ-=-,172tan()tan()55ππ-=-,又20254πππ-<-<-<,而tan y x =在(,0)2x π∈-内递增,则2tan()tan()45ππ->-,即可得.7.{,}24x k x k k Z ππππ-<<+∈可得1tan 0x ->,观察tan y x =的图像,注意tan y x =的周期为π,则定义域为{,}24x k x k k Z ππππ-<<+∈.8.解:可得πππk x +≠+232 ,z k ∈,即ππk x 23+≠,z k ∈, 所以函数的定义域是 {2,}3x x k k z ππ≠+∈.由2232x k k πππππ-+<+<+,z k ∈, 解得52233k x k ππππ-+<<+,z k ∈, 则知函数的单调区间为5(2,2)33k k k Z ππππ-++∈,且在其上为增函数.9.解:2tan 2tan 5y x a x =+⋅+22(tan )5x a a =+-+,[,)42x ππ∈,∴tan [1,)x ∈+∞,∴当1a ≤-时,25y a ≥-+,此时tan x a =-,则值域为2[5,)a -+∞; 当1a >-时,26y a ≥+,此时tan 1x =,则值域为[26,)a ++∞.备选题1.设θ是第二象限角,则〔 〕A .tan12θ>B .tan12θ<C .sincos22θθ>D .sincos22θθ<1.A θ是第二象限角,则222k k ππθππ+<<+,k Z ∈,则422k k πθπππ+<<+.当2,k n n Z =∈时,22422n n πθπππ+<<+,则tan12θ>;当21,k n n Z =+∈时,5322422n n θππππ+<<+,则tan 12θ>.2.函数tan()4y x π=-的定义域是.2.3{,}4x x k k Z ππ≠+∈知,42x k k Z πππ-≠+∈,则3,4x k k Z ππ≠+∈.同步测试题A 组一、选择题1.函数sin y x =的图像的一条对称轴方程是〔 〕A .8x π=B .54x π=C .2x π=-D .4x π=-2.1sin 、1cos 、1tan 的大小关系为( ) A .1cos 1sin 1tan >> B .1cos 1tan 1sin >> C .1tan 1cos 1sin >> D .1sin 1cos 1tan >>3.已知函数()sin 2x f x π+=,()tan()g x x π=-,则〔 〕A .()f x 与()g x 都是奇函数B .()f x 与()g x 都是偶函数C .()f x 是奇函数,()g x 是偶函数D .()f x 是偶函数,()g x 是奇函数4.下列各式中为正值的是〔 〕A .37(tan1)cot 85ππ-B .77sin tan88ππC .cos6tan 6D .00sin105cos 2305.对于下列四个命题:①sin()sin()1810ππ->-;②2517cos()cos()44ππ->-; ③00tan138tan143>;④00tan 40sin 40>.其中正确命题的序号是〔 〕A .①③B .①④C .②③D .②④ 6.若α是第一象限角,则ααααα2cos ,2tan ,2cos ,2sin,2sin 中能确定为正值的有〔 〕A .0个B .1个C .2个D .2个以上二、填空题7.平行于x 轴的直线与tan y x =的图像的相邻两个交点之间的距离为________.8.函数|tan |tan cos |cos ||sin |sin x xx x x x y ++=的值域是________.9.设,,A B C 是ABC ∆的三个内角,有下列4个关系式:①cos()cos B C A +=;②sin()sin A B C +=;③tan()tan A B C +=;④sin sin 22A B C+=.其中不正确的是______________.三、解答题10.已知tan 2α=-.〔1〕求2sin cos sin 2cos αααα+-;〔2〕求22sin 2cos 1αα-+.11.判断以下两个命题是否正确?并加以说明.〔1〕α、β都是第一象限角,若cos cos αβ>,则sin sin αβ>; 〔2〕α、β都是第四象限角,若sin sin αβ>,则tan tan αβ>.12.已知()sin f x a x b =+,5[0,]6x π∈,它的最大值为3,最小值为1.〔1〕求()f x 的表达式;〔2〕求使()2f x =成立的x 的值; 〔3〕求()f x 取最大值时x 的值.B 组一、选择题1.设()f x 是定义域为R ,最小正周期为32π的函数,若cos ,(0),()2sin ,(0).x x f x x x ππ⎧-≤<⎪=⎨⎪≤<⎩ 则15()4f π-等于〔 〕A . 1B 2.0D .22.cos cos y x x =-的值域是〔 〕A .[1,0]-B .[0,1]C .[1,1]-D .[2,0]-3.函数tan cos y x x =的部分图像是〔 〕A .B .C .D .4.已知14tan()15a π-=,那么14sin()15π-=〔 〕A .21aa +-B .21aa + C .21||aa +D .211a+-二、填空题5.已知0000cos(720)sin(540)()sin(360)tan(270)x x f x x x --=----,写出满足1()2f x =的一个x 值为_____. 6.在(0,2)π内,使sin cos x x >成立的x 取值范围为_________________.三、解答题7.已知α为第三象限角,且3sin()cos(2)tan()2()cot sin()f παπααπααπα-⋅-⋅-+=⋅+. 〔1〕化简()f α;〔2〕若31cos()25απ-=,求()f α的值.8.设关于x 的函数22cos 2cos (21)y x a x a =--+的最小值为()f a . 〔1〕写出()f a 的表达式; 〔2〕试确定能使1()2f a =的a 值,并求出此时函数y 的最大值.答案A 组1.C 观察sin y x =的图像可以看出. 2.A tan1tan14π>=,又sin1sincoscos144ππ>=>,则1cos 1sin 1tan >>.3.D ()sin cos 2x f x x π+==,()tan()tan g x x x π=-=-,易判断()f x 是偶函数,()g x 是奇函数. 4.A 3tan tan 184ππ>=,72cot cot 055ππ=>,则37(tan 1)cot85ππ-为正值. 5.B 210182ππππ-<-<-<,则sin()sin()1810ππ->-,则①正确;画出040α=的正弦线和正切线,知④正确.6.C α是第一象限角,则2α在一或三象限,则tan 2α一定为正;2α的终边在x 轴的上方,则sin 2α一定为正.7.π相邻两个交点之间的距离就是tan y x =的图像的最小正周期π.8.{1,3}-知角x 的终边不会落在坐标轴上,分角x 的终边在第一、二、三、四象限内, y 的值分别为3、-1、-1、-1,则值域是{1,3}-.9.①③④ 知A B C π++=,则A B C π+=-,B C A π+=-.可得cos()cos B C A +=-,sin()sin A B C +=,tan()tan A B C +=-,sin cos 22A B C+=.则①③④不正确.10.解:〔1〕2sin cos 2tan 12(2)13sin 2cos tan 2224αααααα++⨯-+===----.〔2〕设角α的终边与单位圆的交点为(,)P x y ,则221x y +=,则sin y α=,cos x α=,那么22sin cos 1αα+=.222222222sin cos sin 2cos 12sin cos sin cos αααααααα--+=-=+222tan 17tan 15αα-==+. 11.解:〔1〕错误,可举例030α=,060β=,满足cos cos αβ>,但sin sin αβ<.〔2〕正确,证明如下:设12k απθ=+,k Z ∈,1(,0)2πθ∈-;22n βπθ=+,n Z ∈,2(,0)2πθ∈-.∵sin sin αβ>,∴12sin sin θθ>,而sin y x =在(,0)2x π∈-上为增函数,则2102πθθ-<<<,又tan y x =在(,0)2x π∈-上为增函数,则12tan tan θθ>,则tan tan αβ>.12.解:〔1〕知sin [0,1]x ∈,由已知可以得0a ≠. 当0a >时,max ()f x a b =+,min ()f x b =,则3a b +=,1b =,那么2,1a b ==,()2sin 1f x x =+.当0a <时,min ()f x a b =+,max ()f x b =,则1a b +=,3b =,那么2,3a b =-=,()2sin 3f x x =-+. 〔2〕若()2f x =,则有1sin 2x =,5[0,]6x π∈,则6x π=,或56x π=. 〔3〕当()2sin 1f x x =+时,由2sin 13x +=,则2x π=;当()2sin 3f x x =-+时,由2sin 33x -+=,则0x =.B 组1.B 1515333()(3)()sin 44244f f f πππππ-=-+⨯===. 2.D 可得0,cos 0,2cos ,cos 0.x y x x ≥⎧=⎨<⎩ 画出图像,则它值域为[2,0]-.3.C 当2x π=无意义,则A 、B 排除,当4x π=,y =,排除D ,知选C .4.A 知1415π-是第三象限的角,则0a >,可设其终边上一点为(1,)P a --,则r OP ==14sin()15π-=5.030-00cos()sin(180)cos sin ()sin sin()tan(90)sin cot x x x x f x x x x x x --===----,由1sin 2x -=, 知满足它的一个x 值为030-. 6.5(,)44ππ在同一坐标系内画出sin y x =和cos y x =在(0,2)π内的图像,观察图像知使sin cos x x >成立的x 取值范围为5(,)44ππ.7.解:〔1〕sin cos cot ()cos cot (sin )f ααααααα⋅⋅==-⋅-.〔2〕331cos()cos()cos()sin 2225παππααα-=-=--=-=,则1sin 5α=-,则可设α的终边上一点为(1,)y -,得222(1)5y -+=,又0y <,则y =-cos α=,则()f α=. 8.解:〔1〕2222cos 2cos (21)2(cos )2122a a y x a x a x a =--+=----,cos [1,1]x ∈-,当112a-<<,即22a -<<时,2min 212a y a =---; 当12a≥,即2a ≥时,cos 1x =时,min 14y a =-; 当12a≤-,即2a ≤-时,cos 1x =-时,min 1y =.则21,2,1()21,22,214, 2.a f a a a a a a ≤-⎧⎪⎪=----<<⎨⎪-≥⎪⎩〔2〕由1()2f a =,得1a =-, 此时2112(cos )22y x =++,当cos 1x =时,y 有最大值为5.备选题1.下列函数是奇函数的是〔 〕A .tan y x x =B .sin tan y x x =C .cos(sin )y x =D .sin(tan )y x = 1.D 对于D 中函数,()sin[tan()]sin(tan )sin(tan )()f x x x x f x -=-=-=-=-, 其定义域关于原点对称,则sin(tan )y x =是奇函数.2.若函数2(sin )1y x a =-+在sin 1x =时取最大值,在sin x a =时取得最小值, 则实数a 满足〔 〕A .01a ≤≤B .10a -≤≤C .1a ≤-D .1a ≥2.B 注意sin [1,1]x ∈-,函数2(sin )1y x a =-+的对称轴为sin x a =, 由题意观察图像,则10a -≤≤.3.函数y =__________________.3.{22,}2x k x k k Z πππ-<≤∈ 可得cos 0x ≥,tan 0x ≤,则函数的图像可得{22,}22x k x k k Z ππππ-≤≤+∈,且{22,}2x k x k k Z πππ-<≤∈,求交集可得函数y ={22,}2x k x k k Z πππ-<≤∈.4.求证:ααααααααsin tan sin tan sin tan sin tan ⋅+=-⋅. 4.证明:设角α的终边上一点为(,)P x y,则r OP ==,则 222222(tan sin )(tan sin )tan sin y y x rαααααα-+=-=-22222222222222222211()tan sin r x y y y y y y x r x r x r x rαα-=-=⋅=⋅=⋅=⋅.∴ααααααααsin tan sin tan sin tan sin tan ⋅+=-⋅.。
金牌数学高一(必修四)专题系列之 正、余弦图像与性质1.正余弦函数的图像y=sinx ,x ∈R 和y=cosx ,x ∈R 的图象,分别叫做正弦曲线和余弦曲线.★2.定义域:正弦函数、余弦函数的定义域都是实数集R [或(-∞,+∞)],分别记作: y =sin x ,x ∈R y =cos x ,x ∈R★3.值域正弦函数、余弦函数的值域都是[-1,1].其中正弦函数y =sin x ,x ∈R ①当且仅当x =2π+2k π,k ∈Z 时,取得最大值1. ②当且仅当x =-2π+2k π,k ∈Z 时,取得最小值-1. 而余弦函数y =cos x ,x ∈R①当且仅当x =2k π,k ∈Z 时,取得最大值1.②当且仅当x =(2k +1)π,k ∈Z 时,取得最小值-1.4.周期性正弦函数、余弦函数都是周期函数,2k π(k ∈Z 且k ≠0)都是它的周期,最小正周期是2π.5.奇偶性y =sin x 为奇函数,y =cos x 为偶函数;正弦曲线关于原点O 对称,余弦曲线关于y 轴对称6.单调性正弦函数在每一个闭区间[-2π+2k π,2π+2k π](k ∈Z )上都是增函数,其值从-1增大到1;在每一个闭区间[2π+2k π,23π+2k π](k ∈Z )上都是减函数,其值从1减小到-1. 余弦函数在每一个闭区间[(2k -1)π,2k π](k ∈Z )上都是增函数,其值从-1增加到1;在每一个闭区间[2k π,(2k +1)π](k ∈Z )上都是减函数,其值从1减小到-1.题型一:基础回顾例1.若 cos(75° + α)=31,其中α为第三象限角,则cos(105° - α)+ sin(α - 105°)= 。
3122-. 【解析】cos(105º - α)+ sin(α - 105º) = - cos(75º + α)- sin(α + 75º).∵ 180º<α<270º,∴ 255º<α + 75º<345º.又 cos(α + 75º)=31,∴ sin(α + 75º)= -232. ∴ 原式 =312223231-=+-.拓展变式练习1.若α满足sin 2cos 2sin 3cos αααα-=+,则sin cos αα的值等于__________。
正弦函数、余弦函数的图象[学习目标] 1.了解利用单位圆中的正弦线画正弦曲线的方法.2.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.3.理解正弦曲线与余弦曲线之间的联系.知识点一 正弦曲线正弦函数y =sin x (x ∈R )的图象叫正弦曲线.利用几何法作正弦函数y =sin x ,x ∈[0,2π]的图象的过程如下: ①作直角坐标系,并在直角坐标系y 轴的左侧画单位圆,如图所示.②把单位圆分成12等份(等份越多,画出的图象越精确).过单位圆上的各分点作x 轴的垂线,可以得到对应于0,π6,π3,π2,…,2π等角的正弦线.③找横坐标:把x 轴上从0到2π(2π≈6.28)这一段分成12等份. ④平移:把角x 的正弦线向右平移,使它的起点与x 轴上的点x 重合.⑤连线:用光滑的曲线将这些正弦线的终点依次从左到右连接起来,即得y =sin x ,x ∈[0,2π]的图象.在精度要求不太高时,y =sin x ,x ∈[0,2π]可以通过找出(0,0),(π2,1),(π,0),(3π2,-1),(2π,0)五个关键点,再用光滑曲线将它们连接起来,就可得正弦函数的简图. 思考 在所给的坐标系中如何画出y =sin x ,x ∈[0,2π]的图象?如何得到y =sin x ,x ∈R 的图象?答案 y =sin x ,x ∈[0,2π]的图象(借助五点法得)如下:只要将函数y =sin x ,x ∈[0,2π)的图象向左、向右平行移动(每次2π个单位长度),就可以得到正弦函数y =sin x ,x ∈R 的图象.知识点二 余弦曲线余弦函数y =cos x (x ∈R )的图象叫余弦曲线.根据诱导公式sin ⎝ ⎛⎭⎪⎫x +π2=cos x ,x ∈R .只需把正弦函数y =sin x ,x ∈R 的图象向左平移π2个单位长度即可得到余弦函数图象(如图).要画出y =cos x ,x ∈[0,2π]的图象,可以通过描出(0,1),⎝⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫32π,0,(2π,1)五个关键点,再用光滑曲线将它们连接起来,就可以得到余弦函数y =cos x ,x ∈[0,2π]的图象.思考 在下面所给的坐标系中如何画出y =cos x ,x ∈[0,2π]的图象?答案题型一 “五点法”作图的应用例1 利用“五点法”作出函数y =1-sin x (0≤x ≤2π)的简图. 解 (1)取值列表:x0 π2 π 3π2 2π sin x 0 1 0 -1 0 1-sin x1121(2)描点连线,如图所示:跟踪训练1 作函数y =sin x ,x ∈[0,2π]与函数y =-1+sin x ,x ∈[0,2π]的简图,并研究它们之间的关系. 解 按五个关键点列表:x0 π2 π 3π2 2π sin x 0 1 0 -1 0 -1+sin x-1-1-2-1利用正弦函数的性质描点作图:由图象可以发现,把y =sin x ,x ∈[0,2π]的图象向下平移1个单位长度即可得y =-1+sin x ,x ∈[0,2π]的图象.题型二 利用正弦、余弦函数图象求定义域 例2 求函数f (x )=lg sin x +16-x 2的定义域.解 由题意得,x 满足不等式组⎩⎪⎨⎪⎧sin x >0,16-x 2≥0,即⎩⎪⎨⎪⎧-4≤x ≤4,sin x >0,作出y =sin x 的图象,如图所示.结合图象可得定义域:x ∈[-4,-π)∪(0,π).跟踪训练2 求函数f (x )=lg cos x +25-x 2的定义域.解 由题意得,x 满足不等式组⎩⎪⎨⎪⎧cos x >025-x 2≥0,即⎩⎪⎨⎪⎧cos x >0-5≤x ≤5,作出y =cos x 的图象,如图所示.结合图象可得定义域:x ∈⎣⎢⎡⎭⎪⎫-5,-32π∪⎝⎛⎭⎪⎫-π2,π2∪⎝⎛⎦⎥⎤32π,5.题型三 利用正弦、余弦函数图象判断零点个数例3 在同一坐标系中,作函数y =sin x 和y =lg x 的图象,根据图象判断出方程sin x =lg x 的解的个数.解 建立坐标系xOy ,先用五点法画出函数y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y =sin x 的图象.描出点(1,0),(10,1)并用光滑曲线连接得到y =lg x 的图象,如图所示.由图象可知方程sin x =lg x 的解有3个.跟踪训练3 方程x 2-cos x =0的实数解的个数是. 答案 2解析 作函数y =cos x 与y =x 2的图象,如图所示, 由图象,可知原方程有两个实数解.数形结合思想在三角函数中的应用例4 函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,求k 的取值围.解 f (x )=sin x +2|sin x |=⎩⎪⎨⎪⎧3sin x ,x ∈[0,π],-sin x ,x ∈π,2π].图象如图,若使f (x )的图象与直线y =k 有且仅有两个不同的交点,根据图可得k 的取值围是(1,3).1.函数y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴 C .直线y =xD .直线x =π22.用五点法画y =sin x ,x ∈[0,2π]的图象时,下列哪个点不是关键点( ) A .(π6,12)B .(π2,1)C .(π,0)D .(2π,0)3.函数y =sin x ,x ∈[0,2π]的图象与直线y =-12的交点为A (x 1,y 1),B (x 2,y 2),则x 1+x 2=.4.利用“五点法”画出函数y =2-sin x ,x ∈[0,2π]的简图.5.已知0≤x ≤2π,试探索sin x 与cos x 的大小关系.一、选择题1.函数y =-sin x ,x ∈⎣⎢⎡⎦⎥⎤-π2,3π2的简图是( )2.在同一平面直角坐标系,函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象( ) A .重合B .形状相同,位置不同C .关于y 轴对称D .形状不同,位置不同3.方程sin x =x10的根的个数是( )A .7B .8C .9D .10 4.函数y =cos x +|cos x |,x ∈[0,2π]的大致图象为( )5.如图所示,函数y =cos x |tan x |(0≤x <3π2且x ≠π2)的图象是( )6.若函数y =2cos x (0≤x ≤2π)的图象和直线y =2围成一个封闭的平面图形,则这个封闭图形的面积是( ) A .4 B .8 C .2π D.4π 二、填空题 7.函数y =log 12sin x 的定义域是. 8.函数y =2cos x +1的定义域是. 9.函数f (x )=sin x +116-x2的定义域为.10.设0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则x 的取值围为. 三、解答题11.用“五点法”画出函数y =12+sin x ,x ∈[0,2π]的简图.12.根据y =cos x 的图象解不等式:-32≤cos x ≤12,x ∈[0,2π].13.分别作出下列函数的图象. (1)y =|sin x |,x ∈R ; (2)y =sin|x |,x ∈R .当堂检测答案1.答案 D 2.答案 A 3.答案 3π 解析 如图所示,x 1+x 2=2×3π2=3π. 4.解 (1)取值列表如下:x0 π2 π 3π2 2π sin x0 1 0 -1 0 y =2-sin x21232(2)描点连线,图象如图所示:5.解 用“五点法”作出y =sin x ,y =cos x (0≤x ≤2π)的简图.由图象可知①当x =π4或x =5π4时,sin x =cos x ;②当π4<x <5π4时,sin x >cos x ;③当0≤x <π4或5π4<x ≤2π时,sin x <cos x .课时精炼答案一、选择题 1.答案 D 2.答案 B解析 根据正弦曲线的作法可知函数y =sin x ,x ∈[0,2π]与y =sin x ,x ∈[2π,4π]的图象只是位置不同,形状相同. 3.答案 A解析 在同一坐标系画出y =x10和y =sin x 的图象如图所示:根据图象可知方程有7个根.4.答案 D 解析 由题意得y =⎩⎪⎨⎪⎧2cos x ,0≤x ≤π2或32π≤x ≤2π,0,π2<x <32π.显然只有D 合适.5.答案 C解析 当0≤x <π2时,y =cos x ·|tan x |=sin x ;当π2<x ≤π时,y =cos x ·|tan x |=-sin x ; 当π<x <3π2时,y =cos x ·|tan x |=sin x ,故其图象为C. 6.答案 D解析 作出函数y =2cos x ,x ∈[0,2π]的图象,函数y =2cos x ,x ∈[0,2π]的图象与直线y =2围成的平面图形为如图所示的阴影部分.利用图象的对称性可知该阴影部分的面积等于矩形OABC 的面积,又∵OA =2,OC =2π, ∴S 阴影部分=S 矩形OABC =2×2π=4π. 二、填空题7.答案 {x |2k π<x <2k π+π,k ∈Z }解析 由log 12sin x ≥0知0<sin x ≤1,由正弦函数图象知2k π<x <2k π+π,k ∈Z .8.答案 ⎣⎢⎡⎦⎥⎤2k π-23π,2k π+23π,k ∈Z 解析 2cos x +1≥0,cos x ≥-12,结合图象知x ∈⎣⎢⎡⎦⎥⎤2k π-23π,2k π+23π,k ∈Z .9.答案 (-4,-π]∪[0,π]解析 ⎩⎪⎨⎪⎧sin x ≥0,16-x 2>0⇒⎩⎪⎨⎪⎧2k π≤x ≤2k π+π,-4<x <4⇒-4<x ≤-π或0≤x ≤π.10.答案 ⎣⎢⎡⎦⎥⎤π4,5π4 解析 由题意知sin x -cos x ≥0,即cos x ≤sin x ,在同一坐标系画出y =sin x ,x ∈[0,2π]与y =cos x ,x ∈[0,2π]的图象,如图所示:观察图象知x ∈⎣⎢⎡⎦⎥⎤π4,5π4.三、解答题11.解 (1)取值列表如下:x0 π2 π 32π 2π sin x 0 1 0 -1 0 12+sin x 123212-1212(2)描点、连线,如图所示.12.解 函数y =cos x ,x ∈[0,2π]的图象如图所示: 根据图象可得不等式的解集为{x |π3≤x ≤5π6或7π6≤x ≤5π3}.13.解 (1)y =|sin x |=⎩⎪⎨⎪⎧ sin x 2k π≤x ≤2k π+π,-sin x 2k π+π<x ≤2k π+2π(k ∈Z ).其图象如图所示,(2)y =sin|x |=⎩⎪⎨⎪⎧ sin x x ≥0,-sin x x <0.其图象如图所示,。
正弦函数、余弦函数的图像与性质(3)
一、选择题
1.函数3sin()26
y x ππ
=+的最小正周期是 ( ) A .4π B .2π C .4 D .2 2.下列函数中,周期2
π为的偶函数是( ) A .cos y x = B .cos 2y x = C .sin 4x D .22cos 2sin 2x x -
3.若函数1cos()2y x ϕ=+是奇函数,则ϕ的一个值可以是 ( )
A .π-
B .2π
- C .4π
- D .8π
-
4.给出下列四个不等式,其中正确的是( )
○1sin1cos1>; ○2sin 2cos 2<;○3sin190cos 250︒<︒;○433sin(cos )sin(sin )88ππ<。
A .○
1和○2 B .○1和○3 C .○1和○4 D .○3和○4 二、填空题
5.函数cos(2)3y x π
=-的单调递减区间是 。
6.设3()sin 1f x ax b x =++(,a b 为常数),且(5)7f -=,则(5)f -= 。
7.若函数()f x 是周期为π的偶函数,且当[0,
]2x π∈时,()sin f x x =,则5()3f π的值为 。
8.若()2sin (01)f x wx w =<<在区间[0,
]3πw = 。
三、解答题
9.已知θ是三角形的一个内角,且关于x 的函数()sin()cos()f x x x θθ=++-是偶函数,求θ的值。
10.函数2cos()23x y π=-+在区间28(,]5a π上是单调函数,求实数a 的最大值。
11.已知()log cos(2)3a f x x π
=-(其中0a >且1a ≠)。
(1)求()f x 的单调区间;
(2)试确定()f x 的奇偶性和周期性。
参考答案
一、选择题
1.C
2.D
3.B
4.C
二、填空题
5.2[,],63
k k k Z π
πππ++∈ 6.5-
78.
34 三、解答题
9.34
θπ=
10.max 223a π= 11.(1)当1a >时,函数()f x 的增区间为:(,],126
k k k Z ππππ-+∈ 函数()f x 的增区间为;5[,),612
k k k Z ππππ++∈ 当01a <<时,函数()f x 的增区间为:5[,),612
k k k Z ππππ++∈ 函数()f x 的增区间为;(,],126k k k Z ππ
ππ-+∈ (2)函数()f x 的定义域不关于原点对称,函数()f x 既不是奇函数,也不是偶函数。
函数()f x 的最小正周期是π。